- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Объем. Цилиндр, призма презентация
Содержание
- 1. Объем. Цилиндр, призма
- 2. В цилиндрический сосуд налили 1200
- 3. В цилиндрическом сосуде уровень
- 4. В сосуд, имеющий форму правильной
- 5. В сосуд, имеющий форму
- 6. В основании прямой призмы лежит
- 7. В основании прямой призмы лежит
- 8. Объем первого цилиндра равен 12
- 9. Цилиндр и конус имеют общее основание
- 10. Во сколько раз увеличится
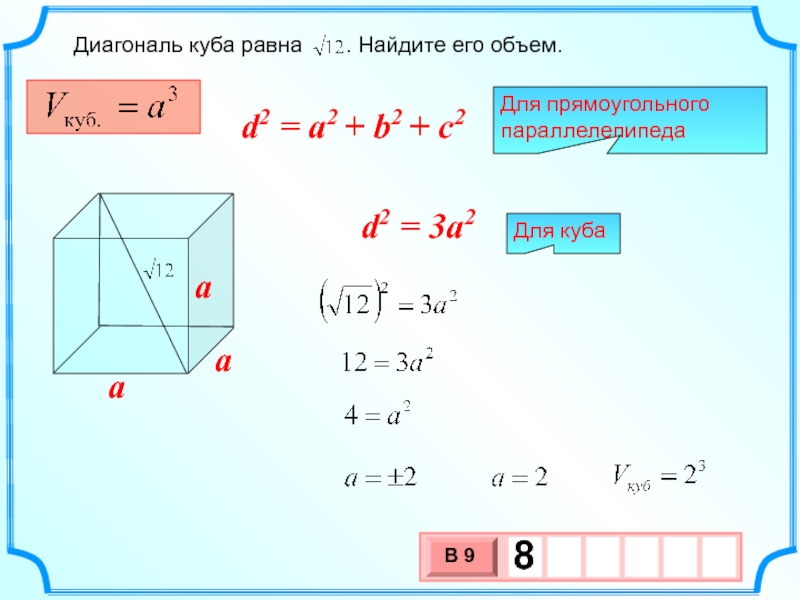
- 11. Диагональ куба равна . Найдите его объем. a a a
- 12. Объем куба равен 24 . Найдите
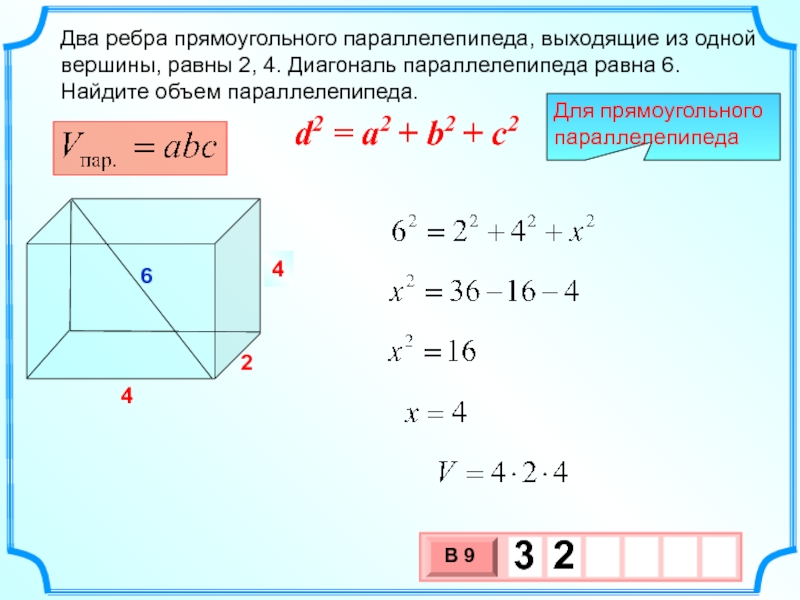
- 13. x 4 Два ребра прямоугольного параллелепипеда,
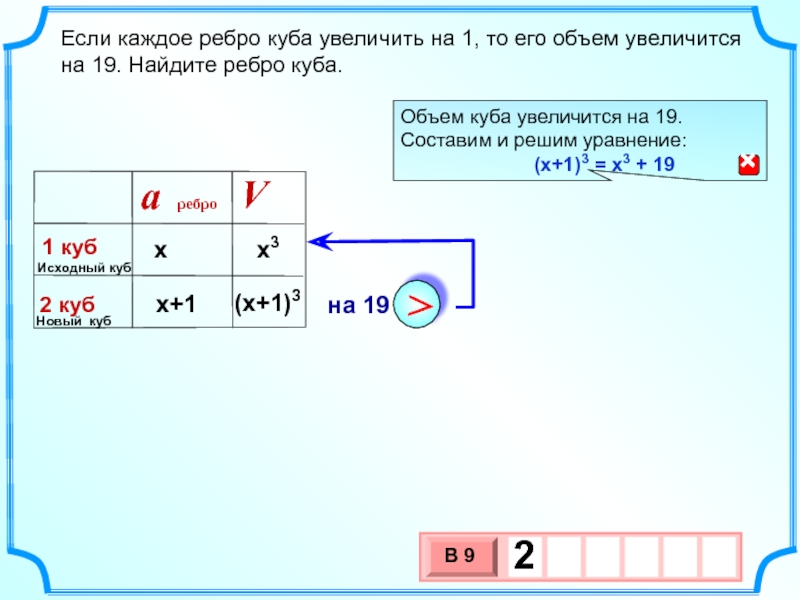
- 14. Если каждое ребро куба увеличить на 1,
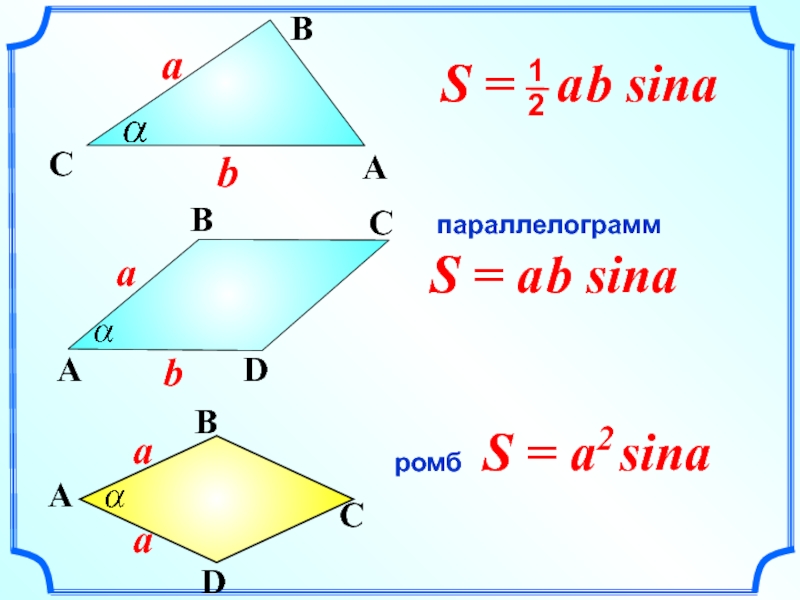
- 15. S = a2 sina параллелограмм ромб S = a b sina
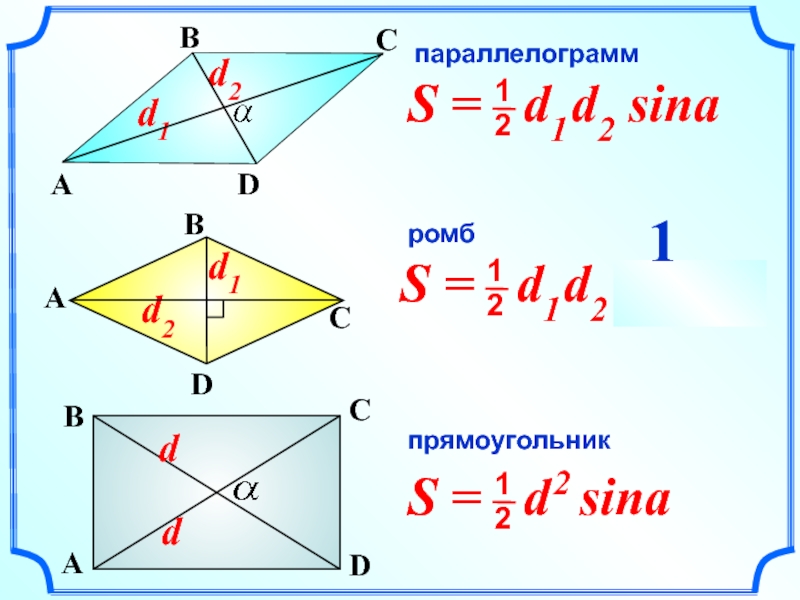
- 16. параллелограмм ромб прямоугольник 1
- 17. Найдите объем правильной шестиугольной призмы, стороны основания
- 18. Гранью параллелепипеда является ромб со
- 19. Через среднюю линию основания треугольной призмы, объем
- 20. Через среднюю линию основания треугольной призмы проведена
- 21. Объем прямоугольного параллелепипеда, описанного около сферы,
- 22. Найдите объем призмы, в основаниях которой лежат
- 23. Диагональ прямоугольного параллелепипеда равна и образует углы
- 24. Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем
Слайд 2
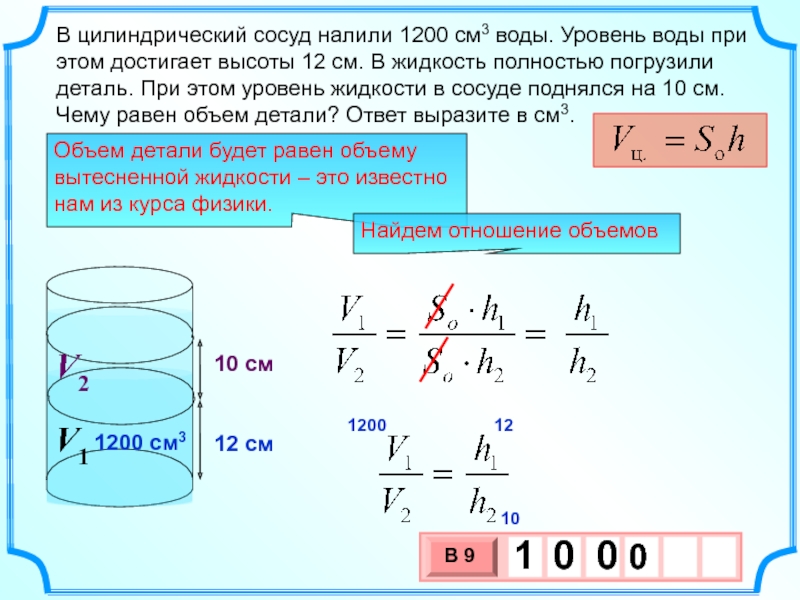
В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при этом достигает
1200
12
10
Объем детали будет равен объему вытесненной жидкости – это известно нам из курса физики.
Найдем отношение объемов
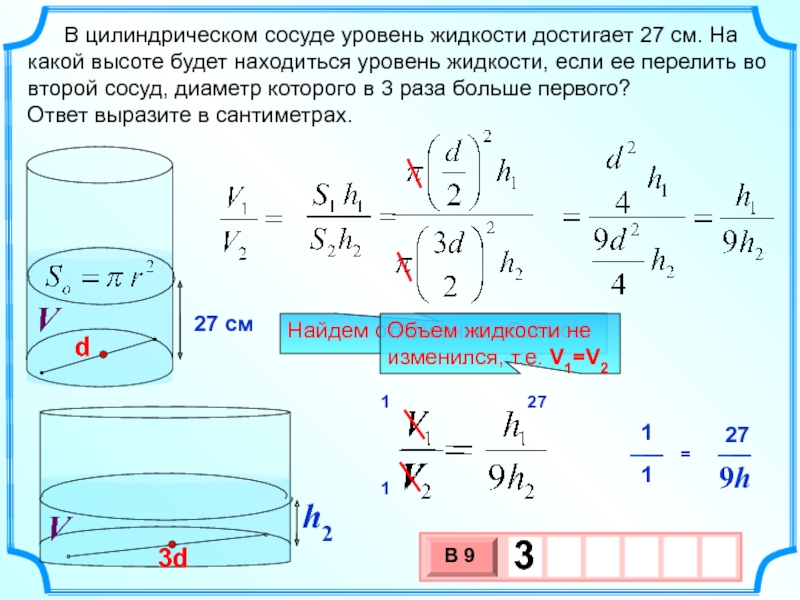
Слайд 3 В цилиндрическом сосуде уровень жидкости достигает 27 см.
Ответ выразите в сантиметрах.
27
V
d
3d
Найдем отношение объемов
Объем жидкости не изменился, т.е. V1=V2
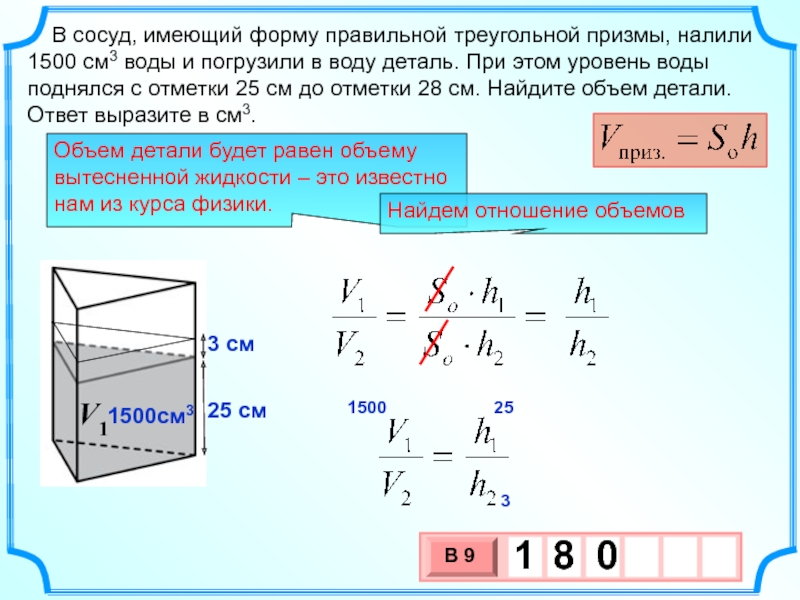
Слайд 4 В сосуд, имеющий форму правильной треугольной призмы, налили 1500 см3 воды
1500
25
3
25 см
1500см3
V1
Объем детали будет равен объему вытесненной жидкости – это известно нам из курса физики.
Найдем отношение объемов
Слайд 5
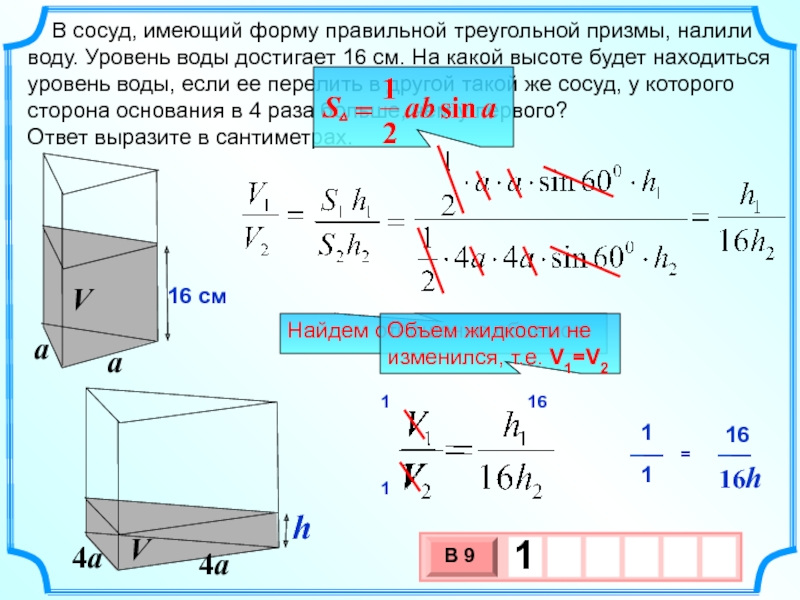
В сосуд, имеющий форму правильной треугольной призмы, налили воду.
Ответ выразите в сантиметрах.
16 см
V
h
V
a
a
4a
4a
16
Найдем отношение объемов
Объем жидкости не изменился, т.е. V1=V2
Слайд 6 В основании прямой призмы лежит прямоугольный треугольник с
катетами
5
Слайд 7 В основании прямой призмы лежит квадрат со стороной 2.
ребра равны . Найдите объем цилиндра, описанного около этой призмы.
2
2
d
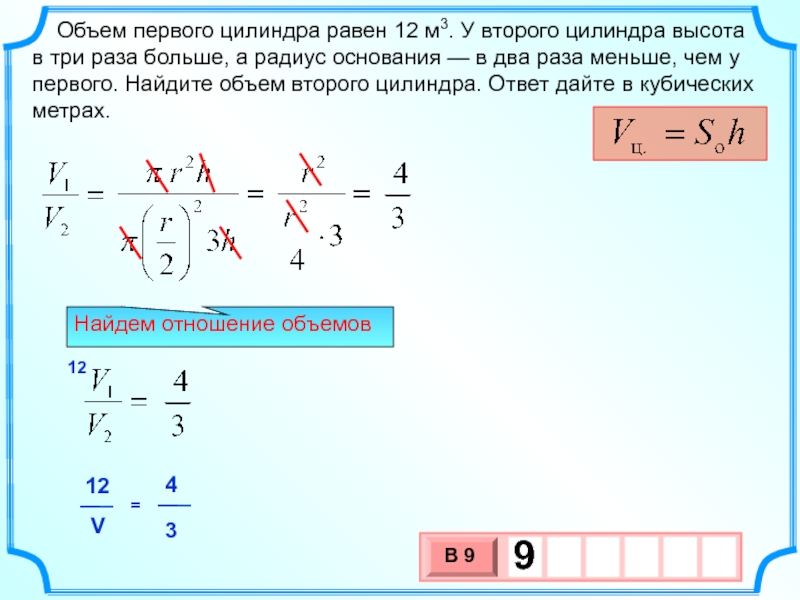
Слайд 8 Объем первого цилиндра равен 12 м3. У второго цилиндра
в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Найдем отношение объемов
12
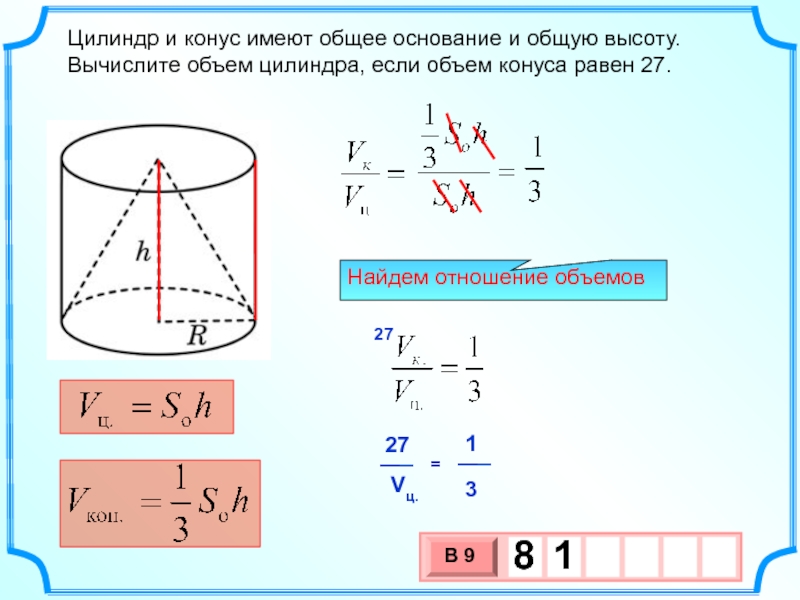
Слайд 9
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем
Найдем отношение объемов
27
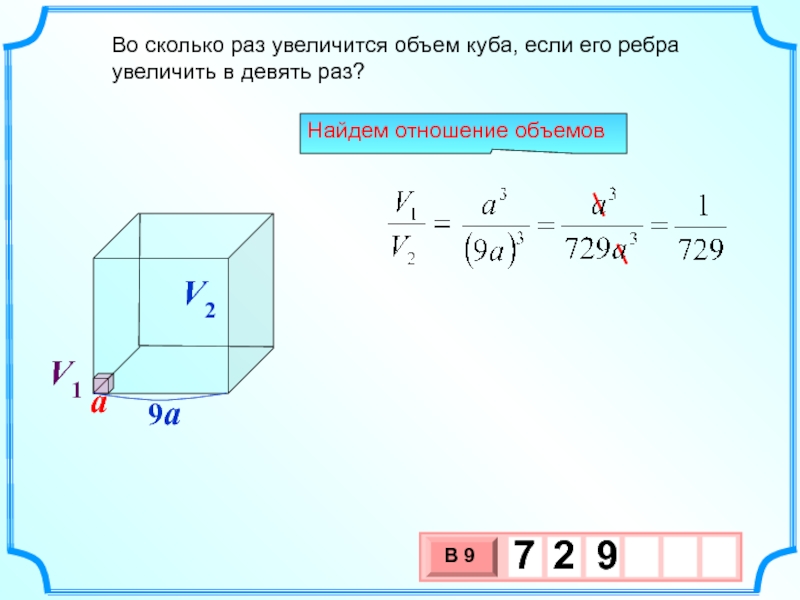
Слайд 10 Во сколько раз увеличится объем куба, если его
увеличить в девять раз?
Найдем отношение объемов
a
Слайд 13x
4
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4.
4
2
6
Слайд 14Если каждое ребро куба увеличить на 1, то его объем увеличится
х+1
(x+1)3
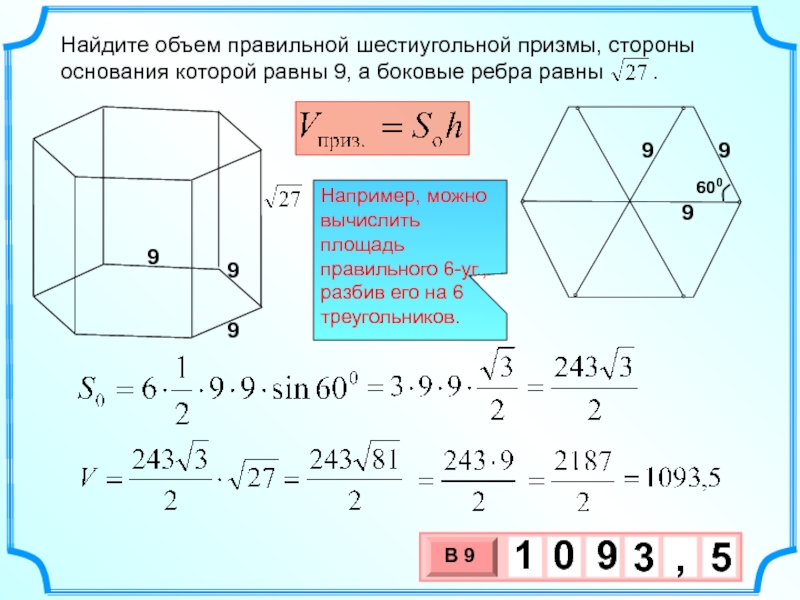
Слайд 17Найдите объем правильной шестиугольной призмы, стороны основания которой равны 9, а
9
9
9
Например, можно вычислить площадь правильного 6-уг., разбив его на 6 треугольников.
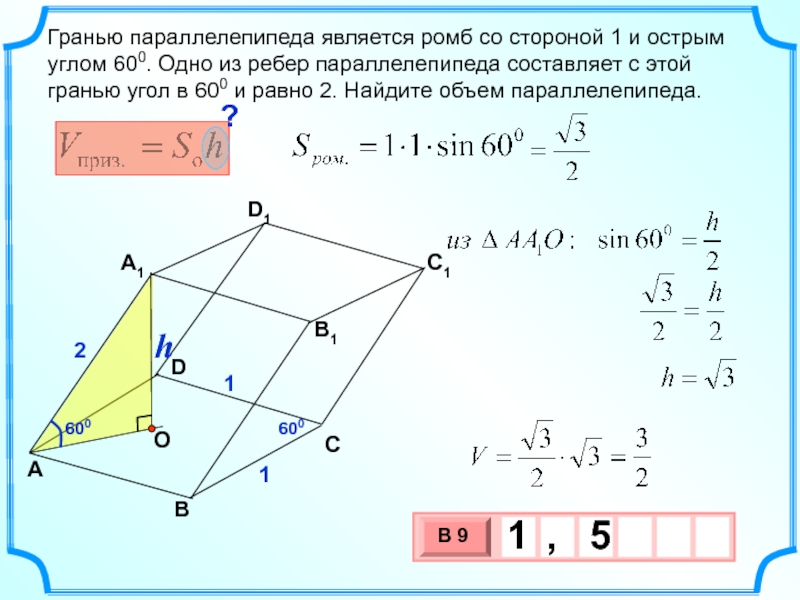
Слайд 18
Гранью параллелепипеда является ромб со стороной 1 и острым углом 600.
2
1
1
D1
C1
B1
A1
A
B
C
D
600
h
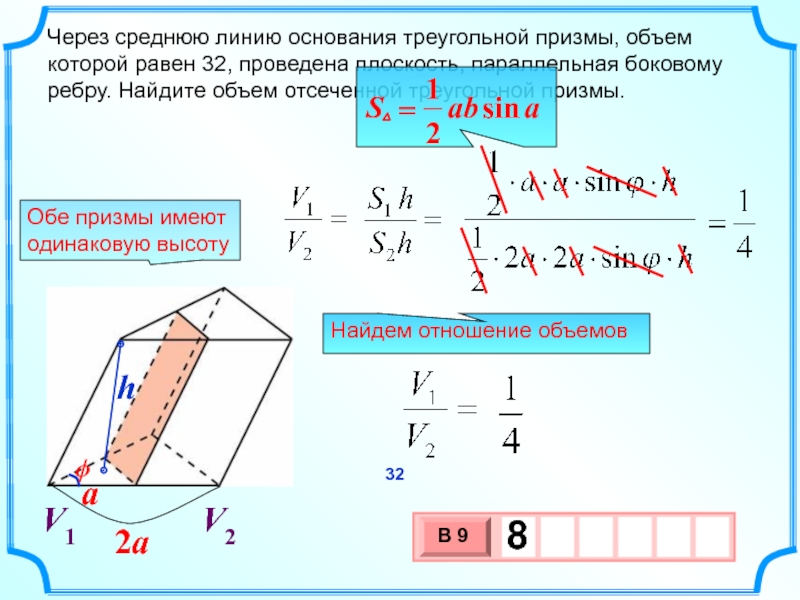
Слайд 19Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена
Найдем отношение объемов
Обе призмы имеют одинаковую высоту
32
h
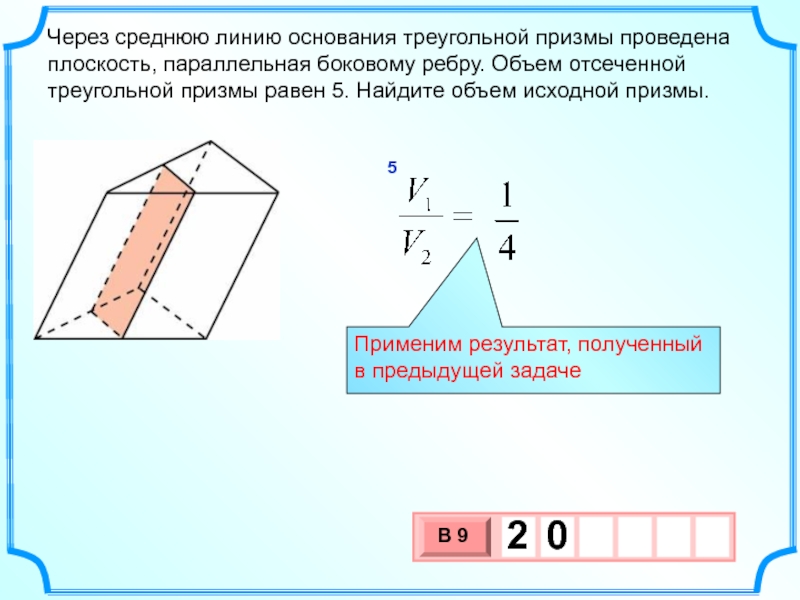
Слайд 20Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру.
5
Применим результат, полученный в предыдущей задаче
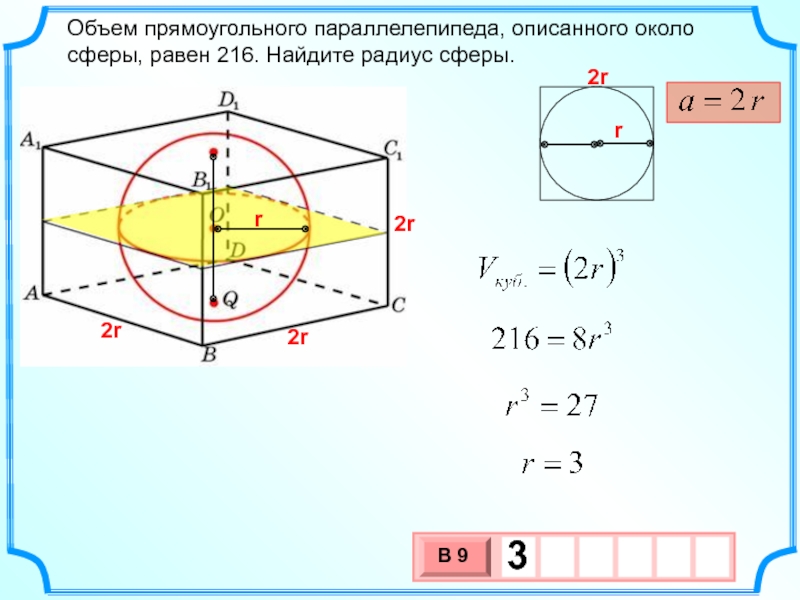
Слайд 21
Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы.
r
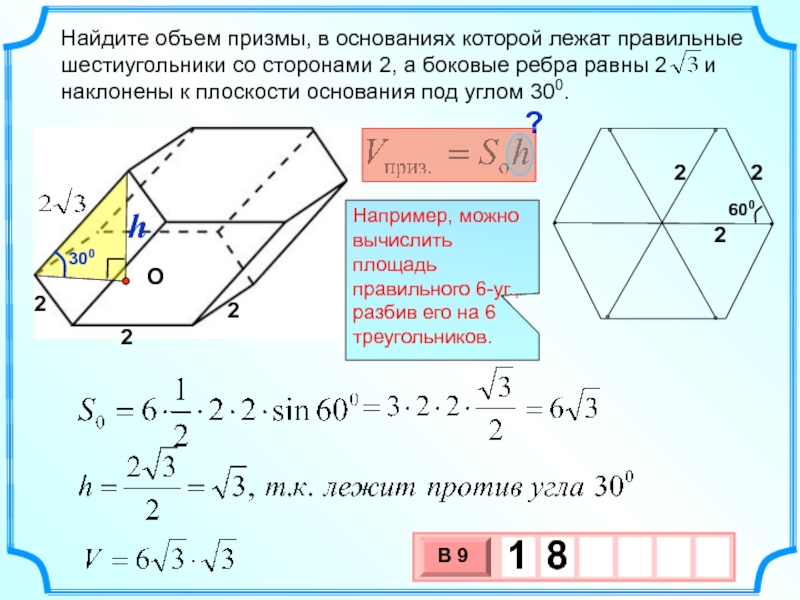
Слайд 22Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами
2
2
2
Например, можно вычислить площадь правильного 6-уг., разбив его на 6 треугольников.
Слайд 23Диагональ прямоугольного параллелепипеда равна и образует углы 300, 300 и 450
Найдем длину, ширину и высоту параллелепипеда.
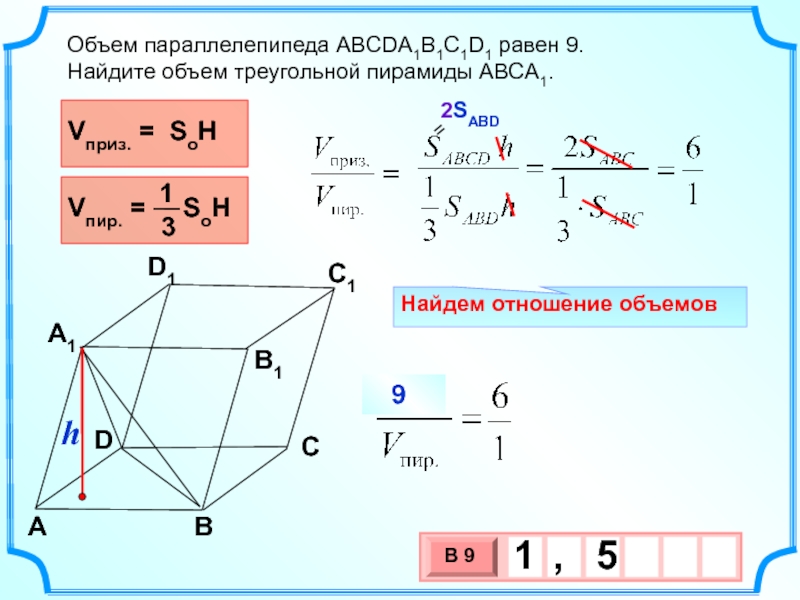
Слайд 24Объем параллелепипеда ABCDA1B1C1D1 равен 9.
Найдите объем треугольной пирамиды ABCA1.
C
A
B
A1
D1
C1
B1
D
Найдем отношение
9