- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление значений многочлена. Вычисление функций с помощью степенных рядов. Многочленные приближения презентация
Содержание
- 1. Вычисление значений многочлена. Вычисление функций с помощью степенных рядов. Многочленные приближения
- 2. Вычисление значений различных математических функций иногда представляет
- 3. Вычисление значений многочлена. Постановка задачи Пусть дан
- 4. Вычисление значений многочлена. Схема Горнера Вычисление эффективнее
- 5. Алгоритм реализации схемы Горнера В краткой форме
- 6. Разложение функций в ряд Маклорена Некоторые трансцендентные
- 7. Разложение функций в ряд Маклорена Если ряд
- 8. Рекуррентные формулы Во многих случаях вычисление членов
- 9. Разложение в ряд Маклорена некоторых элементарных функций
- 10. Разложение в ряд Маклорена некоторых элементарных функций
- 11. Вывод рекуррентной формулы для ряда ex
- 12. Приведение аргумента ex к диапазону|x| < 1
- 13. Схема алгоритма вычисления ex
- 14. Рекуррентные формулы для рядов sin(x) и cos(x)
- 15. Приведение аргумента sin(x) и cos(x) к отрезку [0; π/4]
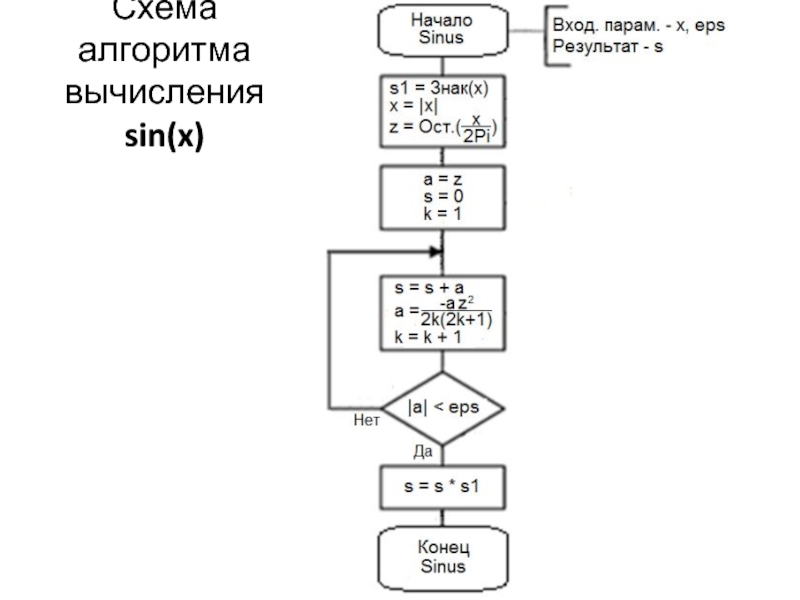
- 16. Схема алгоритма вычисления sin(x)
- 17. Рекуррентные формулы и формулы приведения для функции arctg(x) Нечетность: arctg(-x) = -arctg(x) Приведение к |x|
- 18. Рекуррентные формулы и формулы приведения для функции
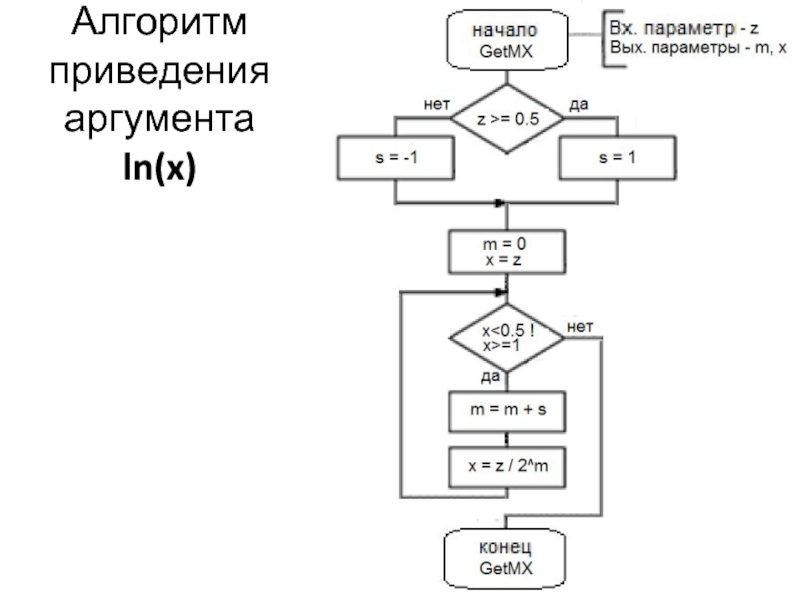
- 19. Алгоритм приведения аргумента ln(x)
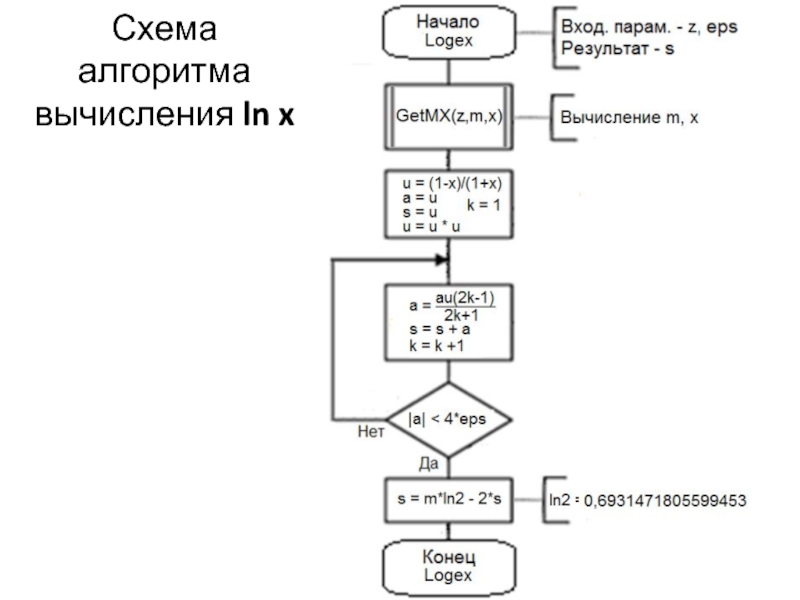
- 20. Схема алгоритма вычисления ln x
- 21. Рекуррентные формулы для рядов sinh(x) и cosh(x)
- 22. Свойства функций sinh(x) и cosh(x) Четность–нечетность sinh(-x) = -sinh(x) cosh(-x) = cosh(x)
- 23. Многочленные приближения ex и ln x ex
- 24. Многочленные приближения sin x и cos x
- 25. Многочленное приближение tg x tg x ≈
- 26. Вычисление функций методом итераций Всякую функцию y
- 27. Вычисление квадратного корня методом итераций Пусть y
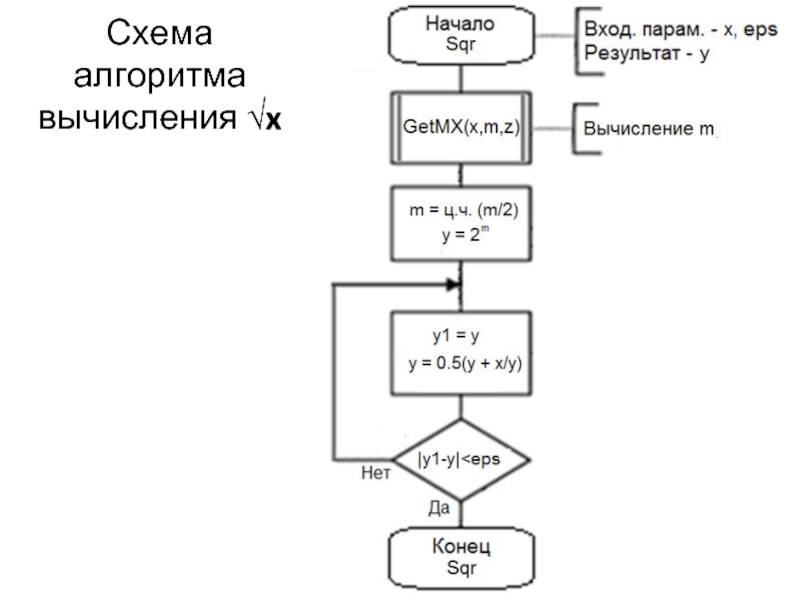
- 28. Схема алгоритма вычисления √x
- 29. Вычисление корня p–й степени методом итераций Пусть
- 30. Вычисление корня p–й степени методом итераций. Формула
Слайд 1Лекция 2
Вычисление значений многочлена. Схема Горнера
Вычисление функций с помощью степенных рядов
Многочленные
Вычисление функций методом итераций
Слайд 2Вычисление значений различных математических функций иногда представляет собой самостоятельную задачу, а
Некоторые элементарные функции (тригонометрические, логарифмические, гиперболические и ряд других) могут быть вычислены с помощью программ, входящих в состав систем программирования. Например, для вычисления функций при программировании на языке Visual Basic могут быть использованы многочисленные процедуры (методы) класса System.Math. Для использования этих функций в программе на Visual Basic необходимо в начале файла с программой поместить код Imports System.Math.
Еще большие возможности по вычислению функций дают математические пакеты прикладных программ (ППП), например, знакомые вам MathCad и MatLab. Но на практике может возникнуть необходимость вычисления функции, отсутствующей даже в ППП, а, следовательно, необходимость разработки собственной программы с использованием известных методов решения задачи. В любом случае необходимо знать методы вычисления различных функций и оценки вносимых ими погрешностей, чтобы грамотно использовать готовые программы, а при необходимости решить задачу самостоятельно.
Слайд 3Вычисление значений многочлена.
Постановка задачи
Пусть дан многочлен (полином) n-й степени:
Pn(x) = a0xn
с действительными коэффициентами
ai (i = 0, 1,…n)
и пусть требуется найти значение этого многочлена при x = u:
Pn(u) = a0un + a1un-1 + … + an-1u + an
Слайд 4Вычисление значений многочлена.
Схема Горнера
Вычисление эффективнее всего выполнять, используя лишь операции сложения
P7(u) = a0u7 + a1u6 + a2u5 + a3u4 + a4u3 + a5u2 + a6u + a7
Представим это выражение в следующем виде:
P7(u) = (((((((a0u +a1)u + a2)u + a3)u + a4)u + a5)u + a6)u + a7)
Тогда вычисление P7(u) требует выполнения следующей последовательности действий:
b0 = a0
c1 = b0u b1 = a1 + c1
c2 = b1u b2 = a2 + c2
c3 = b2u b3 = a3 + c3
c4 = b3u b4 = a4 + c4
c5 = b4u b5 = a5 + c5
c6 = b5u b6 = a6 + c6
c7 = b6u b7 = a7 + c7
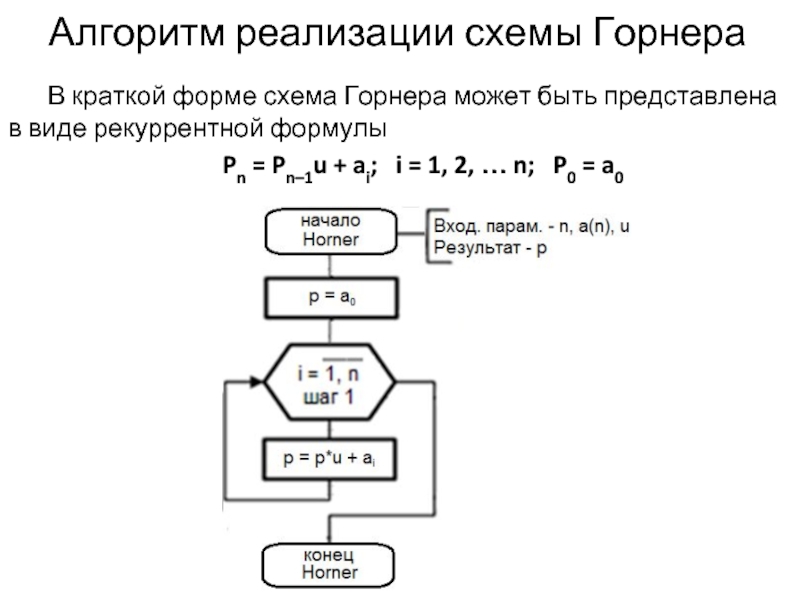
Слайд 5Алгоритм реализации схемы Горнера
В краткой форме схема Горнера может быть представлена
Pn = Pn–1u + ai; i = 1, 2, … n; P0 = a0
Слайд 6Разложение функций в ряд Маклорена
Некоторые трансцендентные (т.е. неалгебраические) функции раскладываются в
Представим этот бесконечный ряд в виде суммы
f(x) = Pn(x) + Rn(x),
где
а Rn(x) – остаточный член.
Слайд 7Разложение функций в ряд Маклорена
Если ряд Маклорена сходится, то
При вычислении функции путем разложения в ряд Маклорена надо знать радиус сходимости ряда, т.е. ограничения на величину x, и оценку величины Rn(x) для обеспечения условия |Rn(x)| < ε, где ε – заданная допустимая абсолютная погрешность.
Слайд 8Рекуррентные формулы
Во многих случаях вычисление членов ряда непосредственно по общей формуле
Записать формулу для k–го члена ряда ak.
Записать формулу для (k-1)-го члена ряда ak-1, заменив в предыдущей формуле всюду k на k-1.
Получить формулу для отношения q = ak/ak-1, произведя необходимые упрощения и сокращения.
Записать в развернутом виде полученную рекуррентную формулу в виде ak= q ∙ ak-1, значения k, при которых она работает, и значение первого члена ряда a0.
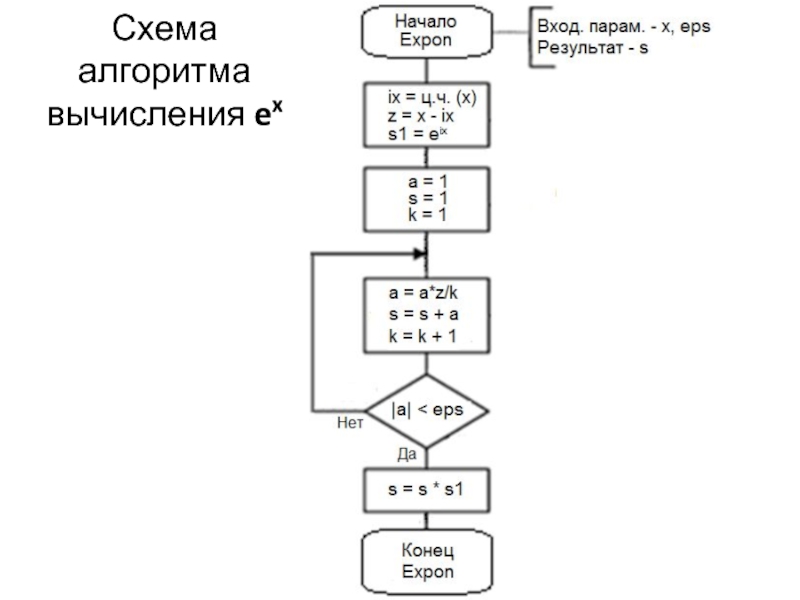
Слайд 12Приведение аргумента ex к диапазону|x| < 1
При больших по абсолютной величине
x = E(x) + z, где E(x) – целая часть x, 0<=z<1 – дробная часть x. Тогда ex = eE(x) ∙ ez, где eE(x) вычисляется путем возведения в целую степень, а ez – путем разложения в ряд.
Слайд 17Рекуррентные формулы и формулы приведения для функции arctg(x)
Нечетность: arctg(-x) = -arctg(x)
Приведение
Слайд 18Рекуррентные формулы и формулы приведения для функции ln(z)
Представим z в виде
ln 2 ≈ 0,6931471805599453
Слайд 23Многочленные приближения ex и ln x
ex ≈ a0x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7
a0 = 0,0002040 a1 =
a3 = 0,0416350 a4 = 0,1666674 a5 = 0,5000063
a6 = 1,0 a7 = 0,9999998
|x| <= 1 Δ = 2∙10-7
ln(1+x) ≈ a0x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7
a0 = 0,010757369 a1 = -0,055119959 a2 = 0,134639267
a3 = -0,225873284 a4 = 0,328233122 a5 = -0,499470150
a6 = 0,999981028 a7 = 0
|x| <= 1 Δ = 2∙10-7
Слайд 24Многочленные приближения sin x и cos x
sin x ≈ a0x9+a2x7+a4x5+a6x3+a8x
a0 =
a6 = -0,166666589 a8 = 1,000000002
|x| <= π/2 Δ = 6∙10-9
cos x ≈ a0x10+a2x8+a4x6+a6x4+a8x2+a10
a0 = -0,000000269591 a2 = 0,000024795132
a4 = -0,001388885683 a6 = 0,041666665950
a8 = -0,499999999942 a10 = 1,0
|x| <= 1 Δ = 2∙10-9
Слайд 25Многочленное приближение tg x
tg x ≈ a0x13+a2x11+a4x9+a6x7+a8x5+a10x3+a12x
a0 = 0,0095168091 a2 =
a6 = 0,0533740603 a8 = 0,1333923995 a10 = 0,3333314036
a12 = 1,0
|x| <= π/4 Δ = 2∙10-8
Слайд 26Вычисление функций методом итераций
Всякую функцию y = f(x) можно различными способами
………………………….
Условия сходимости: F'(x,y) и F''(x,y) существуют и знакопостоянны в окрестности корня уравнения
Правило останова: |yn+1 - yn| < ε – допустимая абс. погр.
Слайд 27Вычисление квадратного корня методом итераций
Пусть y = √x (x > 0).
Эта формула называется формулой Герона.
Выбор y0:
Если x>1, то x = 2mz, где m – целое число и 0,5≤z<1,
и y0 = 2E(m/2), где E(m/2) – целая часть числа m/2.
Если 0,01≤x≤1, то y0 = ax+b, a и b – из таблицы:
Слайд 29Вычисление корня p–й степени методом итераций
Пусть y = p√x (x >
F(x,y) = 1 – x/yp
Выбор y0
Слайд 30Вычисление корня p–й степени методом итераций. Формула Ньютона
Если преобразовать выражение y
F(x,y) = yp– x, то получим другую итерационную формулу:
известную как формула Ньютона. При p = 2
из формулы Ньютона получается формула Герона.












![Приведение аргумента sin(x) и cos(x) к отрезку [0; π/4]](/img/tmb/2/187573/33b3e486a4bcc38d8b19f09551b7fa60-800x.jpg)