- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вписані та описані чотирикутники презентация
Содержание
- 1. Вписані та описані чотирикутники
- 2. Пригадайте! Ви це знаєте!
- 3. - Чи може центральний кут бути тупим?
- 4. - Центральний кут дорівнює 104°. Знайдіть градусну
- 5. - Для якого трикутника центр вписаного кола
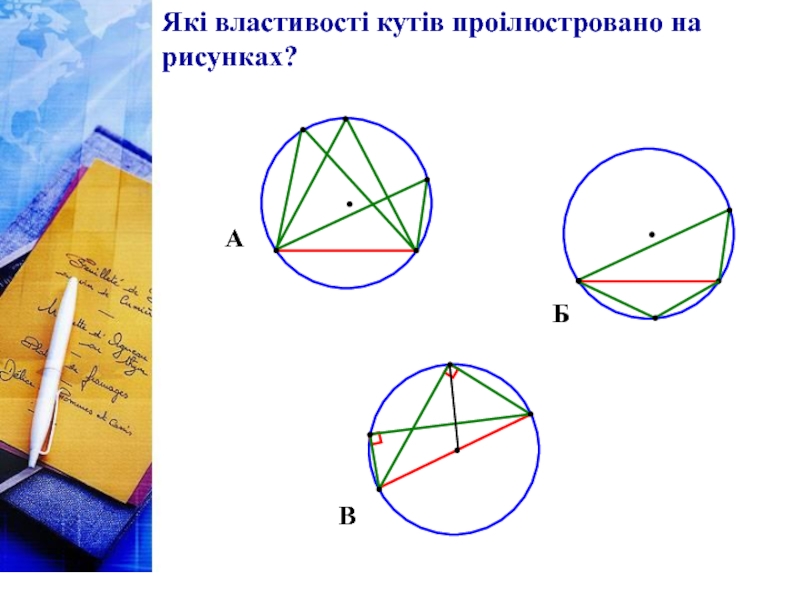
- 6. Які властивості кутів проілюстровано на рисунках?
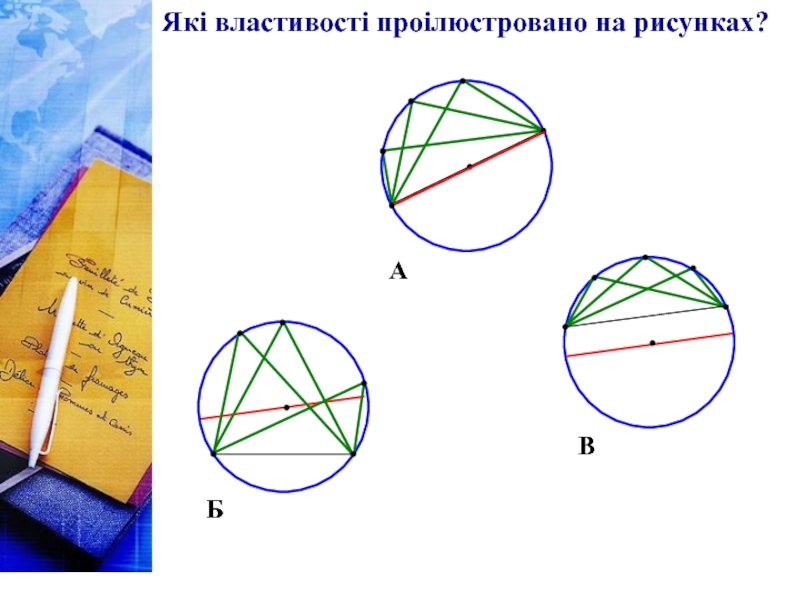
- 7. А Б В Які властивості проілюстровано на рисунках?
- 8. Чим більше я треную свій мозок ,
- 9. Вписані та описані чотирикутники
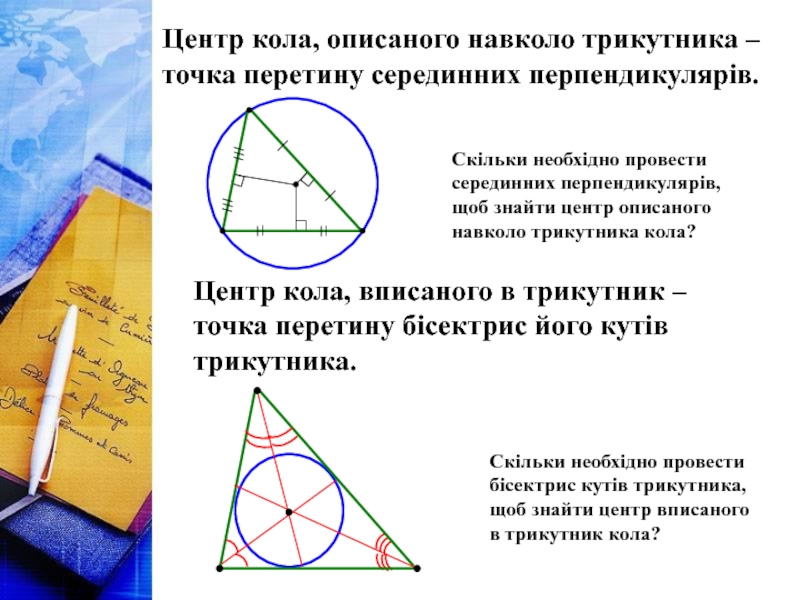
- 10. Центр кола, описаного навколо трикутника – точка
- 12. Центр кола, описаного навколо чотирикутника – точка
- 13. Теорема 10.1 Якщо чотирикутник є вписаним
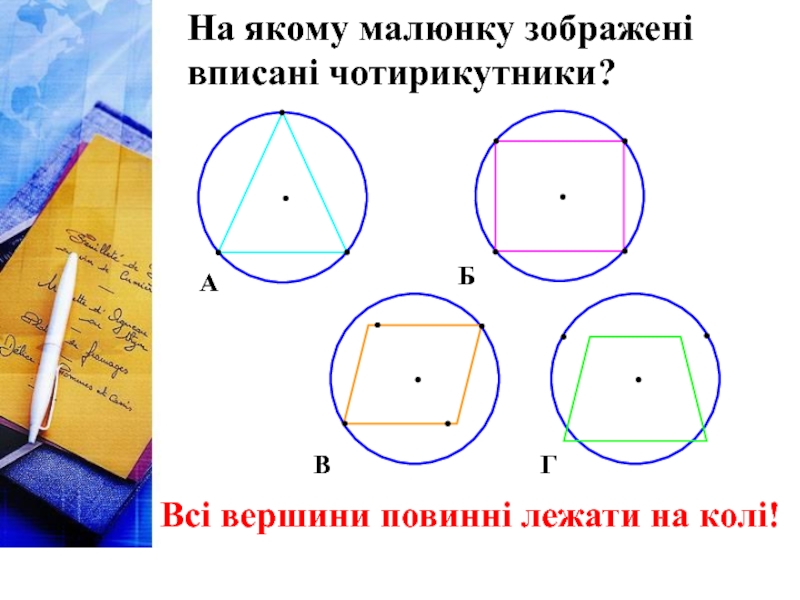
- 14. А Б В Г На якому малюнку
- 15. Центр кола, вписаного в чотирикутник – точка
- 16. Теорема 10.3 Якщо чотирикутник є описаним
- 17. Теорія мертва без практики…
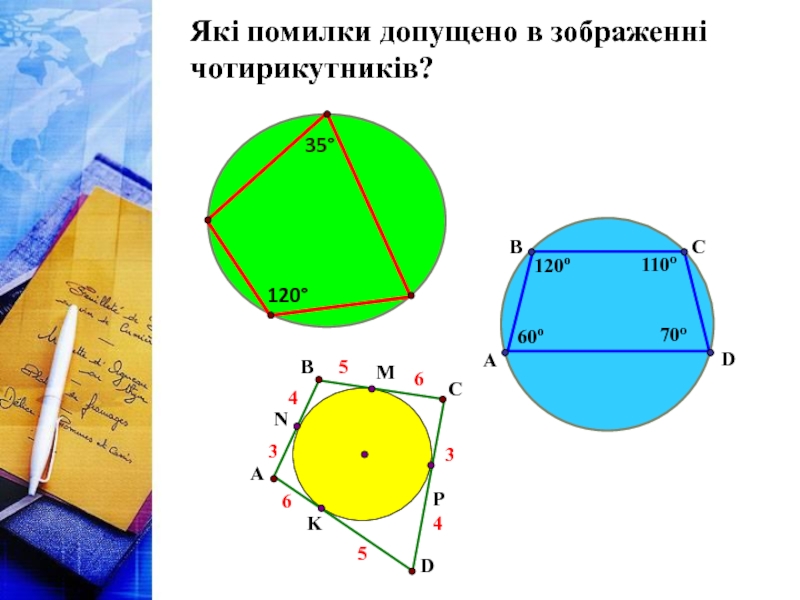
- 18. Які помилки допущено в зображенні чотирикутників?
- 19. Теорія мертва без практики…
- 22. Якщо не висловлено різні думки, немає з чого вибирати краще
- 23. У яких чотирикутниках сума
- 24. У яких чотирикутниках суми
- 25. «Як приємно зрозуміти, що ти чогось дізнався» Ж.Мольєр
- 26. Що нового я дізнався? Яке завдання
- 27. Домашнє завдання: Читати п.10, вивчити означення
Слайд 3- Чи може центральний кут бути тупим?
- Градусна міра вписаного
- Знайдіть кутову міру половини кола.
- Знайдіть градусну міру вписаного кута, який спирається на третю частину кола.
- Знайдіть центральний кут, якщо відповідний вписаний кут прямий.
- Вписаний кут дорівнює 50°. Знайдіть градусну міру відповідного йому центрального кута.
Слайд 4- Центральний кут дорівнює 104°. Знайдіть градусну міру відповідного вписаного кута.
- Чи в кожний трикутник можна вписати коло?
- Центр вписаного в трикутник кола знаходиться в точці перетину...
- Знайдіть градусну міру вписаного кута, який спирається на діаметр кола.
- Центр кола, описаного навколо трикутника, знаходиться в точці перетину…
Слайд 5- Для якого трикутника центр вписаного кола лежить всередині трикутника?
- Для
- На середині гіпотенузи знаходиться центр … кола.
- Для гострокутного трикутника центр описаного кола знаходиться …
Слайд 10Центр кола, описаного навколо трикутника – точка перетину серединних перпендикулярів.
Центр
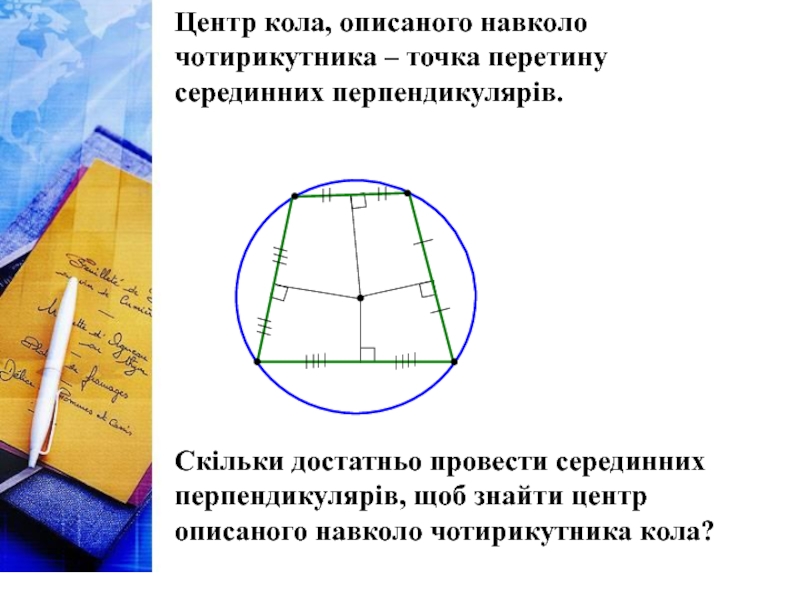
Скільки необхідно провести серединних перпендикулярів, щоб знайти центр описаного навколо трикутника кола?
Скільки необхідно провести бісектрис кутів трикутника, щоб знайти центр вписаного в трикутник кола?
Слайд 12Центр кола, описаного навколо чотирикутника – точка перетину серединних перпендикулярів.
Скільки
Слайд 13Теорема 10.1
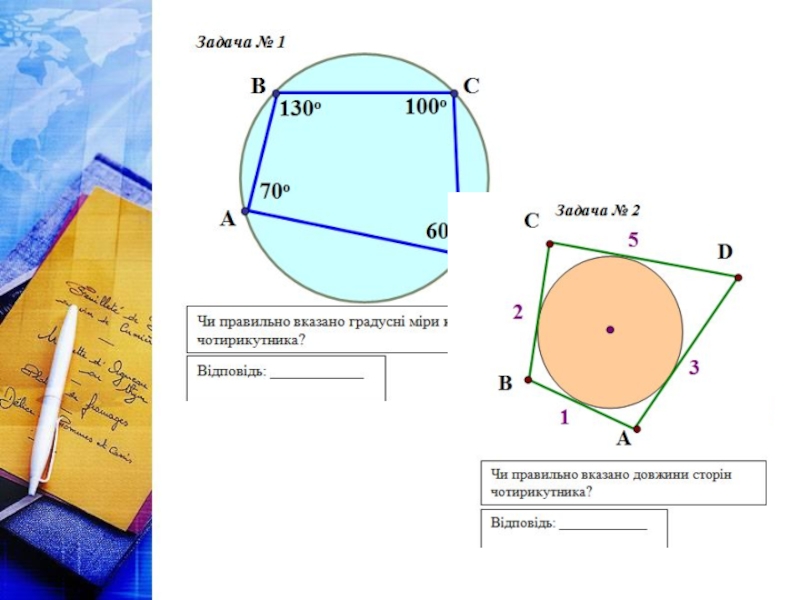
Якщо чотирикутник є вписаним у коло, то сума його
Теорема 10.2 (обернена до теореми 10.1)
Якщо в чотирикутнику сума протилежних кутів дорівнює 180о, то навколо нього можна описати коло.
∠1+∠2 = ∠3 +∠4
Слайд 14А
Б
В
Г
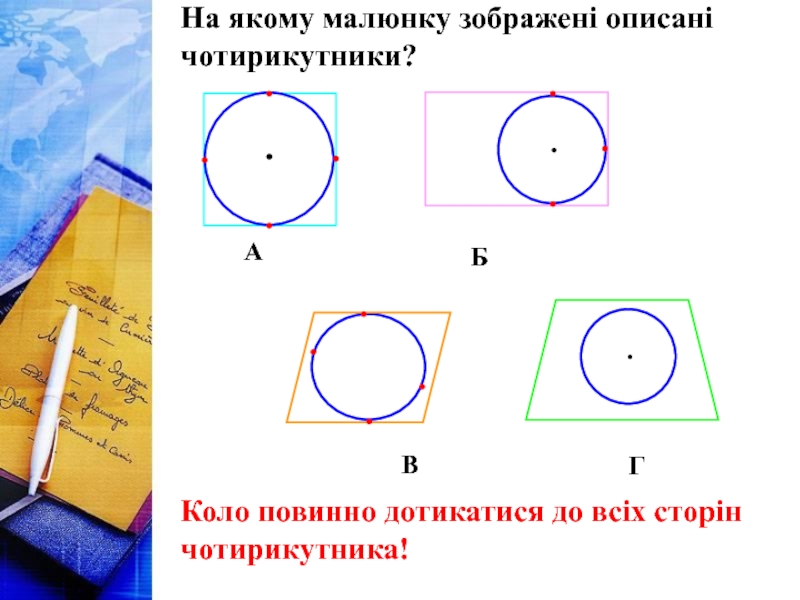
На якому малюнку зображені описані чотирикутники?
Коло повинно дотикатися до всіх сторін
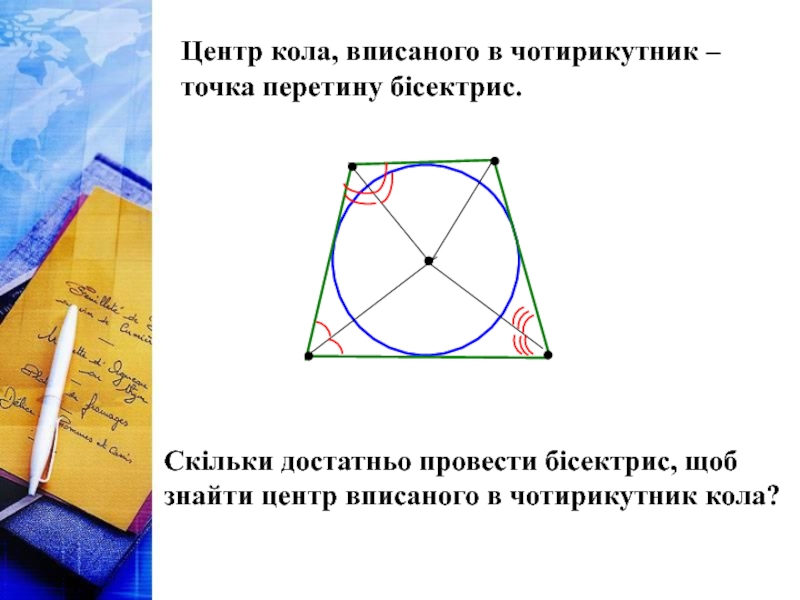
Слайд 15Центр кола, вписаного в чотирикутник – точка перетину бісектрис.
Скільки достатньо
Слайд 16Теорема 10.3
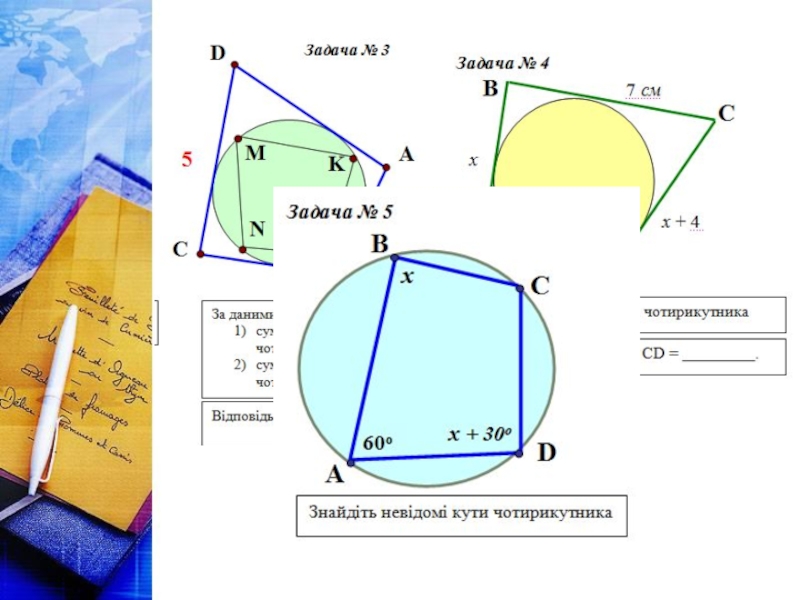
Якщо чотирикутник є описаним навколо кола, то суми його
Теорема 10.4 (обернена до теореми 10.3)
Якщо в опуклому чотирикутнику суми протилежних сторін рівні, то в нього можна вписати коло.
a + c = b + d
Слайд 23
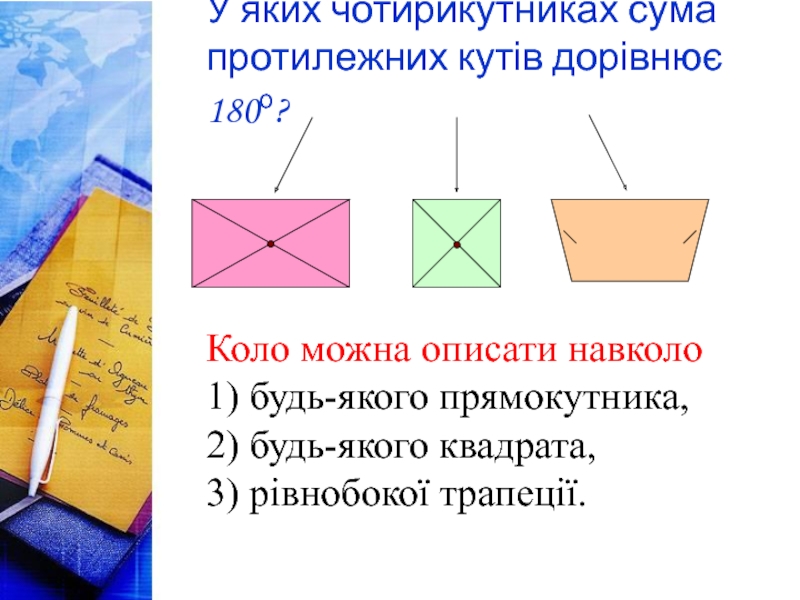
У яких чотирикутниках сума протилежних кутів дорівнює 180о?
Коло можна описати
1) будь-якого прямокутника,
2) будь-якого квадрата,
3) рівнобокої трапеції.
Слайд 24
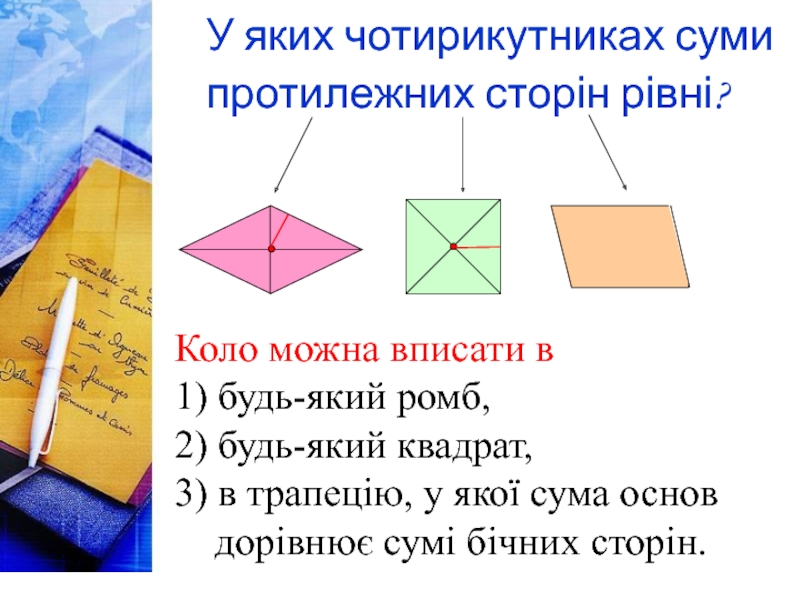
У яких чотирикутниках суми протилежних сторін рівні?
Коло можна вписати в
1) будь-який ромб,
2) будь-який квадрат,
3) в трапецію, у якої сума основ дорівнює сумі бічних сторін.
Слайд 27Домашнє завдання:
Читати п.10, вивчити означення та теореми.
Розібрати та вивчити таблицю
Виконати № 331, 339, 343* (стор. 67)