Кировской области
учитель математики
Дягилева Л. В.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов презентация
Содержание
- 1. Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов
- 2. Цели урока Знать: определение вектора в пространстве
- 3. Физические величины Скорость Ускорение
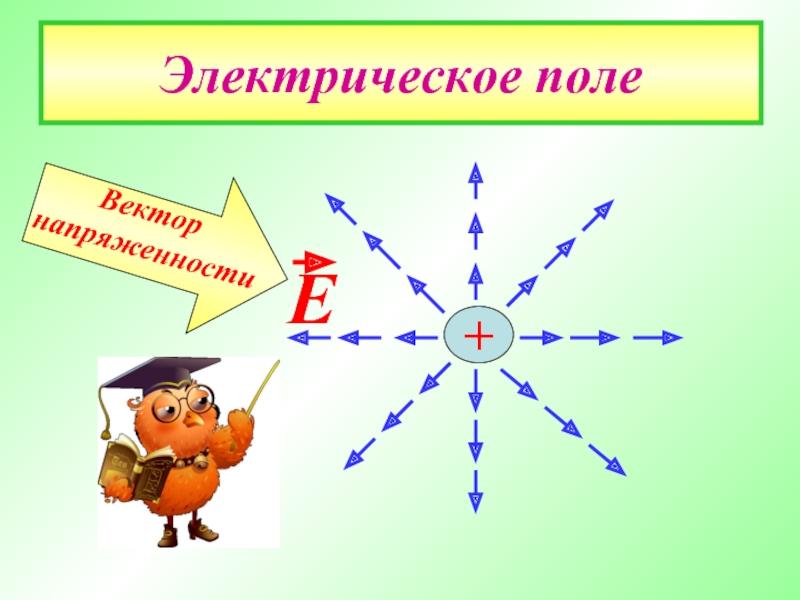
- 4. Электрическое поле Е
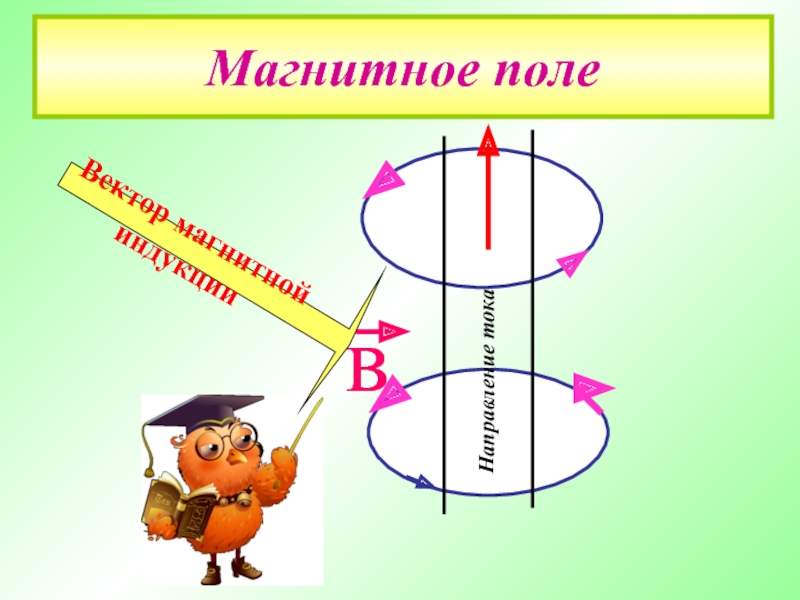
- 5. Магнитное поле Направление тока в
- 6. Понятие вектора появилось в 19 веке в
- 7. Современная символика для обозначения вектора r была
- 8. Задание Записать все термины по теме
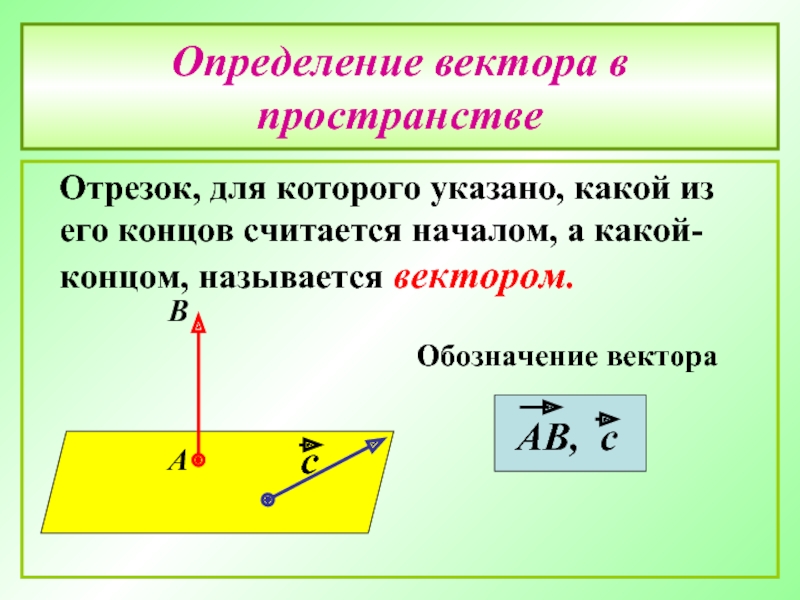
- 9. Определение вектора в пространстве Отрезок,
- 10. Т Любая точка пространства также
- 11. Длина ненулевого вектора Длиной
- 12. Определение коллинеарности векторов Два ненулевых вектора
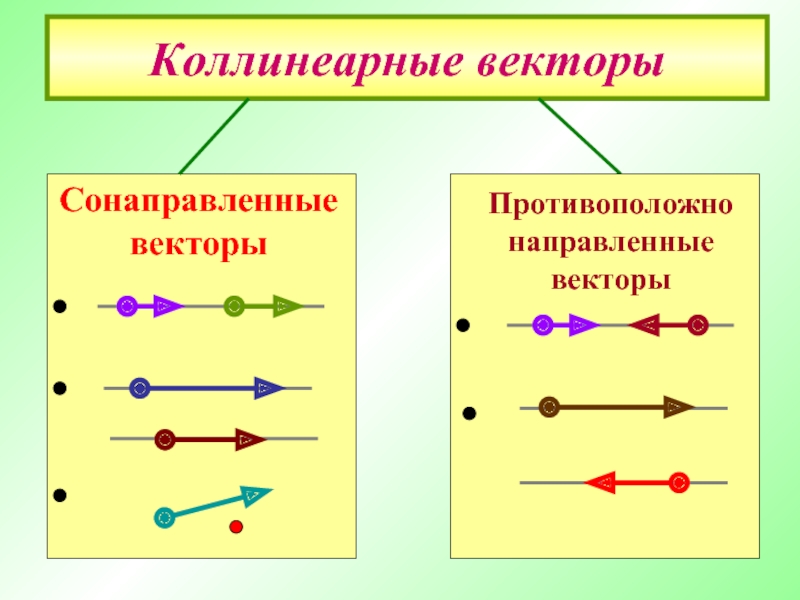
- 13. Коллинеарные векторы
- 14. Какие векторы на рисунке сонаправленные? Какие векторы
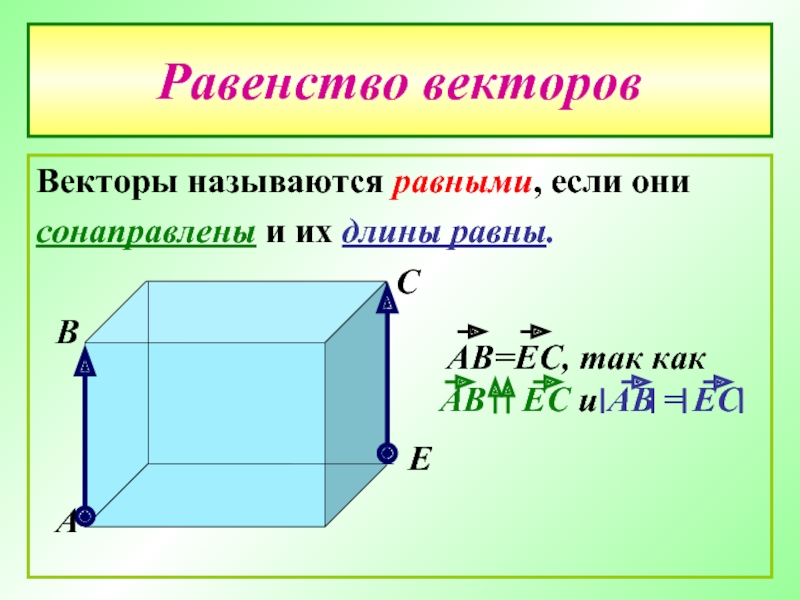
- 15. Равенство векторов Векторы называются равными, если они
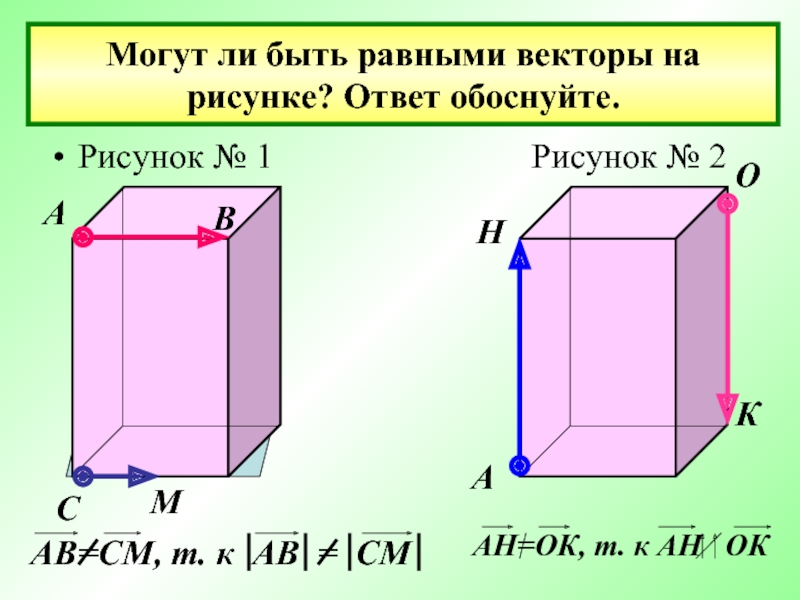
- 16. Могут ли быть равными векторы на
- 17. Доказать, что от любой точки пространства
- 18. Решение задач № 322
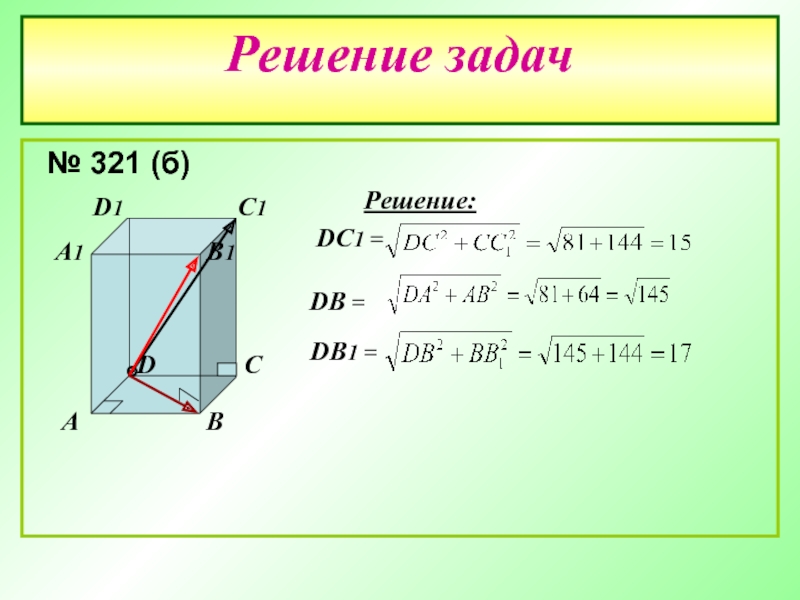
- 19. Решение задач № 321 (б)
- 20. Решение задач А D С В М
- 21. По условию все ребра
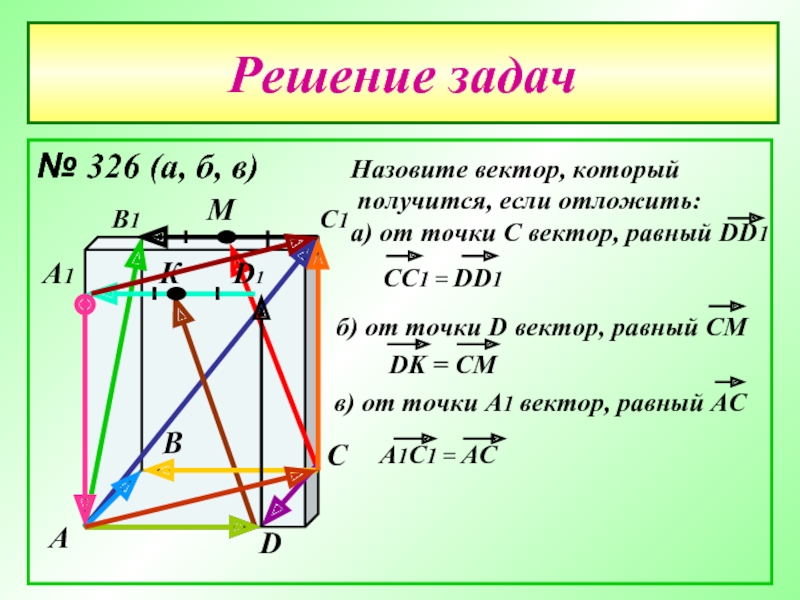
- 22. Решение задач № 326 (а, б, в)
- 23. Самостоятельная работа Дан тетраэдр МАВС, угол АСВ
- 24. Кроссворд Г А
- 25. Домашнее задание
- 26. Перемена
- 27. Список литературы: 1. «Геометрия
Цели урока Знать: определение вектора в пространстве и связанные с ним понятия; равенство векторов. Уметь: решать задачи по данной теме.
Слайд 2Цели урока
Знать: определение вектора в пространстве и связанные с ним понятия;
равенство векторов.
Уметь: решать задачи по данной теме.
Уметь: решать задачи по данной теме.
Слайд 7Современная символика для обозначения вектора r была введена в 1853 году
французским математиком О. Коши.
Слайд 8 Задание
Записать все термины по теме «Векторы на плоскости».
Вектор
Нулевой вектор
Длина вектора
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные векторы
Равенство векторов
Слайд 9Определение вектора в пространстве
Отрезок, для которого указано, какой из
его концов считается началом, а какой- концом, называется вектором.
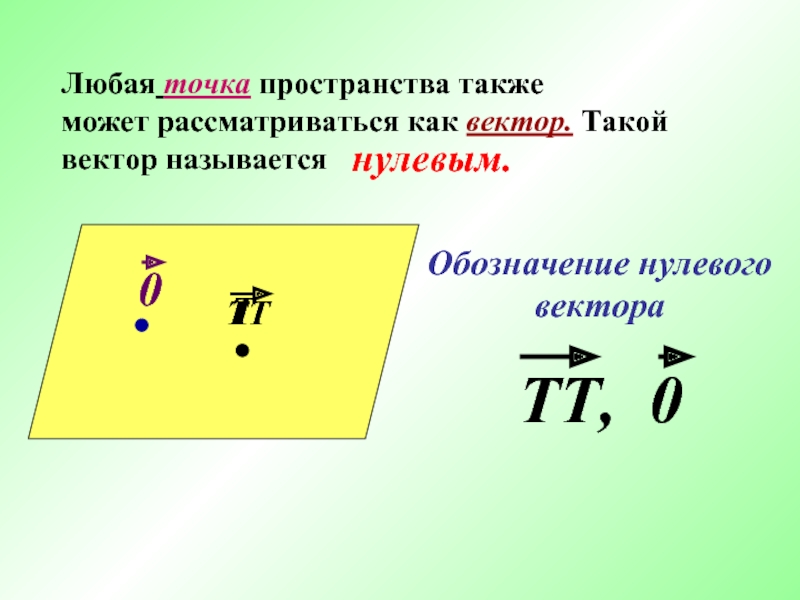
Слайд 10
Т
Любая точка пространства также
может рассматриваться как вектор. Такой вектор называется
нулевым.
Слайд 11
Длина ненулевого вектора
Длиной вектора АВ называется длина отрезка АВ.
Длина вектора
АВ (вектора а) обозначается так:
АВ , а
Длина нулевого вектора считается равной нулю:
АВ , а
Длина нулевого вектора считается равной нулю:
0
= 0
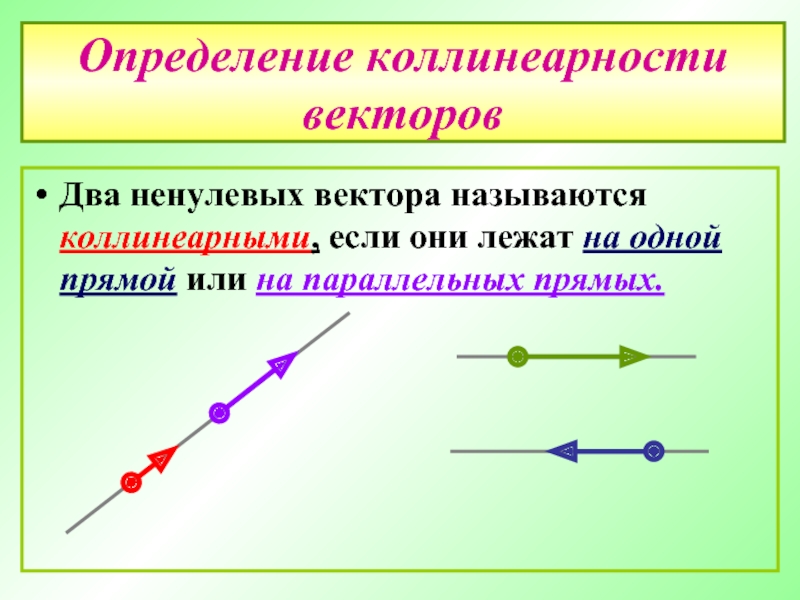
Слайд 12Определение коллинеарности векторов
Два ненулевых вектора называются коллинеарными, если они лежат
на одной прямой или на параллельных прямых.
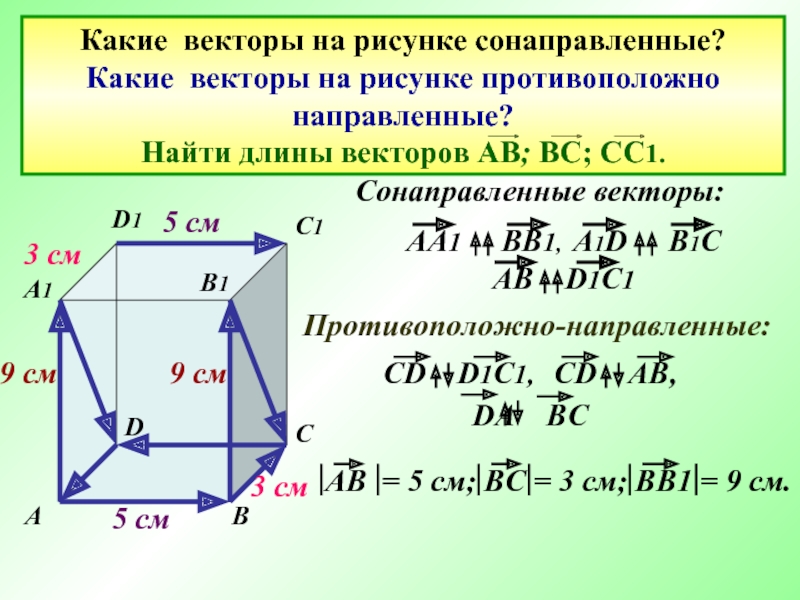
Слайд 14Какие векторы на рисунке сонаправленные? Какие векторы на рисунке противоположно направленные? Найти длины
векторов АВ; ВС; СС1.
A
B
C
D
В1
D1
A1
C1
Сонаправленные векторы:
Противоположно-направленные:
5 см
3 см
9 см
5 см
3 см
9 см
Слайд 17
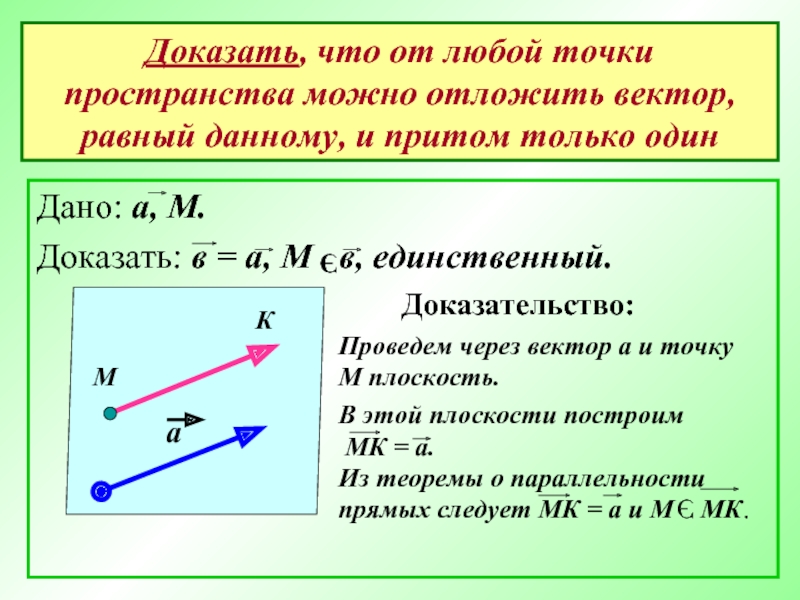
Доказать, что от любой точки пространства можно отложить вектор, равный данному,
и притом только один
Дано: а, М.
Доказать: в = а, М в, единственный.
Доказательство:
Проведем через вектор а и точку
М плоскость.
М
К
Слайд 18Решение задач
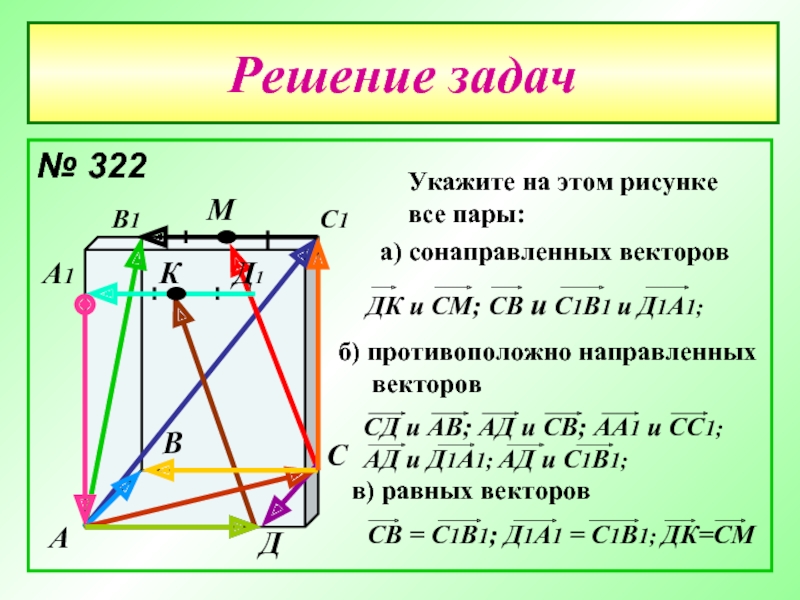
№ 322
А
В
С
Д
А1
В1
С1
Д1
М
К
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
б) противоположно
направленных
векторов
векторов
в) равных векторов
Слайд 20Решение задач
А
D
С
В
М
Р
N
Q
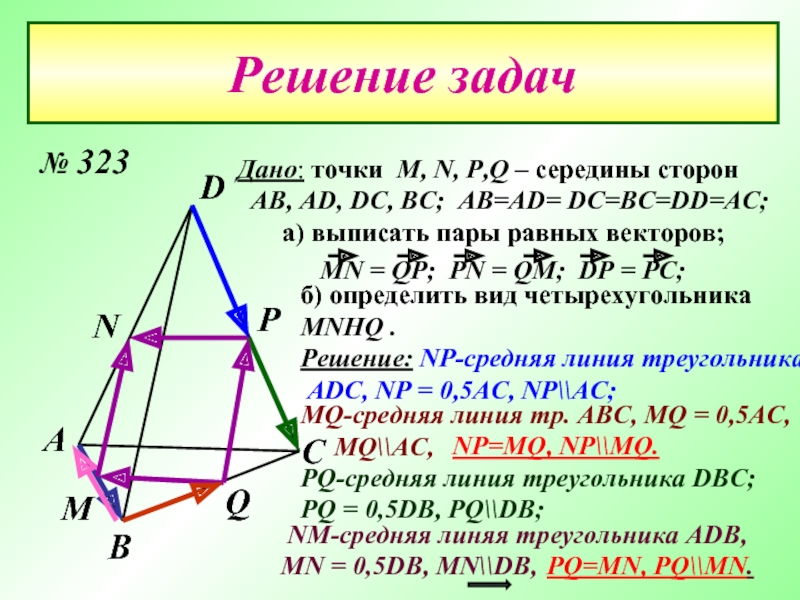
Дано: точки М, N, P,Q – середины сторон
AB, AD,
DC, BC; AB=AD= DC=BC=DD=AC;
а) выписать пары равных векторов;
б) определить вид четырехугольника
MNHQ .
NM-средняя линяя треугольника ADB,
MN = 0,5DB, MN\\DB,
MQ-средняя линия тр. ABC, MQ = 0,5AC,
MQ\\AC,
Решение: NP-средняя линия треугольника
ADC, NP = 0,5AC, NP\\AC;
NP=MQ, NP\\MQ.
PQ-средняя линия треугольника DВC;
PQ = 0,5DB, PQ\\DB;
PQ=MN, PQ\\MN.
№ 323
Слайд 21 По условию все ребра тетраэдра равны, то он
правильный и скрещивающиеся ребра в нем перпендикулярны.
DB перпендикулярно АС .
DB перпендикулярно АС .
NP=MQ=PQ=MN
NP\\MQ
MN\\PQ
MNPQ-
квадрат
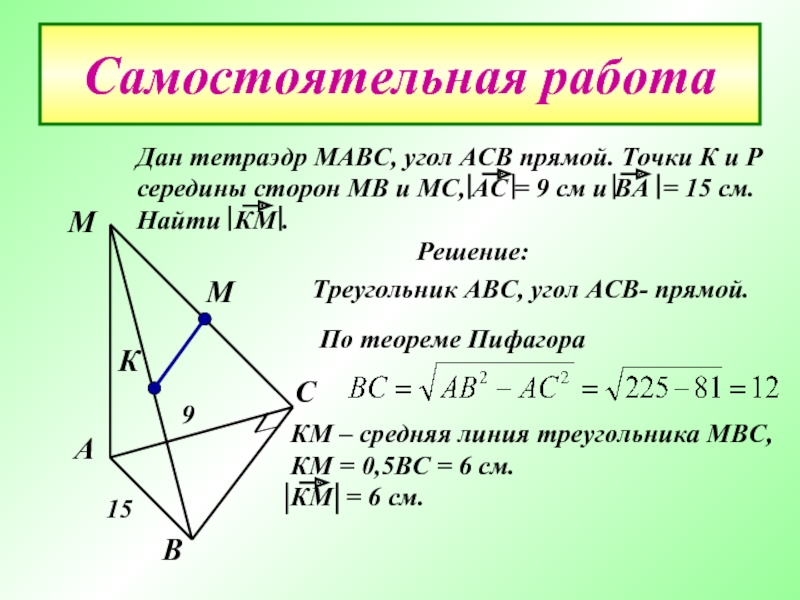
Слайд 23Самостоятельная работа
Дан тетраэдр МАВС, угол АСВ прямой. Точки К и Р
середины сторон МВ и МС, АС = 9 см и ВА = 15 см. Найти КМ .
Решение:
Решение:
М
А
В
С
К
М
Треугольник АВС, угол АСВ- прямой.
9
15
По теореме Пифагора
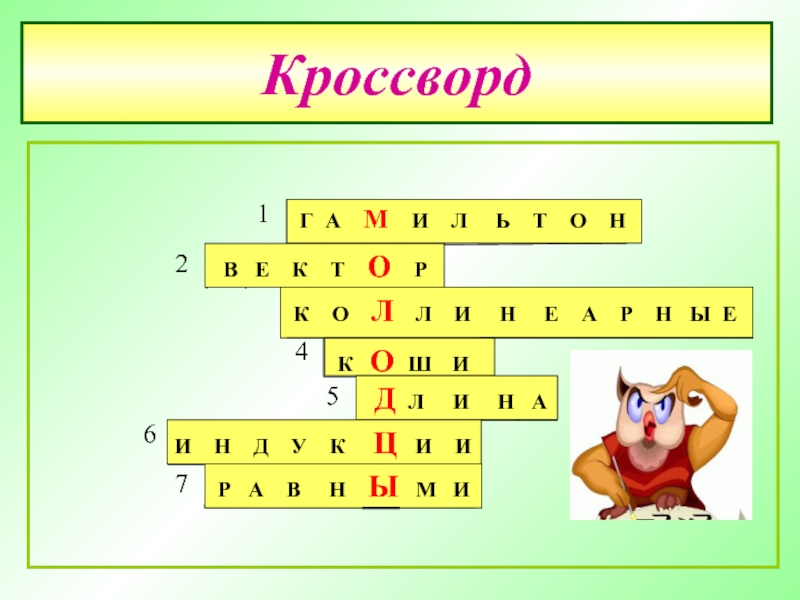
Слайд 24Кроссворд
Г А М И Л
Ь Т О Н
В Е К Т О Р
К О Л Л И Н Е А Р Н Ы Е
К О Ш И
Д Л И Н А
И Н Д У К Ц И И
Р А В Н Ы М И
1
2
4
5
6
7
Слайд 27 Список литературы:
1. «Геометрия 10-11» Учебник для общеобразовательных учреждений.
Л. С. Атанасян, И. Ф. Бутузов, С. Б. Кадомцев и др. М.: Просвещение, 2010.
2. Энциклопедический словарь юного математика. Сост. Э 68 А.. П. Савин.- М. Педагогика, 1985.
3. Поурочные разработки по геометрии: 10 класс (сост. В. А. Яровенко) в помощь школьному учителю- М.: ВАКО, 2007.
4 Сайты:
http://images.yandex.ru/yandsearch?ed=1&text=%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%BD%D0%B0%20%D1%88%D0%BA%D0%BE%D0%BB%D1%8C%D0%BD%D1%83%D1%8E%20%D1%82%D0%B5%D0%BC%D1%83&p=1&img_url=img1.liveinternet.ru%2Fimages%2Fattach%2Fc%2F3%2F76%2F873%2F76873211_default.jpg&rpt=simage
http://images.yandex.ru/yandsearch?ed=1&text=%D0%9A%D0%B0%D1%80%D1%82%D0%D0%BB%D1%8C%D0%BD%D1%83%D1%8E%20%D1%82%D0%B5%D0%BC%D1%83&img_url=i.allday.ru%2Fuploads%2Fposts%2Fthumbs%2F1217821185_12.jpg&rpt=simage&p=2
http://images.yandex.ru/yandsearch?text=%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D1%8B%20%D0%B2%20%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8%20%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8&img_url=www.statistica.com.au%2FMATHSC%257E1%2Fimg560.gif&rpt=simage&p=145
http://ru.wikipedia.org/wiki/Файл:Cauchy_Augustin_Louis_dibner_coll_SIL14-C2-03a.jpg
http://ru.wikipedia.org/wiki/Файл:William_Rowan_Hamilton_painting.jpg
http://ru.wikipedia.org/wiki/Файл:Hgrassmann.jpg
2. Энциклопедический словарь юного математика. Сост. Э 68 А.. П. Савин.- М. Педагогика, 1985.
3. Поурочные разработки по геометрии: 10 класс (сост. В. А. Яровенко) в помощь школьному учителю- М.: ВАКО, 2007.
4 Сайты:
http://images.yandex.ru/yandsearch?ed=1&text=%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8%20%D0%BD%D0%B0%20%D1%88%D0%BA%D0%BE%D0%BB%D1%8C%D0%BD%D1%83%D1%8E%20%D1%82%D0%B5%D0%BC%D1%83&p=1&img_url=img1.liveinternet.ru%2Fimages%2Fattach%2Fc%2F3%2F76%2F873%2F76873211_default.jpg&rpt=simage
http://images.yandex.ru/yandsearch?ed=1&text=%D0%9A%D0%B0%D1%80%D1%82%D0%D0%BB%D1%8C%D0%BD%D1%83%D1%8E%20%D1%82%D0%B5%D0%BC%D1%83&img_url=i.allday.ru%2Fuploads%2Fposts%2Fthumbs%2F1217821185_12.jpg&rpt=simage&p=2
http://images.yandex.ru/yandsearch?text=%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80%D1%8B%20%D0%B2%20%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8%20%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8&img_url=www.statistica.com.au%2FMATHSC%257E1%2Fimg560.gif&rpt=simage&p=145
http://ru.wikipedia.org/wiki/Файл:Cauchy_Augustin_Louis_dibner_coll_SIL14-C2-03a.jpg
http://ru.wikipedia.org/wiki/Файл:William_Rowan_Hamilton_painting.jpg
http://ru.wikipedia.org/wiki/Файл:Hgrassmann.jpg
