1
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра: Матрицы. Действия с матрицами. Определитель. Его вычисление и основные свойства презентация
Содержание
- 1. Алгебра: Матрицы. Действия с матрицами. Определитель. Его вычисление и основные свойства
- 2. Матрицы. Определение: Матрица размерности mxn – это
- 3. Матрицы. 3 Нулевая матрица Побочная диагональ
- 4. Действия над матрицами. Сложение матриц: 4 Вычитание матриц: Умножение матрицы на число:
- 5. Действия над матрицами Умножение матриц: 5
- 6. Пример умножения матриц. 6
- 7. Действия над матрицами. Операции сложения и умножения
- 8. Определитель матрицы. Каждой квадратной матрице ставится
- 9. Вычисление определителя. Для матрицы размера 2х2, определитель
- 10. Вычисление определителя. Будем называть минором (Mkl) определитель
- 11. Вычисление определителя. Алгебраическим дополнением элемента матрицы с
- 12. Вычисление определителя. Определитель матрицы размера более чем
- 13. Вычисление определителя. Для вычисления определителя матрицы 3х3 можно использовать следующую формулу: 13
- 14. Пример вычисление определителя. 14
- 15. Пример вычисление определителя. 15
- 16. Пример вычисление определителя. 16
- 17. Свойства определителей. 17 Свойство 1. При перестановке
- 18. Свойства определителей. 18 Свойство 5. Если все
- 19. Система линейных алгебраических уравнений (СЛАУ) Система вида:
- 20. Система линейных алгебраических уравнений (СЛАУ) Если обозначим:
- 21. Система линейных алгебраических уравнений (СЛАУ) 21 Обратная
- 22. Система линейных алгебраических уравнений (СЛАУ) Геометрически, каждое
- 23. Система линейных алгебраических уравнений (СЛАУ) 23 2.Пересечение по прямой: 3.Нет общих точек пересечения:
- 24. Система линейных алгебраических уравнений (СЛАУ) В первом
- 25. Метод Крамера. Данный метод сводиться к нахождению четырех определителей: 25
- 26. Метод Крамера. В результате получим решение СЛАУ: 26
- 27. Метод Крамера. Пример. Решить систему уравнений: 27
- 28. Метод Крамера. Пример. Вычислим определитель системы: 28
- 29. Метод Крамера. Пример. 29
- 30. Метод Крамера. Пример. 30
- 31. Метод Крамера. Пример. 31
- 32. Метод Крамера. Пример. В результате мы получили: D=5, D1=0, D2=0, D3=10. 32
- 33. Метод Крамера. Пример. 33
- 34. Решение СЛАУ методом обратной матрицы. 34
- 35. Решение СЛАУ методом обратной матрицы. 35
- 36. Решение СЛАУ методом обратной матрицы. 36
- 37. Решение СЛАУ методом обратной матрицы. 37
- 38. Метод Гаусса Расширенной матрицей системы 38 будем называть матрицу вида
- 39. Метод Гаусса Ранг матрицы – это размер
- 40. Метод Гаусса Для того, чтобы СЛАУ была
- 41. Метод Гаусса Сам метод Гаусса состоит в
- 42. Метод Гаусса 42
- 43. Метод Гаусса 43 Вычитаем из 3 строки
- 44. Метод Гаусса 44 Теперь из расширенной матрицы запишем получившуюся систему:
- 45. Метод Гаусса Осталось только решить нашу систему.
- 46. Метод Гаусса Исследовать СЛАУ на совместность: 46 Запишем расширенную матрицу системы:
- 47. Метод Гаусса 47 Вычитаем из 2 строки
- 48. Метод Гаусса Заметим, что наибольший ненулевой минор
- 49. Метод Гаусса Исследовать СЛАУ на совместность: 49 Запишем расширенную матрицу системы:
- 50. Метод Гаусса 50 Вычитаем из 2 строки
- 51. Метод Гаусса Заметим, что наибольший ненулевой минор
Матрицы. Определение: Матрица размерности mxn – это таблица чисел расположенных в m строках и n столбцах вида 2 Матрицы бывают квадратные: Прямоугольные: или
Слайд 1Лекция №1
Алгебра:
Матрицы. Действия с матрицами.
Определитель. Его вычисление и основные свойства. Система
линейных алгебраических уравнений (СЛАУ). Методы решения СЛАУ.
Слайд 2Матрицы.
Определение: Матрица размерности mxn – это таблица чисел расположенных в m
строках и n столбцах вида
2
Матрицы бывают квадратные:
Прямоугольные: или
Слайд 3Матрицы.
3
Нулевая матрица
Побочная диагональ
Главная диагональ
Единичная матрица
Матрица столбец
Матрица строка
Слайд 7Действия над матрицами.
Операции сложения и умножения матриц обладают следующими свойствами:
Сложения:
А+В=В+А (переместительный
закон)
А+(В+С)=(А+В)+С (сочетательный закон)
А+0=А
(α·β)·А= α·(β·А)
(α+β)·А= α·А+β·А (распределительный
(А+В)·α=α·А+α·В закон)
Умножения:
1. А·В≠В·А
2. А·(В·С)= (А·В)·С
3. А·(В+С)= А·В+А·С
(А+В)·С= А·С+В·С
4. А·Е= Е·А=А
А+(В+С)=(А+В)+С (сочетательный закон)
А+0=А
(α·β)·А= α·(β·А)
(α+β)·А= α·А+β·А (распределительный
(А+В)·α=α·А+α·В закон)
Умножения:
1. А·В≠В·А
2. А·(В·С)= (А·В)·С
3. А·(В+С)= А·В+А·С
(А+В)·С= А·С+В·С
4. А·Е= Е·А=А
7
Слайд 8Определитель матрицы.
Каждой квадратной матрице ставится в соответствие число, называемое определителем матрицы.
Обозначается:
det|A| или ||A|| или |A|
8
Слайд 9Вычисление определителя.
Для матрицы размера 2х2, определитель вычисляется по следующей формуле:
9
Для вычисления
определителя матрицы размера 3х3 (nxn), введем понятие миноров и алгебраических дополнений.
Слайд 10Вычисление определителя.
Будем называть минором (Mkl) определитель матрицы полученной из исходной после
вычеркивания из нее k-ой строки и l-го столбца.
10
Слайд 11Вычисление определителя.
Алгебраическим дополнением элемента матрицы с индексами k, l называется число
, полученное умножением минора (Mkl) на (-1) в степени (k+l).
11
Слайд 12Вычисление определителя.
Определитель матрицы размера более чем 3х3, вычисляется путем разложения этой
матрицы по строке или столбцу, следующим образом:
12
Слайд 13Вычисление определителя.
Для вычисления определителя матрицы 3х3 можно использовать следующую формулу:
13
Слайд 17Свойства определителей.
17
Свойство 1. При перестановке двух строк (или столбцов) определитель меняет
знак.
Свойство 2. Общий множитель какой-либо строки или столбца можно выносить за знак определителя.
Свойство 3. Если в определителе две строки (или два столбца) пропорциональны (в частности, равны), то определитель равен нулю.
Свойство 4. При замене всех строк определителя на столбцы с теми же номерами величина его не изменится.
Свойство 2. Общий множитель какой-либо строки или столбца можно выносить за знак определителя.
Свойство 3. Если в определителе две строки (или два столбца) пропорциональны (в частности, равны), то определитель равен нулю.
Свойство 4. При замене всех строк определителя на столбцы с теми же номерами величина его не изменится.
Слайд 18Свойства определителей.
18
Свойство 5. Если все элементы некоторой строки (столбца) нули, то
определитель равен нулю.
Свойство 6. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.
Свойство 7. Сумма парных произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения другой строки (столбца) равна нулю.
Свойство 6. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.
Свойство 7. Сумма парных произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения другой строки (столбца) равна нулю.
Слайд 19Система линейных алгебраических уравнений (СЛАУ)
Система вида:
где матрица системы,
- вектор неизвестных,
- вектор правой части уравнения,
называется системой линейных алгебраических уравнений (СЛАУ).
называется системой линейных алгебраических уравнений (СЛАУ).
19
Слайд 20Система линейных алгебраических уравнений (СЛАУ)
Если обозначим:
20
То нашу систему можно записать в
виде:
Тогда решение будет иметь вид:
где обратная матрица системы.
Слайд 21Система линейных алгебраических уравнений (СЛАУ)
21
Обратная матрица – это такая матрица при
умножении на которую самой матрицы получается единичная матрица.
Слайд 22Система линейных алгебраических уравнений (СЛАУ)
Геометрически, каждое уравнение нашей системы является уравнением
плоскости. Возможны следующие варианты взаимного расположения трех плоскостей:
22
1.Пересечение в одной точке:
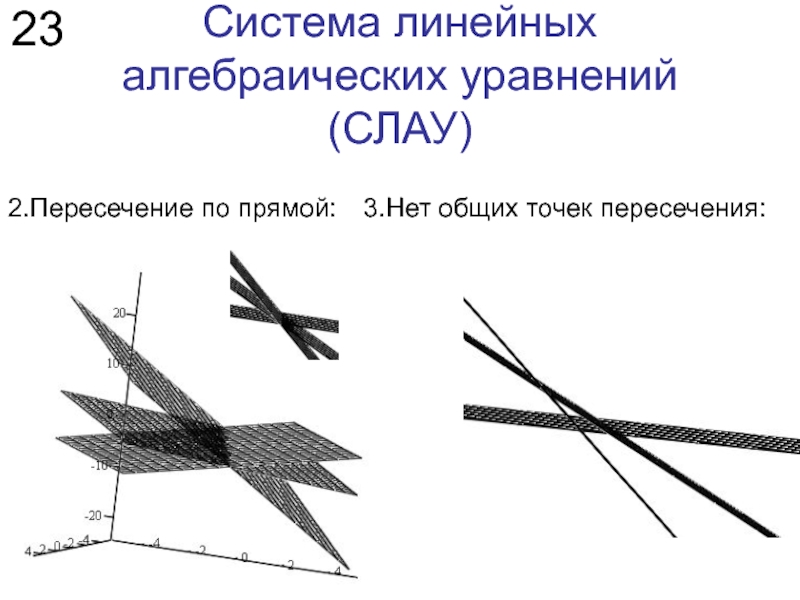
Слайд 23Система линейных алгебраических уравнений (СЛАУ)
23
2.Пересечение по прямой:
3.Нет общих точек пересечения:
Слайд 24Система линейных алгебраических уравнений (СЛАУ)
В первом случае определитель нашей системы НЕ
равен нулю, а значит решение существует и единственно.
Найти решение такой системы мы можем двумя методами: 1. Методом Крамера, 2. Методом обратной матрицы.
Во втором случае решений системы бесконечно много, и решить эту системы мы можем при помощи метода Гаусса.
В третьем случае система не имеет решения, проверить это можно также методом Гаусса.
Найти решение такой системы мы можем двумя методами: 1. Методом Крамера, 2. Методом обратной матрицы.
Во втором случае решений системы бесконечно много, и решить эту системы мы можем при помощи метода Гаусса.
В третьем случае система не имеет решения, проверить это можно также методом Гаусса.
24
Слайд 39Метод Гаусса
Ранг матрицы – это размер наибольшего ненулевого минора этой матрицы.
Ранг
матрицы с ненулевым определителем равен размеру этой матрицы.
39
Слайд 40Метод Гаусса
Для того, чтобы СЛАУ была совместна ранг матрицы системы должен
быть равен рангу расширенной матрицы.
Заметим:
Если ранг матрицы системы равен размерности самой матрицы, то система имеет единственное решение.
2. Если ранг матрицы системы равен рангу расширенной матрицы, но меньше размерности самой матрицы системы, то система имеет бесконечное множество решений.
3. Если ранг матрицы системы меньше ранга расширенной матрицы, то система несовместна и решений не существует.
Заметим:
Если ранг матрицы системы равен размерности самой матрицы, то система имеет единственное решение.
2. Если ранг матрицы системы равен рангу расширенной матрицы, но меньше размерности самой матрицы системы, то система имеет бесконечное множество решений.
3. Если ранг матрицы системы меньше ранга расширенной матрицы, то система несовместна и решений не существует.
40
Слайд 41Метод Гаусса
Сам метод Гаусса состоит в том, чтобы преобразованием строк получить
нули под главной диагональю расширенной матрицы системы.
41
Слайд 45Метод Гаусса
Осталось только решить нашу систему. Из последнего уравнения получаем z=2,
подставляем это значение z во второе уравнение и получаем y=0, теперь подставляем значение y в первое уравнение и получаем x=0.
45
Слайд 47Метод Гаусса
47
Вычитаем из 2 строки первую
Вычитаем из 3 строки первую умноженную
на 3
Вычитаем из 3 строки вторую
Вычитаем из 3 строки вторую
Слайд 48Метод Гаусса
Заметим, что наибольший ненулевой минор имеет размерность 2, а количество
неизвестных системы равно 3, т.е. ранг системы совпадает с рангом расширенной матрицы, но он меньше чем количество неизвестных системы – это означает, что наша система имеет бесконечное множество решений.
48
Слайд 50Метод Гаусса
50
Вычитаем из 2 строки первую
Вычитаем из 3 строки первую умноженную
на 3
Вычитаем из 3 строки вторую
Вычитаем из 3 строки вторую
Слайд 51Метод Гаусса
Заметим, что наибольший ненулевой минор имеет размерность 3.
51
Заметим, что
ран матрицы самой системы равен 2 – это означает, что наша система не имеет решения, т.к. ранг расширенной матрицы больше ранга матрицы системы.
