геометрия
Поверхности второго порядка
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика. Поточная практика 7.5. Аналитическая геометрия. Поверхности второго порядка презентация
Содержание
- 2. Математика УГТУ-УПИ 2007г. М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко,
- 3. Цель занятия: 1. Овладеть соответствующим математическим
- 4. Формируемые компетенции по ФГОС:
- 5. Поверхности второго порядка
- 6. Поверхности второго порядка 1.Теоретическая часть 2.Задачи 3.Решения задач Оглавление
- 7. Поверхности второго порядка
- 8. Поверхности второго порядка Задача №: Оглавление:
- 9. Поверхности второго порядка Решение задачи №: Оглавление:
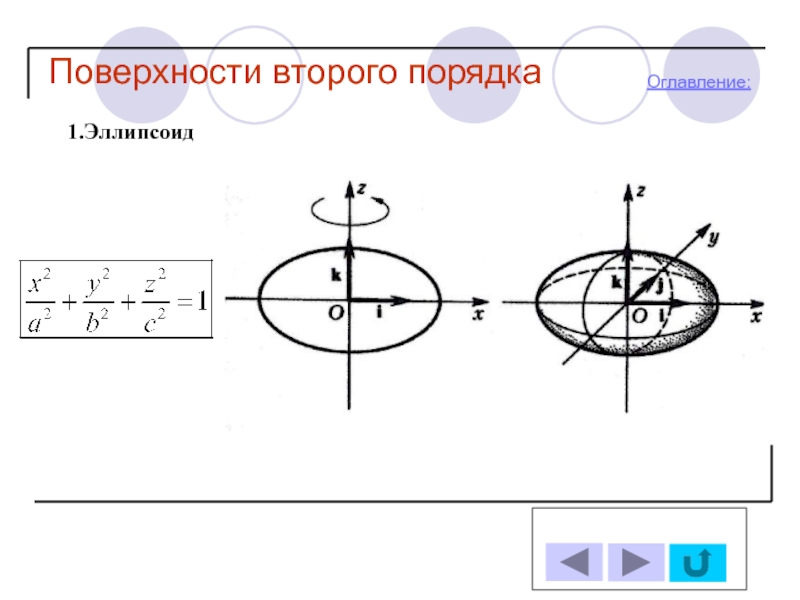
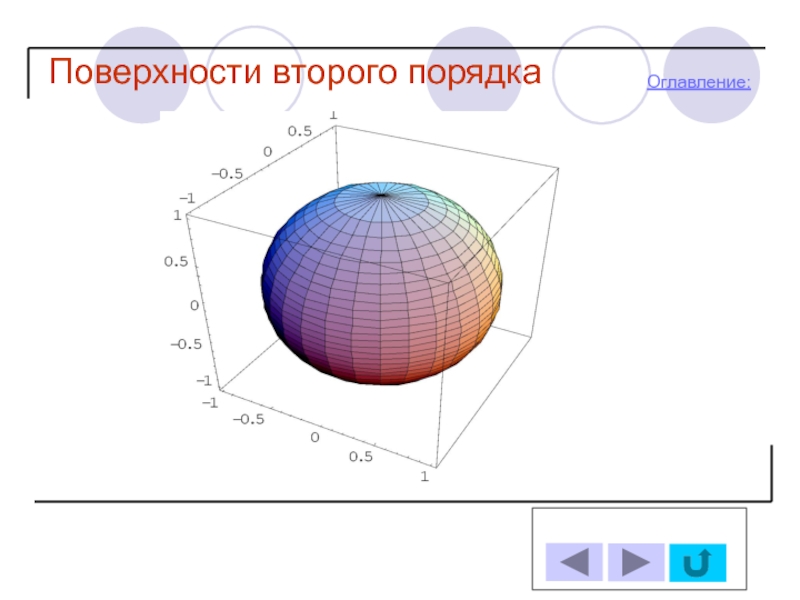
- 10. Поверхности второго порядка Оглавление: 1.Эллипсоид
- 11. Поверхности второго порядка Оглавление:
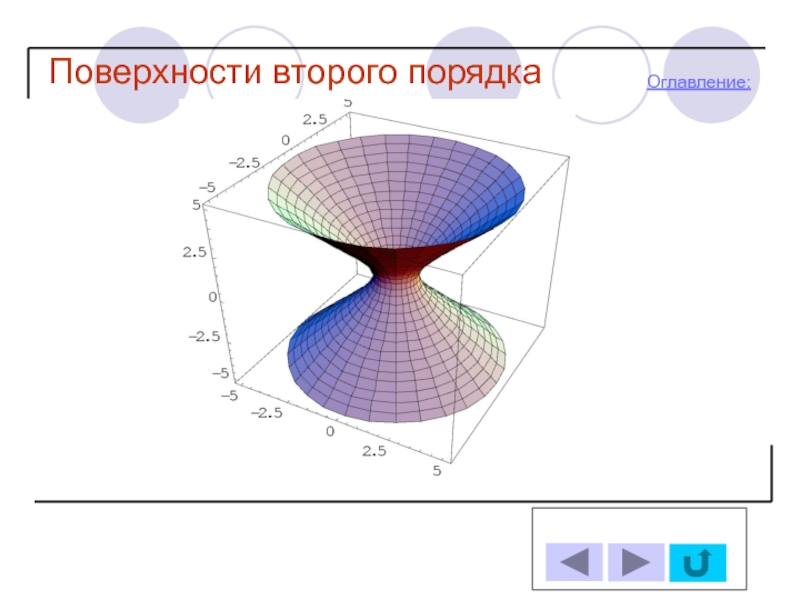
- 12. Поверхности второго порядка Оглавление: 2.Гиперболоиды Однополостный гиперболоид
- 13. Поверхности второго порядка Оглавление:
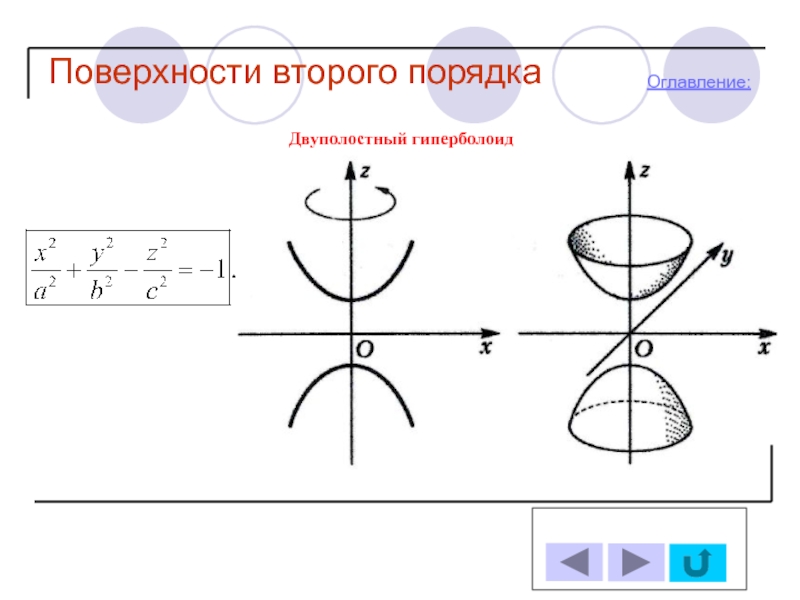
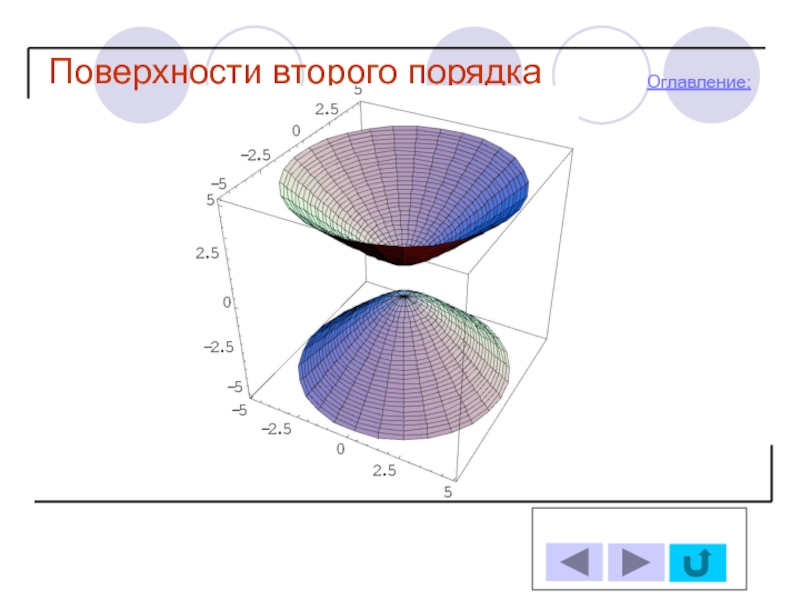
- 14. Поверхности второго порядка Оглавление: Двуполостный гиперболоид
- 15. Поверхности второго порядка Оглавление:
- 16. Поверхности второго порядка Оглавление: 3.Конус
- 17. Поверхности второго порядка Оглавление:
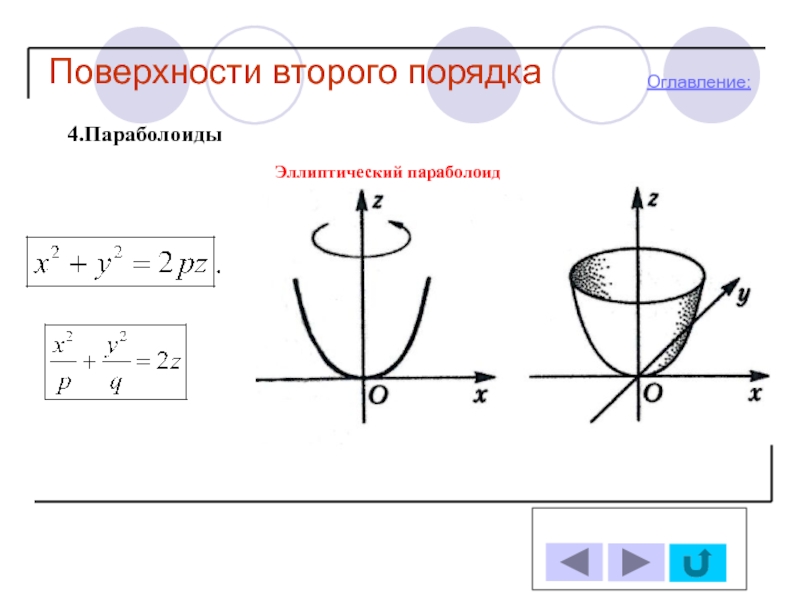
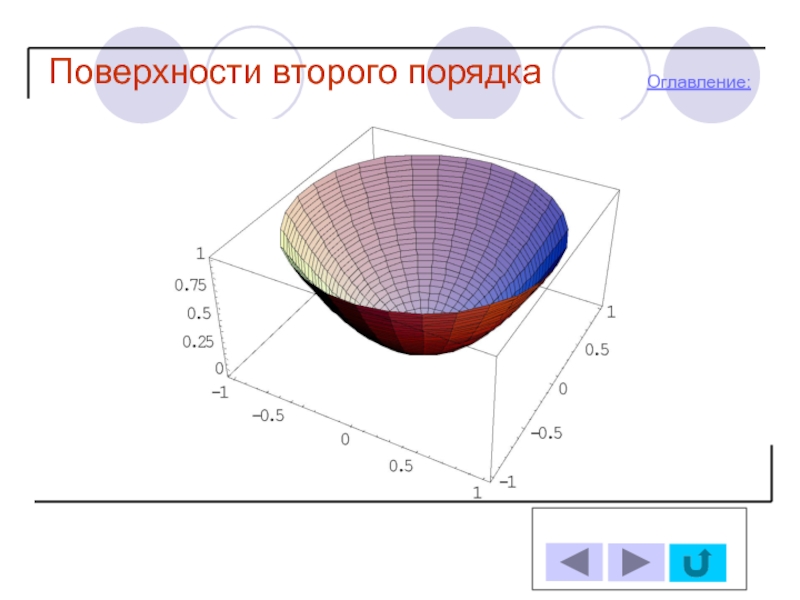
- 18. Поверхности второго порядка Оглавление: 4.Параболоиды Эллиптический параболоид
- 19. Поверхности второго порядка Оглавление:
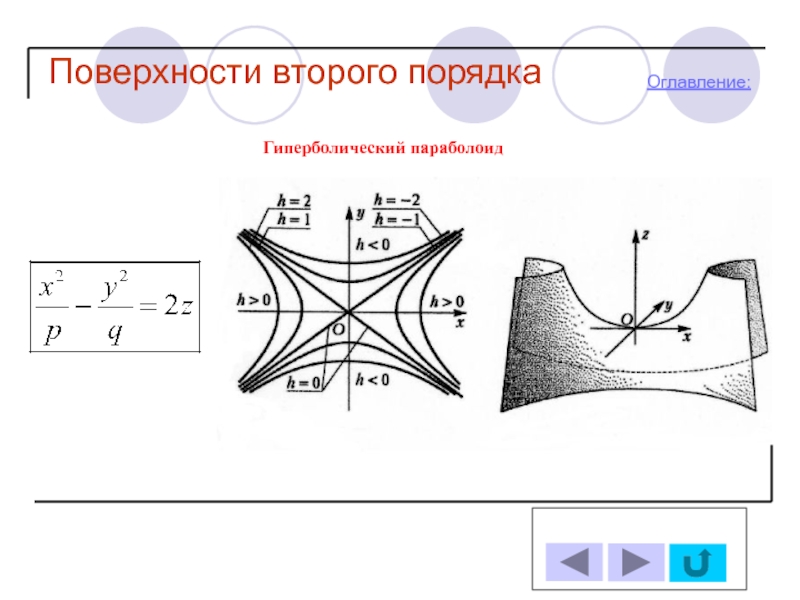
- 20. Поверхности второго порядка Оглавление: Гиперболический параболоид
- 21. Поверхности второго порядка
- 22. Поверхности второго порядка
- 23. Поверхности второго порядка Оглавление: параболический
- 24. Поверхности второго порядка Оглавление: 6.Пары плоскостей пара пересекающихся плоскостей
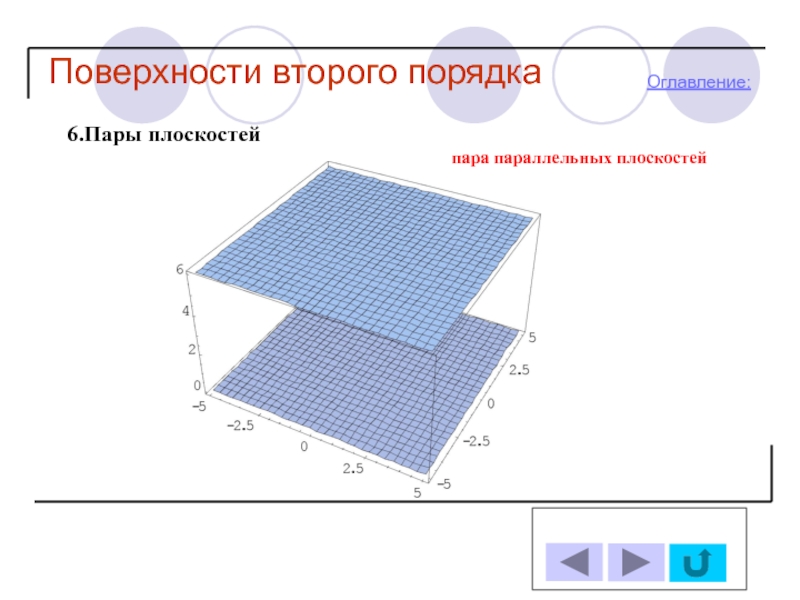
- 25. Поверхности второго порядка Оглавление: 6.Пары плоскостей пара параллельных плоскостей
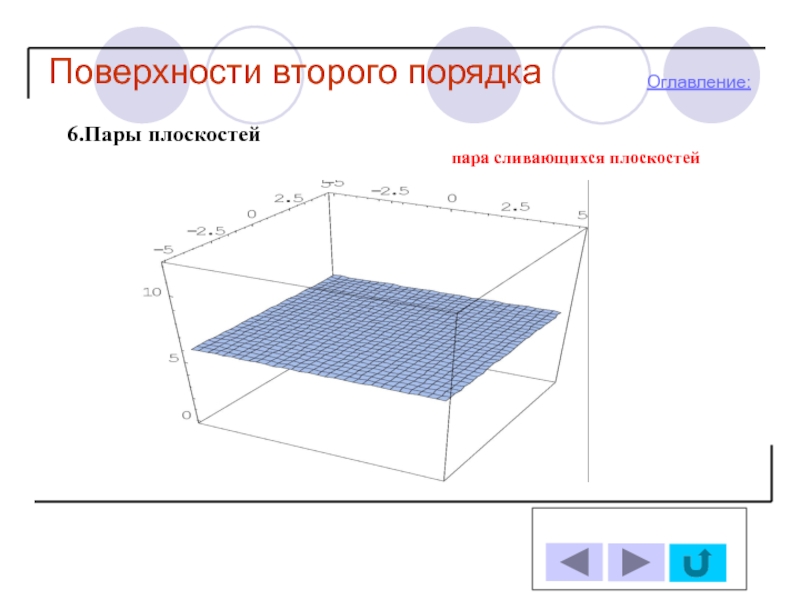
- 26. Поверхности второго порядка Оглавление: 6.Пары плоскостей пара сливающихся плоскостей
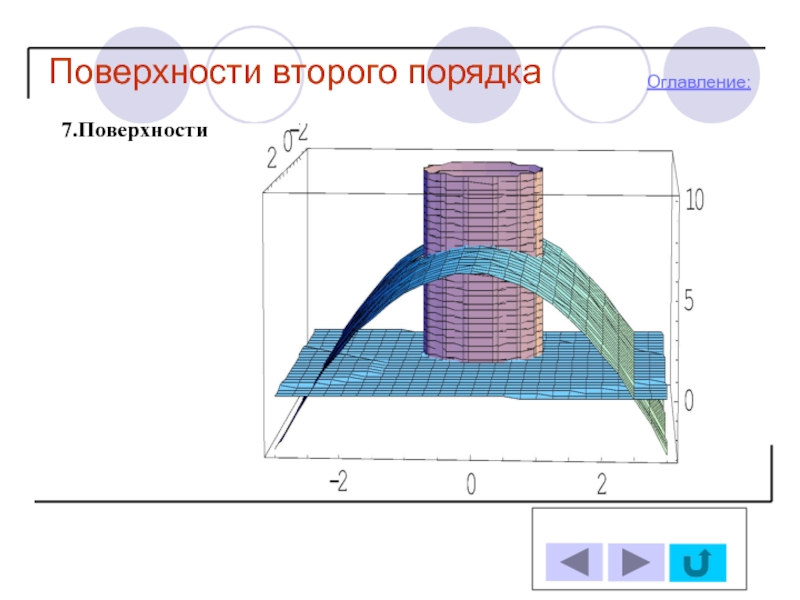
- 27. Поверхности второго порядка Оглавление: 7.Поверхности
- 28. Поверхности второго порядка Оглавление: 7.Поверхности
- 29. Поверхности второго порядка Оглавление: 7.Поверхности Броненосец
- 30. Поверхности второго порядка Оглавление: 7.Поверхности
- 31. Поверхности второго порядка Оглавление: 7.Поверхности
- 32. Задача 1 Ответ:
- 33. Ответ: Решение: Оглавление: Задача 2 Поверхности второго порядка Параболоид
- 34. Ответ: Решение: Оглавление: Задача 3 Поверхности второго порядка
- 35. Ответ: Решение:
- 36. Задача 5 Ответ: Решение: Оглавление: Поверхности второго порядка
- 37. Задача 6 Ответ:Нет Решение: Оглавление: Поверхности второго порядка
- 38. Задача 7 Ответ: Решение: Оглавление: Поверхности второго порядка
- 39. Задача 8 Ответ: Решение: Оглавление: Поверхности второго порядка
- 40. Задача 9 Ответ: Решение: Оглавление: Поверхности второго порядка
- 41. Задача 10 Ответ: Решение: Оглавление: Поверхности второго порядка
- 42. Ответ: Решение: Оглавление: Задача 11 Поверхности второго порядка
- 43. Ответ: Решение: Оглавление: Задача 12 Поверхности второго порядка
- 44. Ответ: Решение: Оглавление:
- 45. Решение задачи 1 Ответ: Оглавление: Поверхности второго порядка Двуполостный гиперболоид
- 46. Решение задачи 2 Ответ: Оглавление: Поверхности второго порядка Параболоид
- 47. Решение задачи 3 Ответ: Оглавление: Поверхности второго порядка
- 48. Решение задачи 4 Ответ: Оглавление: Поверхности второго порядка
- 49. Решение задачи 5 Ответ: Оглавление: Поверхности второго порядка
- 50. Решение задачи 6 Ответ: Нет Оглавление: Поверхности второго порядка
- 51. Решение задачи 7 Ответ: Оглавление: Поверхности второго порядка
- 52. Решение задачи 8 Ответ: Оглавление: Поверхности второго порядка
- 53. Решение задачи 9 Ответ: Оглавление: Поверхности второго порядка
- 54. Решение задачи 10 Ответ: Оглавление: Поверхности второго порядка
- 55. Решение задачи 11 Ответ: Оглавление: Поверхности второго порядка
- 56. Поверхности второго порядка Решение задачи 12 Ответ: Оглавление:
- 57. Поверхности второго порядка Решение задачи 12 Ответ: Оглавление:
- 58. Решение задачи 13 Ответ: Оглавление: Поверхности второго порядка Однополостный гиперболоид вращения
- 59. Решение задачи 13 Ответ: Оглавление: Поверхности второго порядка Однополостный гиперболоид вращения
- 60. В результате студент должен уметь строить поверхности второго порядка по их параллельным сечениям.
- 61. Перечень источников, список дополнительной литературы по
Слайд 2Математика
УГТУ-УПИ
2007г.
М.А.Вигура, О.А.Кеда, А.Ф.Рыбалко,
Н.М.Рыбалко, А.Б.Соболев
Поточная практика 7.5
Аналитическая
Слайд 3Цель занятия: 1. Овладеть соответствующим математическим аппаратом для дальнейшего изучения курса математики,
демонстрировать и использовать математические методы в ходе изучения специальных дисциплин для будущей профессиональной деятельности.
2. Запомнить канонические уравнения поверхностей и демонстрировать способность изобразить эллипсоид, гиперболоиды и параболоиды по их сечениям.
Слайд 7Поверхности второго порядка
Оглавление:
1. Эллипсоид
2. Гиперболоиды
-Однополостный гиперболоид
-Двуполостный гиперболоид
3. Конус
4. Параболоиды
-Эллиптический параболоид
-Гиперболический параболоид
5.
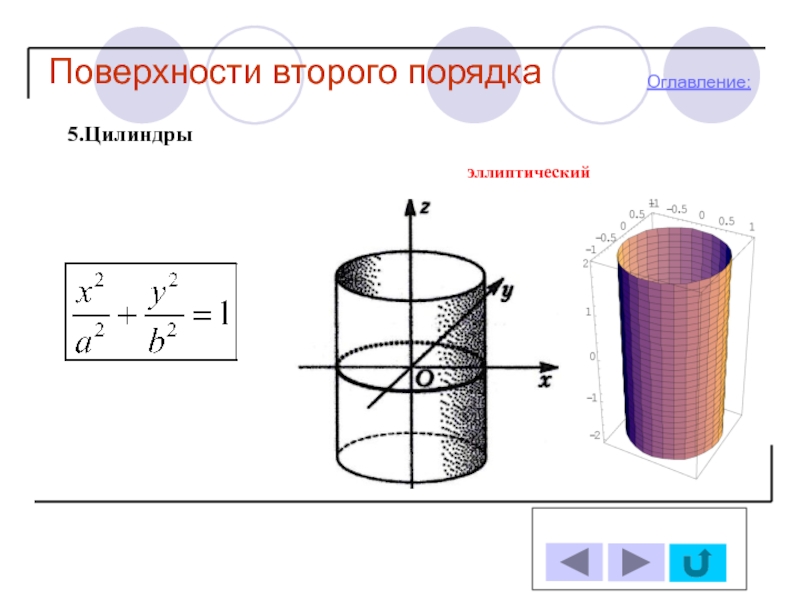
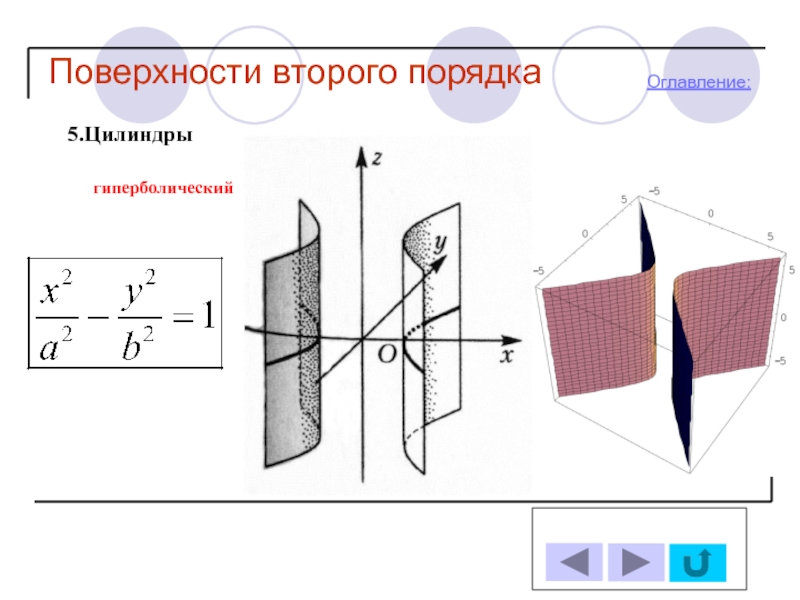
Цилиндры
-Эллиптический
-Гиперболический
-Параболический
6. Пары плоскостей
-пересекающихся
-параллельных
-сливающихся
7.Поверхности
-Эллиптический
-Гиперболический
-Параболический
6. Пары плоскостей
-пересекающихся
-параллельных
-сливающихся
7.Поверхности
Слайд 44Ответ:
Решение:
Оглавление:
Задача 13
Поверхности второго порядка
Однополостный гиперболоид вращения
Слайд 58Решение задачи 13
Ответ:
Оглавление:
Поверхности второго порядка
Однополостный гиперболоид вращения
Слайд 59Решение задачи 13
Ответ:
Оглавление:
Поверхности второго порядка
Однополостный гиперболоид вращения
Слайд 60В результате студент должен уметь
строить поверхности второго порядка по их параллельным
сечениям.
Слайд 61Перечень источников,
список дополнительной литературы по теме.
1. Сборник задач по математике
для втузов: В 4 ч. Ч. 1: Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры / А. В. Ефимов, А. Ф. Каракулин, И. Б. Кожухов и др. / Под ред. А. В. Ефимова, А. С. Поспелова. - 4-е изд., перераб. и доп. - М.: Физматлит, 2003. - 288 с.: ил.; 21 см. - ISBN 5-940520-34-0.
2. Клетеник, Давид Викторович. Сборник задач по аналитической геометрии: Учеб. пособие для студентов вузов / Под ред. Н.В. Ефимова. - 15-е изд. - М.: Наука. Физматлит, 1998. - 223с. - ISBN 5-02-015080-0.
3. Данко, Павел Ефимович. Высшая математика в упражнениях и задачах: Учеб. пособие для вузов: В 2 ч. Ч. 1 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд. - М.: ОНИКС 21 век : Мир и образование, 2003. - 304с.: ил.; 22 см. - ISBN 5-329-00326-1.
4. Элементы аналитической геометрии и линейной алгебры: Сб. комплектов вариантов задач по курсу "Высшая математика". Ч. 1 / Урал. гос. техн. ин-т; Сост. О. А. Белослудцев, М. А. Вигура, Н. В. Кожевников, А. Ф. Рыбалко и др. ; Науч. ред. С. И. Машаров. - Екатеринбург: УГТУ, 1997. - 110 с. - ISBN 5-230-17046-8.
2. Клетеник, Давид Викторович. Сборник задач по аналитической геометрии: Учеб. пособие для студентов вузов / Под ред. Н.В. Ефимова. - 15-е изд. - М.: Наука. Физматлит, 1998. - 223с. - ISBN 5-02-015080-0.
3. Данко, Павел Ефимович. Высшая математика в упражнениях и задачах: Учеб. пособие для вузов: В 2 ч. Ч. 1 / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. - 6-е изд. - М.: ОНИКС 21 век : Мир и образование, 2003. - 304с.: ил.; 22 см. - ISBN 5-329-00326-1.
4. Элементы аналитической геометрии и линейной алгебры: Сб. комплектов вариантов задач по курсу "Высшая математика". Ч. 1 / Урал. гос. техн. ин-т; Сост. О. А. Белослудцев, М. А. Вигура, Н. В. Кожевников, А. Ф. Рыбалко и др. ; Науч. ред. С. И. Машаров. - Екатеринбург: УГТУ, 1997. - 110 с. - ISBN 5-230-17046-8.