- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы. Сложение и вычитание векторов презентация
Содержание
- 1. Векторы. Сложение и вычитание векторов
- 2. Вектор — направленный отрезок
- 3. Коллинеарные векторы — ненулевые векторы,
- 4. Равные векторы Противоположные векторы сонаправленные
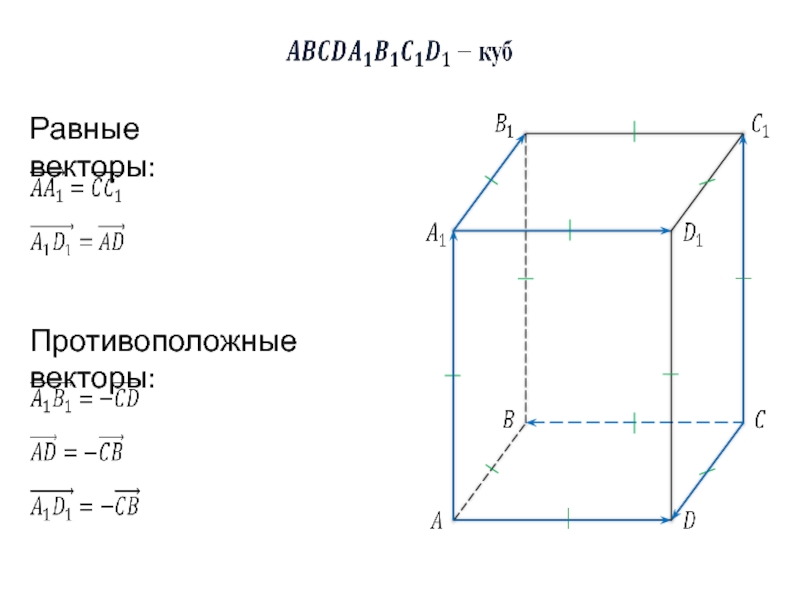
- 5. Равные векторы:
- 6. Равные векторы: Противоположные векторы:
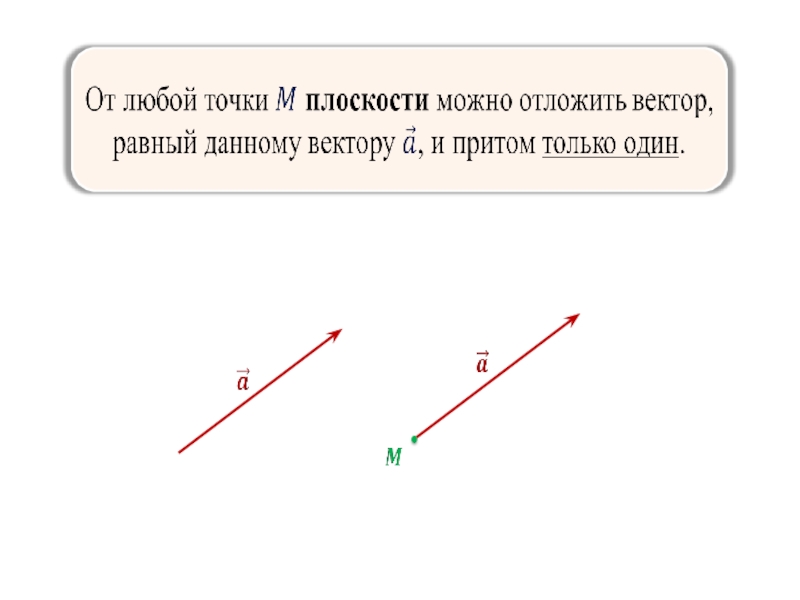
- 7.
- 8.
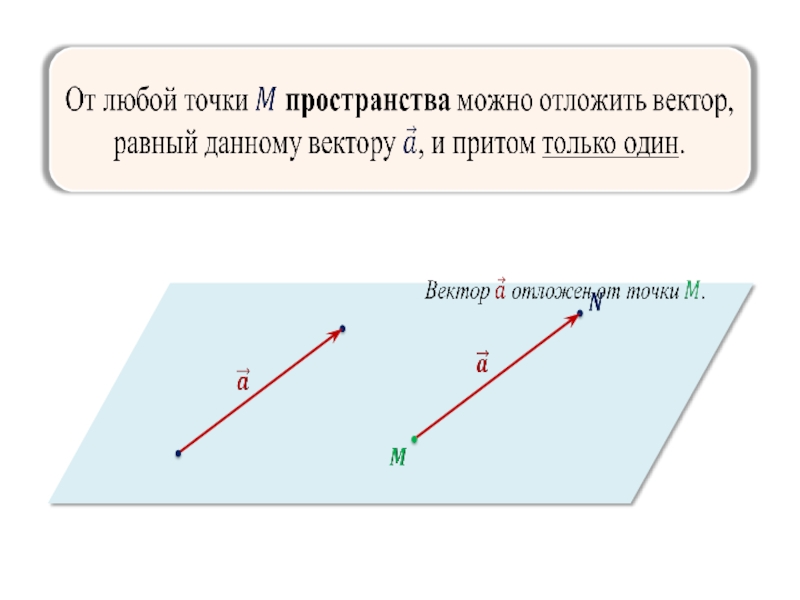
- 9. Сложение и вычитание векторов
- 10.
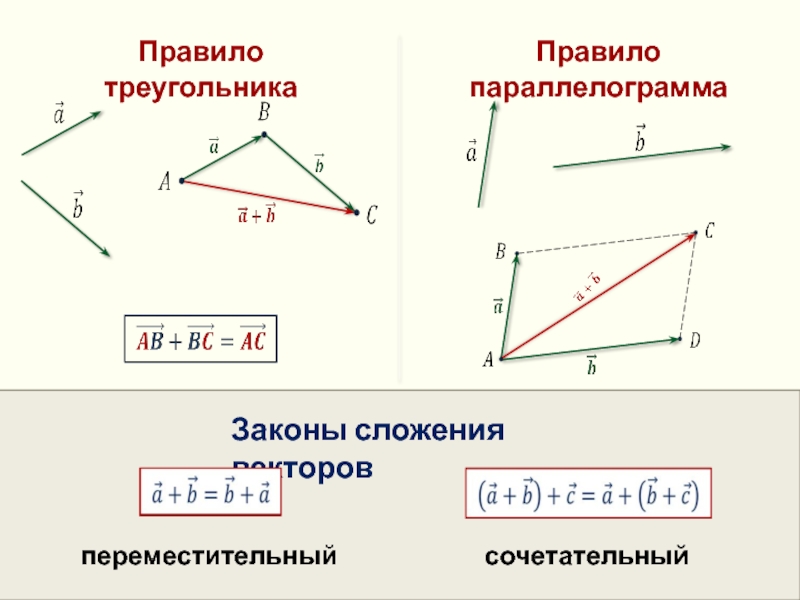
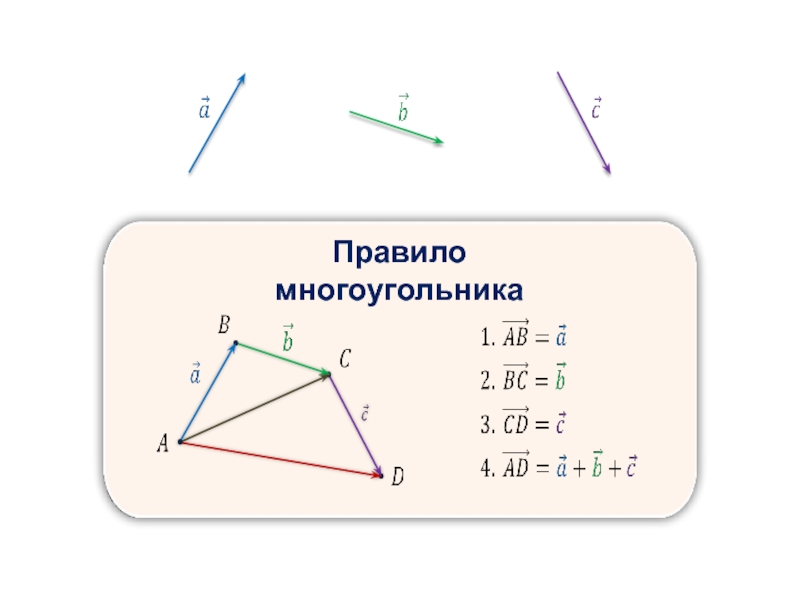
- 11. Правило треугольника
- 12. Правило треугольника
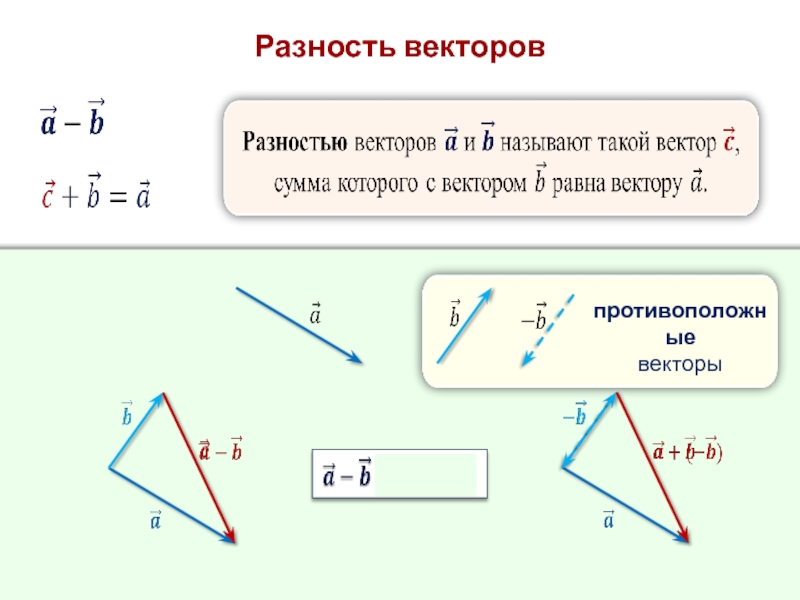
- 13. Разность векторов
- 14. Сумма нескольких векторов
- 15.
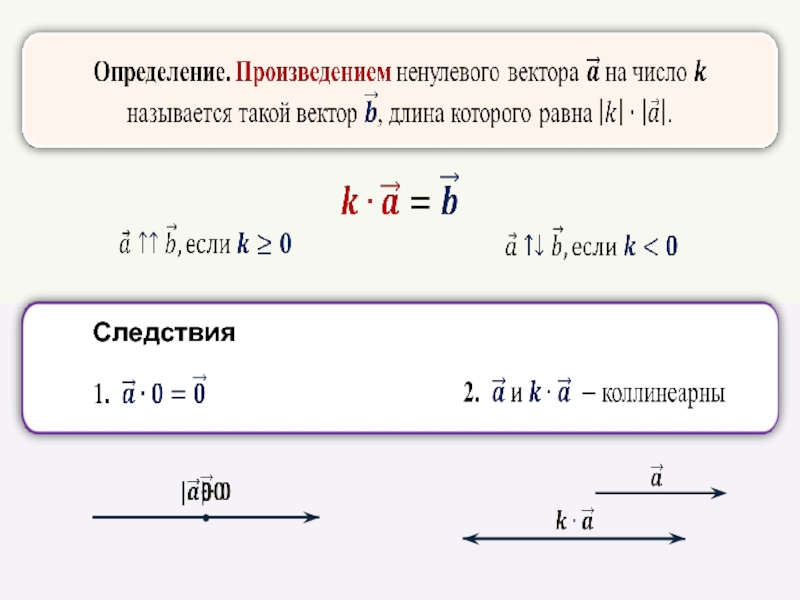
- 16. Умножение вектора на число
- 17.
- 18. Следствия
- 19. Свойства произведения
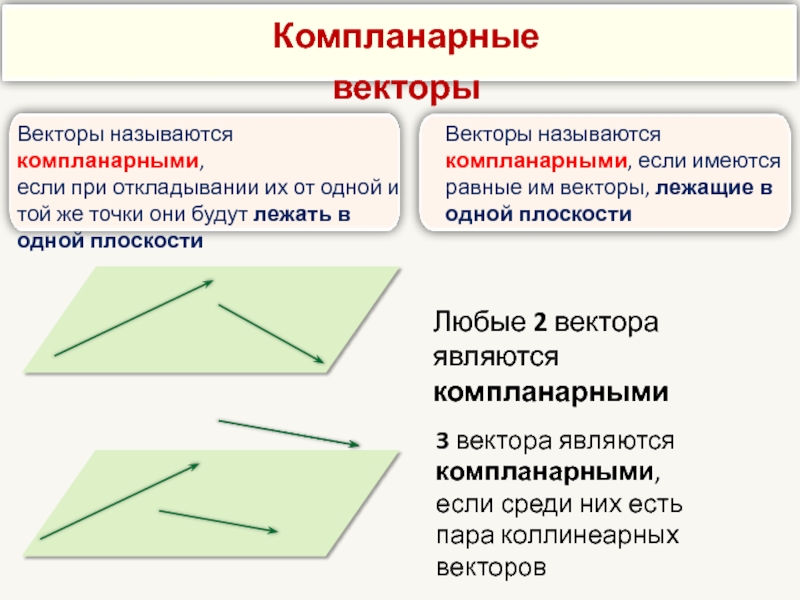
- 20. Векторы называются компланарными, если
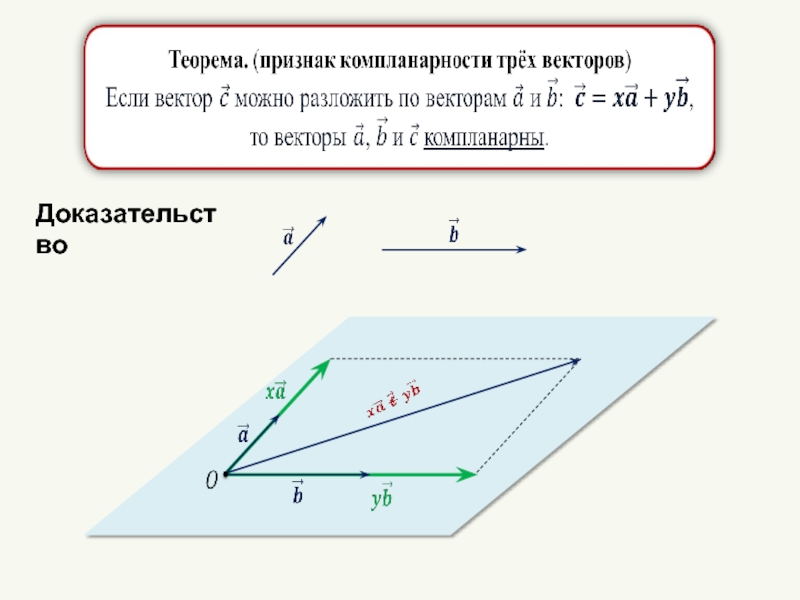
- 21. Доказательство
- 22. Доказательство.
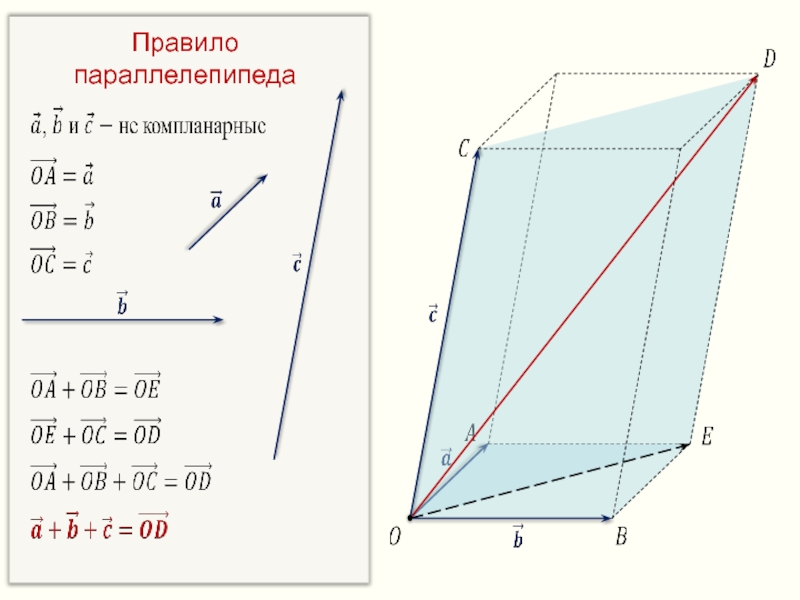
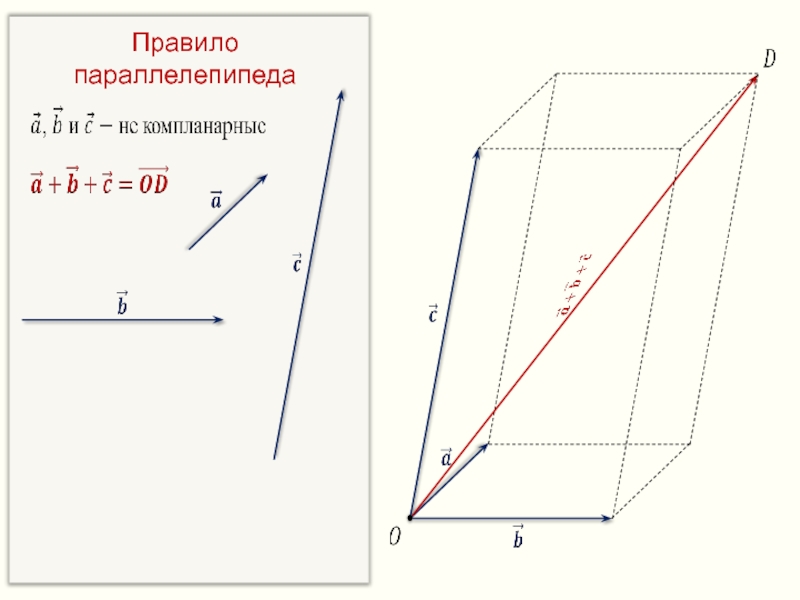
- 23. Правило параллелепипеда
- 24. Правило параллелепипеда
- 25. Правило параллелепипеда
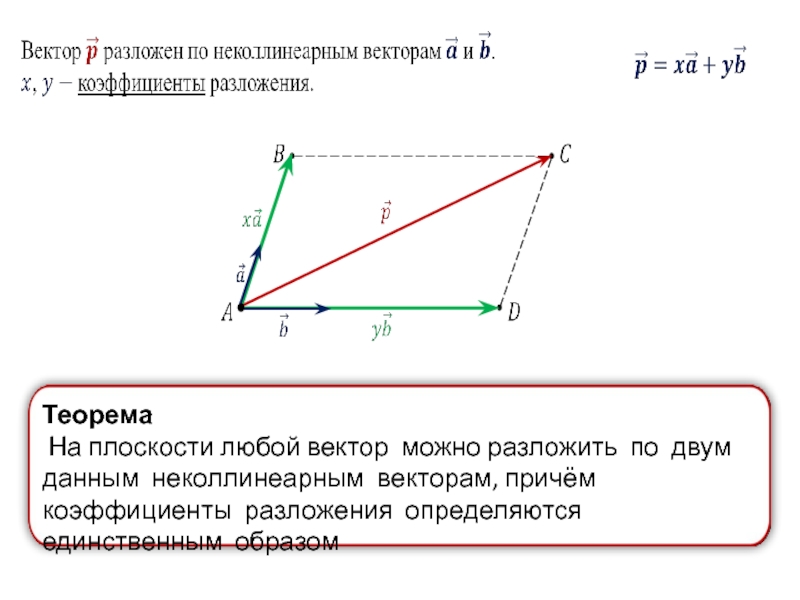
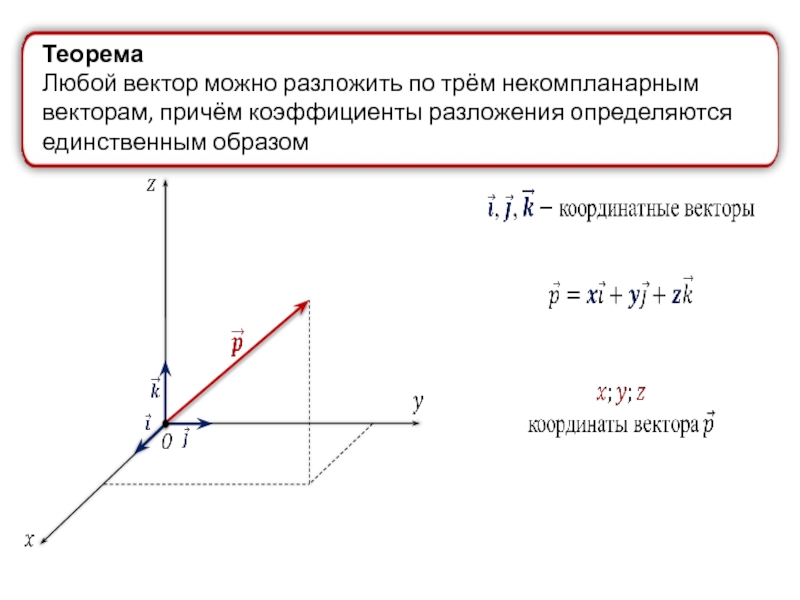
- 26. Разложение вектора по трём некомпланарным векторам
- 27.
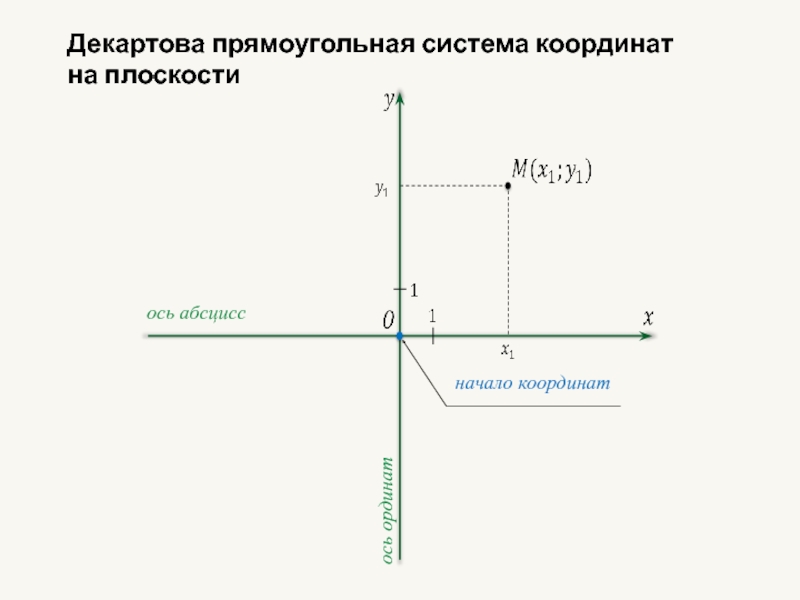
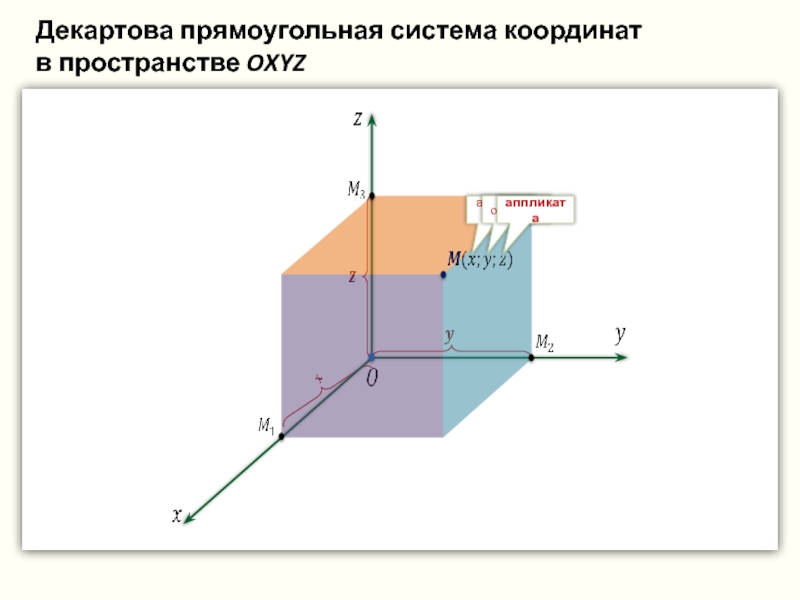
- 28. Прямоугольная система координат в пространстве
- 29. Рене Декарт 1596 - 1650 Французский философ, математик, механик, физик и физиолог Создатель аналитической геометрии и современной алгебраической символики
- 30.
- 31. ось координат ось
- 32. ось абсцисс ось
- 33.
- 34. положительная
- 35.
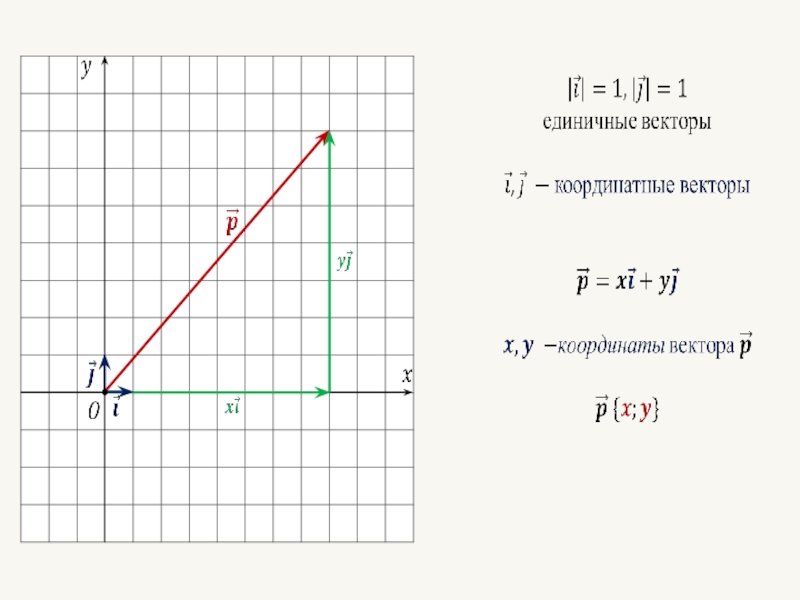
- 36. Координаты вектора
- 37.
- 38. Теорема Любой вектор можно разложить по
- 39. Пользуясь разложениями векторов по координатным векторам, записать
- 40.
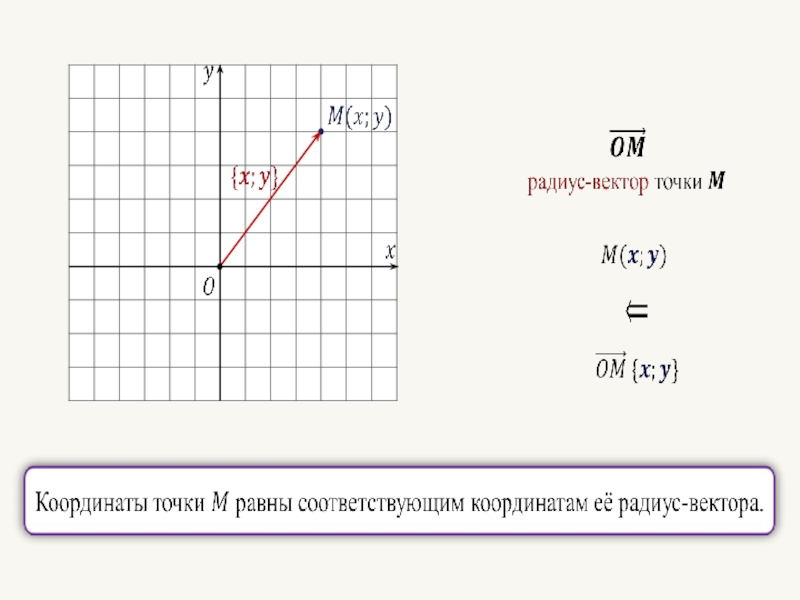
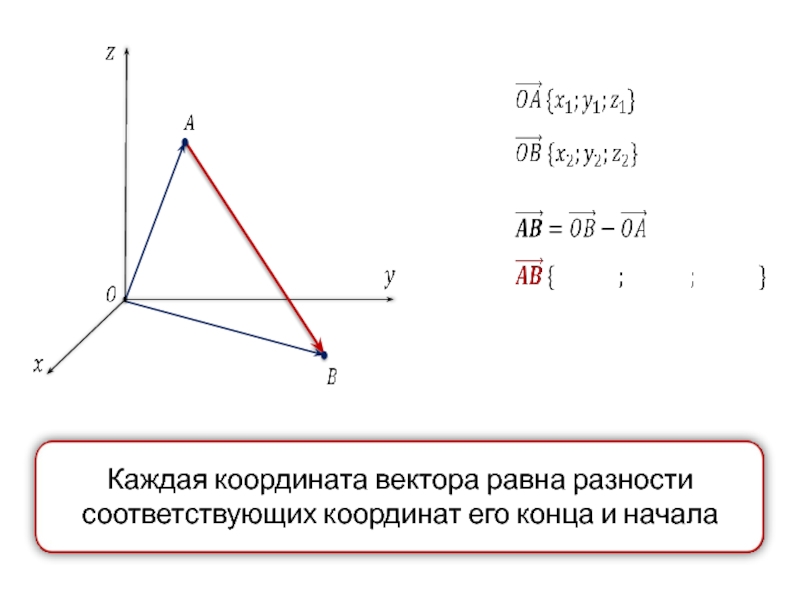
- 41. Связь между координатами векторов и координатами точек
- 42.
- 43.
- 44. Простейшие задачи в координатах
- 45. 1. Определение координат середины отрезка
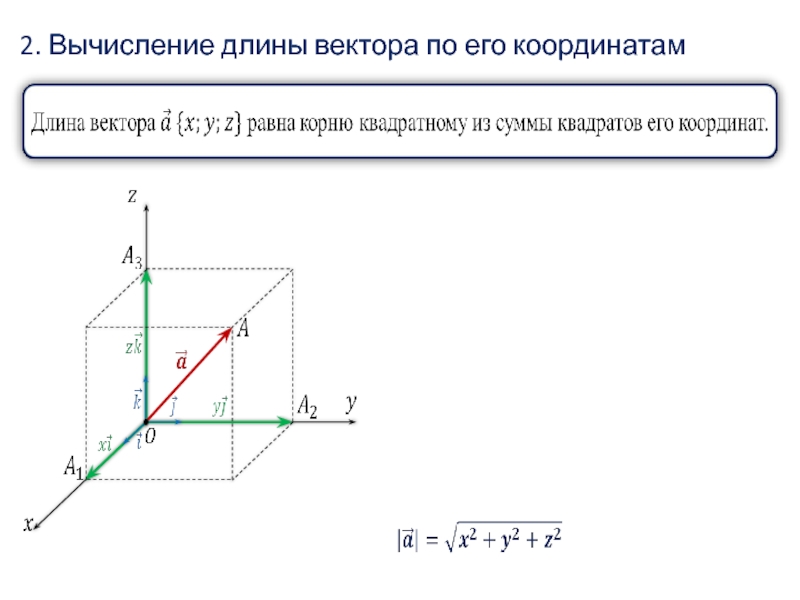
- 46. 2. Вычисление длины вектора по его координатам
- 47. Решение.
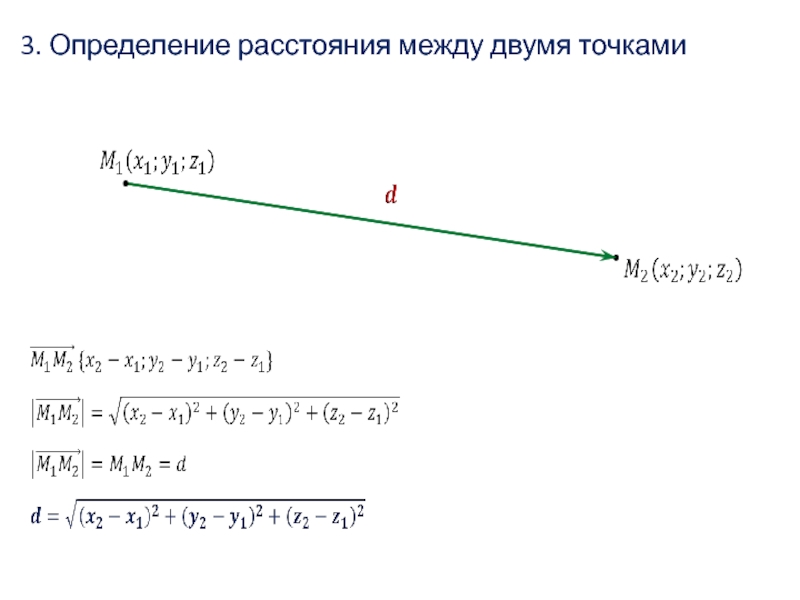
- 48. 3. Определение расстояния между двумя точками
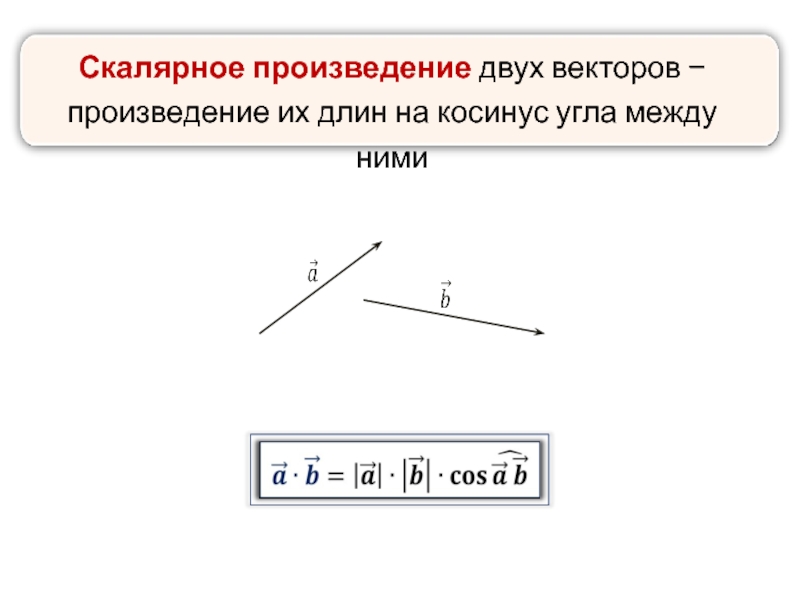
- 49. Скалярное произведение векторов
- 50. Скалярное произведение двух векторов − произведение их
- 51. Скалярное произведение векторов в координатах
- 52. Скалярное произведение векторов
- 53.
- 54. Свойства скалярного произведения векторов
Вектор — направленный отрезок нулевой вектор Длина ненулевого вектора равна длине отрезка Длина нулевого вектора равна 0
Слайд 2
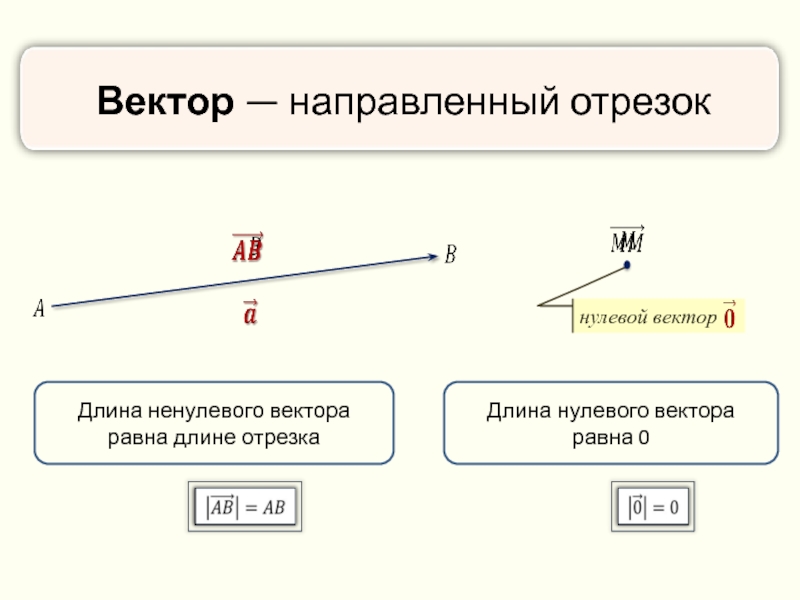
Вектор — направленный отрезок
нулевой вектор
Длина ненулевого вектора равна длине отрезка
Длина
нулевого вектора равна 0
Слайд 3
Коллинеарные векторы — ненулевые векторы,
лежащие на одной прямой или на параллельных
прямых
Нулевой вектор коллинеарен любому вектору
Коллинеарные векторы,
имеющие одинаковые направления,
называют сонаправленными
Коллинеарные векторы,
имеющие противоположные направления, называют противоположно направленными
Слайд 4
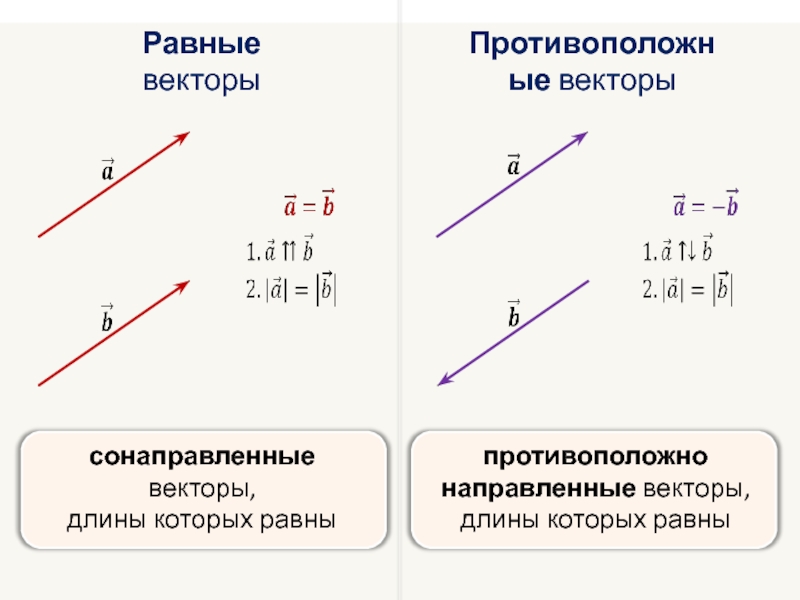
Равные векторы
Противоположные векторы
сонаправленные векторы,
длины которых равны
противоположно направленные векторы,
длины которых равны
Слайд 12
Правило треугольника
Правило параллелограмма
Законы сложения векторов
переместительный
сочетательный
Слайд 19
Свойства произведения вектора на число
позволяют выполнять преобразования в выражениях, содержащих суммы,
разности векторов и произведения векторов на числа, так же, как и в числовых выражениях
Слайд 20
Векторы называются компланарными,
если при откладывании их от одной и той же
точки они будут лежать в одной плоскости
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости
Любые 2 вектора являются компланарными
3 вектора являются компланарными,
если среди них есть
пара коллинеарных векторов
Слайд 27
Теорема
На плоскости любой вектор можно разложить по двум данным неколлинеарным
векторам, причём коэффициенты разложения определяются единственным образом
Слайд 29Рене Декарт
1596 - 1650
Французский философ,
математик, механик, физик и физиолог
Создатель аналитической геометрии и современной
алгебраической символики
Слайд 30
ось абсцисс
ось ординат
начало координат
Декартова прямоугольная система координат
на плоскости
Слайд 31
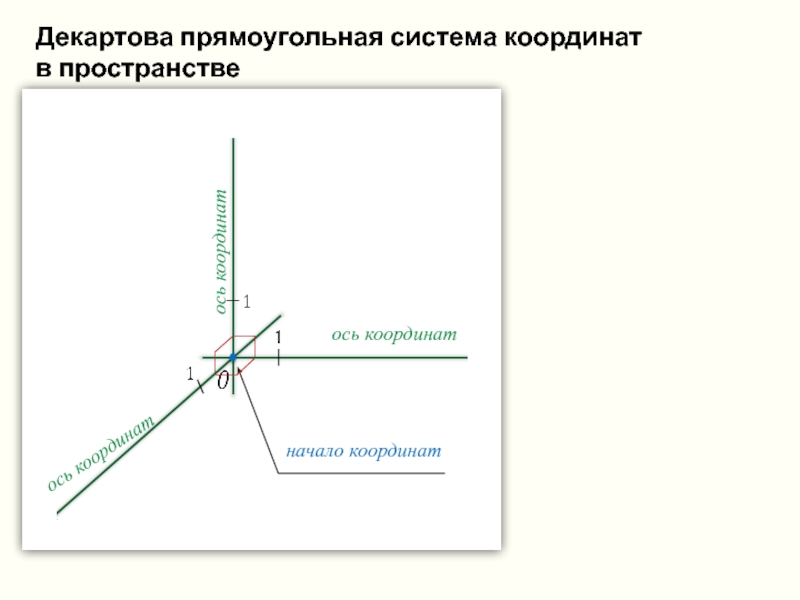
ось координат
ось координат
начало координат
ось координат
Декартова прямоугольная система координат
в пространстве
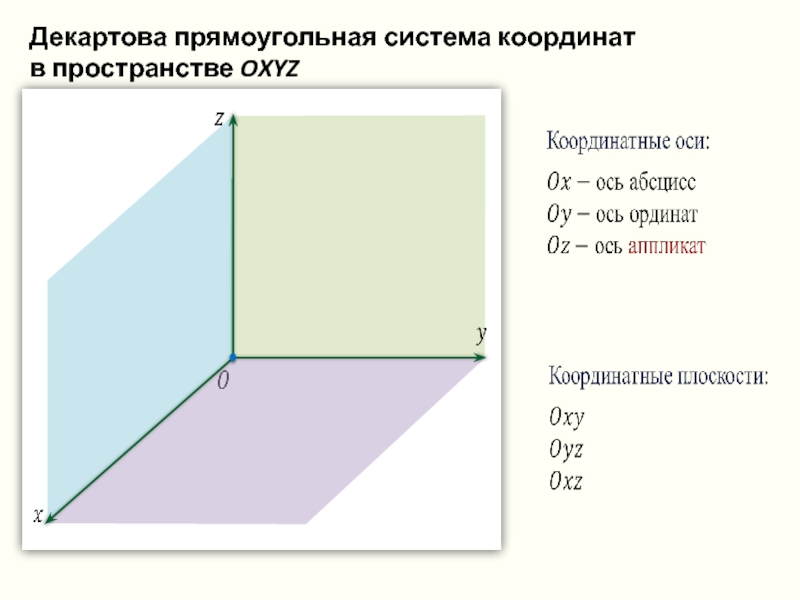
Слайд 32
ось абсцисс
ось ординат
ось аппликат
ось координат
ось координат
ось координат
Декартова прямоугольная система координат
в
пространстве OXYZ
Слайд 34
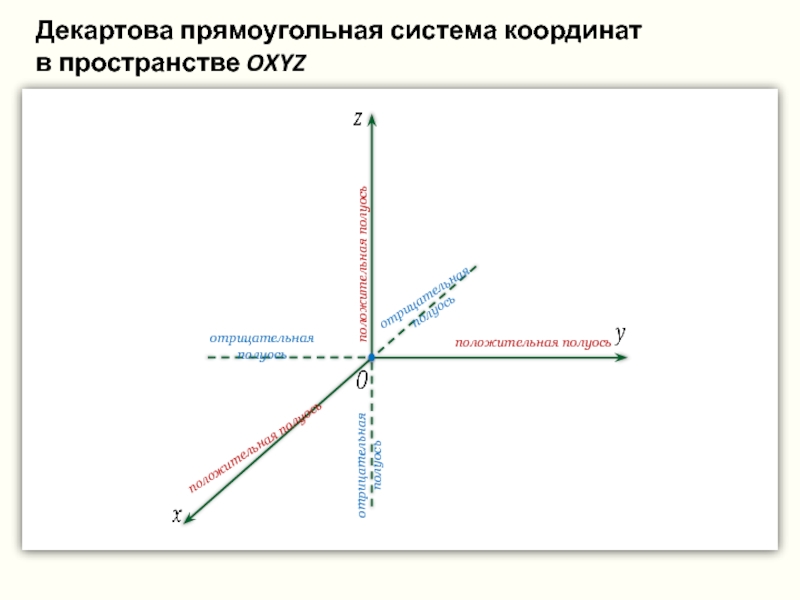
положительная полуось
положительная полуось
положительная полуось
отрицательная
полуось
отрицательная
полуось
отрицательная
полуось
Декартова прямоугольная система координат
в пространстве OXYZ
Слайд 38Теорема
Любой вектор можно разложить по трём некомпланарным векторам, причём коэффициенты
разложения определяются единственным образом
Слайд 39Пользуясь разложениями векторов по координатным векторам, записать их координаты
Пользуясь координатами векторов,
запишем их разложения по координатным векторам
Слайд 40
Позволяют определять
координаты любого
вектора,
представленного в виде алгебраической суммы
данных векторов
с известными
координатами
Слайд 45
1. Определение координат середины отрезка
Каждая координата середины отрезка равна полусумме
соответствующих координат
его концов
