Биостатистика
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Биостатистика. Сравнение выборок презентация
Содержание
- 1. Биостатистика. Сравнение выборок
- 2. Сравнение средних Самая первая и основная
- 3. Сравнение средних На прошлом занятии мы
- 4. Сравнение средних Распределение Стьюдента очень похоже
- 5. Сравнение средних Сравнение выборочного среднего
- 6. Упражняемся … 15 октября 2011 г.
- 7. Сравнение средних в случае зависимых выборок
- 8. Сравнение средних При сравнении средних двух
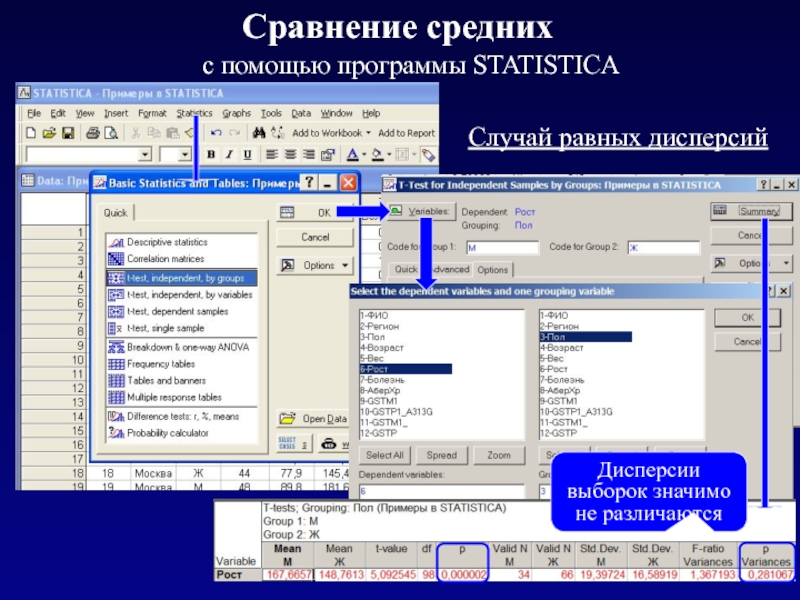
- 9. Сравнение средних c помощью программы STATISTICA Случай равных дисперсий
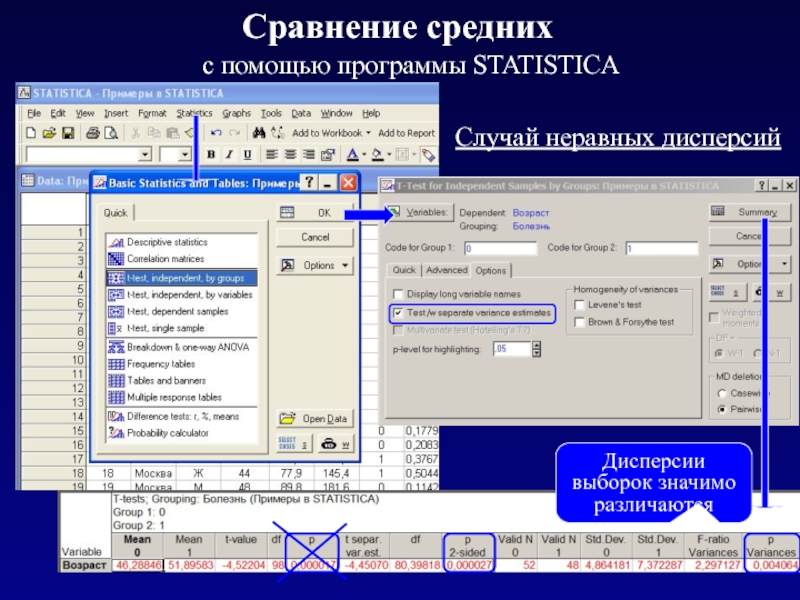
- 10. Сравнение средних c помощью программы STATISTICA
- 11. Сравнение дисперсий Р. Фишер построил критерий
- 12. Рассмотрим набор k выборок: Дисперсионный анализ (ANOVA)
- 13. Дисперсионный анализ (ANOVA) – сравнение нескольких выборок:
- 14. Дисперсионный анализ (ANOVA) – сравнение нескольких выборок:
- 15. Дисперсионный анализ (ANOVA) – сравнение нескольких выборок:
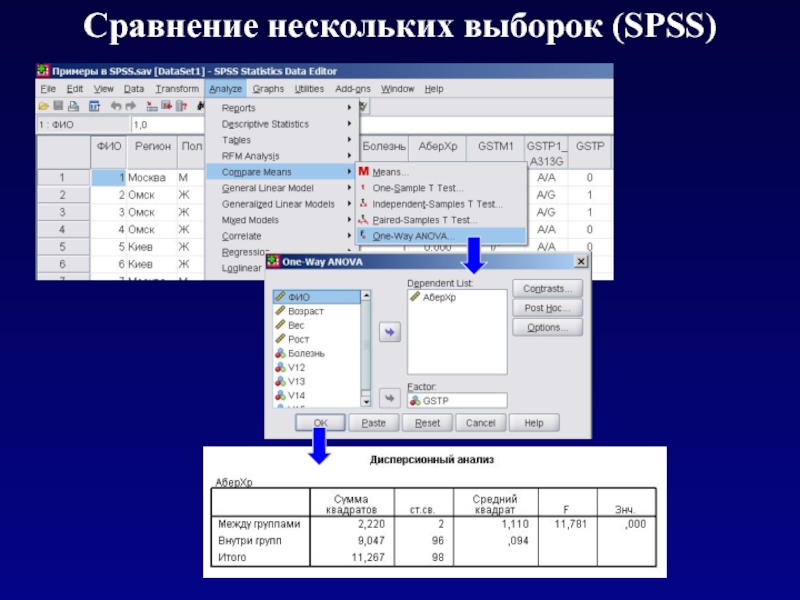
- 16. Сравнение нескольких выборок (SPSS)
- 17. Сравнение нескольких выборок (STATISTICA) Для нашей
- 18. Сравнение нескольких выборок (STATISTICA) Для нашей
- 19. Важное предупреждение В противном случае можно получить
- 20. Ранговые статистики Данные Ранги =ТТЕСТ(массив1; массив2; 2;
- 21. Ранговые критерии =БИНОМРАСП(1;8;0,5;1) 1 минус из 8
- 22. Ранговые критерии Для сравнения 2 независимых выборок
- 23. Проверяем нормальность … Строим гистограммы распределений аберраций
- 24. Непараметрический тест Манна – Уитни «Ненормальность» распределений не замедлила сказаться!
- 25. Тест Крускала - Уоллиса Для непараметрических тестов
- 26. Что значит «незначимо»? Допустим мы не обнаружили
- 27. Что значит «незначимо»? ⇒ Мощность всего
- 28. Поговорим о нормальном распределении Это
- 29. Почему нормальное распределение встречается на каждом шагу?
- 30. Пока мы говорили о сравнениях количественных признаков
- 31. Качественные признаки Будет правильно, если вы
- 32. Критерий χ2 Вычисляется сумма В 1900
- 33. Критерий χ2 Распределение χ2 при различных
- 34. Упражняемся … В выборке
- 35. Соответствие распределению Харди - Вайнберга Как
- 36. Для учебного файла определим частоты генотипов по локусу GSTP1 Упражняемся …
- 37. Вывод: нулевая гипотеза не отвергается. Частоты генотипов
- 38. Что означают серьезные отклонения от Харди
- 39. Критерий χ2 и таблицы сопряженности Тест
- 40. Критерий χ2 и таблицы сопряженности Как
- 41. Критерий χ2 и таблицы сопряженности Все это можно делать, используя STATISTICA
- 42. Критерий χ2 и таблицы сопряженности Это
- 43. Критерий χ2 и таблицы сопряженности Таблица
- 44. Критерий χ2: проверка однородности данных В
- 45. На сегодня это все Напоследок хочу посоветовать:
Слайд 1Институт общей генетики им. Н.И. Вавилова РАН
4. Сравнение выборок
Рубанович
Слайд 2Сравнение средних
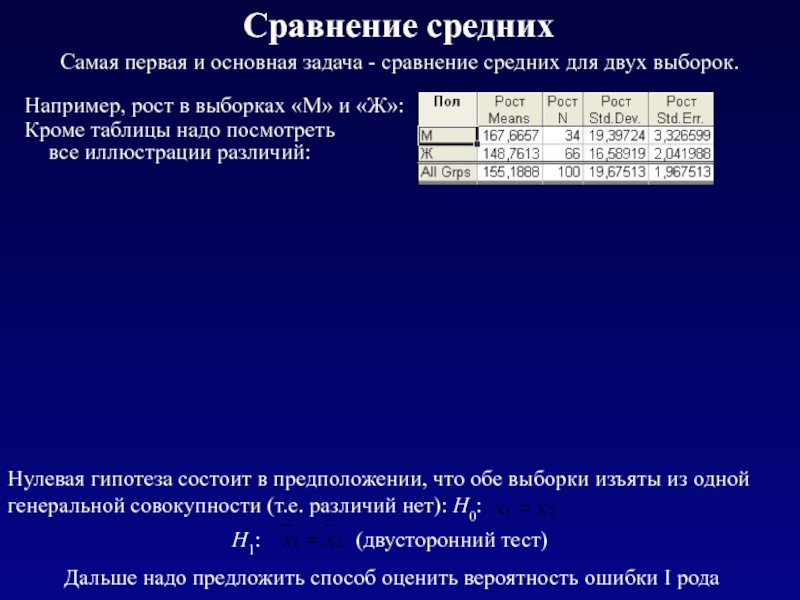
Самая первая и основная задача - сравнение средних для
Например, рост в выборках «М» и «Ж»:
Дальше надо предложить способ оценить вероятность ошибки I рода
Кроме таблицы надо посмотреть все иллюстрации различий:
Слайд 3Сравнение средних
На прошлом занятии мы рассмотрели достаточно универсальный способ построения
Есть надежда, что эта величина имеет нормальное распределение со средним 0 и дисперсией 1. Так оно и есть, но только при больших объемах выборок!
, т.е. разность средних, деленная
на стандартное отклонение этой разности.
Слайд 4Сравнение средних
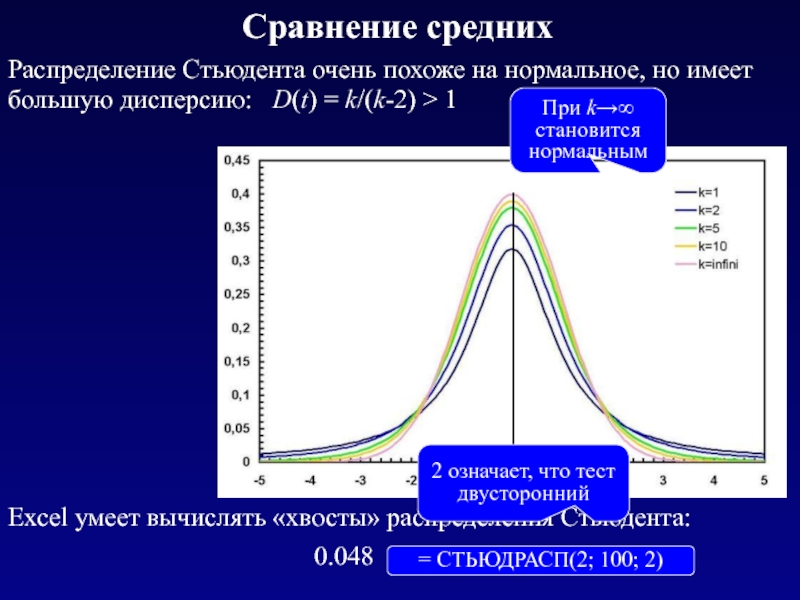
Распределение Стьюдента очень похоже на нормальное, но имеет большую
При k→∞ становится нормальным
Excel умеет вычислять «хвосты» распределения Стьюдента:
= СТЬЮДРАСП(2; 100; 2)
2 означает, что тест двусторонний
0.048
Слайд 5Сравнение средних
Сравнение выборочного среднего с известным числом
Сравнение двух
Сравнение двух выборочных средних для независимых выборок
Для каждой особи проводят 2 однотипных замера:
- до и после приема лекарства,
- в этом году и в прошлом году и т.д.
3 варианта использования теста Стьюдента:
Слайд 6Упражняемся …
15 октября 2011 г. президент Д. Медведев сообщил, что
В этом месяце в районном морге побывало 100 клиентов, и получена другая оценка: 62±3 года. Отличается ли эта оценка от средней по стране?
= СТЬЮДРАСП((69-62)/3; 100-1; 2)
Р = 0.022
Вывод: нулевая гипотеза отвергается. Вероятность того, что при этом отвергли правильную нулевую гипотезу равна 0.022 (ошибка I рода). Выборка по данным районного морга не соответствует среднему по стране.
Различия статистически значимы.
2 означает, что тест двусторонний
Эта запись означает, что наша величина имеет распределение Стьюдента с n-1 степенями свободы
Никогда не пишите, что различия достоверны!
Достоверно это то, что происходит с вероятностью 1
В данном примере среднее для одной выборки сравнивалось с заранее известной величиной. Это так называемый одновыборочный тест
(мы это уже делали: помните 470 из 1000?)
Слайд 7Сравнение средних
в случае зависимых выборок
Это простой случай. Вычисляется t-статистика
и
Можно ни о чем этом не думать и использовать
=ТТЕСТ(массив1; массив2; 2; 1)
2 означает, что тест двусторонний
1 означает, что выборки зависимы
Для независимых выборок все несколько сложнее…
Слайд 8Сравнение средних
При сравнении средних двух независимых выборок возможны 2 ситуации:
σ1 = σ2 , т.е. изменчивость данных в обеих выборках одинакова
σ1 ≠ σ2 , т.е. изменчивость данных в выборках неодинакова, и эти различия статистически значимы. Тогда вычисляется объединенная дисперсия для двух выборок. Число степеней свободы тоже модифицируется.
В Excel это делается так:
=ТТЕСТ(массив1; массив2; 2; 2)
2 означает, что тест двусторонний
2 - σ1 = σ2
3 - σ1 ≠ σ2
Excel при этом не проверяет статистическую значимость σ1 ≠ σ2 .
Более адекватно в STATISTICA:
в случае независимых выборок
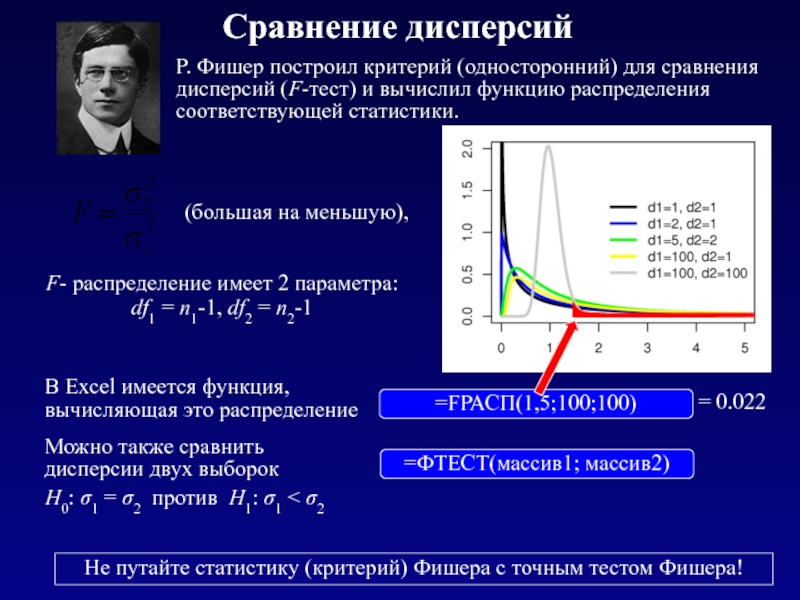
Слайд 11Сравнение дисперсий
Р. Фишер построил критерий (односторонний) для сравнения дисперсий (F-тест)
Не путайте статистику (критерий) Фишера с точным тестом Фишера!
=ФТЕСТ(массив1; массив2)
=FРАСП(1,5;100;100)
В Excel имеется функция, вычисляющая это распределение
Можно также сравнить дисперсии двух выборок
Н0: σ1 = σ2 против Н1: σ1 < σ2
F- распределение имеет 2 параметра: df1 = n1-1, df2 = n2-1
= 0.022
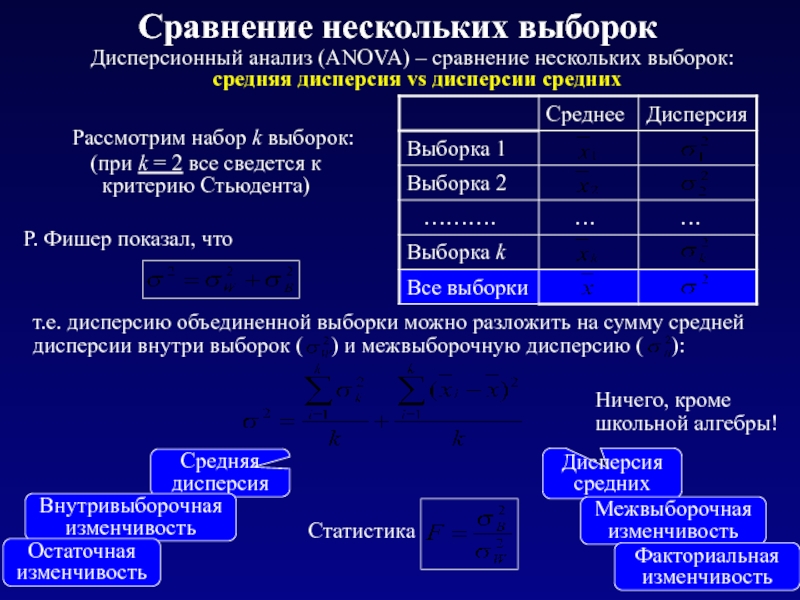
Слайд 12Рассмотрим набор k выборок:
Дисперсионный анализ (ANOVA) – сравнение нескольких выборок:
средняя дисперсия
Ничего, кроме школьной алгебры!
Средняя дисперсия
Дисперсия средних
Межвыборочная изменчивость
Внутривыборочная изменчивость
Факториальная изменчивость
Остаточная изменчивость
(при k = 2 все сведется к критерию Стьюдента)
Сравнение нескольких выборок
Слайд 13Дисперсионный анализ (ANOVA) – сравнение нескольких выборок:
средняя дисперсия vs дисперсии средних
Сравнение
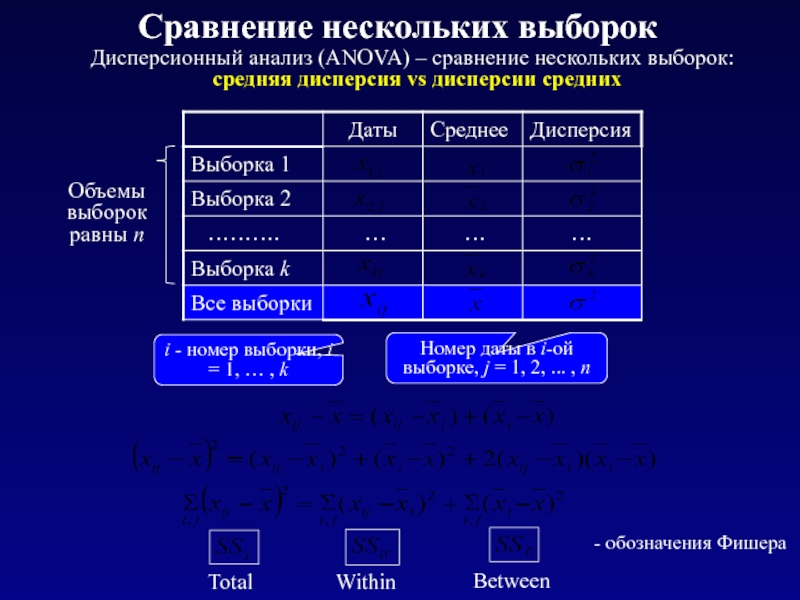
Слайд 14Дисперсионный анализ (ANOVA) – сравнение нескольких выборок:
средняя дисперсия vs дисперсии средних
-
Сравнение нескольких выборок
Слайд 15Дисперсионный анализ (ANOVA) – сравнение нескольких выборок:
средняя дисперсия vs дисперсии средних
Н0:
vs Н1: хотя бы одно среднее отличается
F-статистика не дает указаний на то, в какой выборке среднее больше! Это одновременное сравнение совокупности выборок.
«Разборки» со средними называются Post Hoc Tests
Табличка Фишера:
Сравнение нескольких выборок
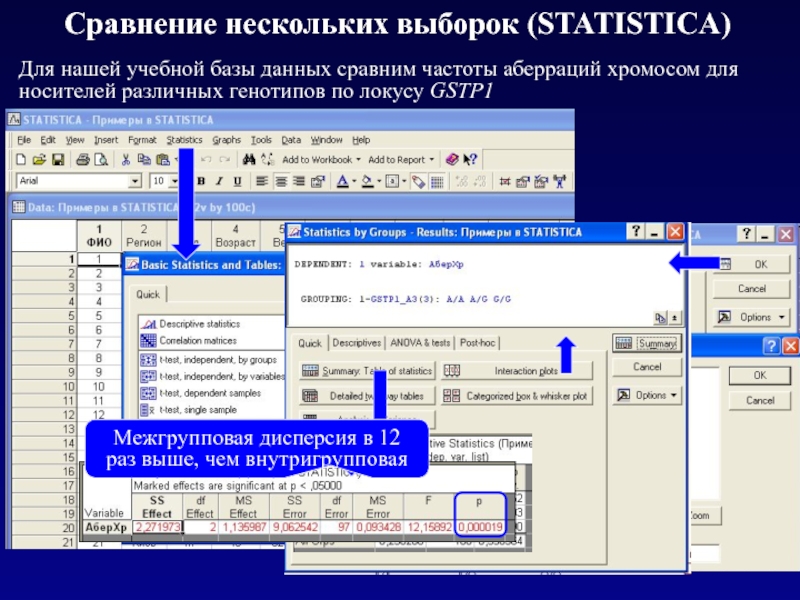
Слайд 17Сравнение нескольких выборок (STATISTICA)
Для нашей учебной базы данных сравним частоты
Межгрупповая дисперсия в 12 раз выше, чем внутригрупповая
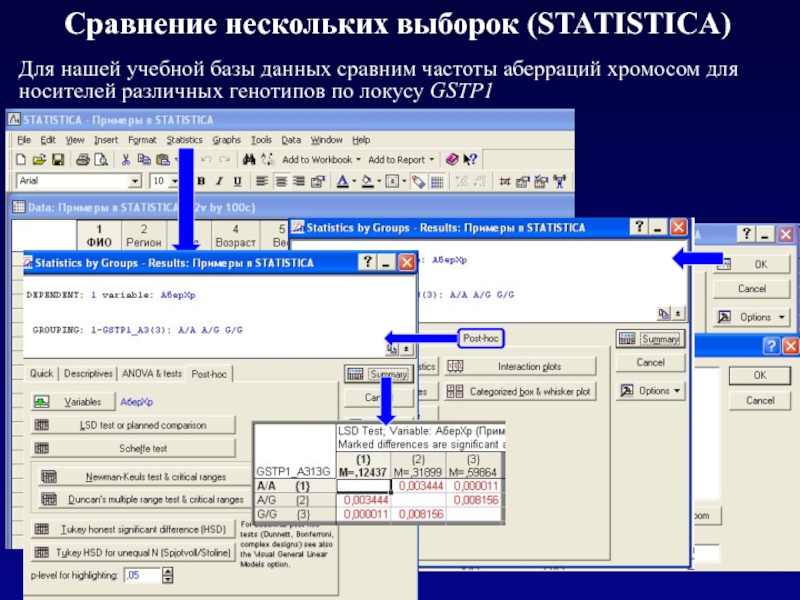
Слайд 18Сравнение нескольких выборок (STATISTICA)
Для нашей учебной базы данных сравним частоты
Слайд 19Важное предупреждение
В противном случае можно получить совершенно абсурдный результат:
В какой
=ТТЕСТ(массив1; массив2; 2; 3)
На этом примере видно, что в ряде случаев надо сравнивать не сами данные,
а их порядковые ранги (номера в последовательности)
Средние
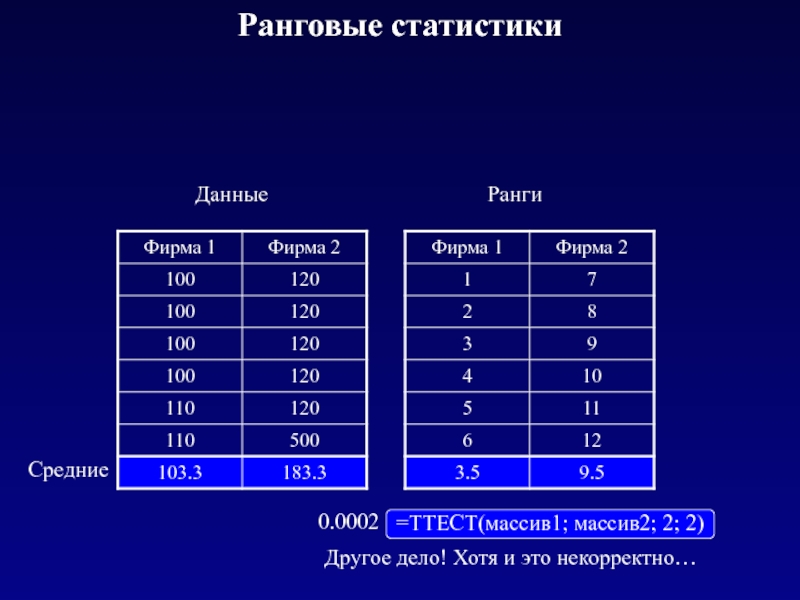
Слайд 20Ранговые статистики
Данные
Ранги
=ТТЕСТ(массив1; массив2; 2; 2)
0.0002
Другое дело! Хотя и это некорректно…
Средние
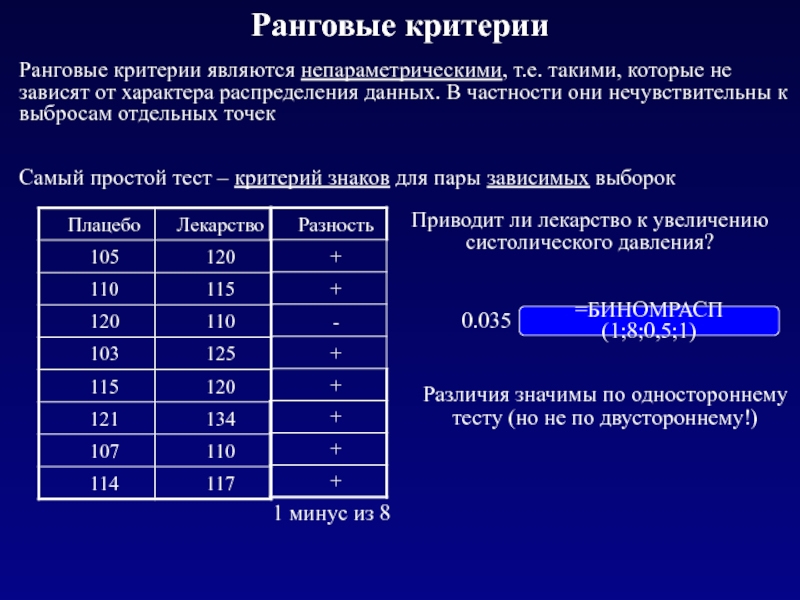
Слайд 21Ранговые критерии
=БИНОМРАСП(1;8;0,5;1)
1 минус из 8
Ранговые критерии являются непараметрическими, т.е. такими, которые
Самый простой тест – критерий знаков для пары зависимых выборок
0.035
Различия значимы по одностороннему тесту (но не по двустороннему!)
Приводит ли лекарство к увеличению систолического давления?
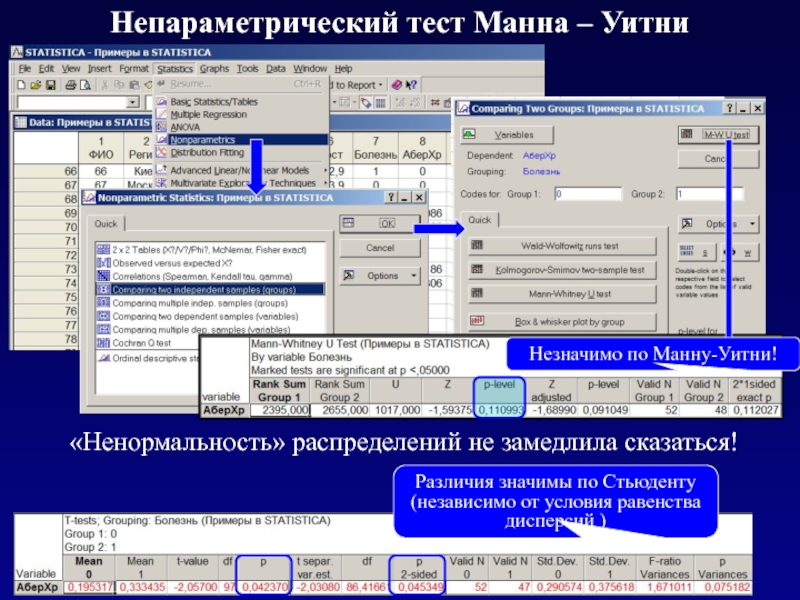
Слайд 22Ранговые критерии
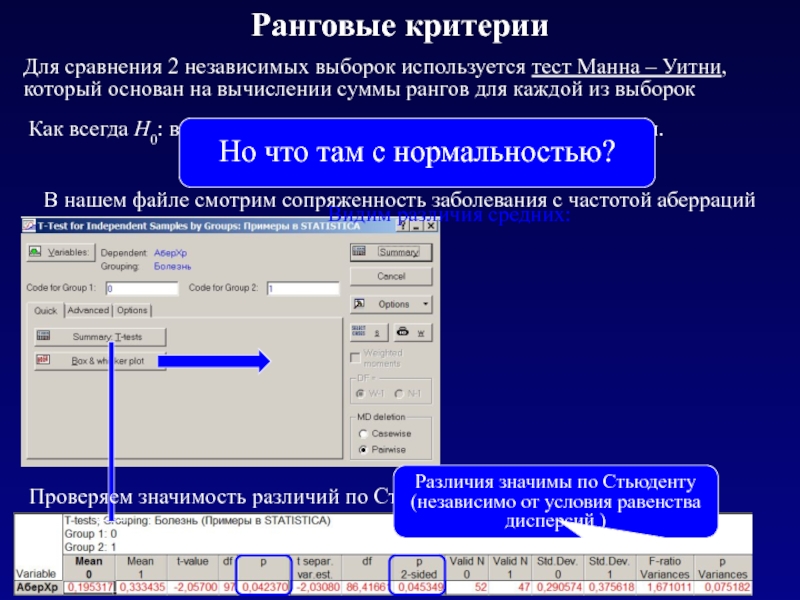
Для сравнения 2 независимых выборок используется тест Манна – Уитни,
который
Как всегда Н0: выборки взяты из одной генеральной совокупности.
Упражняемся …
В нашем файле смотрим сопряженность заболевания с частотой аберраций
Видим различия средних:
Проверяем значимость различий по Стьюденту:
Но что там с нормальностью?
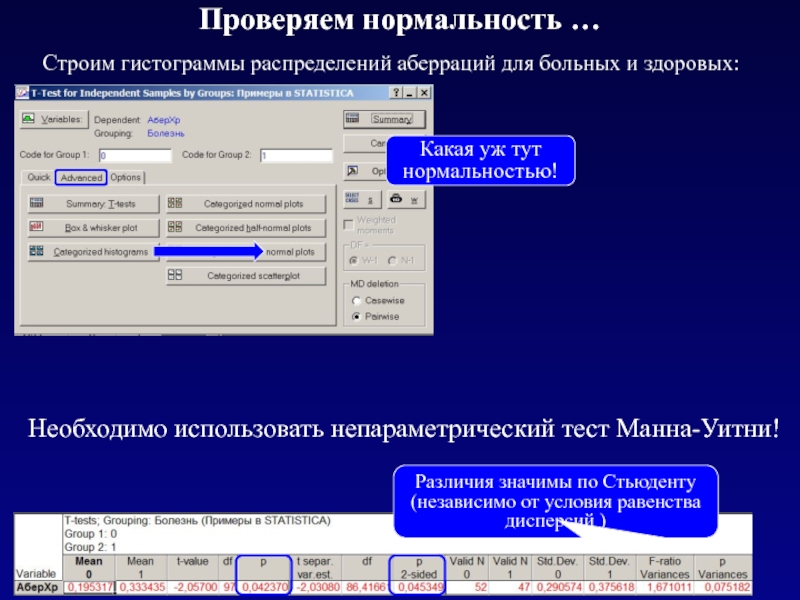
Слайд 23Проверяем нормальность …
Строим гистограммы распределений аберраций для больных и здоровых:
Необходимо использовать
Какая уж тут нормальностью!
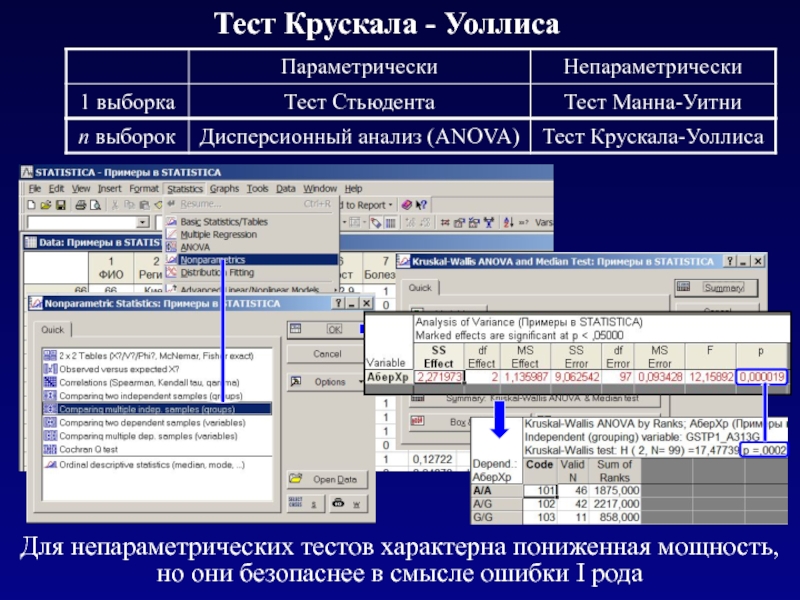
Слайд 25Тест Крускала - Уоллиса
Для непараметрических тестов характерна пониженная мощность, но они
Слайд 26Что значит «незначимо»?
Допустим мы не обнаружили статистическую значимость различий, о чем
НЕТ! Мы должны продемонстрировать, что объемы наших выборок достаточны, чтобы обнаружить эффект, если он существует.
Мощность (чувствительность) используемых тестов должна быть не ниже 80% (тогда упускаем не более 20% открытий)
Только в этом случае незначимые различия можно рассматривать как отрицательный результат
Слайд 27Что значит «незначимо»?
⇒ Мощность всего 29% !
Compare2/ Numerical observations/ Normal distributin/mean value
Тогда по тесту Стьюдента различия незначимы и Р = 0.159
Проверим мощность данного теста
Compare2/ Power/ Comparison of means
Size A - 100 Size B – 100
DETECT a difference 2
Чтобы выйти на мощность 80% объемы выборок должны быть 400 и 400
Compare2/ Sample size/ Means
Допустим, что для 2 выборок имеем:
О чем мы обязаны сообщить в публикации (правда биологи этого почти никогда не делают)
т.е. доля упущенных открытий более 70% !
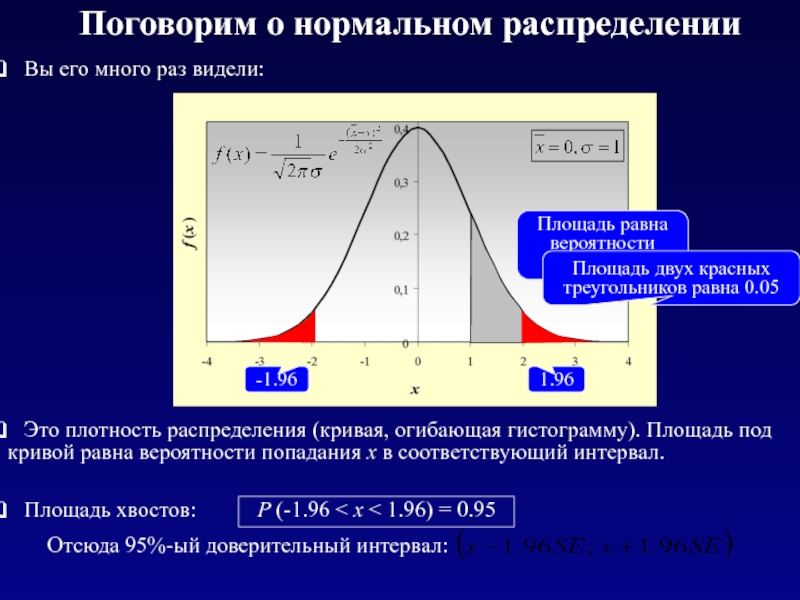
Слайд 28Поговорим о нормальном распределении
Это плотность распределения (кривая, огибающая гистограмму).
Площадь двух красных треугольников равна 0.05
Вы его много раз видели:
Слайд 29Почему нормальное распределение встречается на каждом шагу?
Например, биномиальный закон –
Нормальное распределение имеет любая величина, которая определяется суммой большого числа случайных слагаемых (ЦПТ).
Чем больше слагаемых – тем «нормальней»!
Проверяем ... К 20 годам 80% молодых людей курит. Какова вероятность, что среди 100 окажется 15 некурящих?
Среднее число некурящих Np =100⋅0.2=20,
дисперсия равна Np(1-p) = 100⋅0.2(1-0.2) = 16, σ = 4.
Р(15) = 0.048
Р(15) = 0.046
или
Слайд 30Пока мы говорили о сравнениях количественных признаков
Мы припомнили, что
Познакомились с дисперсионным анализом – методом одновременного сравнения нескольких выборок
Узнали, как обрабатывать данные, распределение которых существенно «ненормально»
Поговорили о том, как следует осмысливать и преподносить незначимые результаты
При этом:
Слайд 31Качественные признаки
Будет правильно, если вы скажите – мы этим уже
Но то было сравнение 2 частот. А как сравнивать несколько пар частот?
Например, распределения генотипов при различных вариантах скрещиваний – наблюдаемые и ожидаемые исходя из законов Менделя?
Или как сравнить в целом видовой состав в двух регионах? Или частоты встречаемости блондинов, брюнетов, шатенов и т.д. для 2 этносов
Во всех этих случаях речь идет либо о сравнении двух выборочных дискретных распределений, либо о сравнении наблюдаемого распределения с теоретически ожидаемым
Для решении этих задач разработаны тесты, называемые критериями согласия
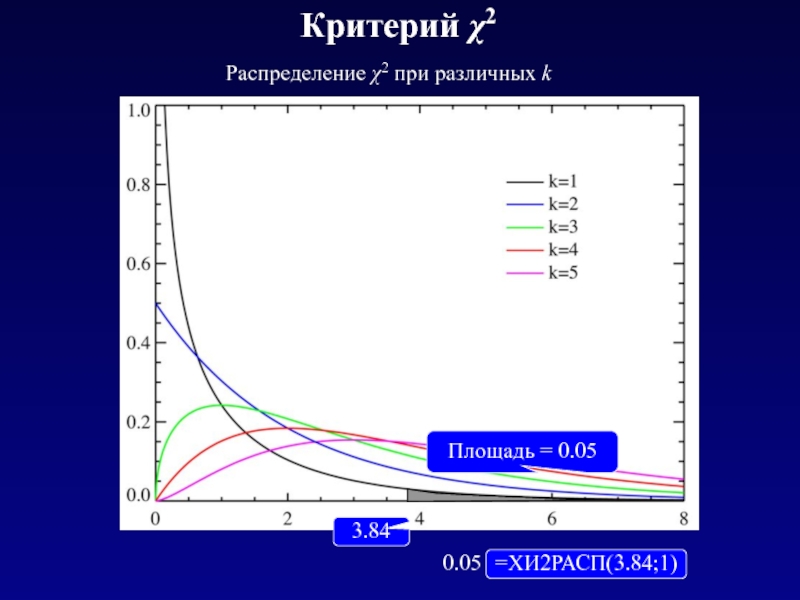
Слайд 32Критерий χ2
Вычисляется сумма
В 1900 г. Карл (Charles) Пирсон вычислил распределение
где все ξi - нормальны
k -1– число степеней свободы
Оказалось, что χ2 распределен как сумма квадратов независимых случайных величин:
т.е.
Если величина χ2 достаточно велика, то гипотеза о совпадении наблюдаемых и ожидаемых численностях отвергается.
Насколько велика скажет Excel:
=ХИ2РАСП(3.84;1)
0.05
Соответствие наблюдаемых численностей ожидаемым частотам
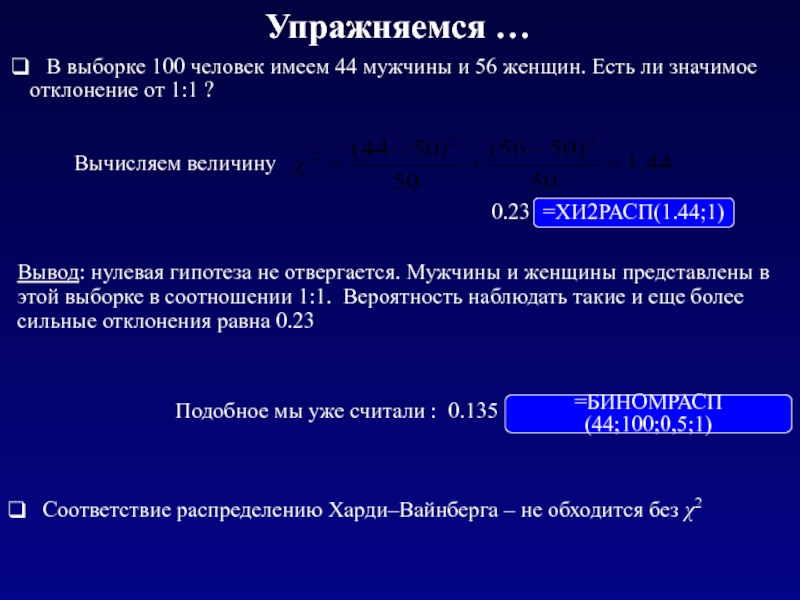
Слайд 34Упражняемся …
В выборке 100 человек имеем 44 мужчины
Вывод: нулевая гипотеза не отвергается. Мужчины и женщины представлены в этой выборке в соотношении 1:1. Вероятность наблюдать такие и еще более сильные отклонения равна 0.23
=ХИ2РАСП(1.44;1)
0.23
Подобное мы уже считали : 0.135
=БИНОМРАСП(44;100;0,5;1)
Соответствие распределению Харди–Вайнберга – не обходится без χ2
Слайд 35Соответствие распределению
Харди - Вайнберга
Как правило для популяционных частот генотипов АА,
соблюдается соотношение Харди–Вайнберга (а также Кастла и многих других). Закон настолько прост, что его открывали для себя многие, но стеснялись публиковать.
Т.е. не бывает: [100, 100, 100] , а лишь, например, [50, 100, 50]
и то же самое для численностей:
Я запишу это соотношение в виде:
Слайд 37Вывод: нулевая гипотеза не отвергается. Частоты генотипов соответствует распределению Харди-Вайнберга. Вероятность
0.727
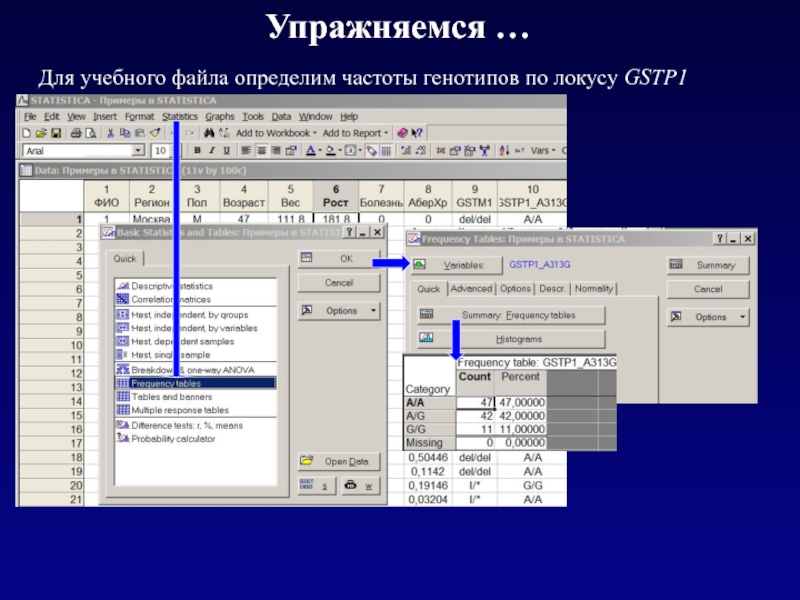
Для учебного файла определим частоты генотипов по локусу GSTP1
Упражняемся …
=ХИ2РАСП(0,122; 1)
Число степеней свободы 1, а не 2. Это потому, что мы вычисляли ожидаемые через наблюдаемые
Важное условие применимости χ2 :
все ожидаемые > 5
Слайд 38Что означают серьезные отклонения
от Харди – Вайнберга?
Основная причина
В принципе причинами отклонений от ХВ могут быть
- близкородственные скрещивания
- подразделенность популяции
- генетический дрейф
- отбор
Но самая реальная причина – ошибки генотипирования
Проверяйте ХВ, чтобы убедиться в том, что ваши праймеры
работают правильно
Слайд 39Критерий χ2 и таблицы сопряженности
Тест χ2 можно использовать для проверки
Вероятности независимых событий перемножаются.
Поэтому, если признак А не сопряжен (не связан) с признаком В, то таблица сопряженности этих признаков принимает вид:
_
_
_
Это и есть ожидаемые частоты
при условии, что признаки А и В никак не связаны
Признак А есть
Признака А нет
Теперь их можно сравнить с реально наблюдаемым распределением, используя χ2
Слайд 40Критерий χ2 и таблицы сопряженности
Как это делается практически?
_
_
_
_
5600
Делим на 200
_
_
Вычисляем:
=ХИ2РАСП(44,3; 1)
В общем случае:
(число столбцов-1)(число строк-1)
2,8⋅10-11
Наблюдаемые
Ожидаемые
А что скажет по этому поводу точный тест Фишера?
2,5⋅10-9
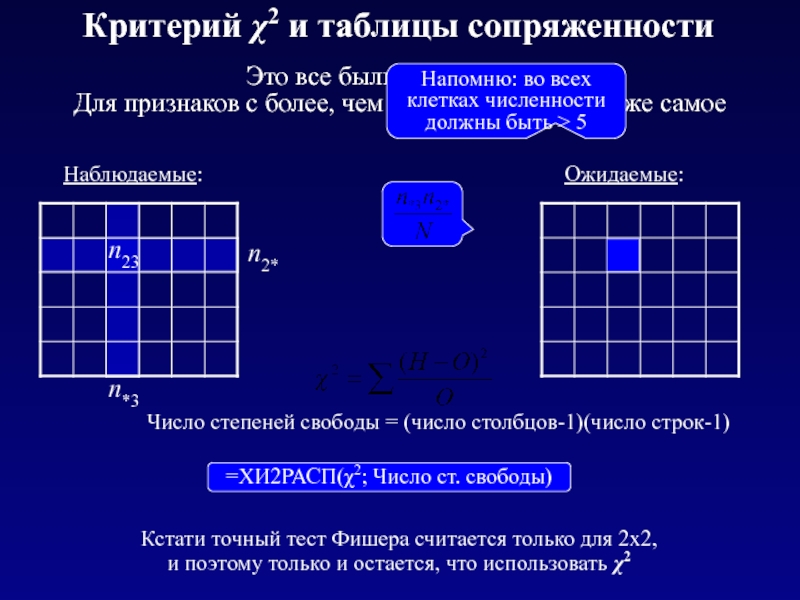
Слайд 42Критерий χ2 и таблицы сопряженности
Это все были таблицы 2х2.
Для
n23
Наблюдаемые:
Ожидаемые:
Число степеней свободы = (число столбцов-1)(число строк-1)
Кстати точный тест Фишера считается только для 2х2,
и поэтому только и остается, что использовать χ2
Напомню: во всех клетках численности должны быть > 5
=ХИ2РАСП(χ2; Число ст. свободы)
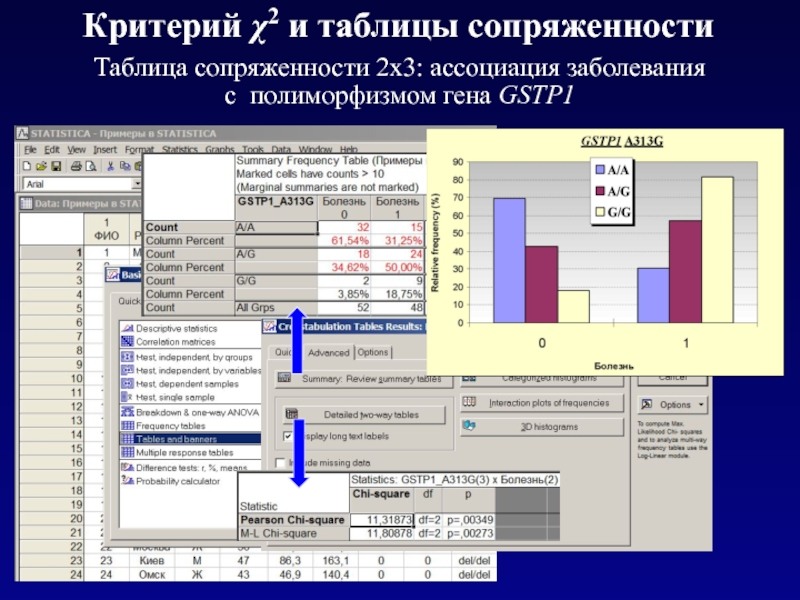
Слайд 43Критерий χ2 и таблицы сопряженности
Таблица сопряженности 2х3: ассоциация заболевания
с
Слайд 44Критерий χ2: проверка однородности данных
В практике экспериментатора постоянно возникает вопрос
Данные мониторинга популяций, полученные в различные годы
Сравнение частот аберраций для экспонированных и контрольных популяций: можно ли объединять данные для различных особей
Данные по частотам генов в нескольких выборках в пределах одно локальности
Объединие выборок возможно лишь при условии однородности данных. В случае таблиц сопряженности на однородность указывает низкий χ2 (соответствующее р > 0.1)
При работе с неоднородными данными возникают невероятные ситуации!
Слайд 45На сегодня это все
Напоследок хочу посоветовать:
При сравнении средних всегда
Проверяйте характер распределения сравниваемых величин. Или хотя бы стройте гистограммы распределений – для себя.
Оценивайте мощность теста в случае получения незначимых результатов
Прикиньте с помощью χ2 – соотношение мальчиков и девочек в вашей группе отличается значимо от 1:1 ?