- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторы. Скалярные величины презентация
Содержание
- 1. Векторы. Скалярные величины
- 2. СКАЛЯРНЫЕ ВЕЛИЧИНЫ Скалярная величина (скаляр) –
- 3. ВЕКТОРНЫЕ ВЕЛИЧИНЫ Векторная величина (вектор) – это
- 4. Вектором называется направленный
- 5. Векторы называются сонаправленными, если
- 6. Если векторы лежат на перпендикулярных прямых, то
- 7. РАВЕНСТВО ВЕКТОРОВ Векторы являются равными, если
- 8. СЛОЖЕНИЕ ВЕКТОРОВ ПО ПРАВИЛУ ТРЕУГОЛЬНИКА 1.Правилом треугольника
- 9. СЛОЖЕНИЕ ВЕКТОРОВ ПО ПРАВИЛУ ПАРАЛЛЕЛОГРАММА Сложение векторных
- 10. ВЫЧИТАНИЕ ВЕКТОРОВ Чтобы из вектора
- 11. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 1.Сложение по правилу треугольника 2.Сложение по правилу параллелограмма 3. Правило вычитания
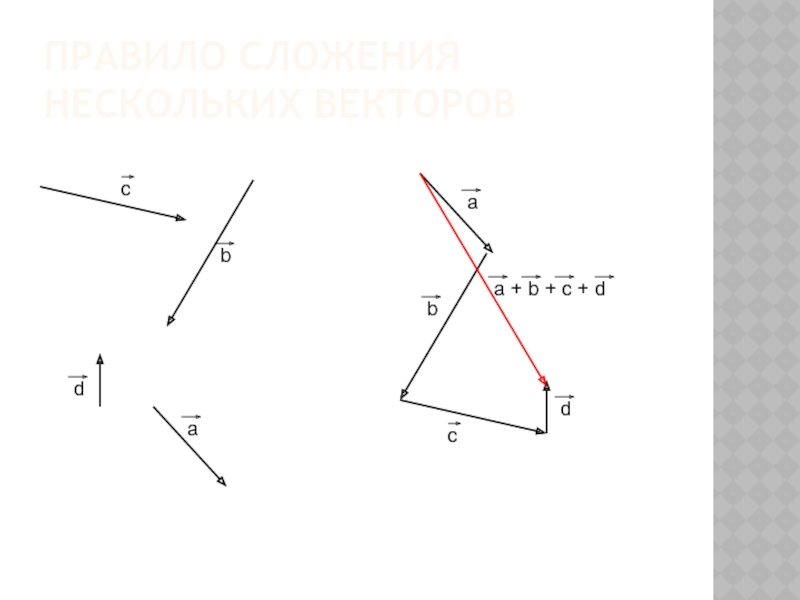
- 12. ПРАВИЛО СЛОЖЕНИЯ НЕСКОЛЬКИХ ВЕКТОРОВ
- 13. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО Произведением ненулевого вектора
- 14. КООРДИНАТЫ ВЕКТОРА А В Правила: Каждая
- 15. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. Скалярным произведением
- 16. ФОРМУЛЫ В КООРДИНАТАХ. • •
- 17. СЛЕДСТВИЯ Ненулевые векторы а{x1;y1} и
- 18. СПАСИБО ЗА ВНИМАНИЕ
Слайд 2СКАЛЯРНЫЕ ВЕЛИЧИНЫ
Скалярная величина (скаляр) – это физическая величина, которая имеет
Слайд 3ВЕКТОРНЫЕ ВЕЛИЧИНЫ
Векторная величина (вектор) – это физическая величина, которая имеет две
Примеры векторных величин: скорость (), сила (), ускорение () и т.д.
Слайд 4
Вектором называется направленный отрезок.
Модулем вектора называется длина содержащего
l AB l=AB
Ненулевые векторы называются коллинеарными, если они лежат
либо на одной, либо на параллельных прямых.
Слайд 5
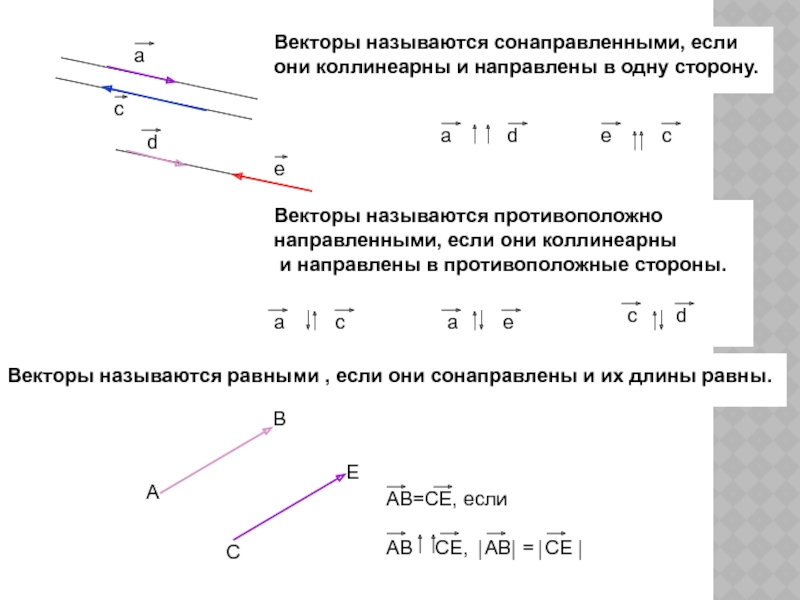
Векторы называются сонаправленными, если
они коллинеарны и направлены в одну сторону.
Векторы называются
направленными, если они коллинеарны
и направлены в противоположные стороны.
Векторы называются равными , если они сонаправлены и их длины равны.
А
В
С
Е
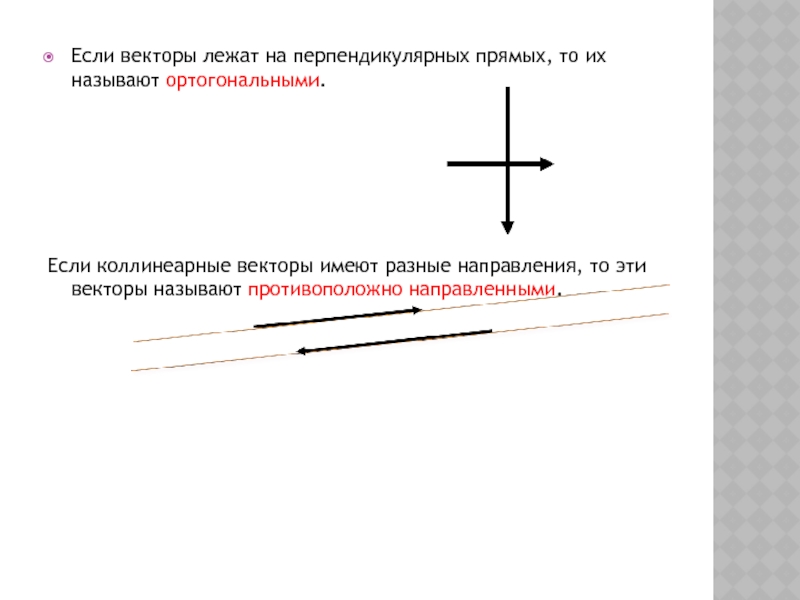
Слайд 6Если векторы лежат на перпендикулярных прямых, то их называют ортогональными.
Если коллинеарные
Слайд 7РАВЕНСТВО ВЕКТОРОВ
Векторы являются равными, если они сонаправлены и их модули
? ⃗ ↑↑? ⃑ и |? ⃗ | = |? ⃗ |, то ? ⃗ = ? ⃗
Слайд 8СЛОЖЕНИЕ ВЕКТОРОВ ПО ПРАВИЛУ ТРЕУГОЛЬНИКА
1.Правилом треугольника сложения векторов называется следующий способ:
Пусть есть произвольные векторы и . Надо от конца вектора отложить вектор , равный вектору . Тогда вектор, начало которого совпадает с началом вектора
, а конец совпадет с концом вектора , будет суммой .
Слайд 9СЛОЖЕНИЕ ВЕКТОРОВ ПО ПРАВИЛУ ПАРАЛЛЕЛОГРАММА
Сложение векторных величин производится по правилу параллелограмма:
Слайд 10ВЫЧИТАНИЕ ВЕКТОРОВ
Чтобы из вектора вычесть вектор надо к вектору
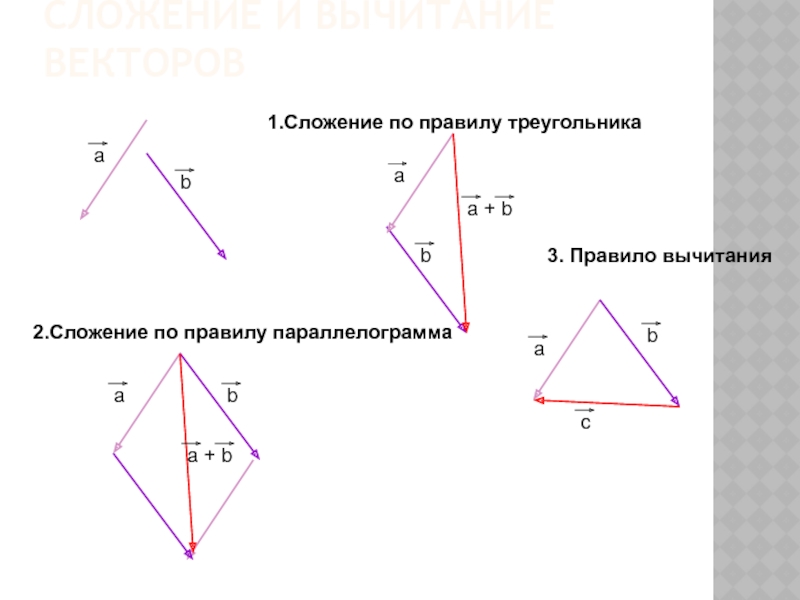
Слайд 11СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
1.Сложение по правилу треугольника
2.Сложение по правилу параллелограмма
3. Правило
Слайд 13УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО
Произведением ненулевого вектора
на число k называется
Длина которого равна l k l·l l , причем векторы
и cонаправлены при k≥0 и
противоположно направлены при k≤0.
Слайд 14
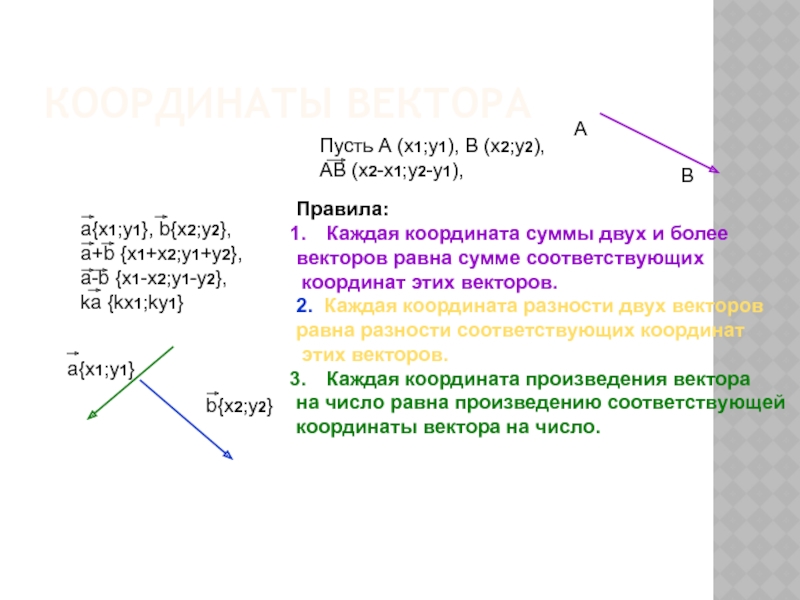
КООРДИНАТЫ ВЕКТОРА
А
В
Правила:
Каждая координата суммы двух и более
векторов равна сумме соответствующих
2. Каждая координата разности двух векторов
равна разности соответствующих координат
этих векторов.
Каждая координата произведения вектора
на число равна произведению соответствующей
координаты вектора на число.
Слайд 15
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ.
Скалярным произведением двух векторов называется произведение
их длин на
Слайд 16
ФОРМУЛЫ В КООРДИНАТАХ.
•
•
2.Расстояние между двумя точками
А(х1;у1)
В(х2;у2)
3.Вычисление длины вектора
Слайд 17
СЛЕДСТВИЯ
Ненулевые векторы а{x1;y1} и b{x2;y2} перпендикулярны
тогда и только тогда, когда
т.е. х1х2+у1у2=0.