Задачи с параметрами презентация

теме, задачей которого является научить методам решения таких задач на основе часто встречаемых типов. Курс рассчитан на последовательное изучение его, начиная с 8 класса, так в I полугодие учащимся 8 классов можно предложить изучение:
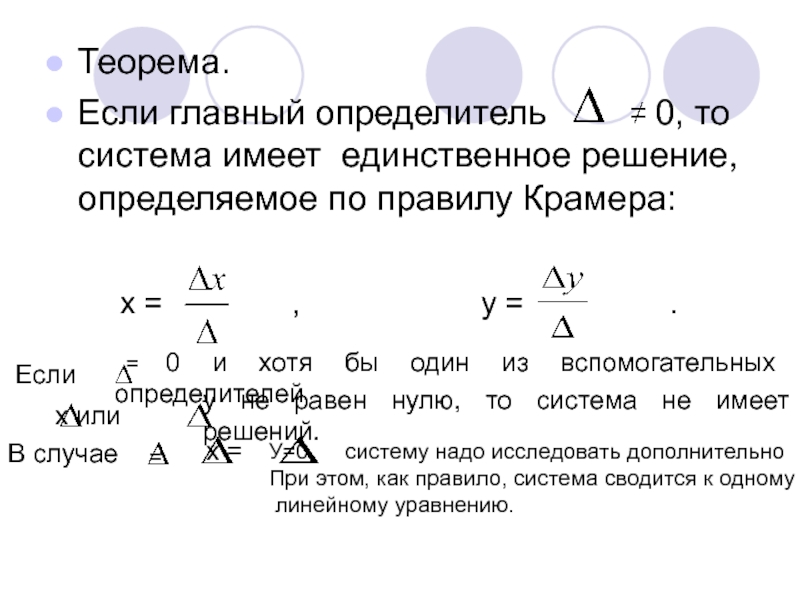
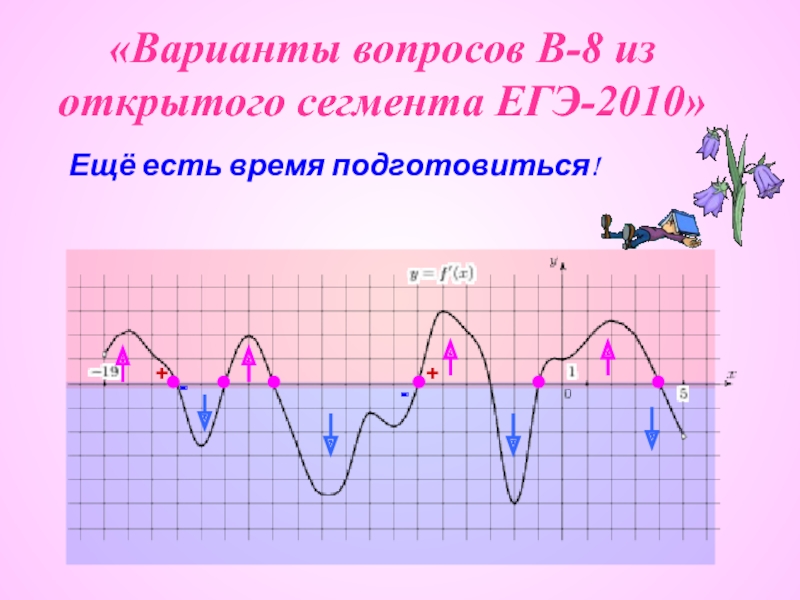
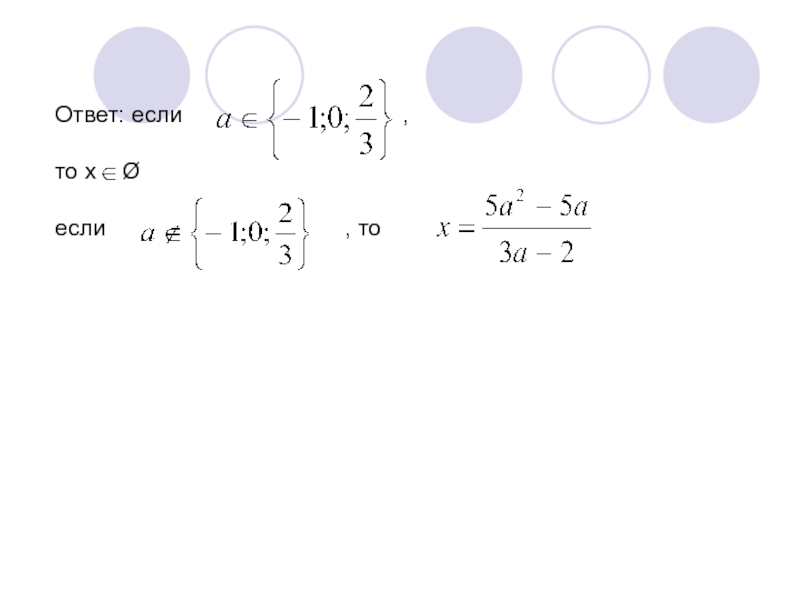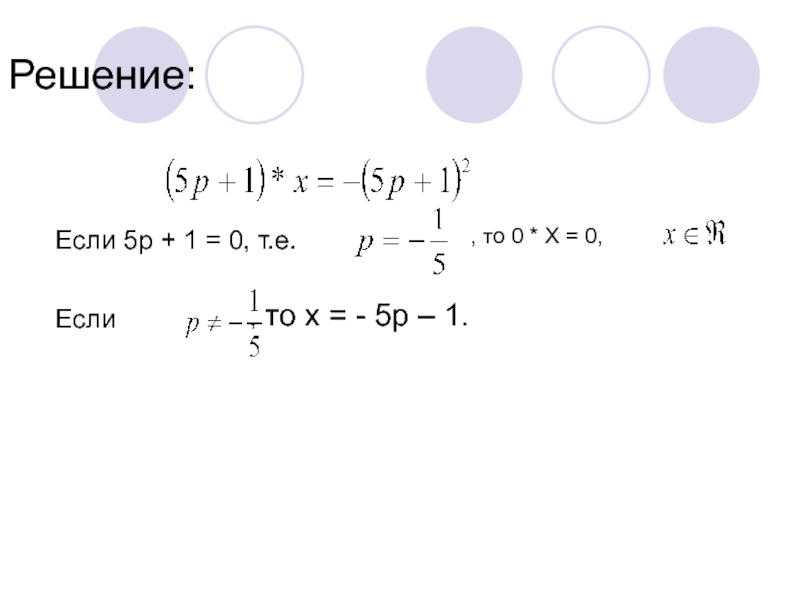- Линейные уравнения, системы уравнений, неравенства, содержащие параметры.
В 9 классе :
- Квадратные уравнения и неравенства. Системы уравнений и неравенств второго порядка.
В 10 классе:
- Иррациональные уравнения и неравенства;
- Показательные и логарифмические уравнения и неравенства;
- Тригонометрические уравнения и неравенства.
В 11 классе:
- Применение производной;
- Графический метод решения и метод решения относительно параметра;

900igr.net

Количество часов
§ 1. Линейные уравнения, 5ч
§ 2. Системы линейных уравнений 5 ч
Задачи, предлагаемые на экзаменах
§ 3. Линейные неравенства 5 ч.
Зачет 2 ч.
Итого: 17 ч.

В,
где А, В - выражения, зависящие от параметров,
Х - неизвестное, называется линейным уравнением с
параметрами.

Схема исследования:
Если А=0, В0, то имеем 0 * Х = В, уравнение не имеет решений.
Если А=0, В=0, то 0 * Х = 0, уравнение имеет решением множество всех действительных чисел.
Если А0, В - любое, то уравнение имеет единственное решение .

Замечание:
Если линейное уравнение не представлено в виде (1), то сначала нужно привести его к стандартному виду (1) и только после этого проводить исследование.

записано в стандартном виде.
Если К+4=0, т.е. К=-4, то уравнение имеет вид
0 * Х = -7, т.е. не имеет решений: Ø.
Если К+4 0, т.е. К -4, то уравнение имеет

единственное решение

Ответ: если К=-4, то Ø, если К -4, то

уравнение в стандартном виде


1. Если , т.е. , то имеем 0 * Х = 0, решением является множество действительных чисел:
2. Если , то
Ответ: Если , то ,

Если , то х=-4.

, т.е. при р=1 уравнение имеет вид 0 * Х = 2, следовательно,
х Ø, при р=-1, уравнение имеет вид
0 * Х = 0, следовательно, х .
если , то
Ответ: если р=1, х Ø; если р=-1, х ; если , .

уравнение не имеет смысла, поэтому оно при а = -1 не имеет решения: х Ø.
При а -1, то уравнение равносильно системе:

вид
0 * Х = , х Ø.

если то теперь найдем те

значения параметра а, при которых х = 2а, т.е. система не имеет решения.

Имеем:

Следовательно, при а = 0 или а = - 1 исходное уравнение также как и при не имеет решения.

, то х Ø если , то

если а=2, то 0 * Х = -7, х Ø

если , то .

, то исходное

уравнение также не имеет решения.
Ответ: , то х Ø;

, то .

лучу .

Решение:
1.
.
Если а = 1, то 0 * Х = - 4, х Ø

Если а = - 1, то 0 * Х = 0,
Условия задачи не выполняются

по условию задачи х

Откуда

из найденного множества значений а надо исключить
а = -1,

Ответ:

имеет не менее двух различных решений.

Решение:
Если линейное уравнение имеет 2 и более решений, то оно имеет бесконечное множество решений.
Значит, .


Ответ: при , .

имеет решений.

Решение:




Ответ: при , (или
, ) .

Х = 0,

Если

, то х = - 5р – 1.

- 1) = а – 1.
Если а – 1 =0, т.е. а = 1, 0 * Х = 0,

Если

, то х = 1.
Ответ: Если а – 1 =0, то

Если

, то х = 1.

Х = 4, х Ø
если р = - 2, то 0 * Х = 0, если , то ,

если

, то

Ответ: если р = 2, х

Ø; если р = - 2,

если

,

.

= 0,

если р = - 1, то 0 * Х = 4, х

Ø

Ответ: если р = 1,

если р = - 1, х

Ø;

,

.

3 – 2р, причем, если – 3 – 2р = 0, т.е.

, то 0 * Х = 0,

или

, то 0 * Х = - 3 – 2р х

Ø.

если

2 .если

, то

Ответ: если

,

,

если

,

, х

Ø; если

,

,

Где , , , , , - выражения, зависящие от параметров, х, у – неизвестные, называется системой двух линейных алгебраических уравнений с двумя неизвестными в параметрах.

системы зависят от нескольких параметров, то исследовать систему удобно с помощью определителей системы:
= = - ,

х = = - ,

У = = - .

имеет единственное решение, определяемое по правилу Крамера:

х = , у = .

Если

= 0 и хотя бы один из вспомогательных определителей

х или

у не равен нулю, то система не имеет решений.

В случае

=

х =

У=0 систему надо исследовать дополнительно
При этом, как правило, система сводится к одному
линейному уравнению.

систему следующим образом:
Решая уравнение = 0, найдем конкретные значения параметров или выразим один из параметров через остальные и подставим эти значения параметров в систему. Тогда получим систему с конкретными числовыми коэффициентами или с меньшим числом параметров, которую и надо исследовать.

х = 1 – ау, и подставим в первое уравнение: а (1 – ау) – 3ау = 2а + 3 - а (а + 3) у = а + 3.

Возможны случаи:
1) а = 0. тогда уравнение имеет вид 0 * у = 3

у

Ø.
Следовательно, при а = 0 система не имеет решений.

2) а = - 3. Тогда 0 * у = 0

у

При этом х = 1 – ау = 1 + 3у.
3) а

0, а

- 3. Тогда

=2.

х = 1 – ау = 1 – а

Ответ:
Если а = 0, то (х;у)

Если а = - 3, то х = 1 + 3у, у

;
Если а

0, а

- 3, то х = 2, у =

.

Ø

=

= (а+5) (5а+6) - (2а+3) (3а+10) = а (2-а),

х =

= (3а+2) (5а+6) - (2а+3) (2а+4) = а (11а+14),

у =

= (а+5) (2а+4) - (3а+2) (3а+10) = - а (7а+22).

- 2, тогда

=

=

,

2) = а (2-а) = 0 а = 0 или а = 2.

у =

= -

=

.

При а = 0, определители х = у = 0.
Тогда система имеет вид:

5х + 3у = 2

х

,

у =

.

утверждать, что система не имеет решений.

Ответ: если а 0 и а 2, то х = ,
у = ;

Если а = 0, то х , у = ;

Если а = 2, то (х;у) Ø. ;

Ax B, где
А, В - выражения, зависящие от параметров
а х - неизвестное, называется линейными неравенствами с параметрами

множество решений заданного неравенства.

Неравенство вида Ах > B, решается по схеме:
1) если А > 0, то х > В/А.
2) если А < 0, то х < В/А.
3) если А = 0, то неравенство имеет вид 0 * х > В. При В 0 неравенство имеет пустое множество решений; при В < 0 решением неравенства будет множество всех действительных чисел .

> - 1

Решение:
1) р - 1 > 0 р > 1, тогда х >
х > р + 1;
2) р - 1 < 0 р < 1, тогда х <
х < р + 1;
3) р - 1 = 0 р = 1, неравенство имеет вид 0*х > 0, х Ø.
Ответ: если р > 1, то х > р + 1; если р < 1, то х < р + 1; если р = 1, то х Ø.

системы сведем к исследованию линейного уравнения.
Умножив второе уравнение системы на (- 5), первое на (3) и сложим уравнения:
12у – 10ау = 3 – 5в, у (12 – 10а) = 3 – 5в (1).
Уравнение (1) не имеет решения, если
12 – 10а = 0 и 3 – 5в 0, т.е. а = , в .
Ответ: а = , в .

и 4х + 3у = 3 пересекаются?

Прямые пересекаются, если система уравнений

имеет единственное решение.
Первое уравнение умножаем на (- 2) и сложим со вторым:
- 2ау + 3у = 4 + 3, у( - 2а + 3) = 7.
Если – 2а + 3 0, т.е. а , то система
имеет единственное решение.
Ответ: а .

имеет решений.

Решение:
Первое уравнение умножим на 3 и сложим со вторым:
3ах + 6х = - 3 + в + 3, т.е. х (3а + 6) = в (2).
Если 0*х = в, то уравнение (2) не имеет решений, а следовательно, и исходная система уравнений.
Значит а = - 2, в 0.
Ответ: а = - 2, в 0.

изучивший школьную программу, сможет перенести методы решения уравнений и неравенств на уравнения и неравенства с параметрами. Трудности решения такого рода задач вызваны прежде всего тем, что даже при решении простейших уравнений и неравенств, содержащих параметры, приходится производить ветвление всех значений параметра на отдельные классы, при каждом из которых задача имеет решение.
Автор подробно рассматривает методы решения линейных уравнений и сводящихся к ним уравнений с одним и двумя параметрами, анализирует подходы к задачам на решение уравнений при всех значениях параметров и на поиск таких значений, при которых решения уравнений существуют и удовлетворяют некоторым дополнительным условиям.
Рассматриваются системы уравнений с двумя неизвестными, исследовать которые удобнее всего с помощью правила Крамера. Отдельно выделены задачи, предлагаемые ЦТ по математике.
Линейные неравенства с параметрами требуют исключительной точности выполнения преобразований.
В элективном курсе разобрано очень большое количество задач. Особое внимание уделяется отработке навыков равносильных преобразований и перебора всех возможных вариантов без исключения.
канд. Физ.-мат. наук, доцент кафедры
естественнонаучных дисциплин ГОУ «ЧРИО» Ярдухин А.К.