- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Углы, связанные с окружностью презентация
Содержание
- 1. Углы, связанные с окружностью
- 2. Углы, связанные с окружностью
- 3. Вписанный угол Вписанный угол равен половине
- 4. Угол между касательной и хордой
- 5. Угол с вершиной внутри окружности
- 6. Угол с вершиной вне окружности
- 7. Угол с вершиной вне окружности
- 8. Угол с вершиной вне окружности
- 9. Упражнение 1 Чему равен
- 10. Упражнение 2 Найдите центральный
- 11. Упражнение 3 Угол ACB
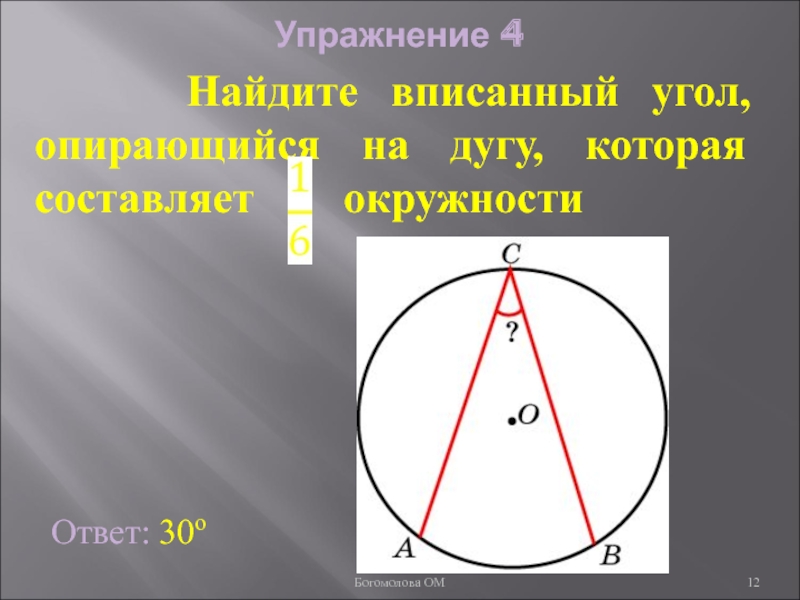
- 12. Упражнение 4 Ответ: 30о
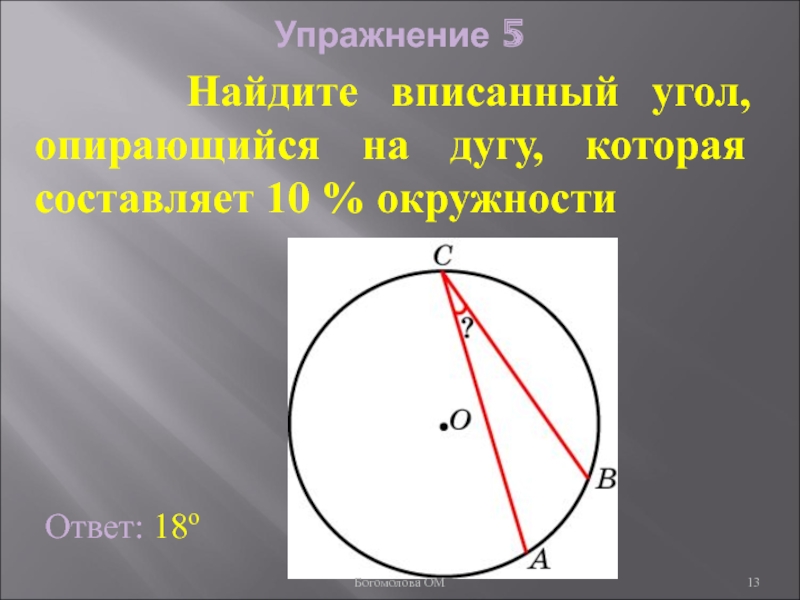
- 13. Упражнение 5 Ответ: 18о
- 14. Упражнение 6 Вписанный угол
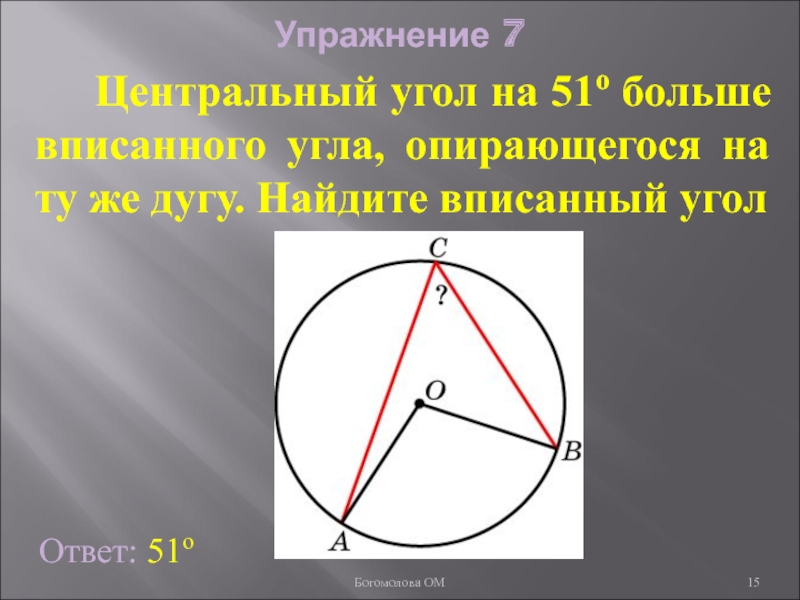
- 15. Упражнение 7 Центральный угол
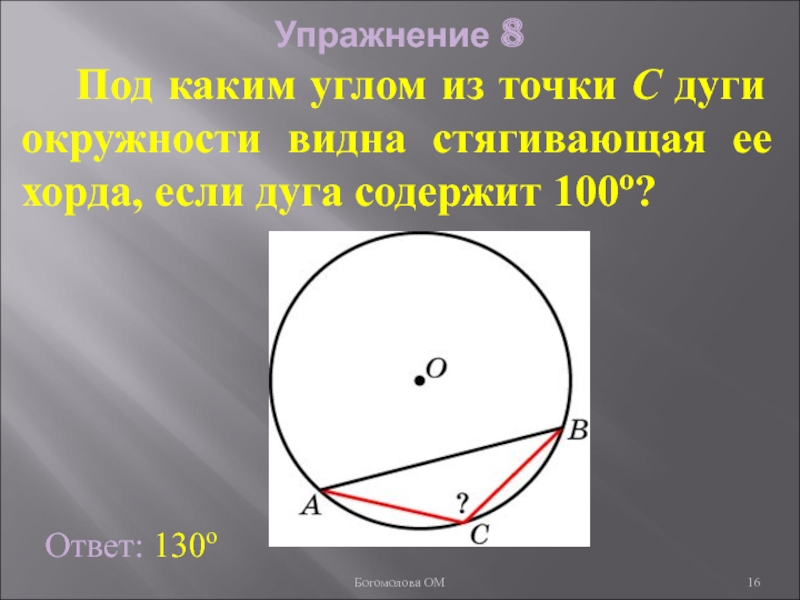
- 16. Упражнение 8 Под каким углом
- 17. Упражнение 9 Под каким
- 18. Упражнение 10 Угол ACB,
- 19. Упражнение 11 Ответ: 50о
- 20. Упражнение 12 Ответ: 45о
- 21. Упражнение 13 Ответ: 30о
- 22. Упражнение 14 На рисунке угол ACB равен
- 23. Упражнение 15 Углы ABC
- 24. Упражнение 16 Хорда CD
- 25. Упражнение 17 На рисунке
- 26. Упражнение 18 Стороны угла
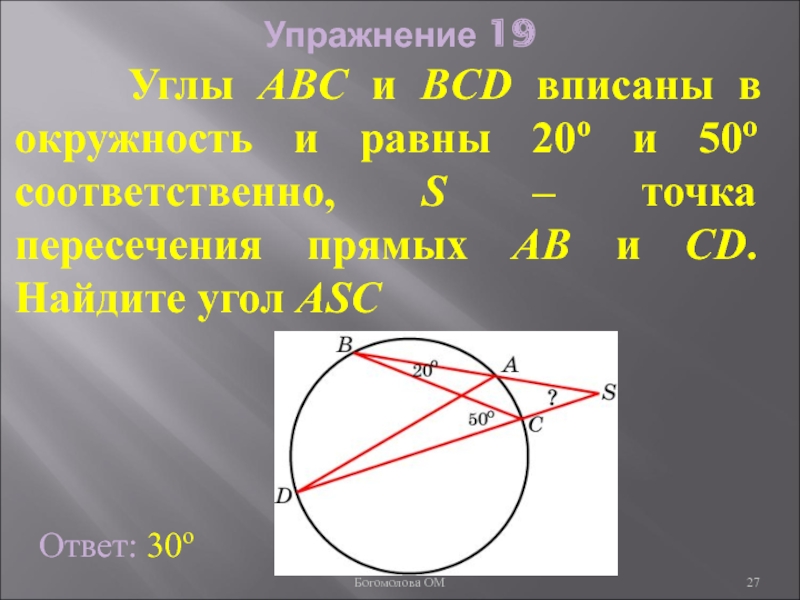
- 27. Упражнение 19 Углы ABC
- 28. Упражнение 20 Стороны угла
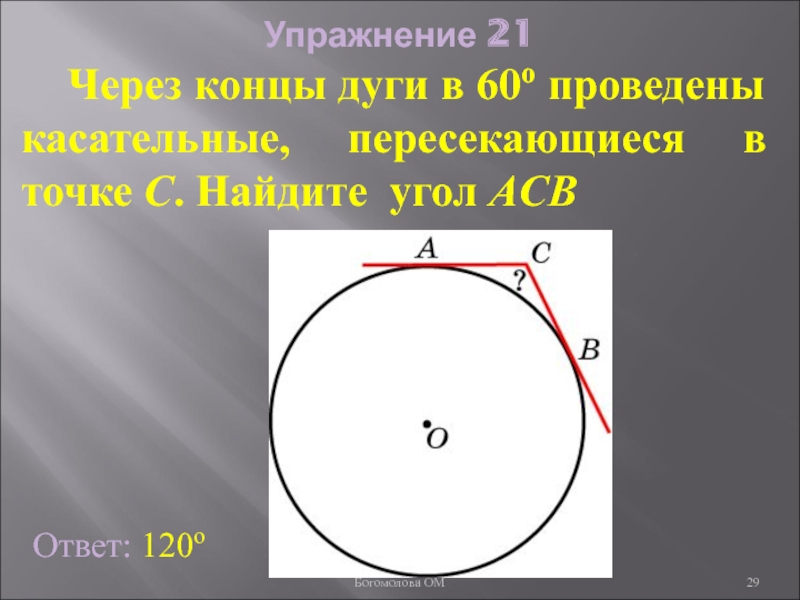
- 29. Упражнение 21 Через концы дуги
- 30. Упражнение 22 Хорда АВ
- 31. Упражнение 23 Две равные
- 32. Упражнение 24 Острый вписанный
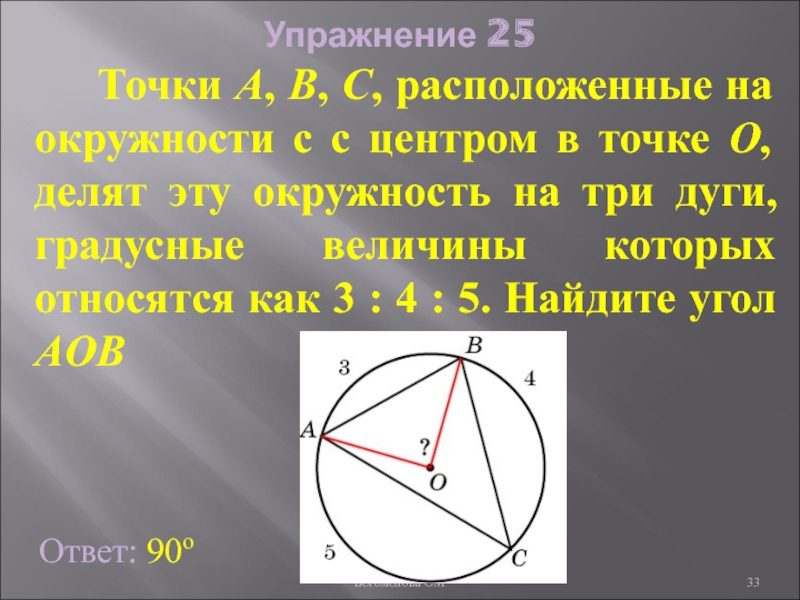
- 33. Упражнение 25 Ответ: 90о
- 34. Упражнение 26 Ответ: 105о
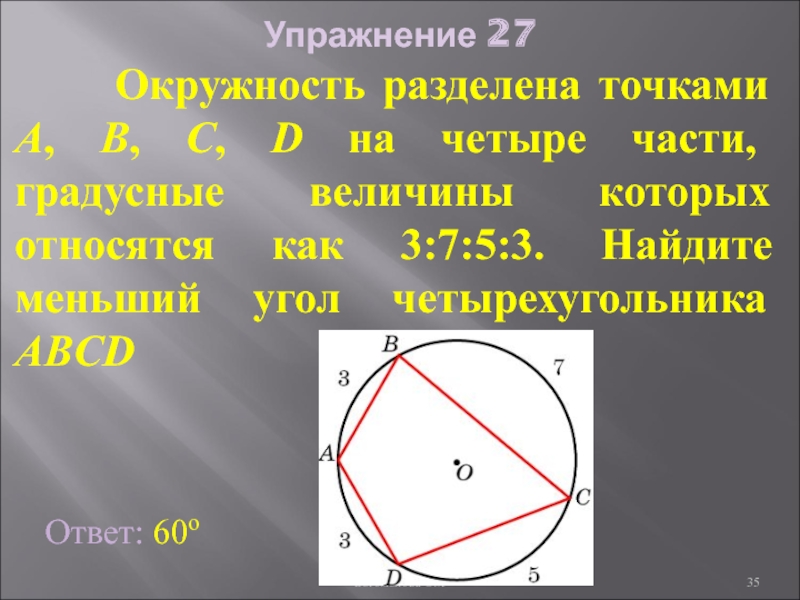
- 35. Упражнение 27 Окружность разделена
- 36. Упражнение 28 В четырехугольнике
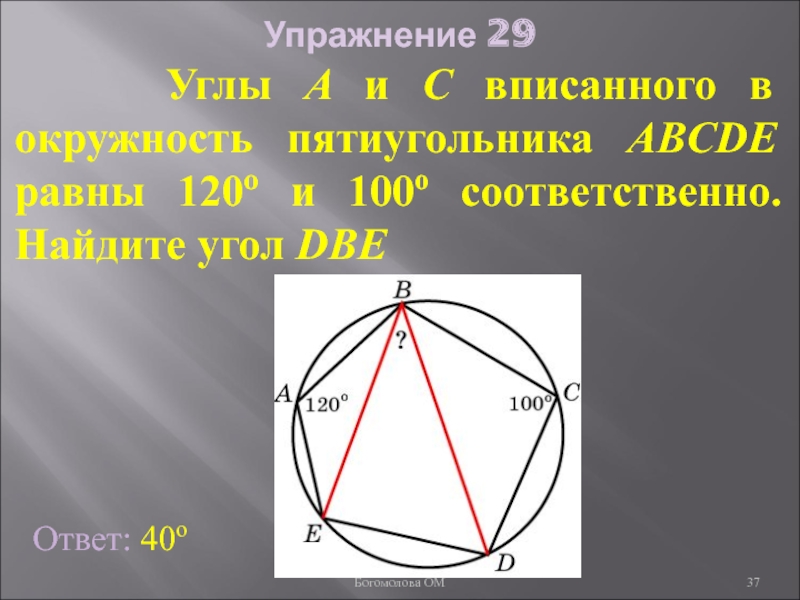
- 37. Упражнение 29 Углы A
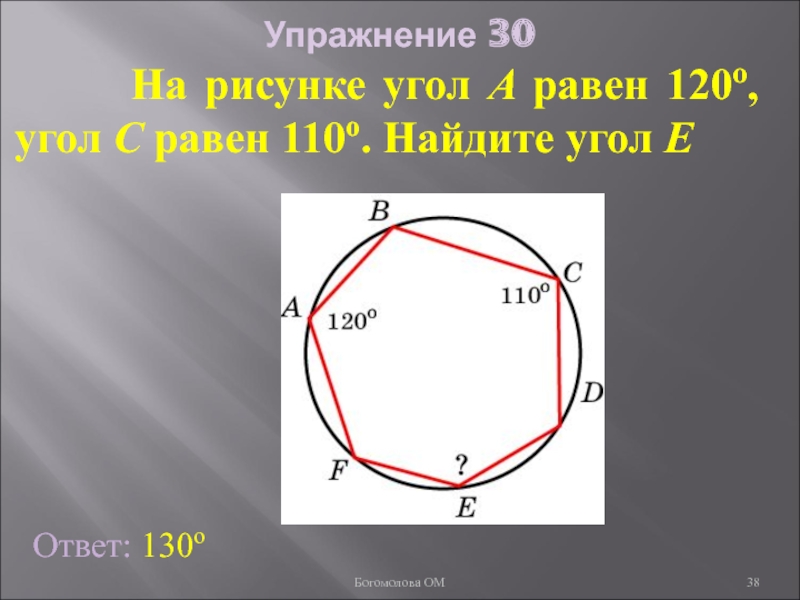
- 38. Упражнение 30 На
- 39. Упражнение 31 Хорда CD перпендикулярна
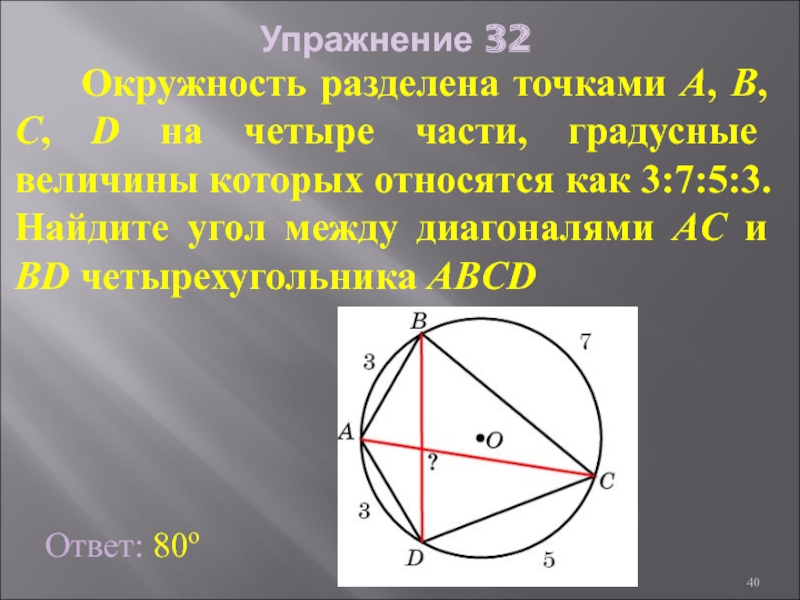
- 40. Упражнение 32 Окружность разделена
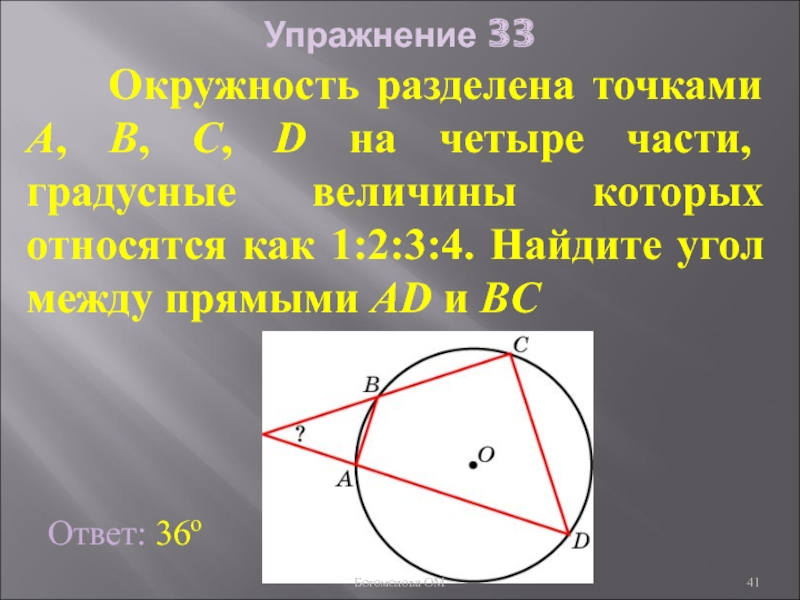
- 41. Упражнение 33 Окружность разделена
- 42. Упражнение 34 Из точки
- 43. Упражнение 35 В угол
- 44. Упражнение 36 В угол АСB,
- 45. Упражнение 37 В угол
- 46. Упражнение 38 Окружность разделена точками
- 47. Упражнение 39 Треугольник ABC
- 48. Упражнение 40 Треугольник ABC
- 49. Упражнение 41 Стороны четырехугольника
- 50. Упражнение 42 Две окружности
Слайд 2Углы, связанные с окружностью
Угол с вершиной в центре
Угол, вершина которого принадлежит окружности, а стороны пересекают окружность, называется вписанным
Каждый центральный угол данной окружности определяют дугу окружности, которая состоит из точек окружности, принадлежащих этому углу
Богомолова ОМ
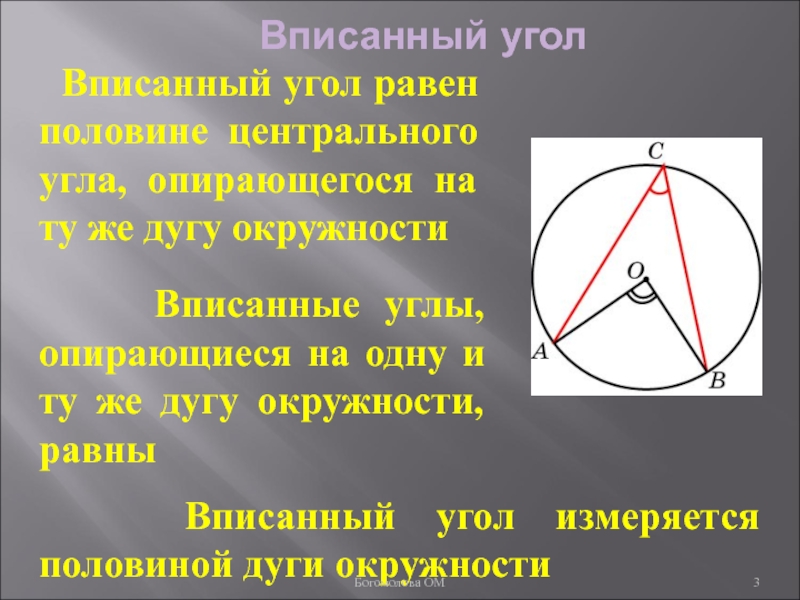
Слайд 3Вписанный угол
Вписанный угол равен половине центрального угла, опирающегося на ту
Вписанный угол измеряется половиной дуги окружности
Вписанные углы, опирающиеся на одну и ту же дугу окружности, равны
Богомолова ОМ
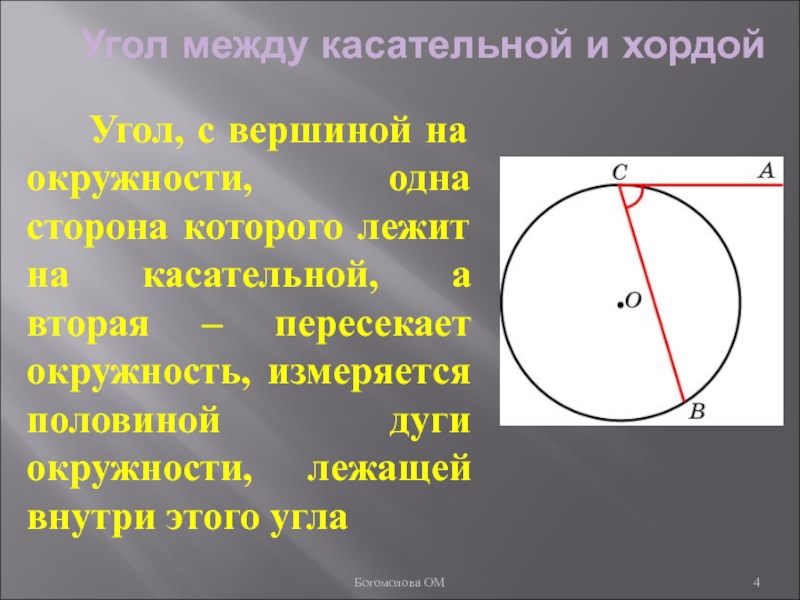
Слайд 4Угол между касательной и хордой
Угол, с вершиной на
Богомолова ОМ
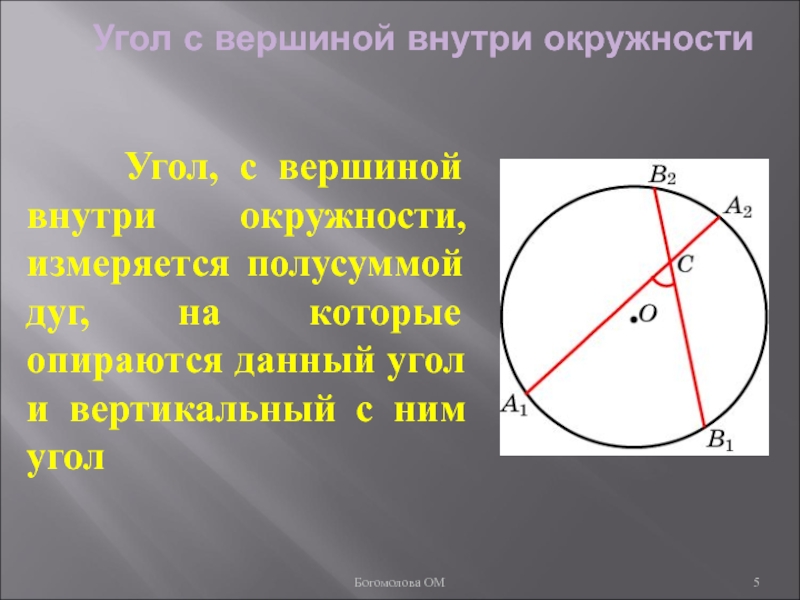
Слайд 5Угол с вершиной внутри окружности
Угол, с вершиной внутри
Богомолова ОМ
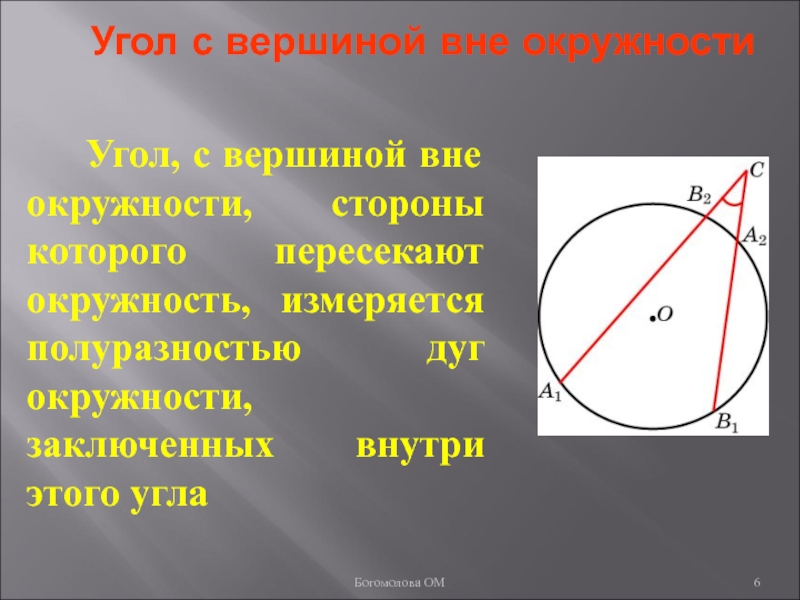
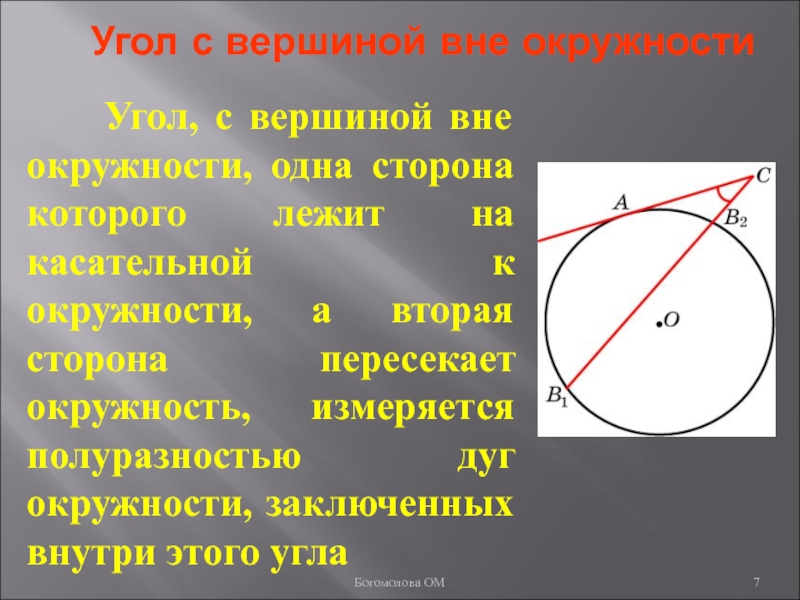
Слайд 6Угол с вершиной вне окружности
Угол, с вершиной вне
Богомолова ОМ
Слайд 7Угол с вершиной вне окружности
Угол, с вершиной вне
Богомолова ОМ
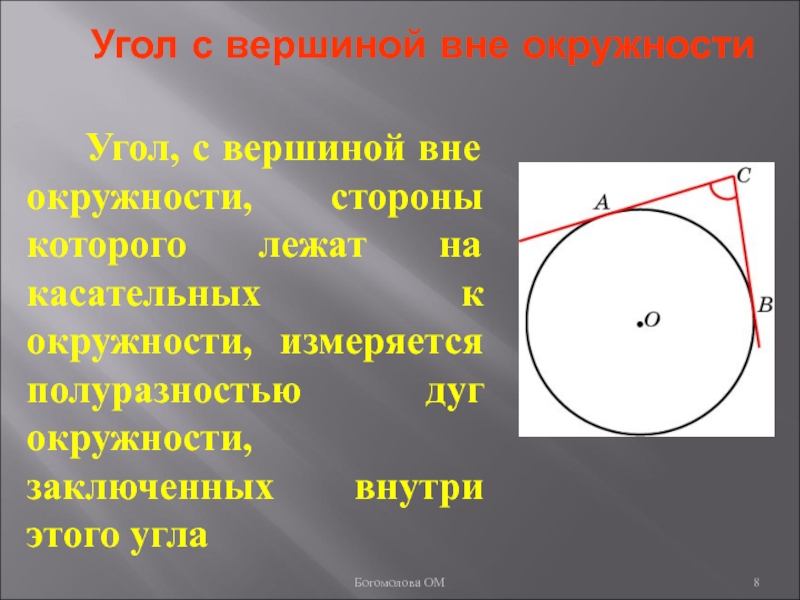
Слайд 8Угол с вершиной вне окружности
Угол, с вершиной вне
Богомолова ОМ
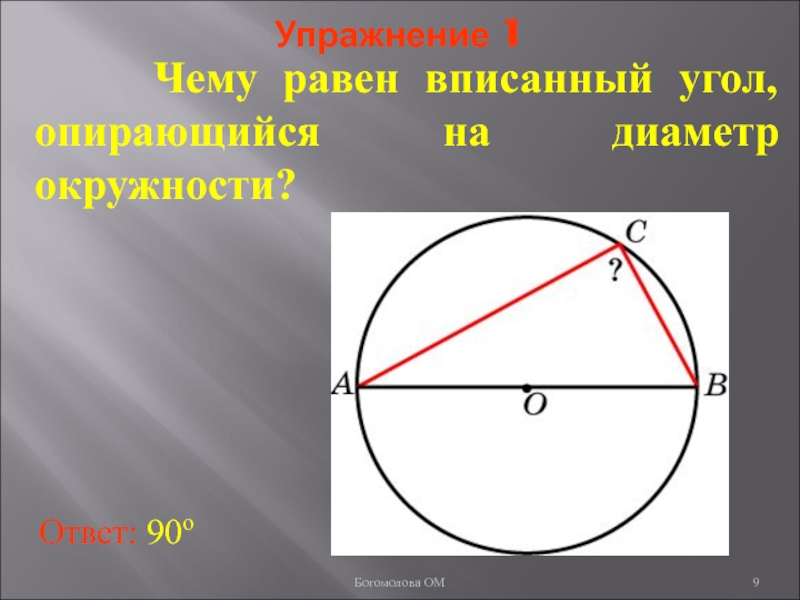
Слайд 9Упражнение 1
Чему равен вписанный угол, опирающийся на диаметр
Ответ: 90о
Богомолова ОМ
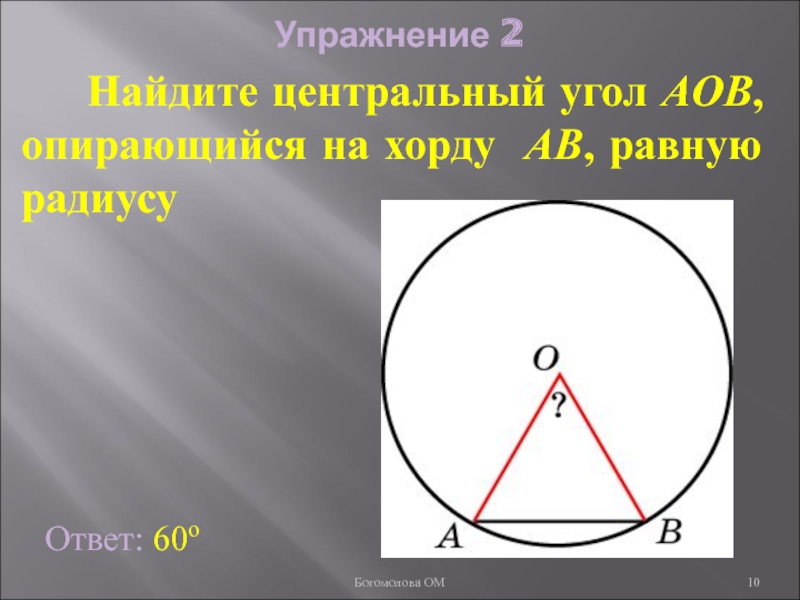
Слайд 10Упражнение 2
Найдите центральный угол AOB, опирающийся на хорду
Ответ: 60о
Богомолова ОМ
Слайд 11Упражнение 3
Угол ACB вписан в окружность. Градусные величины
Ответ: 107о
Богомолова ОМ
Слайд 12Упражнение 4
Ответ: 30о
Найдите вписанный угол, опирающийся на дугу,
Богомолова ОМ
Слайд 13Упражнение 5
Ответ: 18о
Найдите вписанный угол, опирающийся на дугу,
Богомолова ОМ
Слайд 14Упражнение 6
Вписанный угол на 35° меньше центрального угла,
Ответ: 35о
Богомолова ОМ
Слайд 15Упражнение 7
Центральный угол на 51о больше вписанного угла,
Ответ: 51о
Богомолова ОМ
Слайд 16Упражнение 8
Под каким углом из точки C дуги окружности
Ответ: 130о
Богомолова ОМ
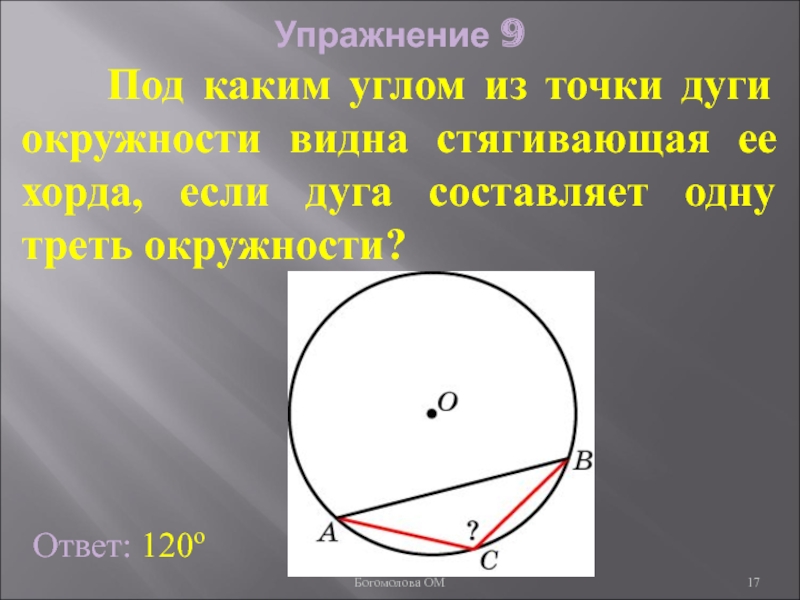
Слайд 17Упражнение 9
Под каким углом из точки дуги окружности
Ответ: 120о
Богомолова ОМ
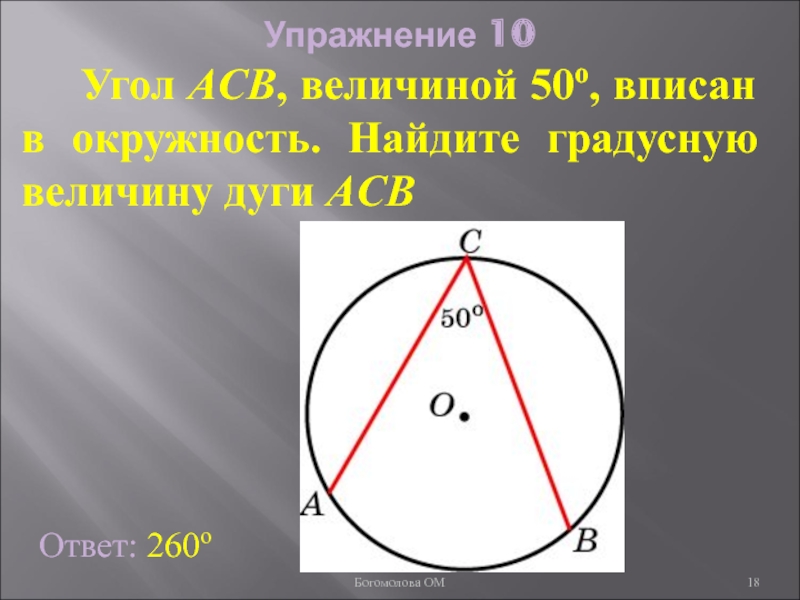
Слайд 18Упражнение 10
Угол ACB, величиной 50о, вписан в окружность.
Ответ: 260о
Богомолова ОМ
Слайд 19Упражнение 11
Ответ: 50о
Вершины треугольника ABC, вписанного в
Богомолова ОМ
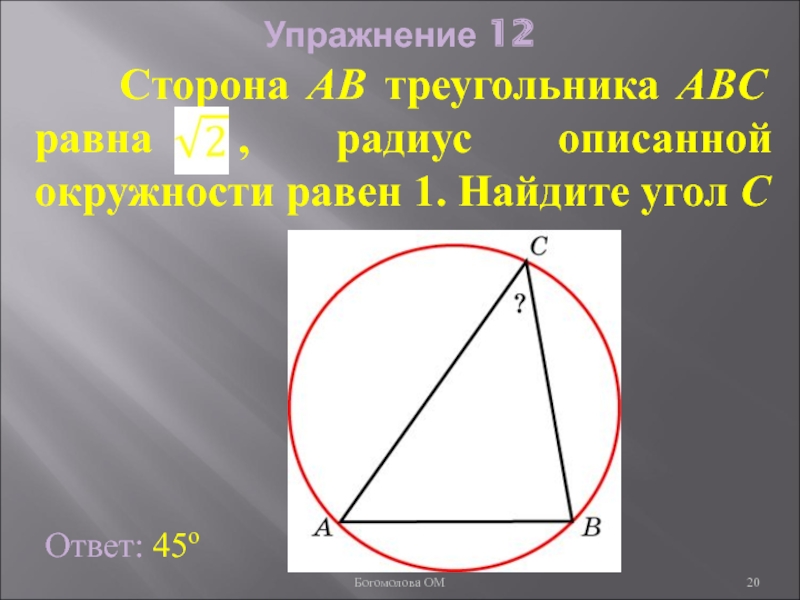
Слайд 20Упражнение 12
Ответ: 45о
Сторона AB треугольника ABC равна
Богомолова ОМ
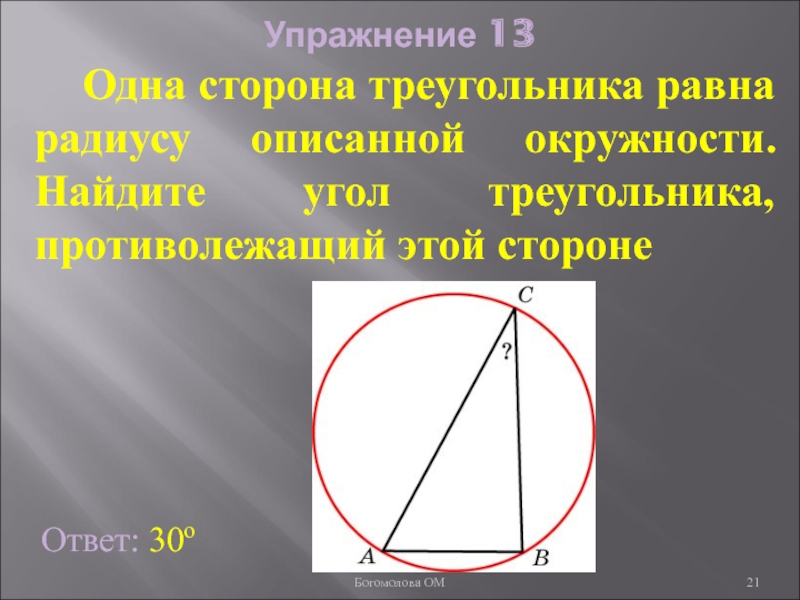
Слайд 21Упражнение 13
Ответ: 30о
Одна сторона треугольника равна радиусу описанной
Богомолова ОМ
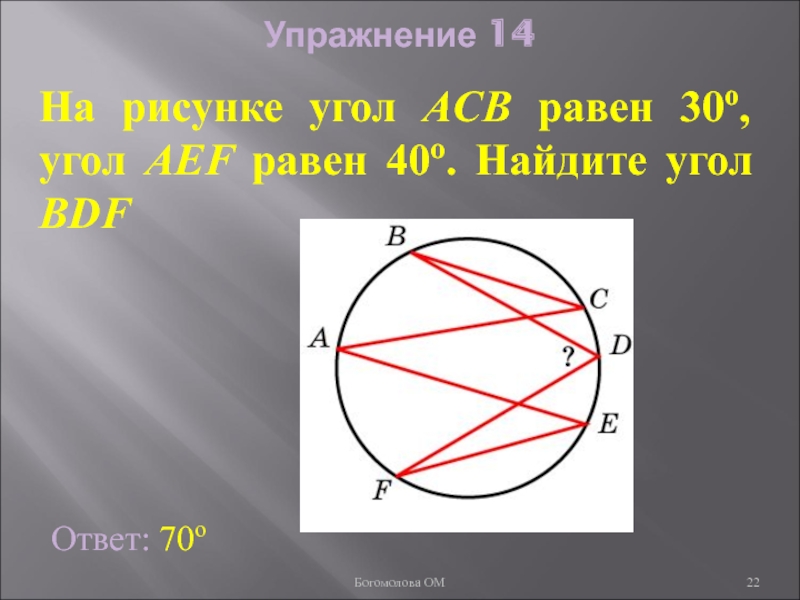
Слайд 22Упражнение 14
На рисунке угол ACB равен 30о, угол AEF равен 40о.
Ответ: 70о
Богомолова ОМ
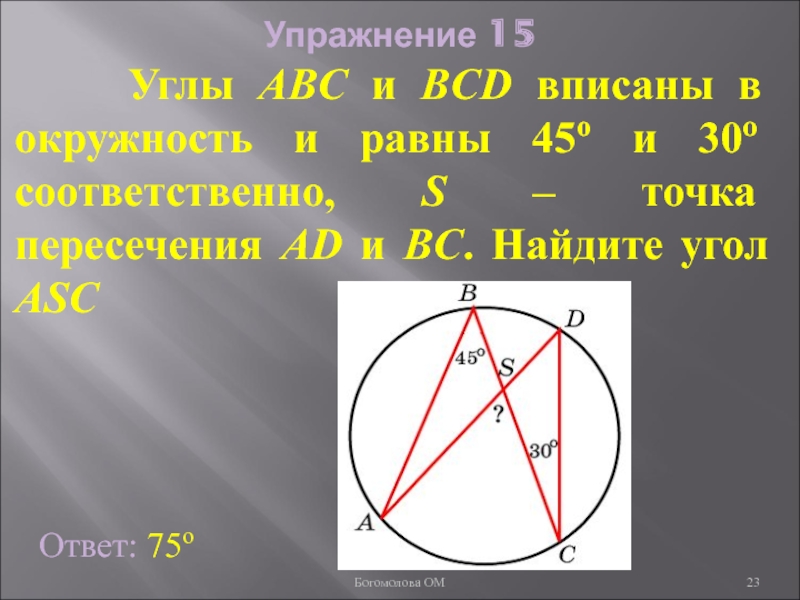
Слайд 23Упражнение 15
Углы ABC и BCD вписаны в окружность
Ответ: 75о
Богомолова ОМ
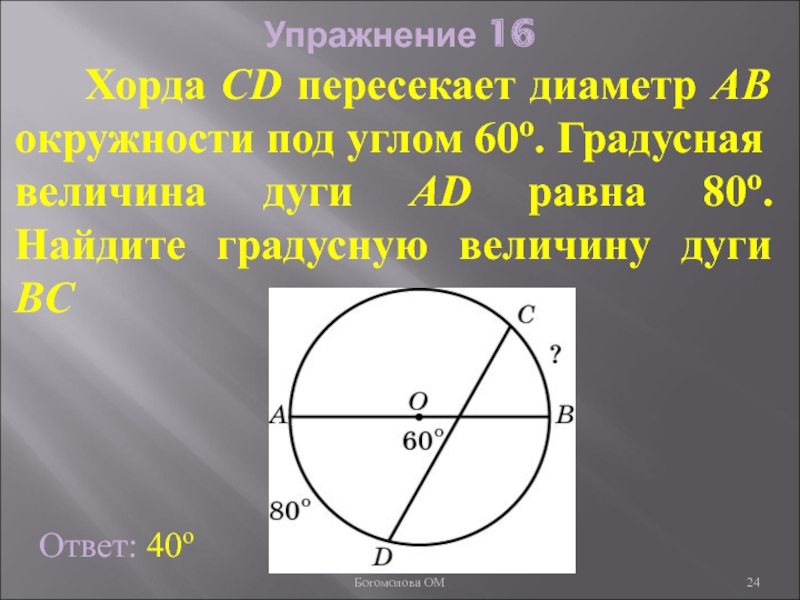
Слайд 24Упражнение 16
Хорда CD пересекает диаметр AB окружности под
Ответ: 40о
Богомолова ОМ
Слайд 25Упражнение 17
На рисунке угол A равен 40о, угол
Ответ: 115о
Богомолова ОМ
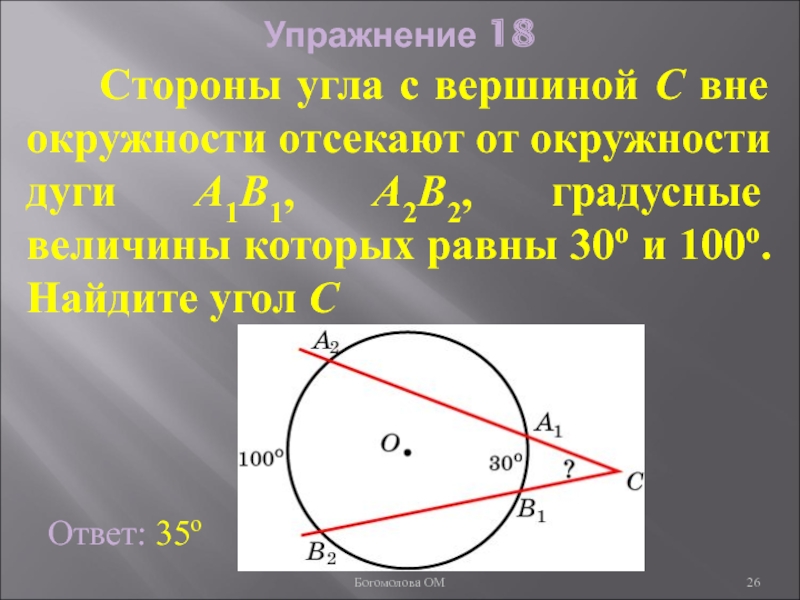
Слайд 26Упражнение 18
Стороны угла с вершиной C вне окружности
Ответ: 35о
Богомолова ОМ
Слайд 27Упражнение 19
Углы ABC и BCD вписаны в окружность
Ответ: 30о
Богомолова ОМ
Слайд 28Упражнение 20
Стороны угла с вершиной C вне окружности
Ответ: 40о
Богомолова ОМ
Слайд 29Упражнение 21
Через концы дуги в 60о проведены касательные, пересекающиеся
Ответ: 120о
Богомолова ОМ
Слайд 30Упражнение 22
Хорда АВ стягивает дугу окружности в 44о.
Ответ: 22о
Богомолова ОМ
Слайд 31Упражнение 23
Две равные окружности расположены таким образом, что
Ответ: 120о
Богомолова ОМ
Слайд 32Упражнение 24
Острый вписанный угол опирается на хорду, которая
Ответ: 80о
Богомолова ОМ
Слайд 33Упражнение 25
Ответ: 90о
Точки А, В, С, расположенные
Богомолова ОМ
Слайд 34Упражнение 26
Ответ: 105о
Точки А, В, С, расположенные на
Богомолова ОМ
Слайд 35Упражнение 27
Окружность разделена точками A, B, C, D
Ответ: 60о
Богомолова ОМ
Слайд 36Упражнение 28
В четырехугольнике ABCD, вписанном в окружность, угол
Ответ: 15о
Богомолова ОМ
Слайд 37Упражнение 29
Углы A и C вписанного в окружность
Ответ: 40о
Богомолова ОМ
Слайд 38Упражнение 30
На рисунке угол A равен 120о,
Ответ: 130о
Богомолова ОМ
Слайд 39Упражнение 31
Хорда CD перпендикулярна радиусу OB окружности и пересекает
Ответ: 60о
Богомолова ОМ
Слайд 40Упражнение 32
Окружность разделена точками A, B, C, D
Ответ: 80о
Богомолова ОМ
Слайд 41Упражнение 33
Окружность разделена точками A, B, C, D
Ответ: 36о
Богомолова ОМ
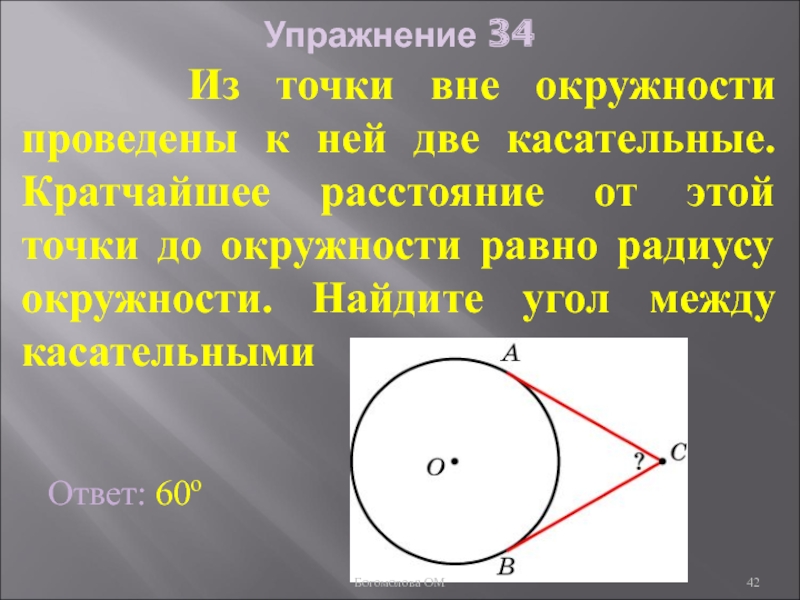
Слайд 42Упражнение 34
Из точки вне окружности проведены к ней
Ответ: 60о
Богомолова ОМ
Слайд 43Упражнение 35
В угол АСB вписана окружность. Точки касания
Ответ: 36о
Богомолова ОМ
Слайд 44Упражнение 36
В угол АСB, величиной 50о, вписана окружность. Точки
Ответ: 230о
Богомолова ОМ
Слайд 45Упражнение 37
В угол АСB, величиной 45о, вписана окружность.
Ответ: 3:5
Богомолова ОМ
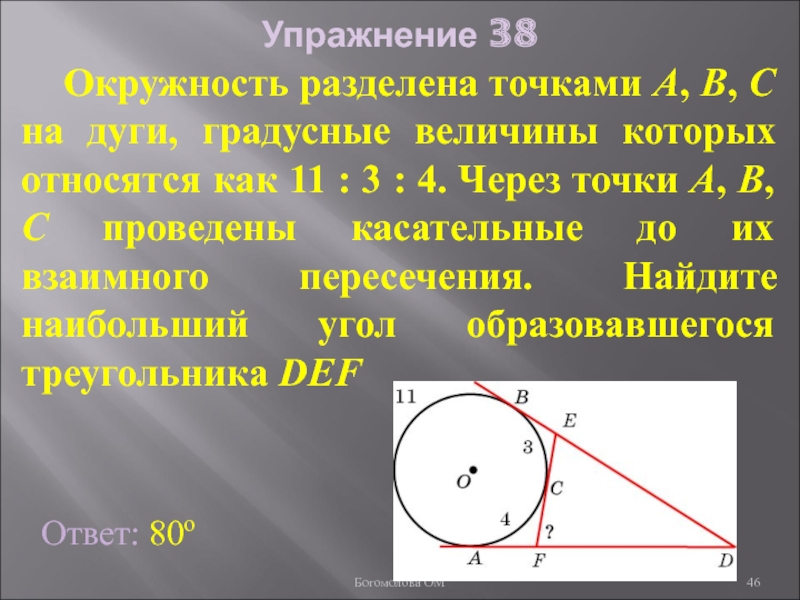
Слайд 46Упражнение 38
Окружность разделена точками А, В, С на дуги,
Ответ: 80о
Богомолова ОМ
Слайд 47Упражнение 39
Треугольник ABC вписан в окружность. Угол A
Ответ: 20о
Богомолова ОМ
Слайд 48Упражнение 40
Треугольник ABC вписан в окружность. Угол A
Ответ: 20о
Богомолова ОМ
Слайд 49Упражнение 41
Стороны четырехугольника ABCD касаются окружности в точках,
Ответ: 70о
Богомолова ОМ
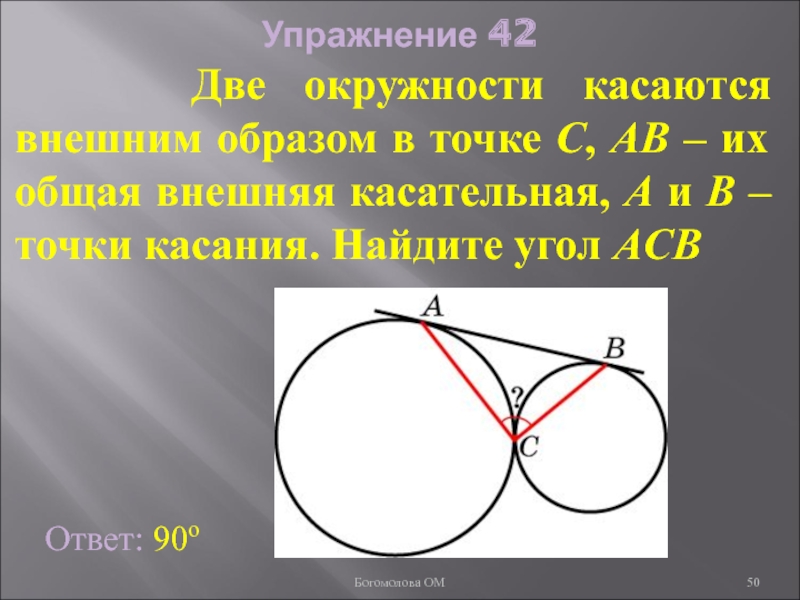
Слайд 50Упражнение 42
Две окружности касаются внешним образом в точке
Ответ: 90о
Богомолова ОМ