- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Непрерывность функции в точке и на отрезке презентация
Содержание
- 1. Непрерывность функции в точке и на отрезке
- 2. Непрерывность функции в точке Определение 1:
- 3. Непрерывность функции в точке Определение 2:
- 4. Непрерывность функции в точке Определение 3:
- 5. Графическая интерпретация: Основы математического анализа Автор:
- 6. Свойства функций, непрерывных в точке 1.
- 7. 4. Непрерывность сложной функции Пусть функция
- 8. 4. Непрерывность сложной функции: Следствие Основы
- 9. Пример 3: Решение: Установить непрерывность или
- 10. 1. Устранимый разрыв Основы математического анализа
- 11. 2. Разрыв 1-го рода Основы математического
- 12. 3. Разрыв 2-го рода Основы математического
- 13. Пример 4: Решение: Найти точки разрыва
- 14. Односторонняя непрерывность функции в точке Основы
- 15. Односторонняя непрерывность функции в точке Непрерывность
- 16. Определение: Основы математического анализа Автор:
- 17. Свойства функций, непрерывных на отрезке Функция
- 18. Свойства функций, непрерывных на отрезке Основы
- 19. Свойства функций, непрерывных на отрезке Основы
- 20. Непрерывность обратной функции Основы математического анализа
- 21. Непрерывность обратной функции Основы математического анализа
- 22. Высшая математика Автор: И.В.Дайняк, к.т.н., доцент кафедры высшей математики БГУИР math.mmts-it.org
Слайд 1НЕПРЕРЫВНОСТЬ ФУНКЦИИ
В ТОЧКЕ И НА ОТРЕЗКЕ
Тема 7
Основы математического анализа
Автор: И.
Слайд 2
Непрерывность функции в точке
Определение 1:
Функция f (x) называется непрерывной в точке
Запись через односторонние пределы:
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Слайд 3
Непрерывность функции в точке
Определение 2:
Функция f (x) называется непрерывной в точке
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Слайд 4
Непрерывность функции в точке
Определение 3:
Функция f (x) называется непрерывной в точке
– приращение аргумента
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Обозначения:
– приращение функции
Слайд 5
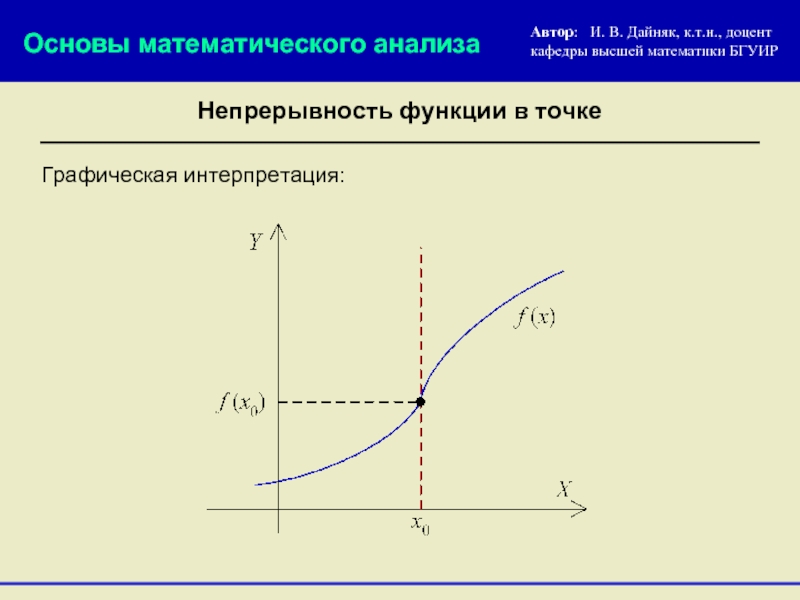
Графическая интерпретация:
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей
Непрерывность функции в точке
Слайд 6
Свойства функций, непрерывных в точке
1. Функция, непрерывная в точке х0, ограничена
3. Если функции f (x) и g(x) непрерывны в точке x0, то функции:
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
2. Если функция непрерывная в точке х0, то существует некоторая окрестность U(x0), в которой функция имеет такой же знак, как и f (x0).
тоже непрерывны в точке x0
Слайд 7
4. Непрерывность сложной функции
Пусть функция g(x) непрерывна в точке x0, а
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Свойства функций, непрерывных в точке
Доказательство:
Следовательно,
Слайд 8
4. Непрерывность сложной функции: Следствие
Основы математического анализа
Автор: И. В. Дайняк,
Свойства функций, непрерывных в точке
Таким образом, знак предела и знак непрерывной функции можно менять местами.
Метод замены переменной для пределов непрерывных функций:
Слайд 9
Пример 3:
Решение:
Установить непрерывность или разрывность функции
Ответ:
Основы математического анализа
Автор: И. В.
Непрерывность функции в точке
Слайд 10
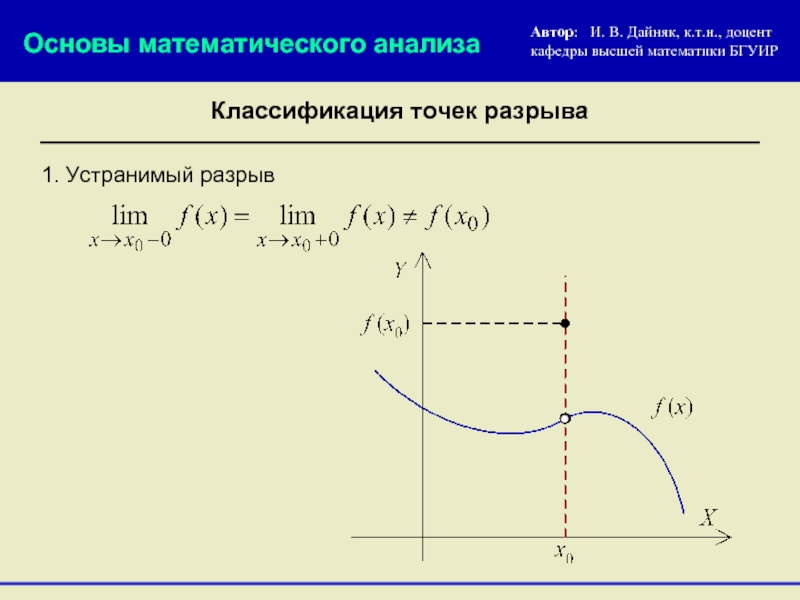
1. Устранимый разрыв
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры
Классификация точек разрыва
Слайд 11
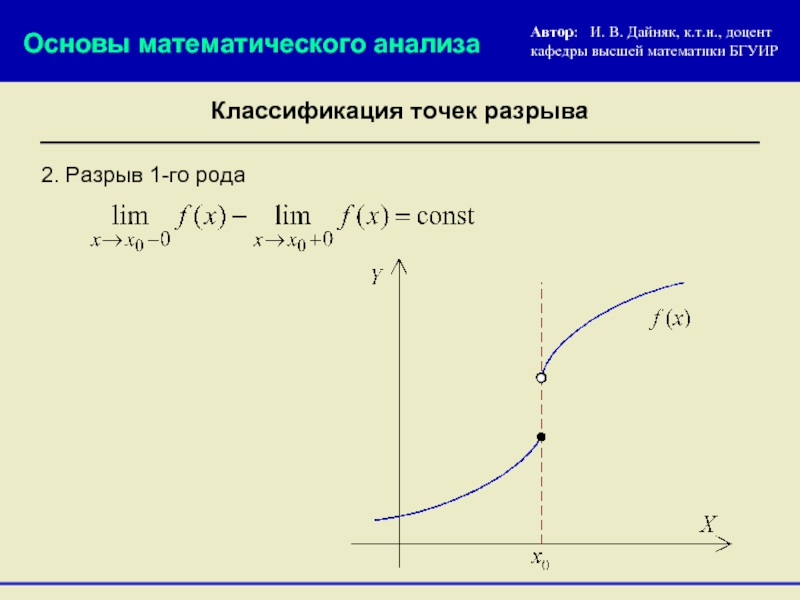
2. Разрыв 1-го рода
Основы математического анализа
Автор: И. В. Дайняк, к.т.н.,
Классификация точек разрыва
Слайд 12
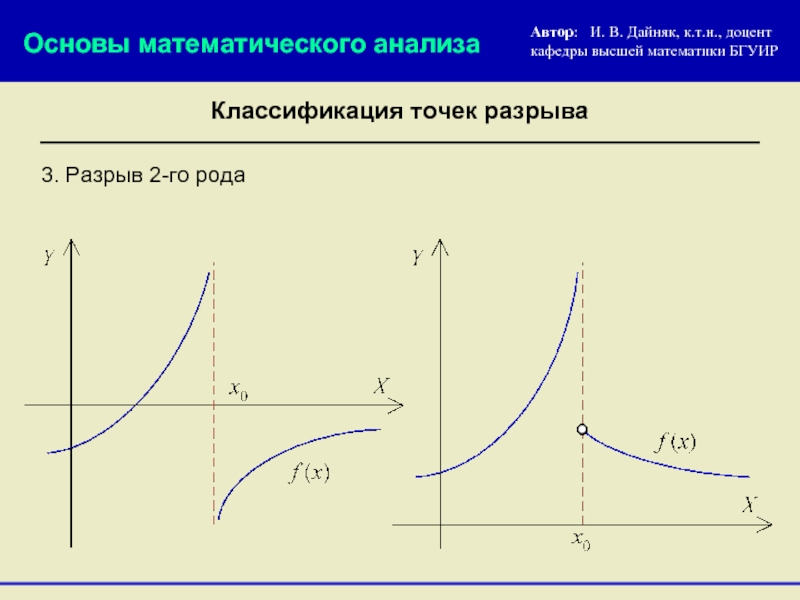
3. Разрыв 2-го рода
Основы математического анализа
Автор: И. В. Дайняк, к.т.н.,
Классификация точек разрыва
Слайд 13
Пример 4:
Решение:
Найти точки разрыва функции и установить их характер
Ответ:
Основы математического анализа
Автор:
Непрерывность функции в точке
Слайд 14
Односторонняя непрерывность функции в точке
Основы математического анализа
Автор: И. В. Дайняк,
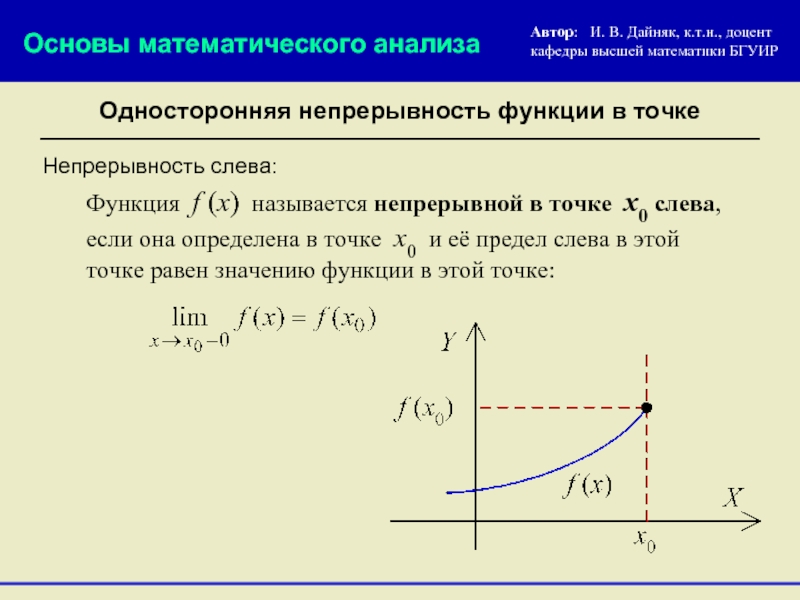
Непрерывность слева:
Функция f (x) называется непрерывной в точке х0 слева, если она определена в точке x0 и её предел слева в этой точке равен значению функции в этой точке:
Слайд 15
Односторонняя непрерывность функции в точке
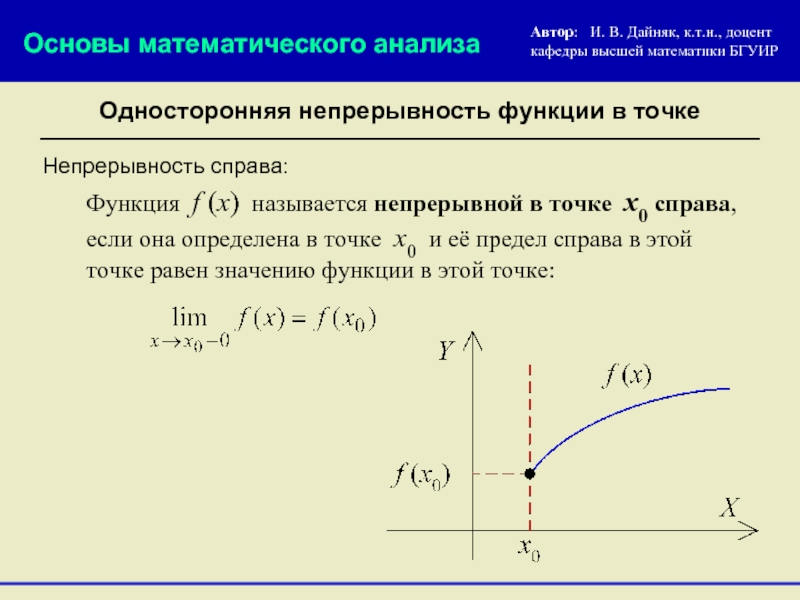
Непрерывность справа:
Функция f (x) называется непрерывной в
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Слайд 16
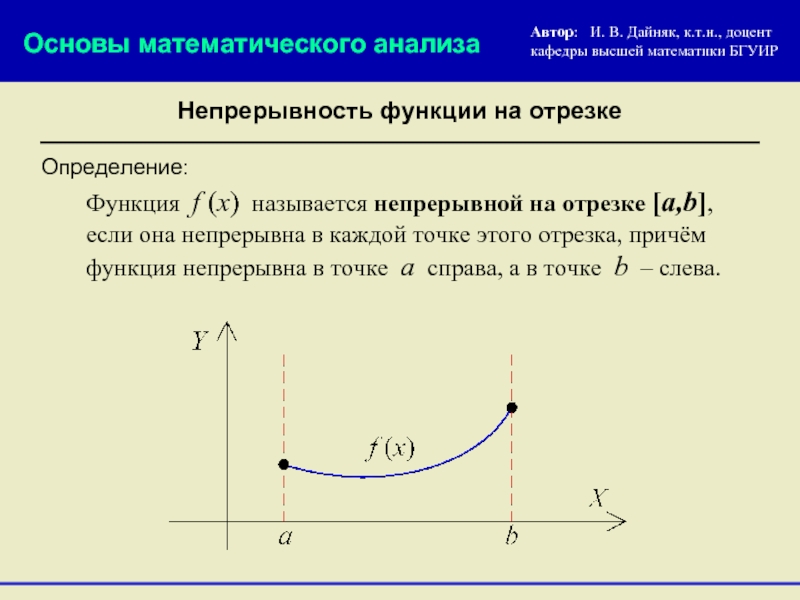
Определение:
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики
Непрерывность функции на отрезке
Функция f (x) называется непрерывной на отрезке [a,b], если она непрерывна в каждой точке этого отрезка, причём функция непрерывна в точке a справа, а в точке b – слева.
Слайд 17
Свойства функций, непрерывных на отрезке
Функция f (x), непрерывная на отрезке [a,
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры высшей математики БГУИР
Теорема 1 (Вейерштрасса):
Теорема 2 (Вейерштрасса):
Функция f (x), непрерывная на отрезке [a, b], достигает на этом отрезке своих точной верхней и точной нижней граней.
Слайд 18
Свойства функций, непрерывных на отрезке
Основы математического анализа
Автор: И. В. Дайняк,
Если функция f (x) непрерывна на отрезке [a, b] и на концах его принимает значения A= f (a) и B = f (b) разных знаков, то внутри отрезка [a, b] найдётся по крайней мере одна точка х = с, для которой f (c) = 0.
Теорема (Коши о прохождении функции через ноль):
Слайд 19
Свойства функций, непрерывных на отрезке
Основы математического анализа
Автор: И. В. Дайняк,
Если функция f (x) непрерывна на отрезке [a, b] и f (a) = А,
f (b) = В, то для любого числа С, удовлетворяющего неравенству А < С < В, на интервале (a, b) найдётся такая точка х = с, для которой f (c) = С.
Теорема (Коши о промежуточном значении):
Слайд 20
Непрерывность обратной функции
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры
Функция f (x) называется строго возрастающей на отрезке
[a, b], если для любых двух чисел x1 и x2, принадлежащих интервалу [a, b], из неравенства x1 < x2 следует неравенство f (x1) < f (x2).
Определение 1:
Определение 2:
Функция f (x) называется строго убывающей на отрезке
[a, b], если для любых двух чисел x1 и x2, принадлежащих интервалу [a, b], из неравенства x1 < x2 следует неравенство f (x1) > f (x2).
Слайд 21
Непрерывность обратной функции
Основы математического анализа
Автор: И. В. Дайняк, к.т.н., доцент
кафедры
Если функция f (x) строго монотонна и непрерывна на отрезке [a, b] и интервал [A, B] – множество её значений, то существует обратная функция f –1, являющаяся строго монотонной.
Теорема 1:
Теорема 2:
Если функция f (x) строго монотонна и непрерывна на отрезке [a, b], то обратная функция f –1 непрерывна на отрезке [A, B], где [A, B] – множество значений
функции f (x).









![Свойства функций, непрерывных на отрезкеФункция f (x), непрерывная на отрезке [a, b], ограничена на нём.Основы](/img/tmb/2/144411/284bbeb1799c7a19c7ab3c6897e22aa1-800x.jpg)