- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции и их свойства. План проведения занятия презентация
Содержание
- 1. Функции и их свойства. План проведения занятия
- 2. Скуднева Оксана Валентиновна Образование: МГТУ им. Н.
- 3. Основные понятия и определения. Закон, ставящий каждому
- 4. Способы задания функции 1) табличный
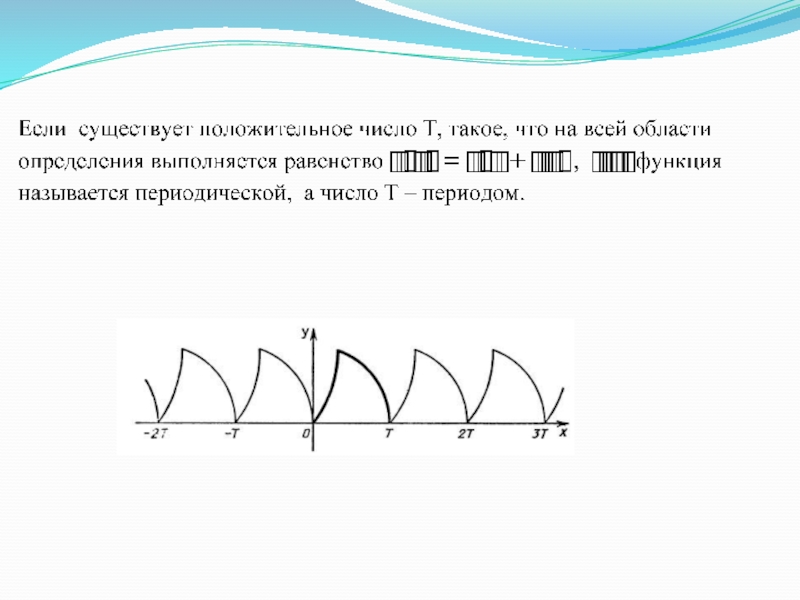
- 5. Если область определения функции D(f) симметрична относительно
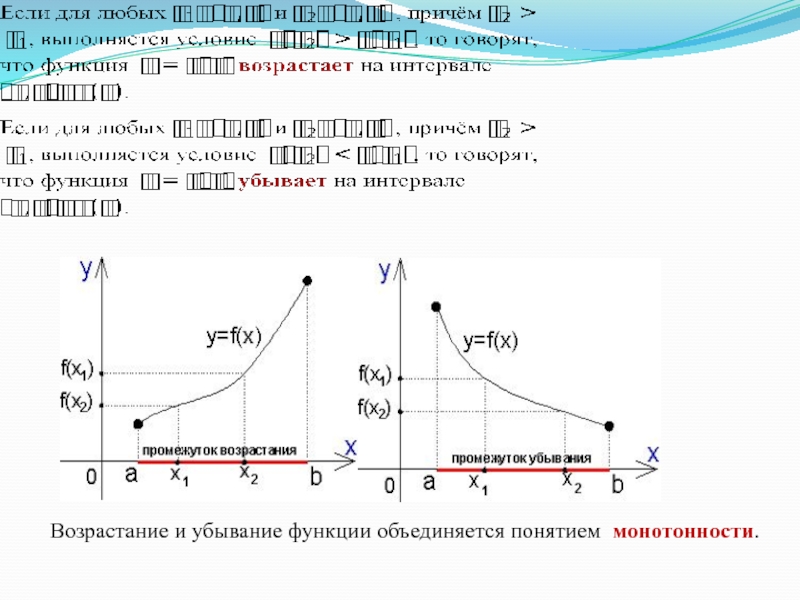
- 6. . Возрастание и убывание функции объединяется понятием монотонности.
- 7. Если на промежутке области определения функция имеет
- 9. Ограниченные функции. Пример. Функция, ограниченная сверху: Функция,
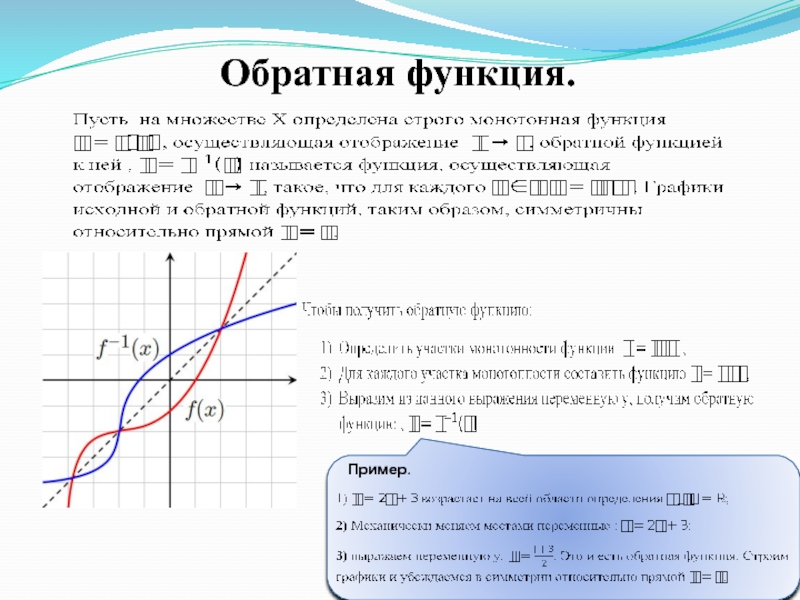
- 10. Обратная функция. Пример.
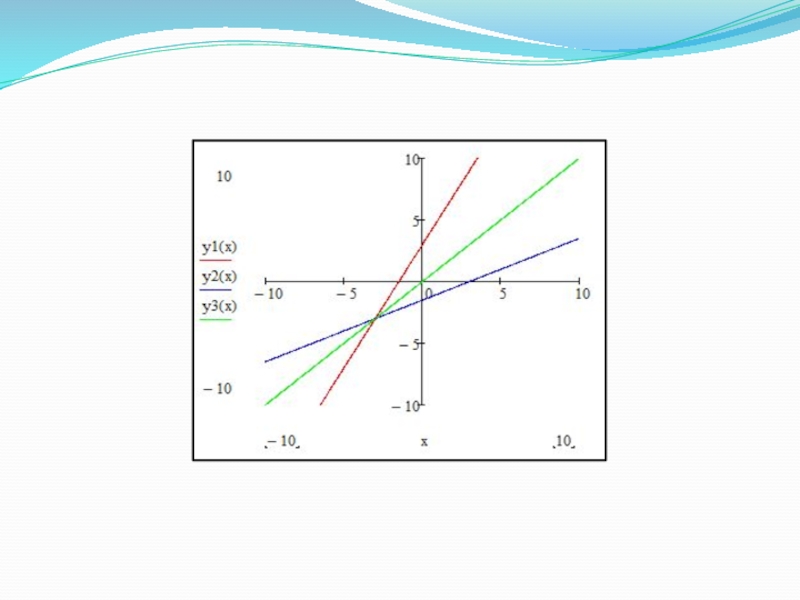
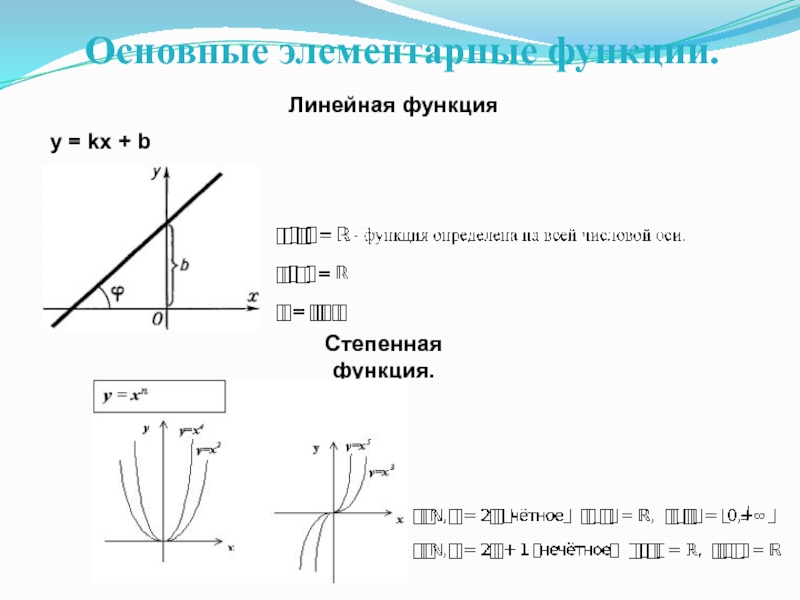
- 12. Основные элементарные функции. Линейная функция Степенная функция. y = kx + b
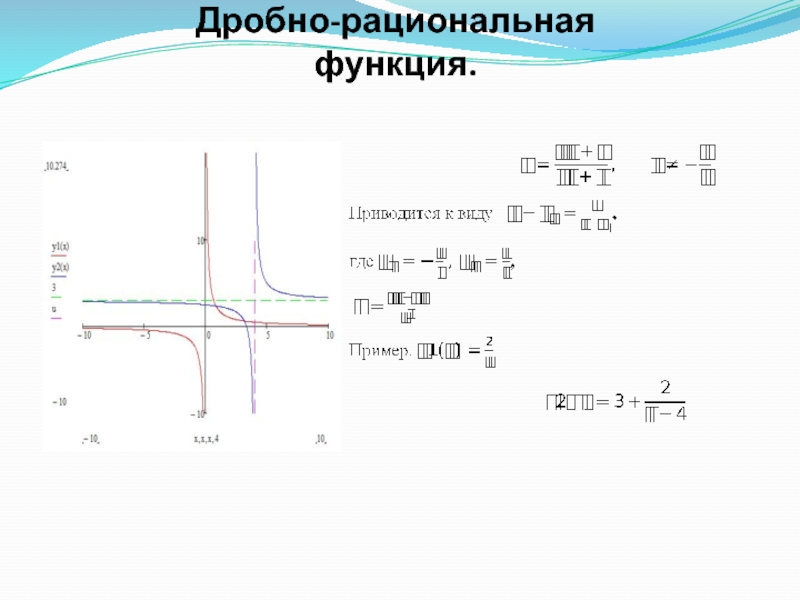
- 13. Дробно-рациональная функция.
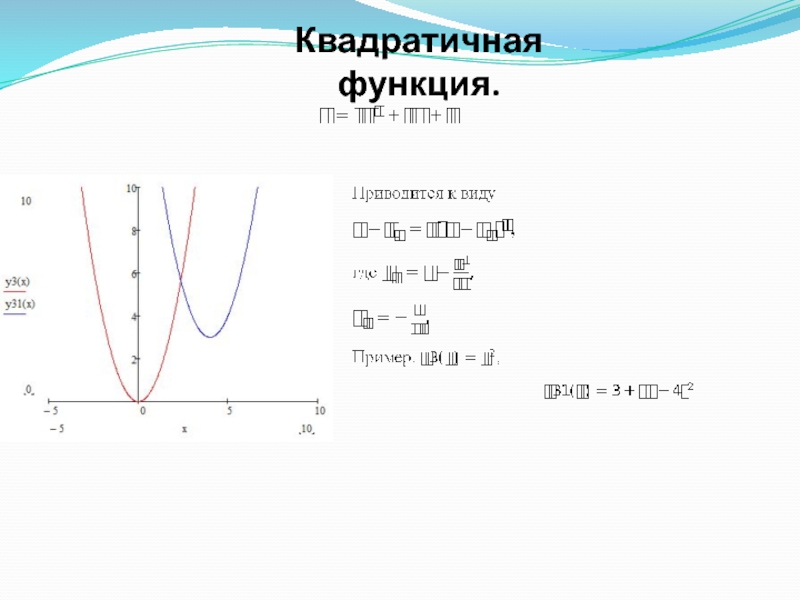
- 14. Квадратичная функция.
- 15. Степенные функции с рациональным показателем. В зависимости
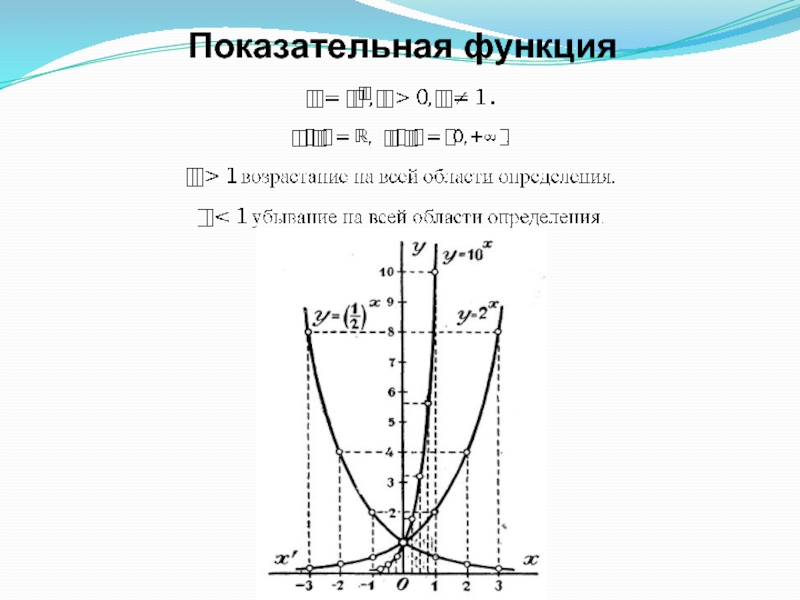
- 16. Показательная функция
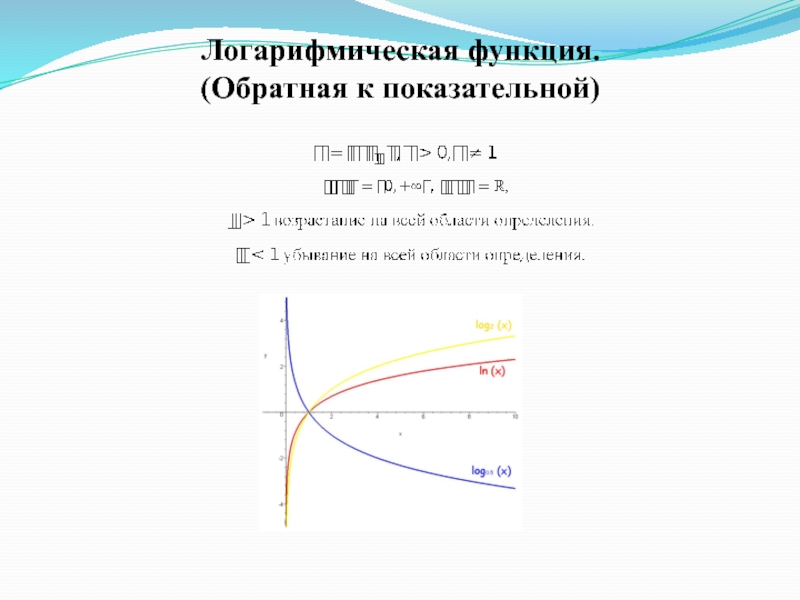
- 17. Логарифмическая функция. (Обратная к показательной)
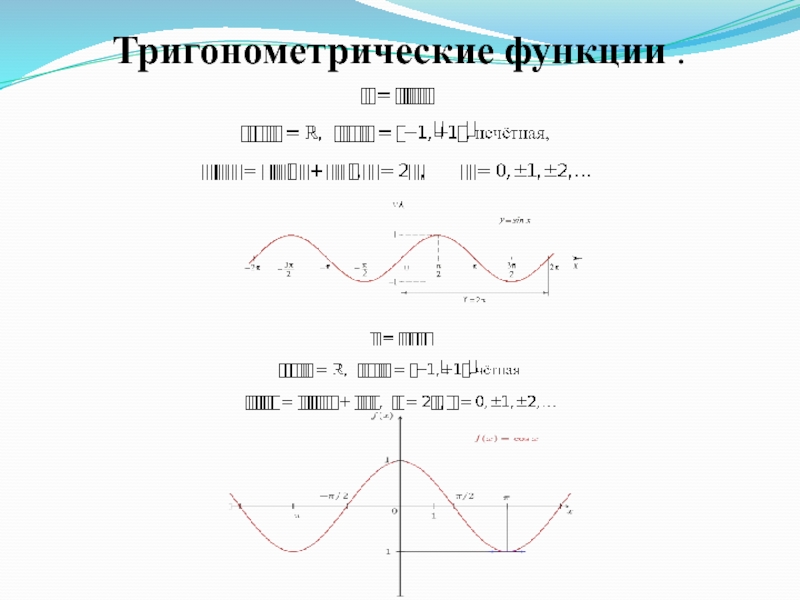
- 18. Тригонометрические функции .
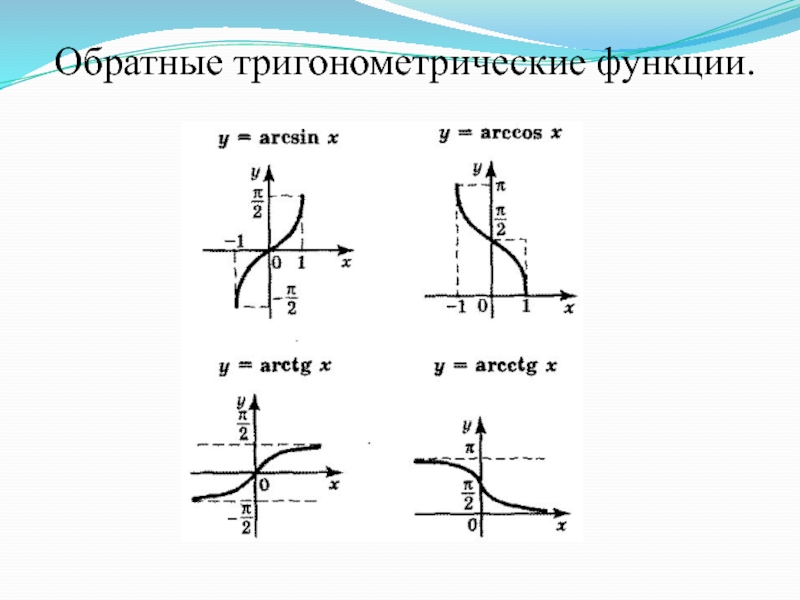
- 20. Обратные тригонометрические функции.
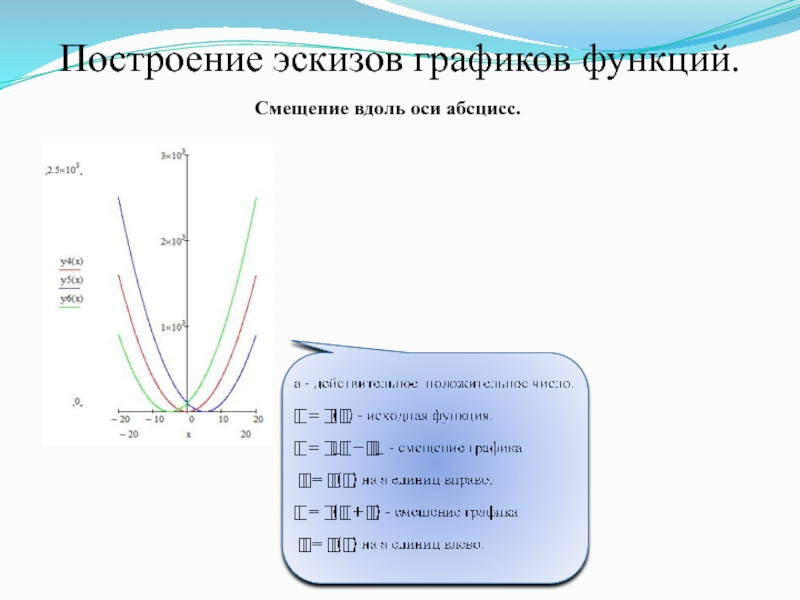
- 21. Построение эскизов графиков функций. Смещение вдоль оси абсцисс.
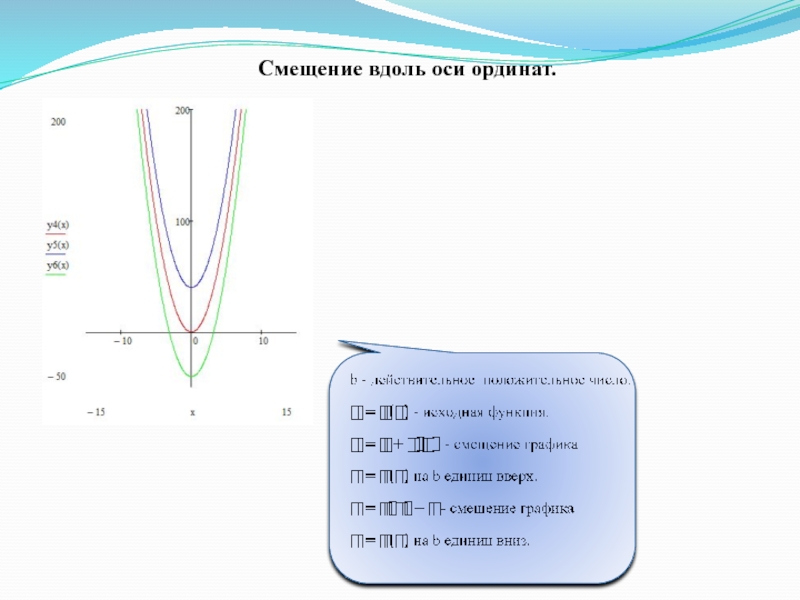
- 22. Смещение вдоль оси ординат.
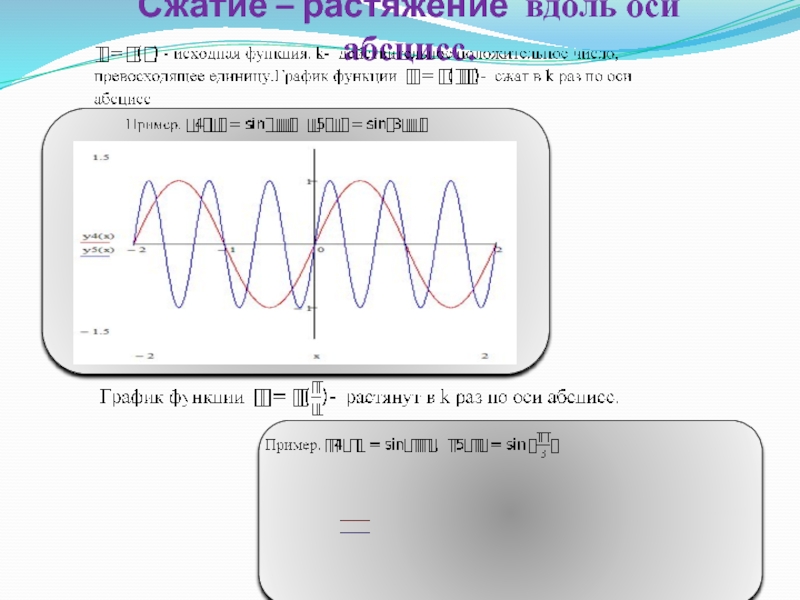
- 23. Сжатие – растяжение вдоль оси абсцисс.
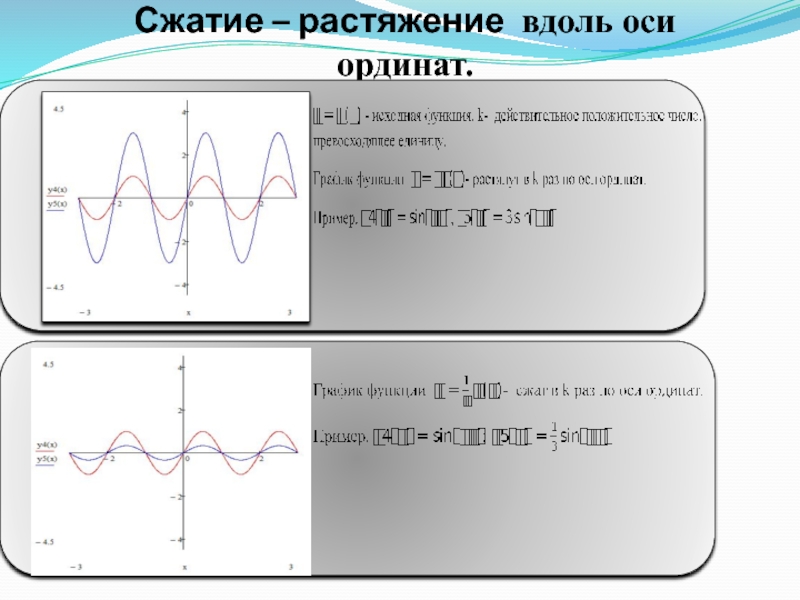
- 24. Сжатие – растяжение вдоль оси ординат.
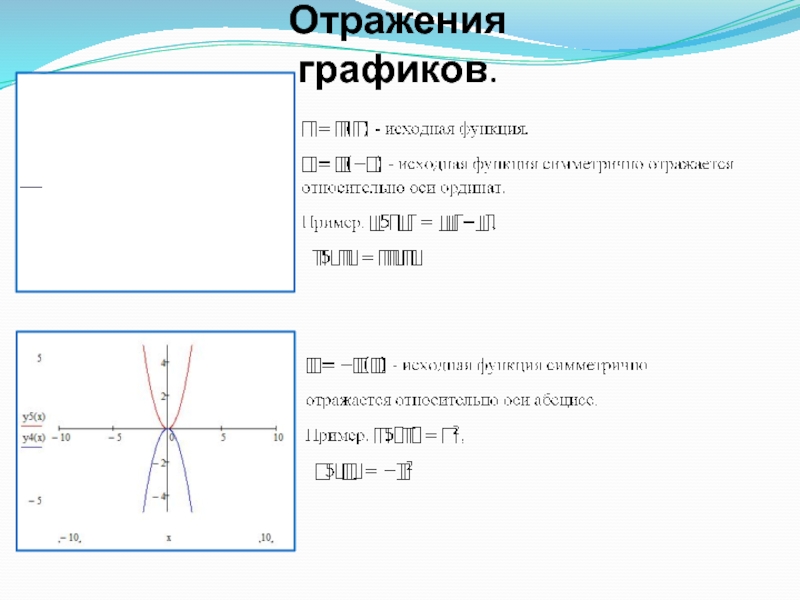
- 25. Отражения графиков.
Скуднева Оксана Валентиновна Образование: МГТУ им. Н. Э. Баумана, специальность «Системы автоматического управления»; МГУ им. М. В. Ломоносова, специальность «Математика. Прикладная математика». Место работы: МГТУ им. Н. Э. Баумана, НУК ФН,
Слайд 2Скуднева Оксана Валентиновна
Образование: МГТУ им. Н. Э. Баумана, специальность «Системы автоматического
управления»;
МГУ им. М. В. Ломоносова, специальность «Математика. Прикладная математика».
Место работы: МГТУ им. Н. Э. Баумана, НУК ФН, кафедра «Вычислительная математика и математическая физика», должность – старший преподаватель.
Опыт работы: средняя школа, 2002-2011 гг., факультативные курсы по подготовке к Олимпиадам МГТУ им. Н. Э. Баумана «Шаг в будущее», «Олимпиада Жуковского», ЕГЭ по математике, основной курс алгебры физ-мат. класса.
МГУ им. М. В. Ломоносова, специальность «Математика. Прикладная математика».
Место работы: МГТУ им. Н. Э. Баумана, НУК ФН, кафедра «Вычислительная математика и математическая физика», должность – старший преподаватель.
Опыт работы: средняя школа, 2002-2011 гг., факультативные курсы по подготовке к Олимпиадам МГТУ им. Н. Э. Баумана «Шаг в будущее», «Олимпиада Жуковского», ЕГЭ по математике, основной курс алгебры физ-мат. класса.
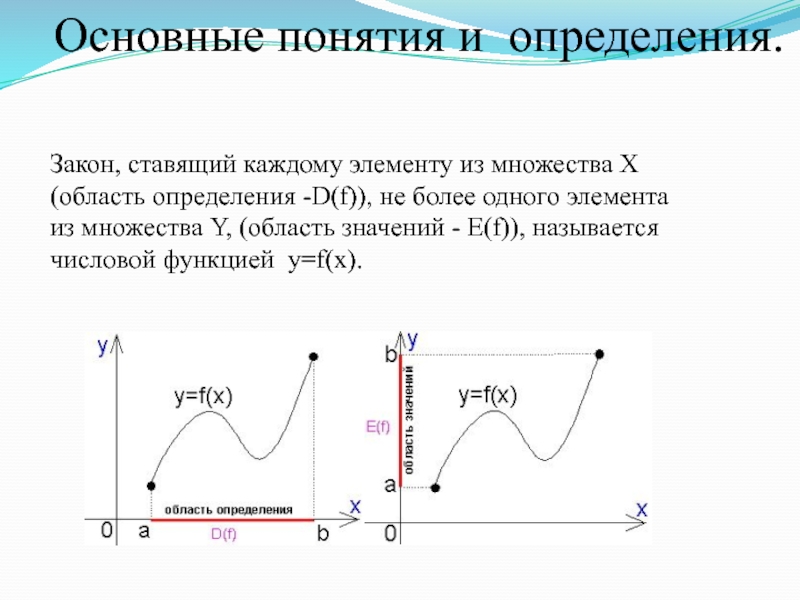
Слайд 3Основные понятия и определения.
Закон, ставящий каждому элементу из множества X (область
определения -D(f)), не более одного элемента из множества Y, (область значений - E(f)), называется числовой функцией y=f(x).
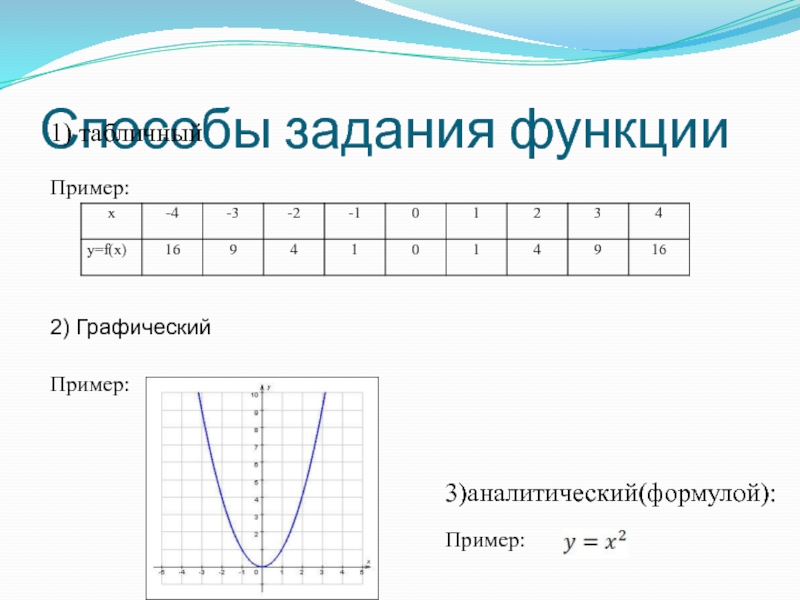
Слайд 4Способы задания функции
1) табличный
Пример:
2) Графический
Пример:
3)аналитический(формулой):
Пример:
Слайд 5Если область определения функции D(f) симметрична относительно начала координат, и для
каждого значения xϵ D(f) выполняется условие f(-x)=f(x), функция называется чётной. График чётной функции симметричен относительно оси OY.
Если область определения функции D(f) симметрична относительно начала координат, и для каждого значения xϵ D(f) выполняется условие f(-x)=-f(x), функция называется нечётной. График нечётной функции симметричен относительно начала координат.
Если область определения функции D(f) симметрична относительно начала координат, и для каждого значения xϵ D(f) выполняется условие f(-x)=-f(x), функция называется нечётной. График нечётной функции симметричен относительно начала координат.
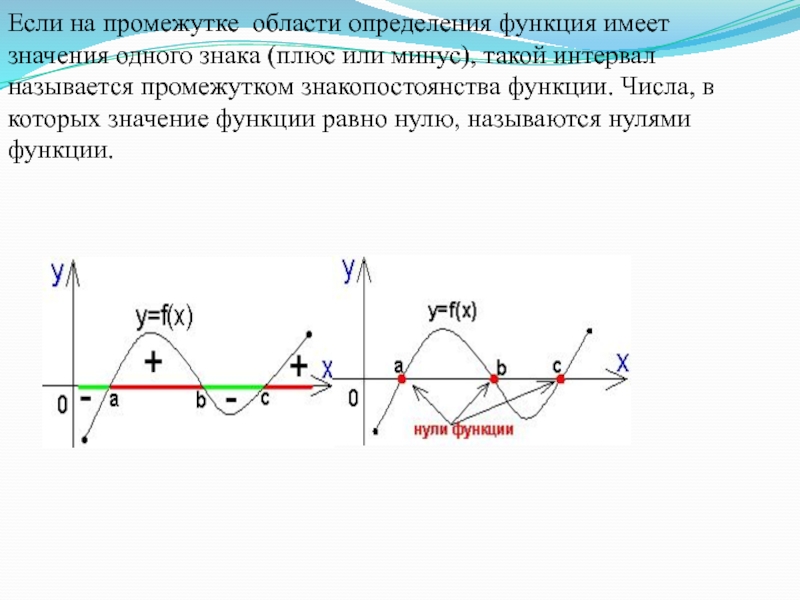
Слайд 7Если на промежутке области определения функция имеет значения одного знака (плюс
или минус), такой интервал называется промежутком знакопостоянства функции. Числа, в которых значение функции равно нулю, называются нулями функции.
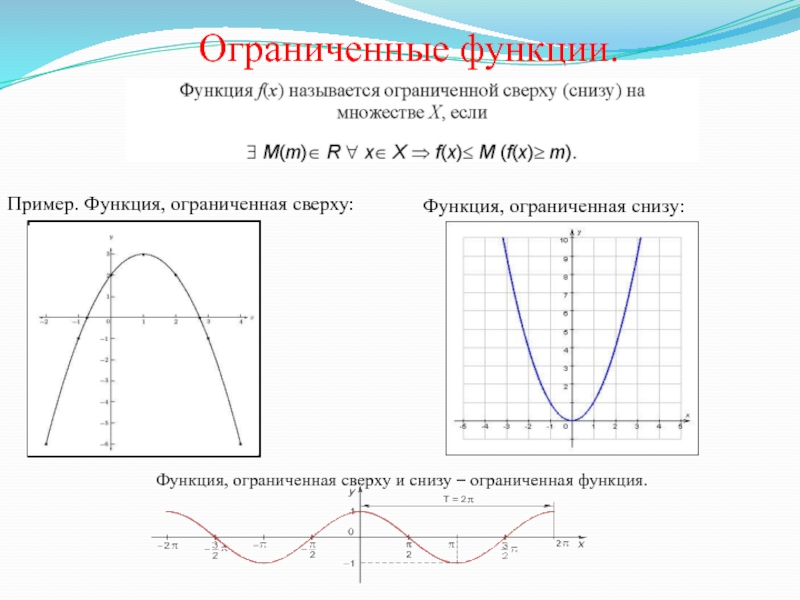
Слайд 9Ограниченные функции.
Пример. Функция, ограниченная сверху:
Функция, ограниченная снизу:
Функция, ограниченная сверху и снизу
– ограниченная функция.
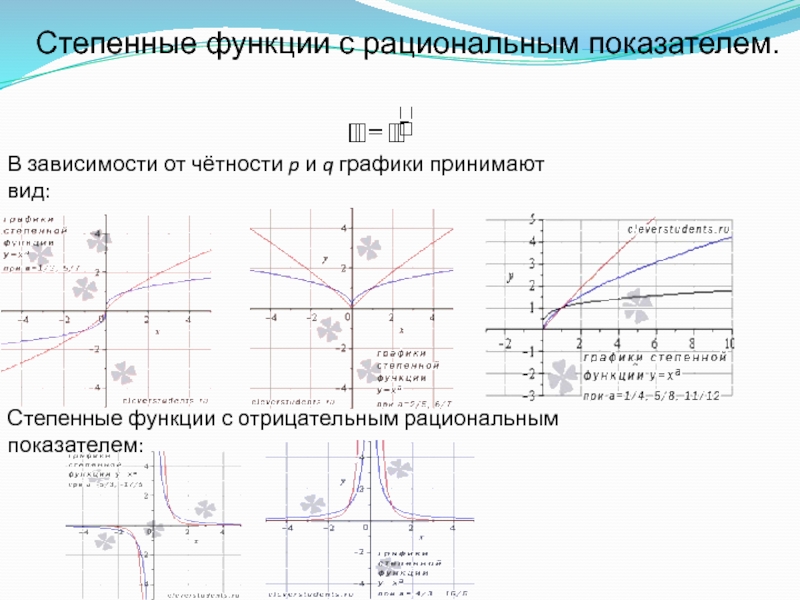
Слайд 15Степенные функции с рациональным показателем.
В зависимости от чётности p и q
графики принимают вид:
Степенные функции с отрицательным рациональным показателем:
