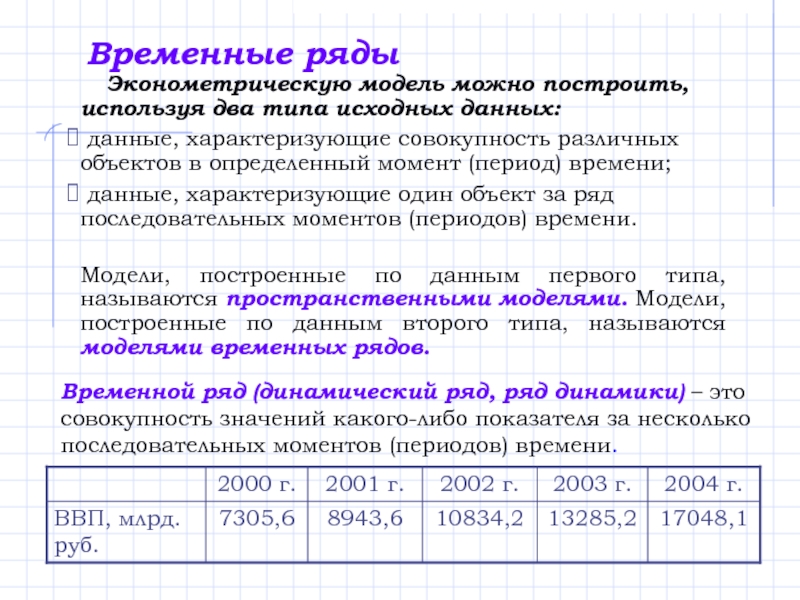
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема о равенстве односторонних углов. Теорема о свойстве односторонних углов презентация
Содержание
- 1. Теорема о равенстве односторонних углов. Теорема о свойстве односторонних углов
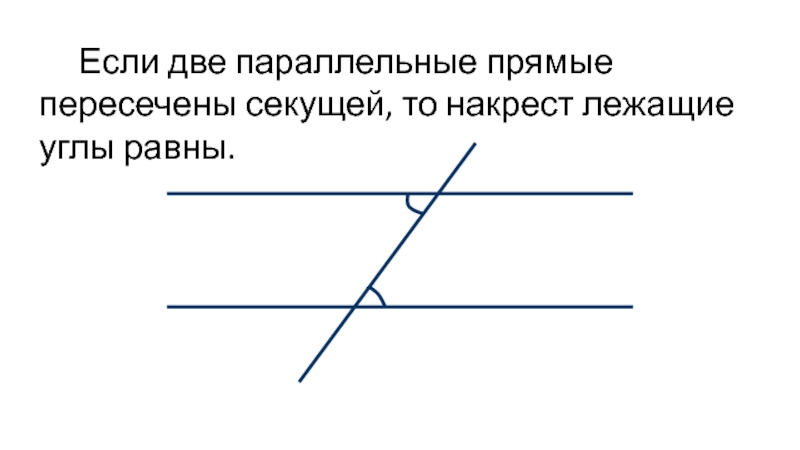
- 2. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
- 3. Теорема. Если две параллельные прямые пересечены секущей,
- 4. А В С D M N
- 5. Теорема. Если две параллельные прямые пересечены секущей,
- 6. А В С D E ∠ BAD + ∠ ADE = 180°
- 7. Задача. Луч BD – биссектриса ∠ АВС,
- 8. Задача. Градусная мера одного из внутренних односторонних
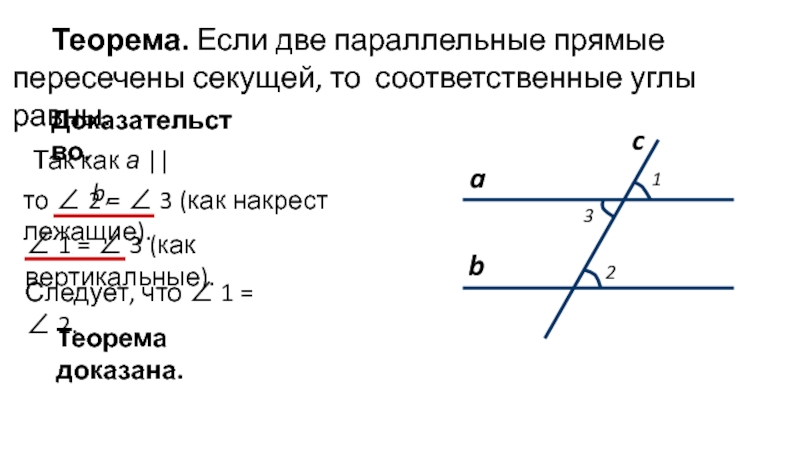
Слайд 3Теорема. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Доказательство.
a
b
c
1
2
3
Так
то ∠ 2 = ∠ 3 (как накрест лежащие).
∠ 1 = ∠ 3 (как вертикальные).
Следует, что ∠ 1 = ∠ 2.
Теорема доказана.
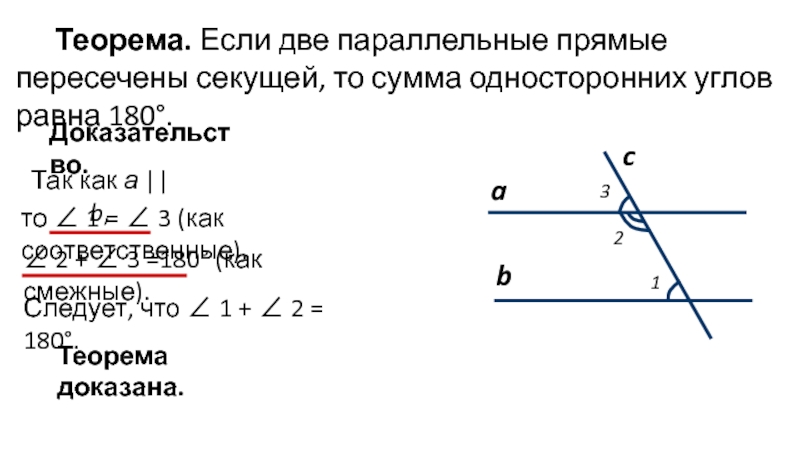
Слайд 5Теорема. Если две параллельные прямые пересечены секущей, то сумма односторонних углов
Доказательство.
a
b
c
1
2
3
Так как а || b,
то ∠ 1 = ∠ 3 (как соответственные).
∠ 2 + ∠ 3 =180° (как смежные).
Следует, что ∠ 1 + ∠ 2 = 180°.
Теорема доказана.
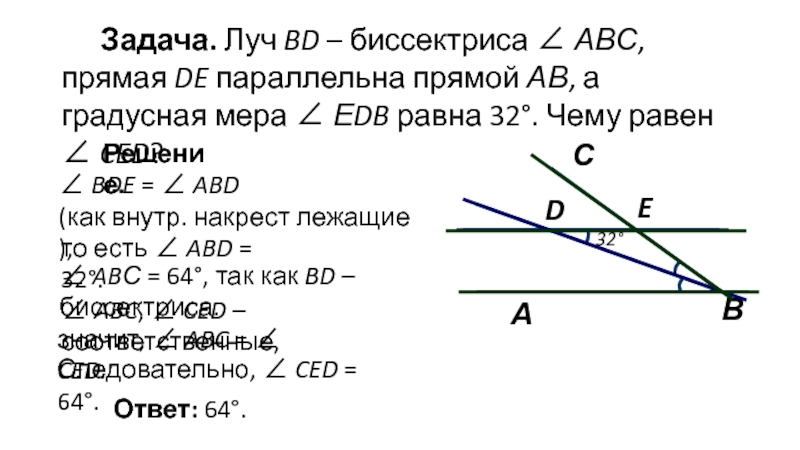
Слайд 7Задача. Луч BD – биссектриса ∠ АВС, прямая DE параллельна прямой
Решение.
А
В
С
D
E
∠ BDE = ∠ ABD
(как внутр. накрест лежащие ),
то есть ∠ ABD = 32°.
32°
∠ ABС = 64°, так как BD – биссектриса.
∠ ABC, ∠ CED – соответственные,
значит, ∠ ABC = ∠ CED.
Следовательно, ∠ CED = 64°.
Ответ: 64°.
Слайд 8Задача. Градусная мера одного из внутренних односторонних углов, образованных при пересечении
Решение.
a
b
c
1
2
то ∠ 1 + ∠ 2 = 180°.
Получаем ∠ 1 = 103°,
∠ 2 = 77°.
Ответ: 103°, 77°.