- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Чисельні методи. Елементи теорії похибок. (Лекція 1) презентация
Содержание
- 1. Чисельні методи. Елементи теорії похибок. (Лекція 1)
- 2. Лекція №1 Елементи теорії похибок
- 3. План лекції: І. Класифікація чисельних методів ІІ.
- 4. Література: Бахвалов Н.С. Численные методы, М.
- 5. Програмне забезпечення 1. Основне: 1. MATHCAD (www.mathsoft.com)
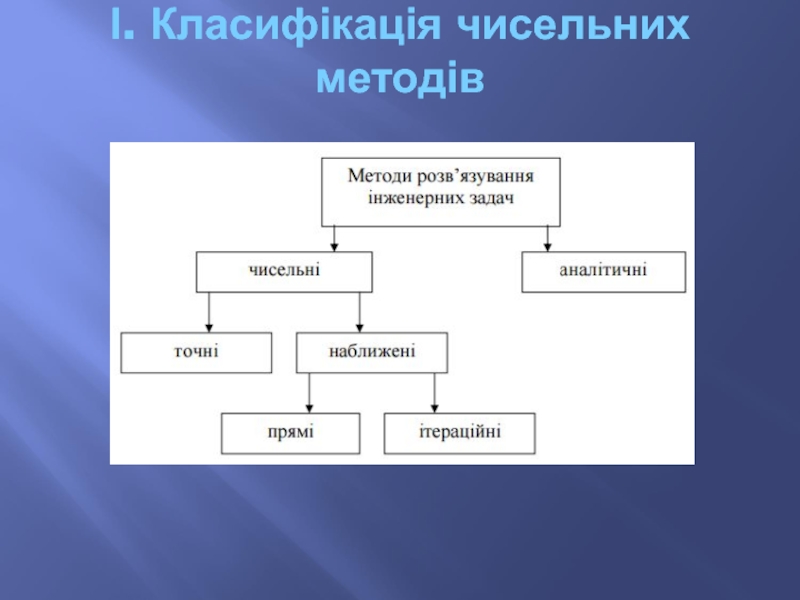
- 6. І. Класифікація чисельних методів
- 7. ІІ. Елементи теорії похибок 1. Класифікація похибок
- 8. Приклад Коливання фізичного маятника L
- 9. 2. Форми представлення чисел в ЕОМ
- 10. 2. числа з плаваючою комою q=2, t=36, p0=64 ; /p/ < p0
- 11. 3. Абсолютна та відносна похибки Нехай
- 12. Якщо наближене значення деякої величини записане у
Слайд 3План лекції:
І. Класифікація чисельних методів
ІІ. Елементи теорії похибок
1. Класифікація похибок
2. Числа з фіксованою та плаваючою комою
3. Абсолютна та відносна похибки
Слайд 4Література:
Бахвалов Н.С. Численные методы, М. Наука, 1975.
Волков Е.А. Численные методы,
М. Наука, 1982.
Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике, 1990
Крылов В.И., Бобков В.В., Монастырный П. Н., Вычислительные методы
Поттер Д. Вычислительные методы в физике , М.Мир,1975.
Демидович Б.П., Марон И.А., Основы вычислительной математики, М. Наука, 1970.
Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике, 1990
Крылов В.И., Бобков В.В., Монастырный П. Н., Вычислительные методы
Поттер Д. Вычислительные методы в физике , М.Мир,1975.
Демидович Б.П., Марон И.А., Основы вычислительной математики, М. Наука, 1970.
Слайд 5Програмне забезпечення
1. Основне:
1. MATHCAD (www.mathsoft.com)
2. MS EXCEL
Додаткове:
3. MATLAB (www.mathworks.com)
4. MAPLE
(www.maplesoft.com)
5. MATHEMATICA (www.wolfram.com
5. MATHEMATICA (www.wolfram.com
Слайд 7ІІ. Елементи теорії похибок
1. Класифікація похибок
Похибки результату розв’язку задачі зумовлені
наступними причинами:
Математичний опис задачі є неточним
(неусунена похибка )
Наближені методи розв’язку
(похибка методу)
Числові дані та результати обчислень округлюють
(обчислювальна похибка)
18,34461≈18,345≈18,35
Математичний опис задачі є неточним
(неусунена похибка )
Наближені методи розв’язку
(похибка методу)
Числові дані та результати обчислень округлюють
(обчислювальна похибка)
18,34461≈18,345≈18,35
Слайд 8Приклад
Коливання фізичного маятника
L
ϕ
L d2ϕ/dt2 + g sinϕ + μ dϕ/dt =
0
L- довжина маятника
- кут відхилення від вертикалі
μ - коефіцієнт тертя
Слайд 92. Форми представлення чисел в ЕОМ
Сучасні ЕОМ оперують числами, що мають
наступні форми запису :
числа з фіксованою комою
(α, q-цілі / q - основа системи числення: q=2, 8, 10, 16)
числа з фіксованою комою
(α, q-цілі / q - основа системи числення: q=2, 8, 10, 16)
Слайд 113. Абсолютна та відносна похибки
Нехай а – точне значення деякої величини;
а*
- наближене значення величини а. Тоді величина
а- а* =ε називається похибкою,
∆(a*)=│а- а* │-абсолютною похибкою, а
- відносною похибкою,
а- а* =ε називається похибкою,
∆(a*)=│а- а* │-абсолютною похибкою, а
- відносною похибкою,
Слайд 12Якщо наближене значення деякої величини записане у десятковій системі числення, то
гранична абсолютна похибка дорівнює одиниці останнього знаку (якщо значення одержане без округлення) та половині одиниці останнього знаку (якщо значення одержане з округленням).
Останнім знаком вважають перший з права.
Останнім знаком вважають перший з права.