- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
свойства соответствий презентация
Содержание
- 1. свойства соответствий
- 2. Образ элемента Образом элемента ХϵХ при соответствии
- 3. Образ элемента 1ϵX – элемент аϵY Иначе
- 4. Прообразом элемента уϵУ при соответствии G=
- 5. Прообраз элемента fϵY – элемент 3ϵX Иначе
- 6. ОПРЕДЕЛИТЕ образы элементов Х соответствия G= и прообразы элементов Z соответствия D=.
- 7. Соответствия и отношения Основные свойства соответствий
- 8. Соответствие G= называется функциональным, если образ любого
- 9. В противном случае соответствие является нефункциональным, т.е.
- 10. В случае, если каждому элементу хϵХ соответствует
- 11. Соответствие G= называется инъективным, если, прообраз
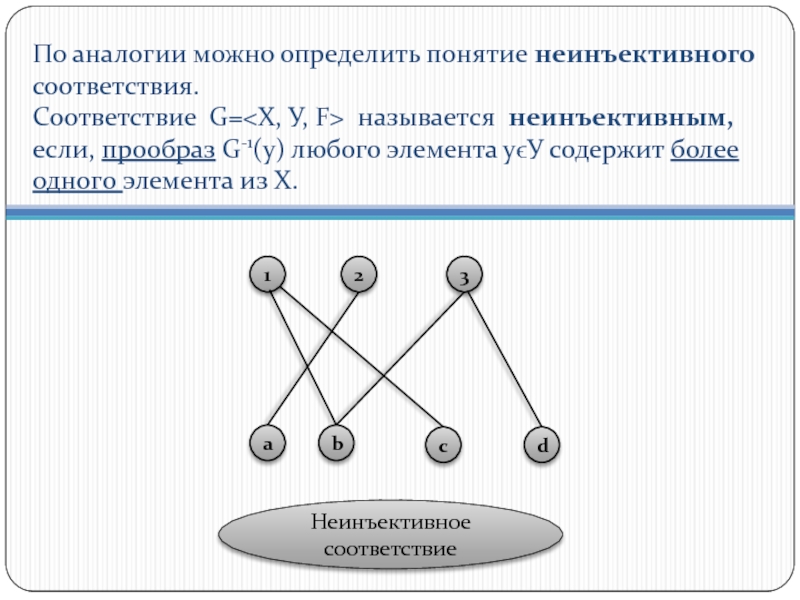
- 12. По аналогии можно определить понятие неинъективного
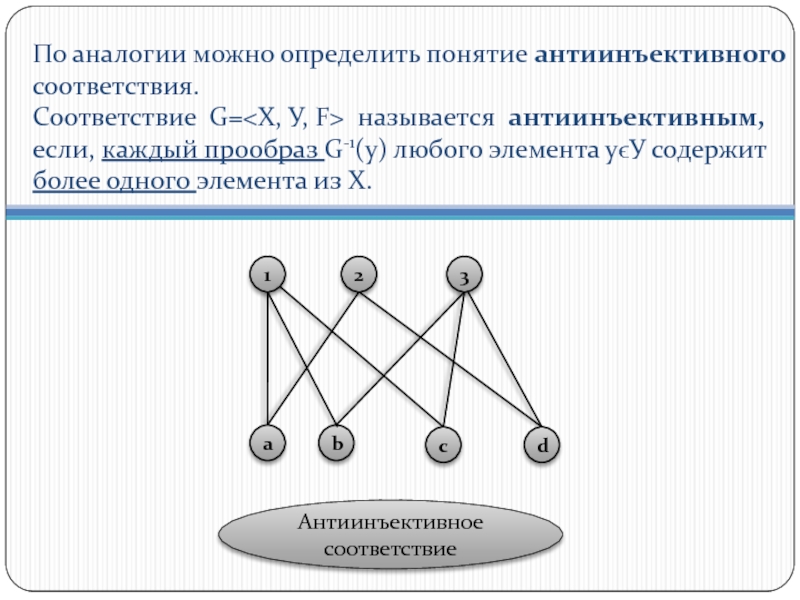
- 13. По аналогии можно определить понятие антиинъективного
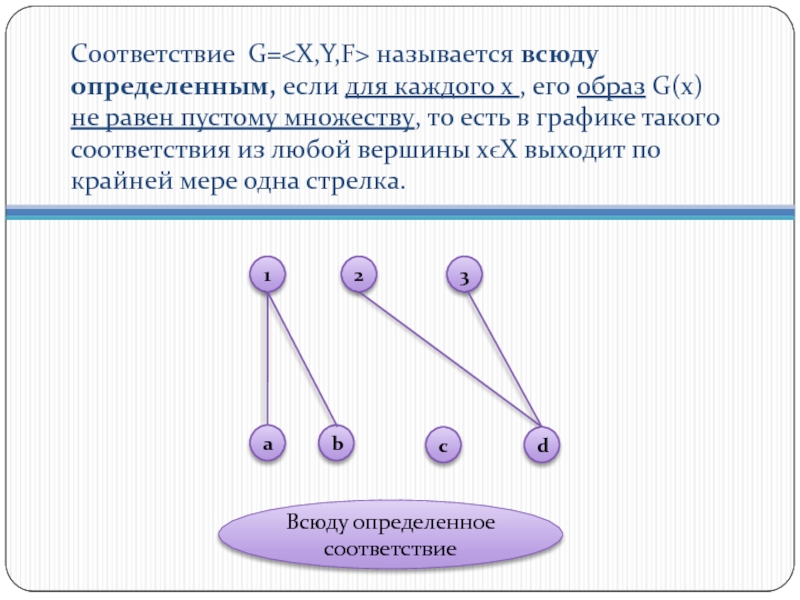
- 14. Соответствие G= называется всюду определенным, если для
- 15. В противном случае соответствие является не всюду определенным. Не всюду определенное соответствие
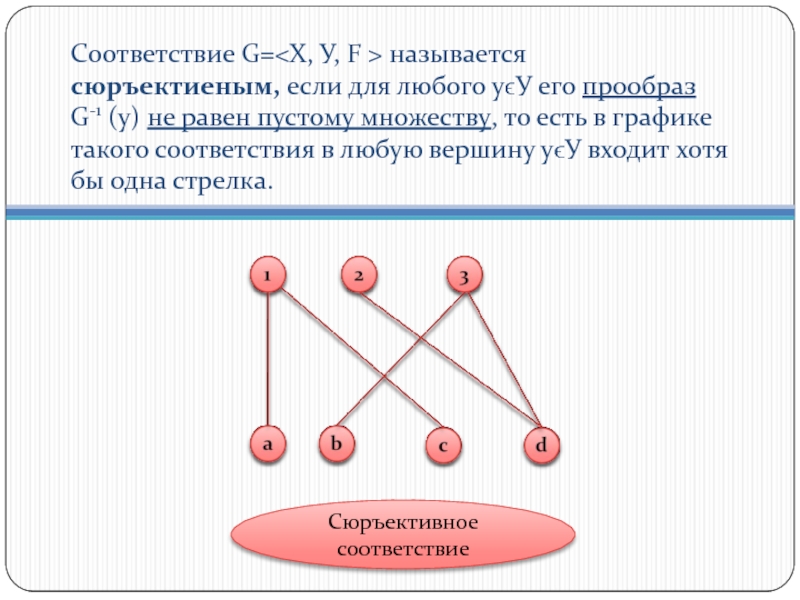
- 16. Соответствие G= называется сюръектиеным, если для любого
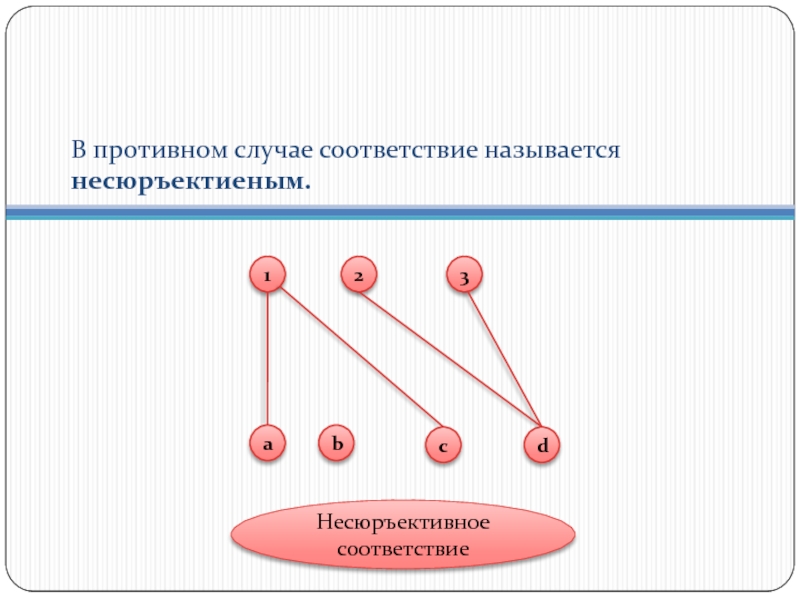
- 17. В противном случае соответствие называется несюръектиеным. Несюръективное соответствие
- 18. Соответствие называется биективным или взаимооднозначным, если оно
- 19. Нефункциональное соответствие Всюду определенное соответствие Антиинъективное соответствие Сюръективное соответствие Определите свойства соответствий
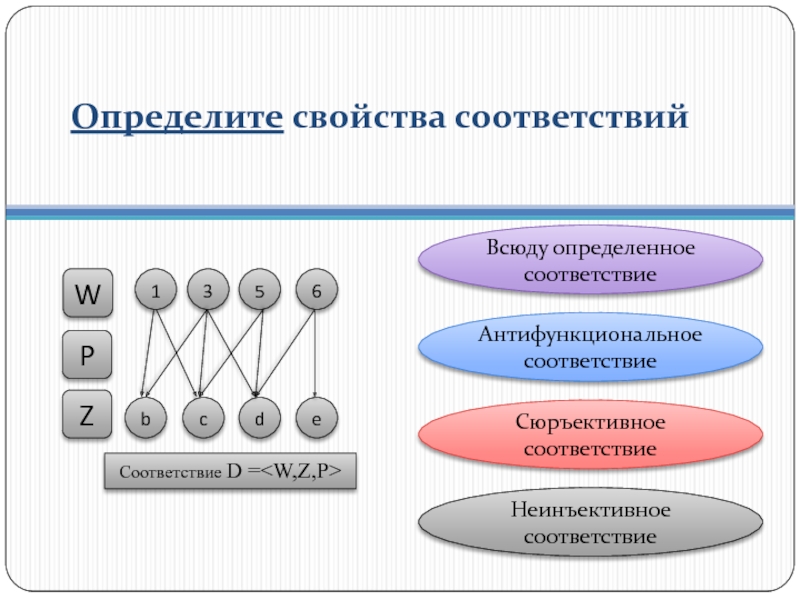
- 20. Определите свойства соответствий Антифункциональное соответствие Всюду определенное соответствие Неинъективное соответствие Сюръективное соответствие
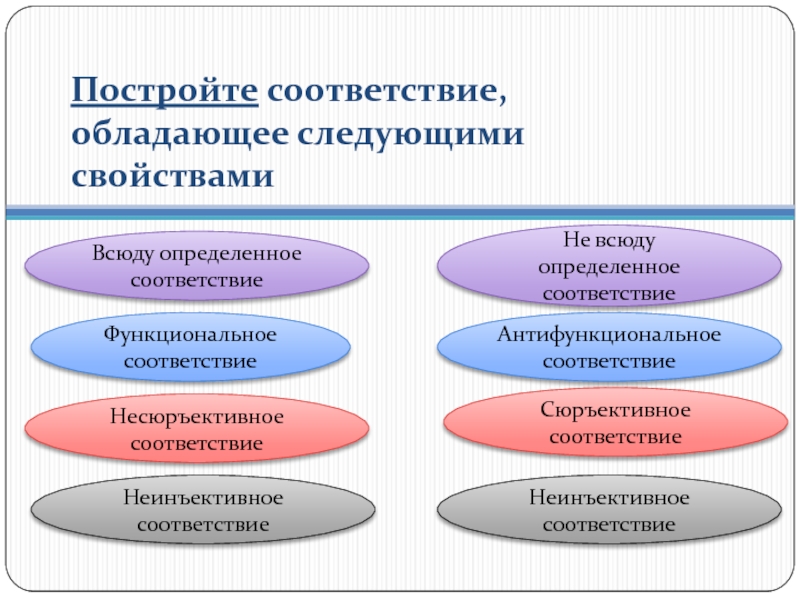
- 21. Постройте соответствие, обладающее следующими свойствами Функциональное соответствие
- 22. Домашнее задание: записать свойства соответствий, чертежи
Слайд 2Образ элемента
Образом элемента ХϵХ при соответствии G= называется множество
Иначе говоря, образ элемента х при соответствии G - это множество всех стрелок, выходящих из х.
Слайд 3Образ элемента 1ϵX – элемент аϵY
Иначе говоря, образ элемента х при
Слайд 4Прообразом элемента уϵУ при соответствии G= называется множество элементов хϵХ,
Прообраз элемента
-1
Иначе говоря, прообраз элемента х при соответствии G - это множество стрелок, входящих в элемент у.
Слайд 5Прообраз элемента fϵY – элемент 3ϵX
Иначе говоря, прообраз элемента х при
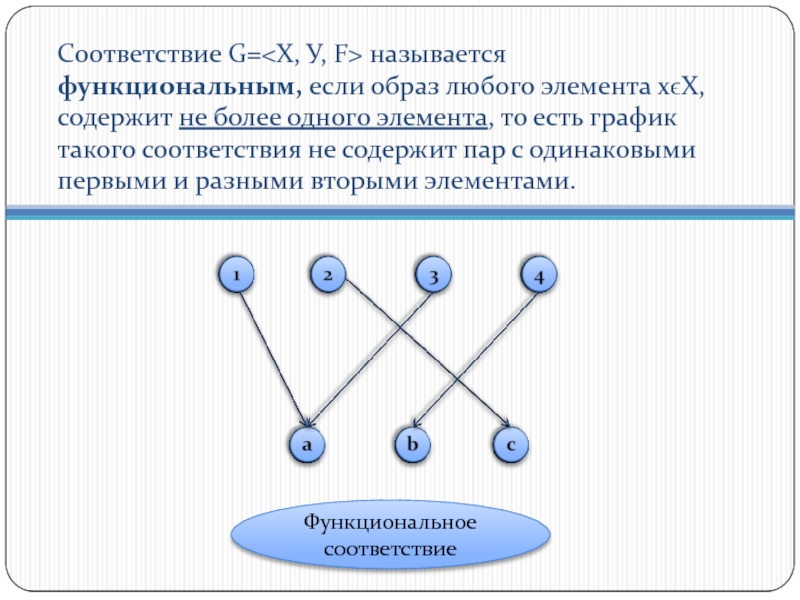
Слайд 8Соответствие G= называется функциональным, если образ любого элемента хϵХ,
Функциональное соответствие
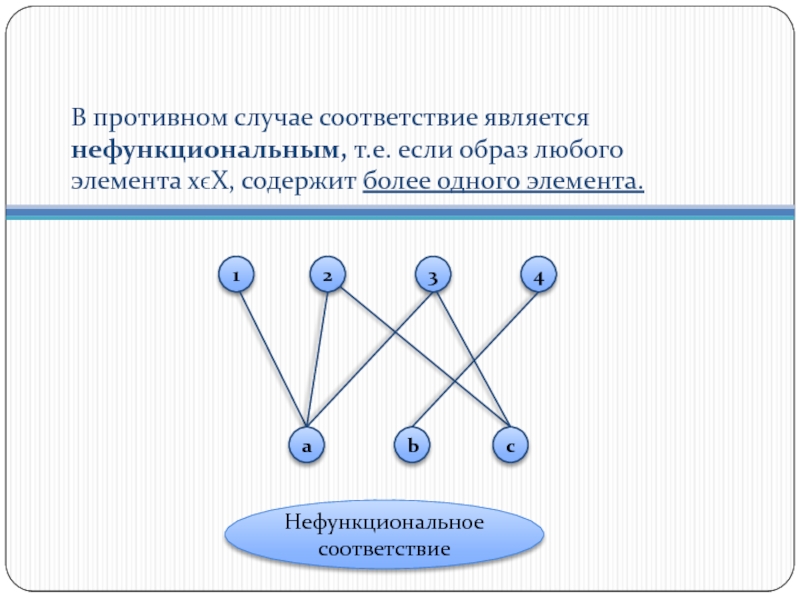
Слайд 9В противном случае соответствие является нефункциональным, т.е. если образ любого элемента
Нефункциональное соответствие
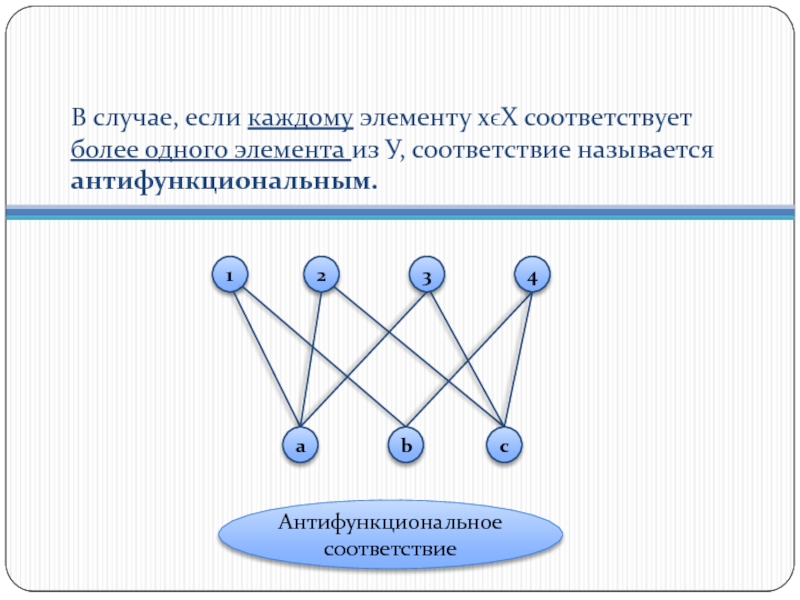
Слайд 10В случае, если каждому элементу хϵХ соответствует более одного элемента из
Антифункциональное соответствие
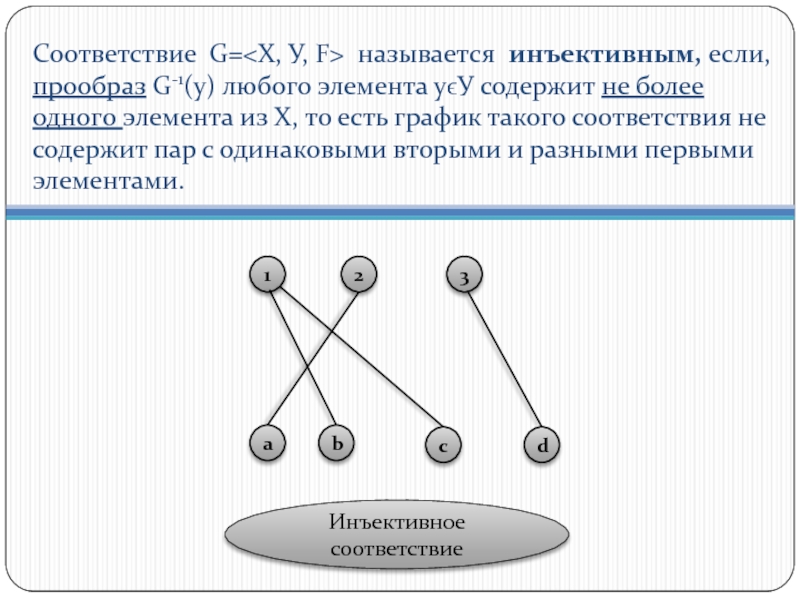
Слайд 11 Соответствие G= называется инъективным, если, прообраз G-1(у) любого элемента
Инъективное соответствие
Слайд 12 По аналогии можно определить понятие неинъективного соответствия. Соответствие G= называется
Неинъективное соответствие
Слайд 13 По аналогии можно определить понятие антиинъективного соответствия. Соответствие G= называется
Антиинъективное соответствие
Слайд 14Соответствие G= называется всюду определенным, если для каждого х , его
Всюду определенное соответствие
Слайд 15В противном случае соответствие является не всюду определенным.
Не всюду определенное
Слайд 16Соответствие G= называется сюръектиеным, если для любого уϵУ
Сюръективное соответствие
Слайд 18Соответствие называется биективным или взаимооднозначным, если оно функционально, инъективно, всюду определено
Биективное
взаимнооднозначное соответствие
Слайд 19Нефункциональное соответствие
Всюду определенное соответствие
Антиинъективное соответствие
Сюръективное соответствие
Определите свойства соответствий
Слайд 20Определите свойства соответствий
Антифункциональное соответствие
Всюду определенное соответствие
Неинъективное соответствие
Сюръективное соответствие
Слайд 21Постройте соответствие, обладающее следующими свойствами
Функциональное соответствие
Неинъективное соответствие
Несюръективное соответствие
Всюду определенное соответствие
Не всюду
Антифункциональное соответствие
Сюръективное соответствие
Неинъективное соответствие