- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
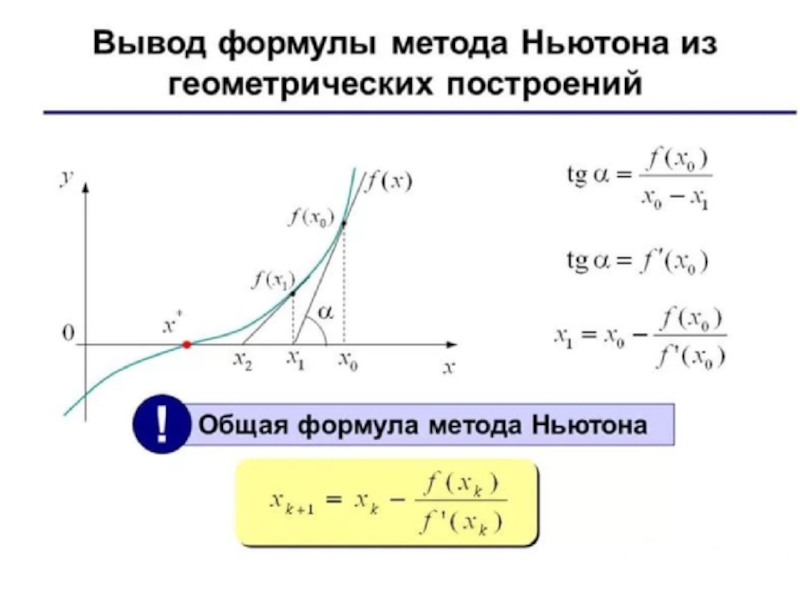
Суть метода Ньютона презентация
Содержание
- 1. Суть метода Ньютона
- 2. Суть метода Ньютона
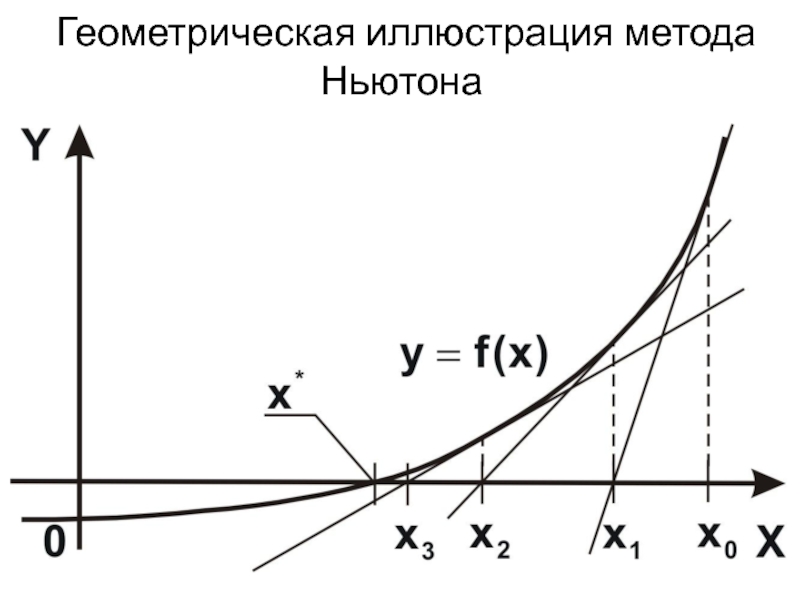
- 3. Геометрическая иллюстрация метода Ньютона
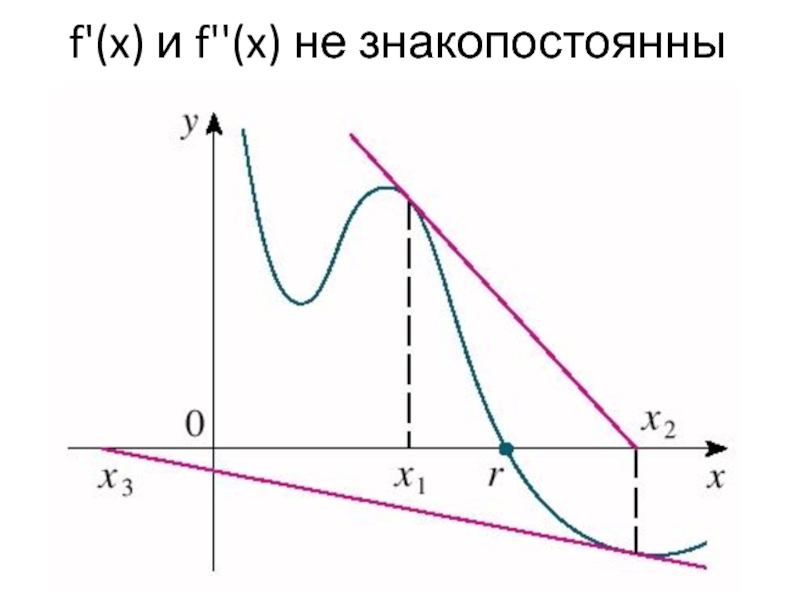
- 5. f'(x) и f''(x) не знакопостоянны
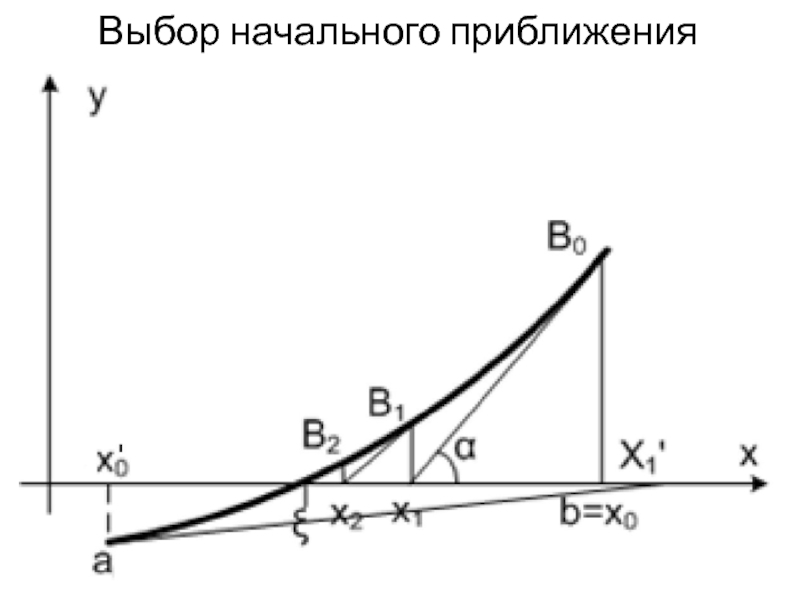
- 6. Выбор начального приближения
- 7. Теорема о сходимости метода Ньютона
- 8. Проверка условий сходимости метода Ньютона
- 9. Последовательность приближений по методу Ньютона
- 10. Оценка погрешности приближения для метода Ньютона
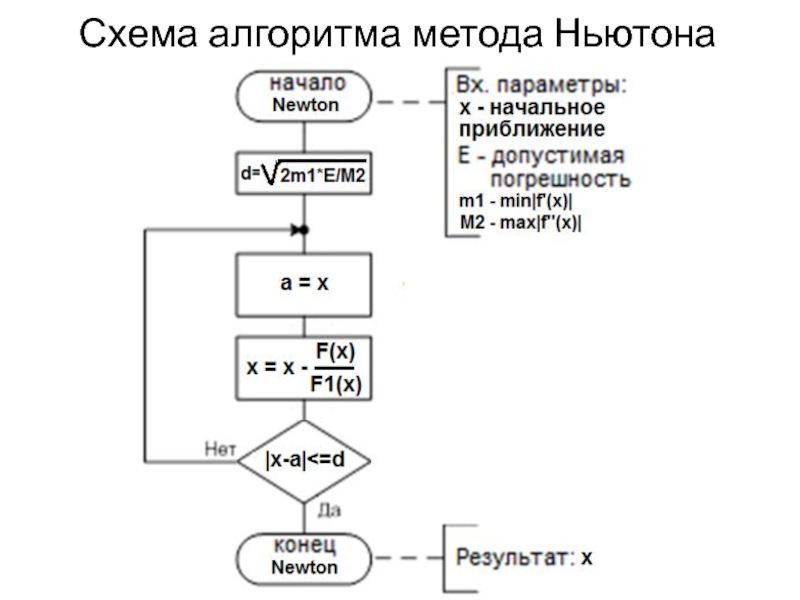
- 11. Схема алгоритма метода Ньютона
- 12. Геометрическая иллюстрация метода хорд. Случай f'(x) >
- 13. Геометрическая иллюстрация метода хорд. Случай f'(x) >
- 14. Выбор неподвижной точки и начального приближения Из
- 15. Последовательность приближений по методу хорд
- 16. Оценка погрешности приближения для метода хорд
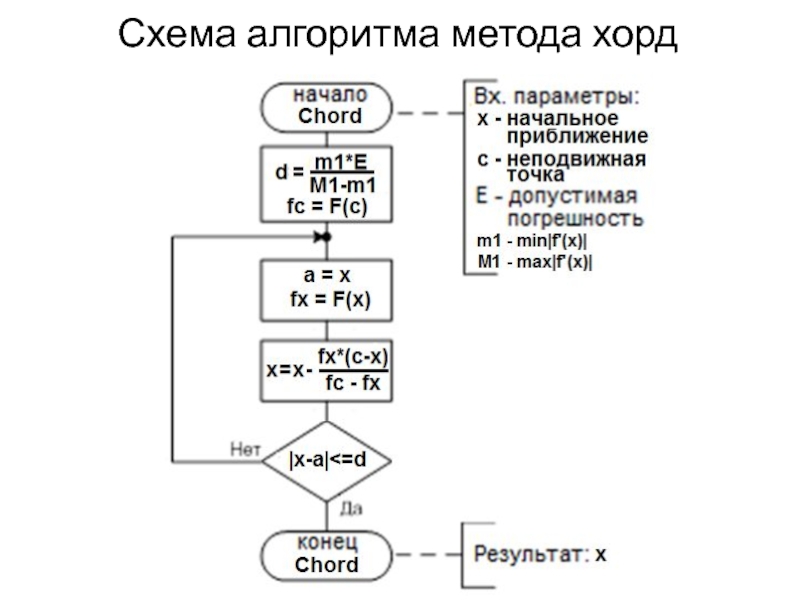
- 17. Схема алгоритма метода хорд
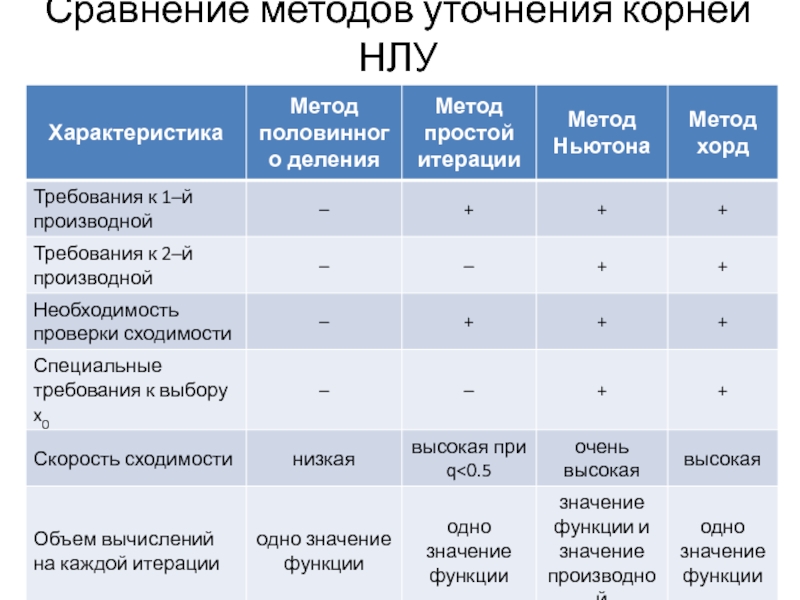
- 18. Сравнение методов уточнения корней НЛУ
Слайд 1Лекция 7
Метод Ньютона (метод касательных)
Метод хорд
Сравнение методов уточнения корней нелинейных уравнений
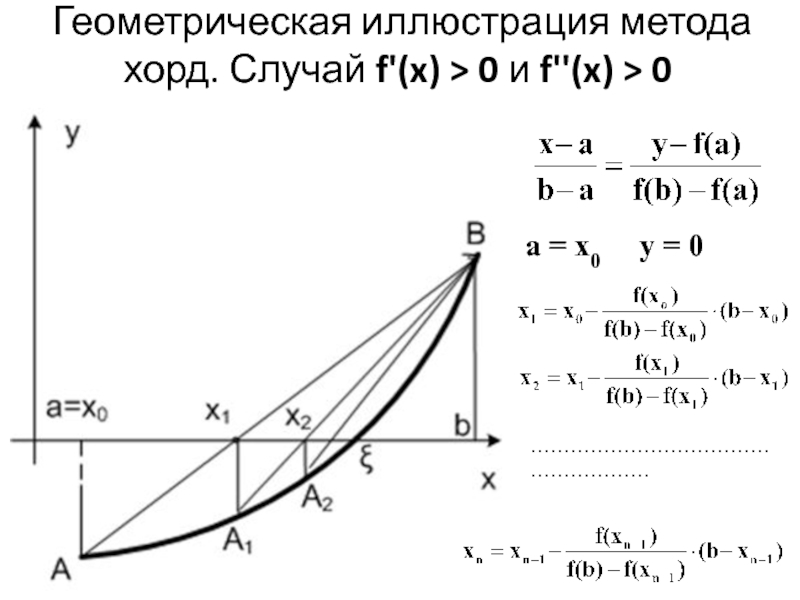
Слайд 12Геометрическая иллюстрация метода хорд. Случай f'(x) > 0 и f''(x) >
0
a = x0 y = 0
………………………………………………
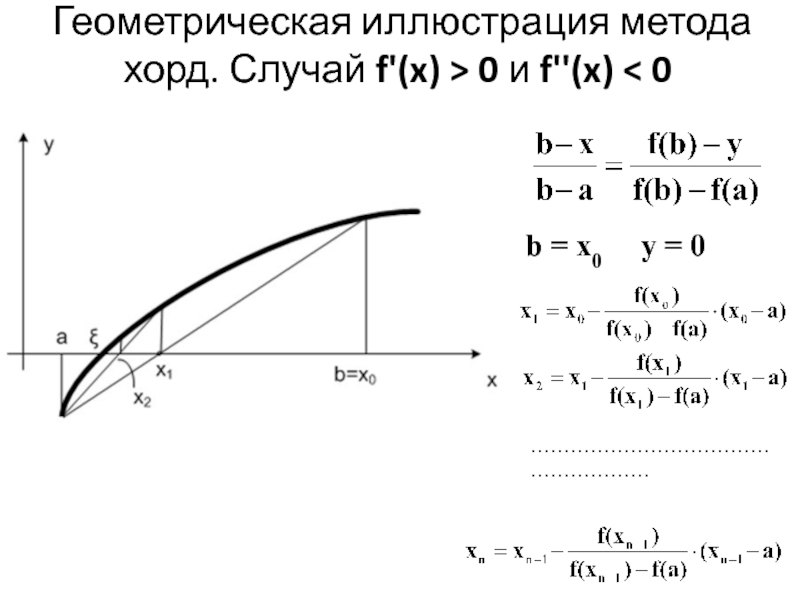
Слайд 13Геометрическая иллюстрация метода хорд. Случай f'(x) > 0 и f''(x)
0
b = x0 y = 0
………………………………………………
Слайд 14Выбор неподвижной точки и начального приближения
Из рассмотренных построений видно, что один
из концов отрезка отделения корня в процессе итераций остается неподвижным, а противоположный конец вначале принимается за начальное приближение, а затем постепенно смещается в сторону корня, образуя последовательность приближений. Общее правило таково:
за неподвижную точку в методе хорд выбирается тот конец отрезка [a;b], на котором знак функции совпадает со знаком второй производной: f(x)∙f’’(x)>0; в качестве начального приближения выбирается противоположный конец отрезка.
за неподвижную точку в методе хорд выбирается тот конец отрезка [a;b], на котором знак функции совпадает со знаком второй производной: f(x)∙f’’(x)>0; в качестве начального приближения выбирается противоположный конец отрезка.