ЛА-УП-Л5 презентация

Содержание

1. ЛА-УП-Л5
2. План лекции Понятие n-мерного вектора Действия над
3. Пространство n-мерных векторов. Множество столбцов вещественных чисел высоты n:
4. Действия над n-мерными векторами Суммой двух векторов X
5. Действия над n-мерными векторами Произведением числа λ и вектора X
6. n-мерное координатное пространство Множество V n-мерных векторов
7. Свойства операций над векторами X+Y=Y+X (X+Y)+Z=X+(Y+Z) X+0=X
8. Скалярное произведение Скалярным произведением векторов называется число
9. Свойства скалярного произведения (X,Y)=(Y,X) (λX,Y)= λ(X,Y) (X+Y,Z)=(X,Z)+(Y,Z)
10. Длина вектора Длиной (нормой) вектора называется число
11. Угол между векторами Угол между векторами
12. Линейная комбинация векторов. Определение Линейной комбинацией
13. Линейная зависимость и линейная независимость векторов
14. Показать, что система столбцов линейно зависима.
15. Критерии линейной зависимости Система векторов X1,…,Xm линейно зависима

План лекции Понятие n-мерного вектора Действия над векторами и их свойства Скалярное произведение векторов Длина вектора. Угол между векторами. Линейная комбинация векторов. Линейная независимость.

Слайд 1Линейная алгебра
Лекция 5
Векторы

Слайд 2План лекции
Понятие n-мерного вектора
Действия над векторами и их свойства
Скалярное произведение векторов
Длина

вектора.
Угол между векторами.
Линейная комбинация векторов.
Линейная независимость.

Слайд 3

Пространство n-мерных векторов.
Множество столбцов вещественных чисел высоты n:

Слайд 4Действия над n-мерными векторами
Суммой двух векторов X и Y называется вектор, координаты

которого равны сумме соответствующих координат исходных векторов, то есть:

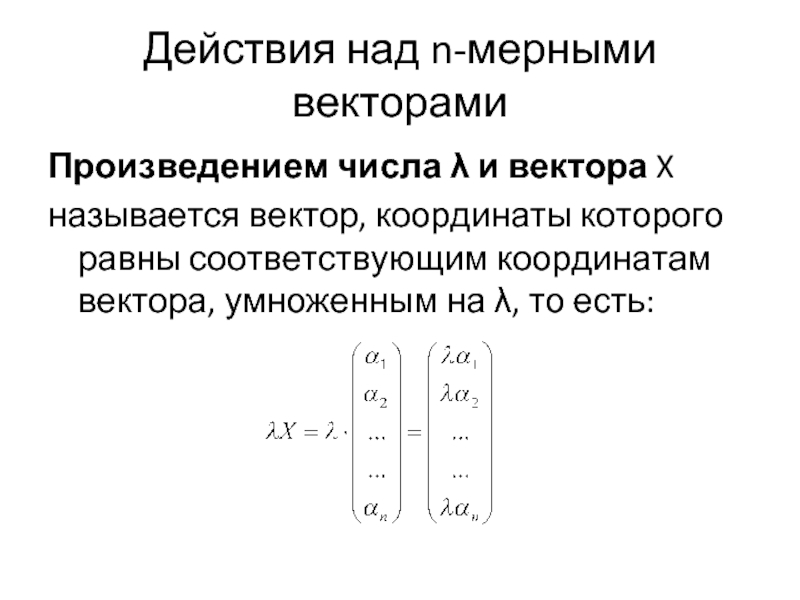
Слайд 5Действия над n-мерными векторами
Произведением числа λ и вектора X
называется вектор, координаты которого равны соответствующим

координатам вектора, умноженным на λ, то есть:

Слайд 6n-мерное координатное пространство
Множество V n-мерных векторов вместе с введенными выше операциями

сложения векторов и умножения вектора на число называется n-мерным координатным пространством. Обозначение: Rn

Слайд 7Свойства операций над векторами
X+Y=Y+X
(X+Y)+Z=X+(Y+Z)
X+0=X
X+(-X)=0
(λ+μ)X= λX+μX
λ(X+Y)= λX+ λY
(λ μ)X= λ (μX)
1 ∙X=X

Слайд 8Скалярное произведение
Скалярным произведением векторов

называется число

Слайд 9Свойства скалярного произведения
(X,Y)=(Y,X)
(λX,Y)= λ(X,Y)
(X+Y,Z)=(X,Z)+(Y,Z)
(X,X)≥0, причем (X,X)=0 тогда и только тогда, когда

X=0.

Слайд 10Длина вектора
Длиной (нормой) вектора

называется число

Слайд 11Угол между векторами
Угол между векторами

Для ортогональных векторов (X,Y)=0.

Слайд 12Линейная комбинация векторов. Определение

Линейной комбинацией векторов

называют вектор

при некоторых коэффициентах

Слайд 13Линейная зависимость и линейная независимость векторов
Определение
Совокупность векторов

называется линейно зависимой (ЛЗС), если найдутся числа , не равные нулю одновременно, такие, что выполняется равенство:

В противном случае совокупность
называется линейно независимой (ЛНС).

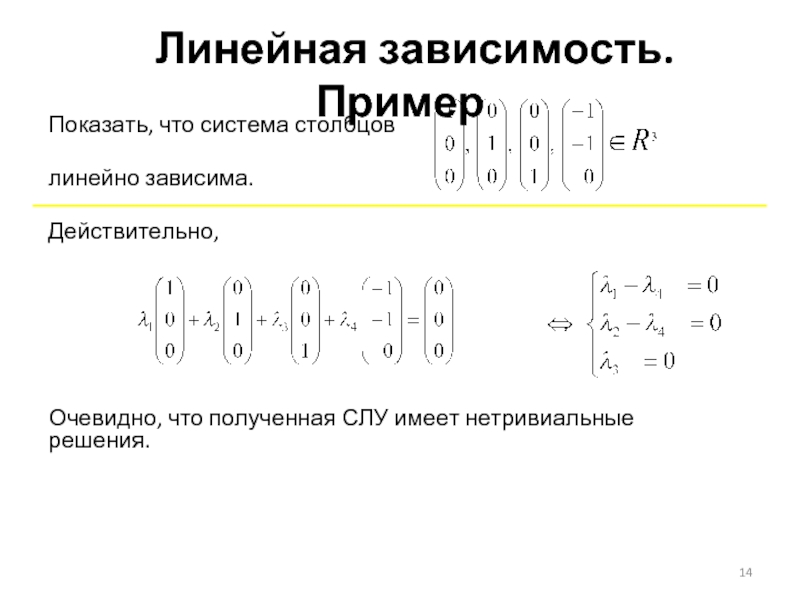
Слайд 14Показать, что система столбцов

линейно зависима.

Действительно,

Очевидно, что полученная СЛУ имеет нетривиальные решения.

Линейная зависимость. Пример

Слайд 15Критерии линейной зависимости
Система векторов X1,…,Xm линейно зависима тогда и только тогда, когда

хотя бы один вектор системы линейно выражается через остальные.
Cистема n-мерных векторов X1,…,Xn линейно зависима тогда и только тогда, когда определитель, строками (столбцами) которого являются компоненты векторов системы равен нулю.
Следствие:
Если система содержит нулевой элемент или линейно зависимую подсистему, то она линейно зависима.

Скачать презентацию

ЛА-УП-Л5 презентация

Содержание

Слайд 1Линейная алгебра
Лекция 5
Векторы

Слайд 2План лекции
Понятие n-мерного вектора
Действия над векторами и их свойства
Скалярное произведение векторов
Длина

Слайд 3

Пространство n-мерных векторов.
Множество столбцов вещественных чисел высоты n:

Слайд 4Действия над n-мерными векторами
Суммой двух векторов X и Y называется вектор, координаты

Слайд 5Действия над n-мерными векторами
Произведением числа λ и вектора X
называется вектор, координаты которого равны соответствующим

Слайд 6n-мерное координатное пространство
Множество V n-мерных векторов вместе с введенными выше операциями

Слайд 7Свойства операций над векторами
X+Y=Y+X
(X+Y)+Z=X+(Y+Z)
X+0=X
X+(-X)=0
(λ+μ)X= λX+μX
λ(X+Y)= λX+ λY
(λ μ)X= λ (μX)
1 ∙X=X

Слайд 8Скалярное произведение
Скалярным произведением векторов

называется число

Слайд 9Свойства скалярного произведения
(X,Y)=(Y,X)
(λX,Y)= λ(X,Y)
(X+Y,Z)=(X,Z)+(Y,Z)
(X,X)≥0, причем (X,X)=0 тогда и только тогда, когда

Слайд 10Длина вектора
Длиной (нормой) вектора

называется число

Слайд 11Угол между векторами
Угол между векторами

Для ортогональных векторов (X,Y)=0.

Слайд 12Линейная комбинация векторов. Определение

Линейной комбинацией векторов

Слайд 13Линейная зависимость и линейная независимость векторов
Определение
Совокупность векторов

Слайд 14Показать, что система столбцов

линейно зависима.

Действительно,

Очевидно, что полученная СЛУ имеет нетривиальные решения.

Слайд 15Критерии линейной зависимости
Система векторов X1,…,Xm линейно зависима тогда и только тогда, когда

Обратная связь

Что такое ThePresentation.ru?

ЛА-УП-Л5 презентация

Содержание

Слайд 1Линейная алгебраЛекция 5Векторы

Слайд 2План лекцииПонятие n-мерного вектораДействия над векторами и их свойстваСкалярное произведение векторовДлина

Слайд 3Пространство n-мерных векторов.Множество столбцов вещественных чисел высоты n:

Слайд 4Действия над n-мерными векторамиСуммой двух векторов X и Y называется вектор, координаты

Слайд 5Действия над n-мерными векторамиПроизведением числа λ и вектора X называется вектор, координаты которого равны соответствующим

Слайд 6n-мерное координатное пространствоМножество V n-мерных векторов вместе с введенными выше операциями

Слайд 7Свойства операций над векторамиX+Y=Y+X(X+Y)+Z=X+(Y+Z)X+0=XX+(-X)=0(λ+μ)X= λX+μXλ(X+Y)= λX+ λY(λ μ)X= λ (μX)1 ∙X=X

Слайд 8Скалярное произведениеСкалярным произведением векторов называется число

Слайд 9Свойства скалярного произведения(X,Y)=(Y,X)(λX,Y)= λ(X,Y)(X+Y,Z)=(X,Z)+(Y,Z)(X,X)≥0, причем (X,X)=0 тогда и только тогда, когда

Слайд 10Длина вектораДлиной (нормой) вектора называется число

Слайд 11Угол между векторамиУгол между векторамиДля ортогональных векторов (X,Y)=0.

Слайд 12Линейная комбинация векторов. ОпределениеЛинейной комбинацией векторов

Слайд 13Линейная зависимость и линейная независимость векторовОпределениеСовокупность векторов

Слайд 14Показать, что система столбцовлинейно зависима.Действительно,Очевидно, что полученная СЛУ имеет нетривиальные решения.

Слайд 15Критерии линейной зависимостиСистема векторов X1,…,Xm линейно зависима тогда и только тогда, когда

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1Линейная алгебра
Лекция 5
Векторы

Слайд 2План лекции
Понятие n-мерного вектора
Действия над векторами и их свойства
Скалярное произведение векторов
Длина

Слайд 3

Пространство n-мерных векторов.
Множество столбцов вещественных чисел высоты n:

Слайд 4Действия над n-мерными векторами
Суммой двух векторов X и Y называется вектор, координаты

Слайд 5Действия над n-мерными векторами
Произведением числа λ и вектора X
называется вектор, координаты которого равны соответствующим

Слайд 6n-мерное координатное пространство
Множество V n-мерных векторов вместе с введенными выше операциями

Слайд 7Свойства операций над векторами
X+Y=Y+X
(X+Y)+Z=X+(Y+Z)
X+0=X
X+(-X)=0
(λ+μ)X= λX+μX
λ(X+Y)= λX+ λY
(λ μ)X= λ (μX)
1 ∙X=X

Слайд 8Скалярное произведение
Скалярным произведением векторов

называется число

Слайд 9Свойства скалярного произведения
(X,Y)=(Y,X)
(λX,Y)= λ(X,Y)
(X+Y,Z)=(X,Z)+(Y,Z)
(X,X)≥0, причем (X,X)=0 тогда и только тогда, когда

Слайд 10Длина вектора
Длиной (нормой) вектора

называется число

Слайд 11Угол между векторами
Угол между векторами

Для ортогональных векторов (X,Y)=0.

Слайд 12Линейная комбинация векторов. Определение

Линейной комбинацией векторов

Слайд 13Линейная зависимость и линейная независимость векторов
Определение
Совокупность векторов

Слайд 14Показать, что система столбцов

линейно зависима.

Действительно,

Очевидно, что полученная СЛУ имеет нетривиальные решения.

Слайд 15Критерии линейной зависимости
Система векторов X1,…,Xm линейно зависима тогда и только тогда, когда