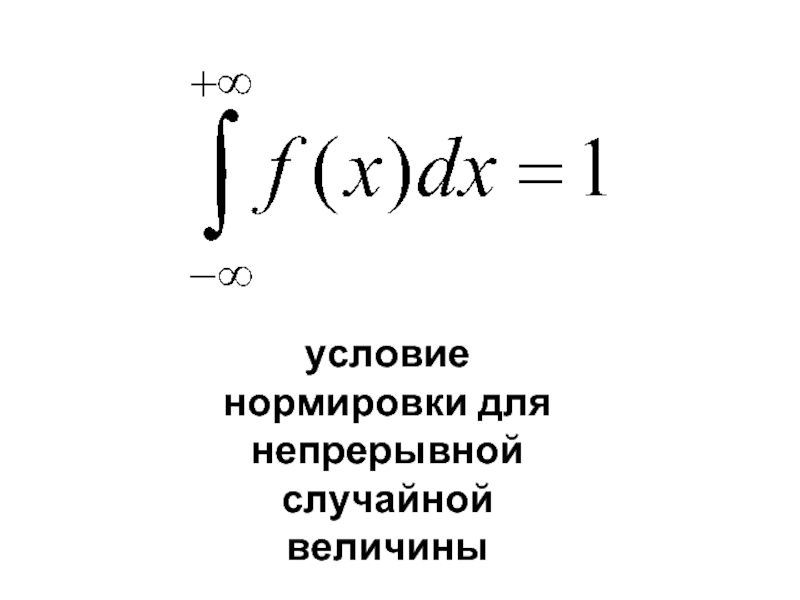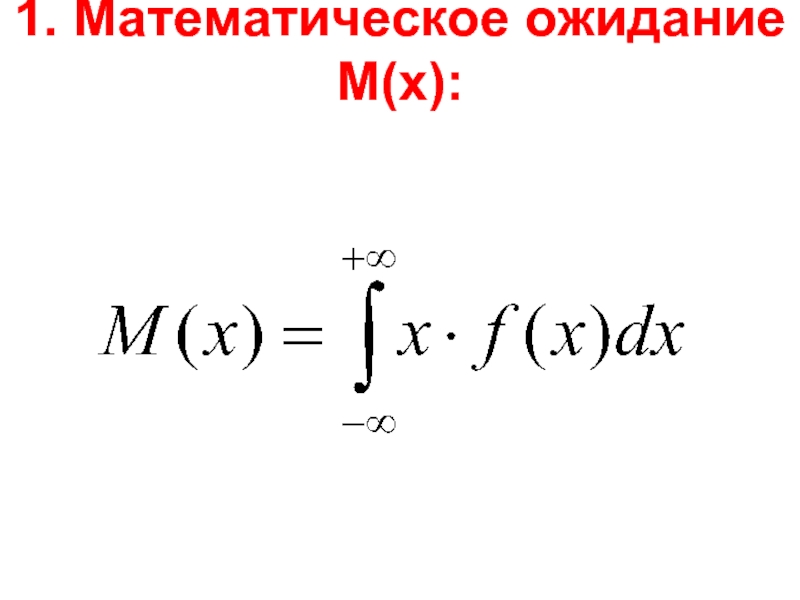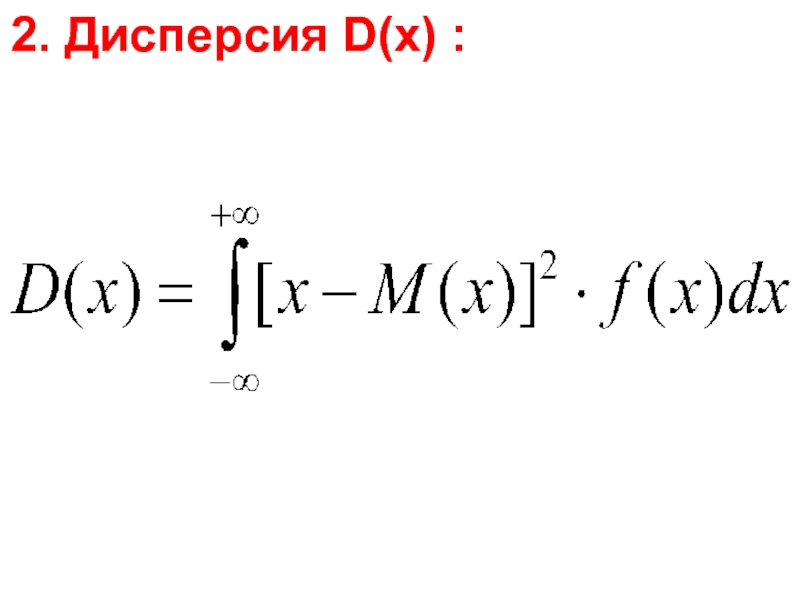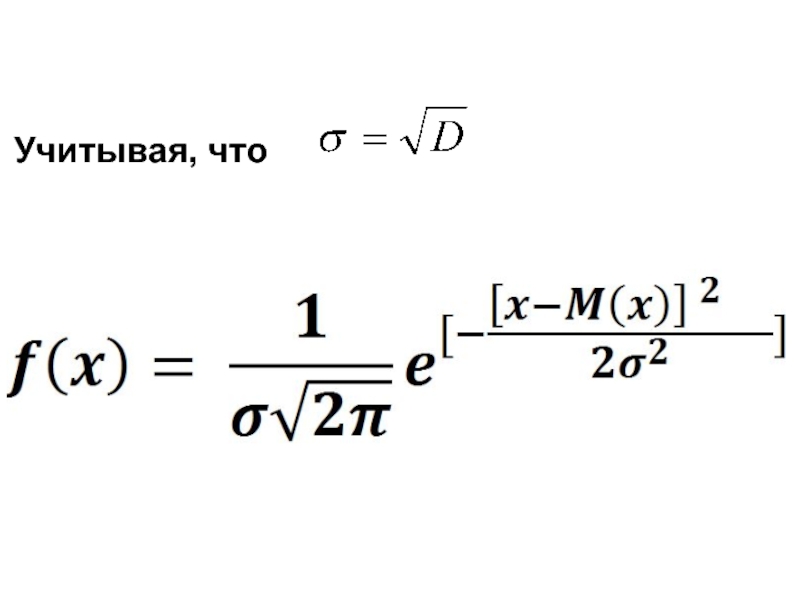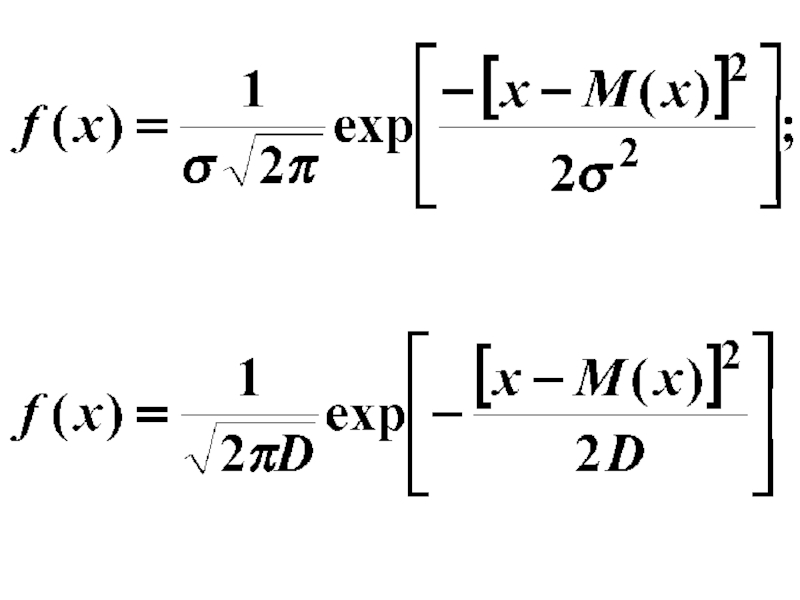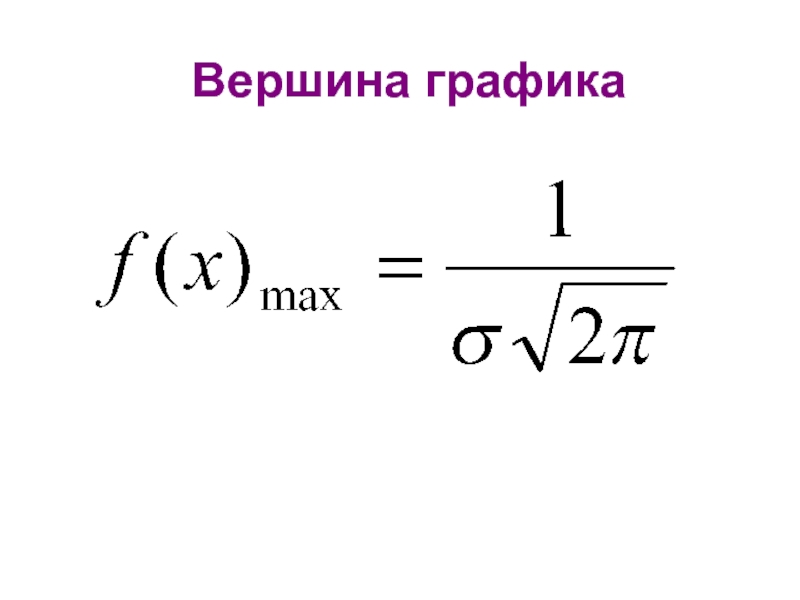- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические методы обработки медико-биологических данных. Нормальный закон распределения презентация
Содержание
- 1. Статистические методы обработки медико-биологических данных. Нормальный закон распределения
- 2. Тема: Статистические методы обработки медико-биологических данных Нормальный
- 3. В медицине необходимо вести учет, анализ и
- 4. Закономерности массовых случайных событий -
- 5. Типичная задача математической статистики - это
- 6. Случайной величиной называется переменная
- 7. Дискретной называется случайная величина, которая может принимать
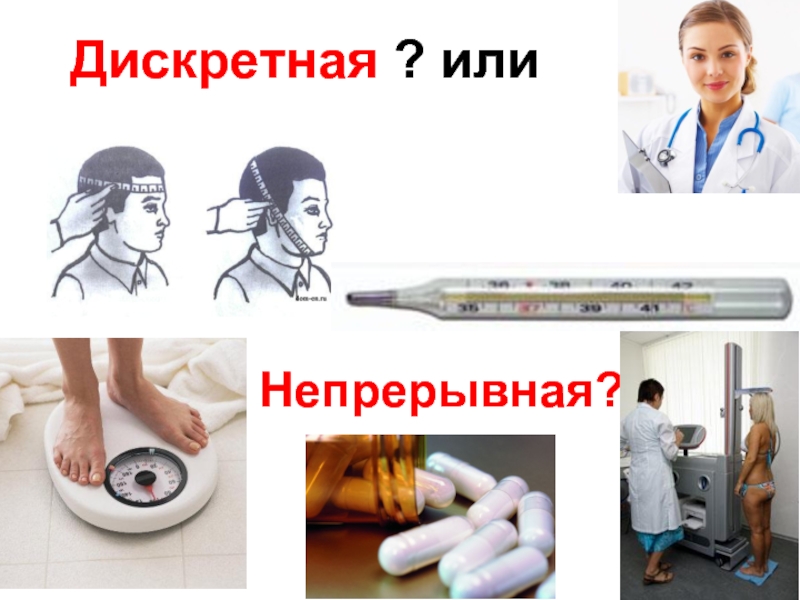
- 9. Непрерывная? Дискретная ? или
- 10. Статистический ряд – результаты измерений для статистического
- 11. Распределение дискретной случайной величины.
- 12. Совокупность X и Р называется распределением дискретной случайной величины.
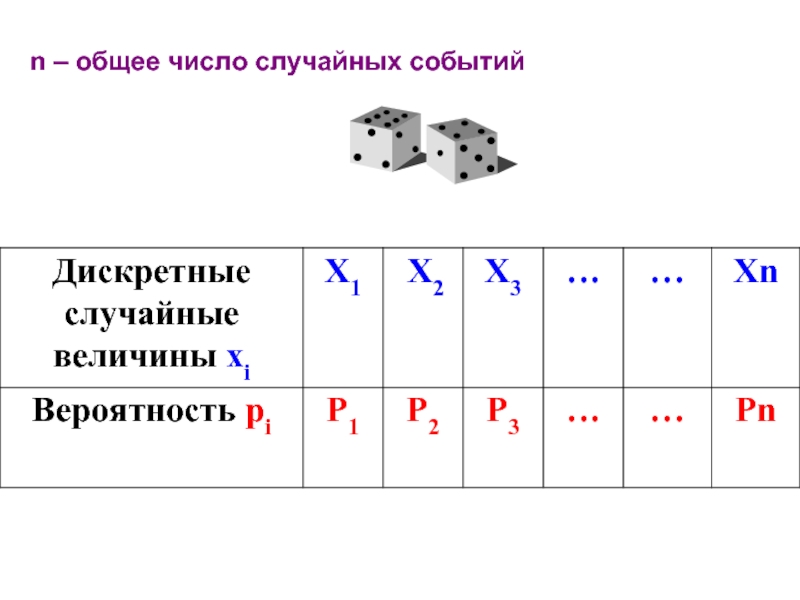
- 13. n – общее число случайных событий
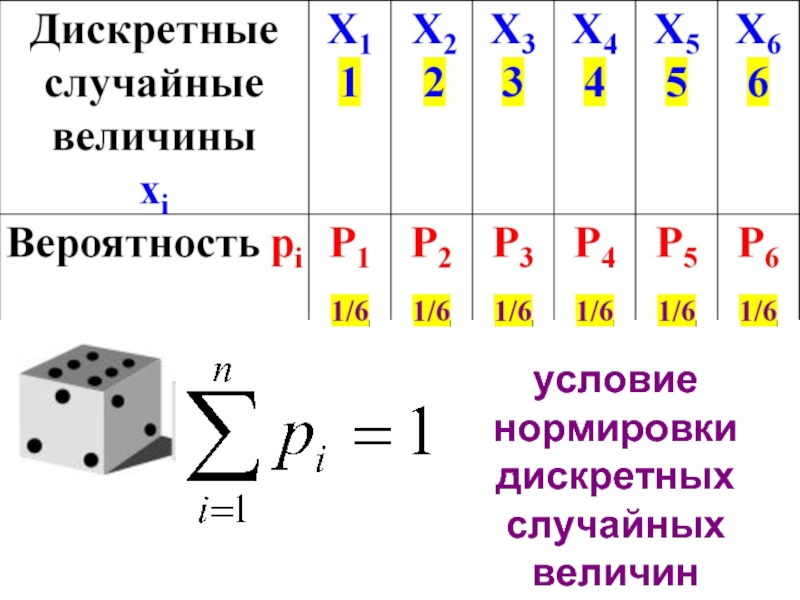
- 15. Различные распределения 1. Биномиальное распределение
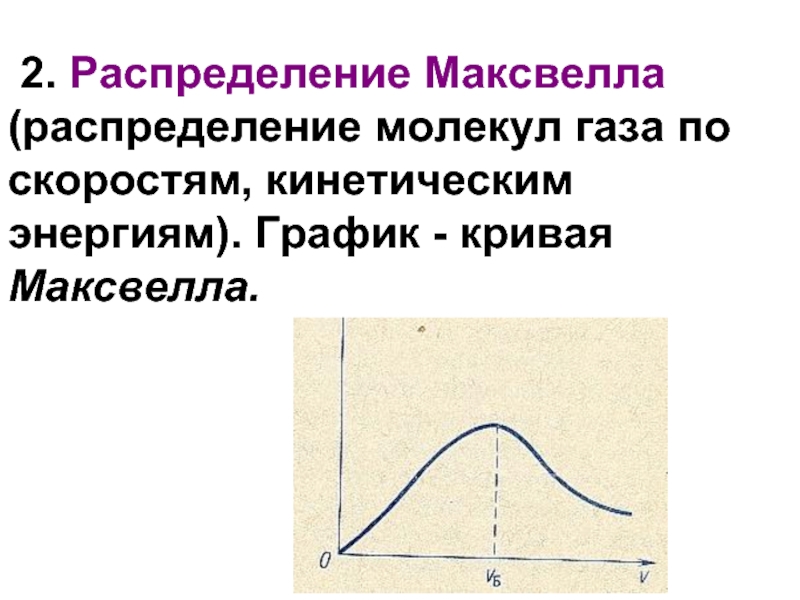
- 16. 2. Распределение Максвелла (распределение молекул
- 17. 3. Распределение Больцмана (распределение частиц по потенциальным
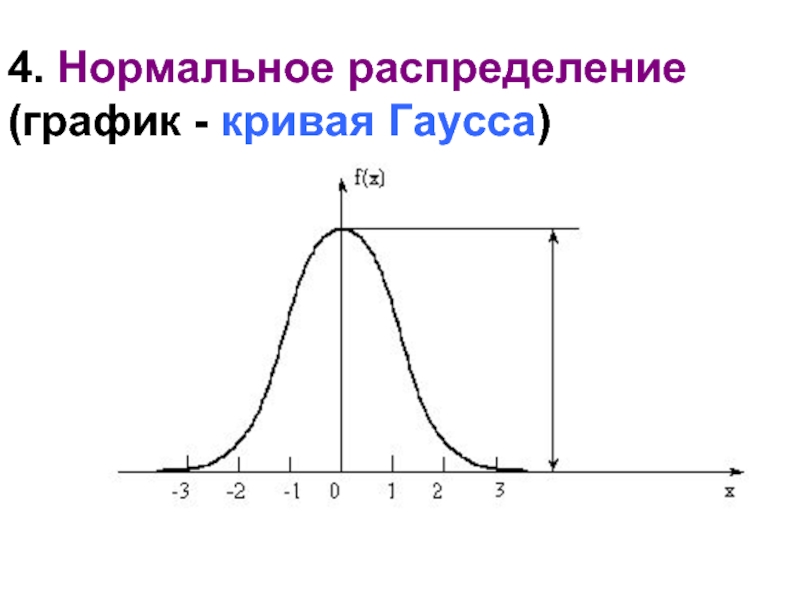
- 18. 4. Нормальное распределение (график - кривая Гаусса)
- 19. 5. Распределение Пуассона и др. ...
- 20. Нормальный закон распределения имеет важное практическое значение
- 21. Числовые характеристики дискретных случайных величин.
- 22. 1.Математическое ожидание случайной величины есть сумма произведений
- 23. 2. Среднее арифметическое значение n – число измерений.
- 24. Если n велико ,
- 25. 3. Дисперсия случайной величины – это
- 26. Дисперсия характеризует рассеяние случайных величин относительно математического
- 27. Размерность дисперсии - квадрат размерности случайной величины,
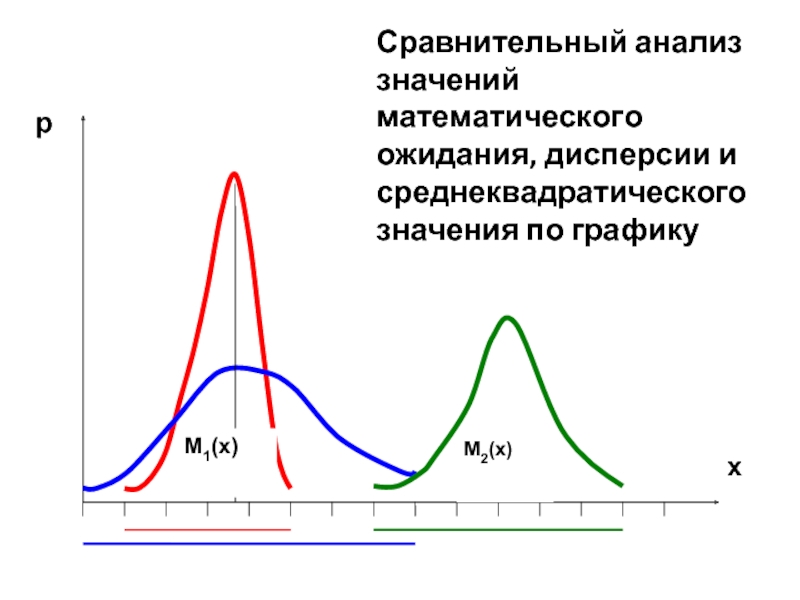
- 28. Сравнительный анализ значений математического ожидания, дисперсии и среднеквадратического значения по графику
- 29. Числовые характеристики непрерывных случайных величин.
- 30. dP - вероятность того, что непрерывная случайная
- 31. функция распределения вероятности показывает, как изменяется вероятность,
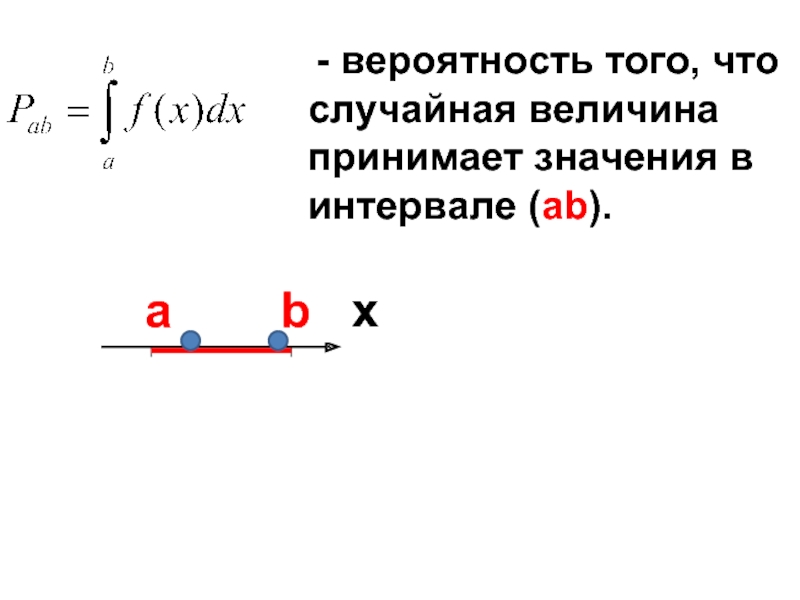
- 32. - вероятность того, что случайная
- 33. -∞
- 34. - условие нормировки для непрерывной случайной величины
- 35. 1. Математическое ожидание М(х):
- 36. 2. Дисперсия D(x) :
- 37. 3. Среднеквадратическое отклонение, которое имеет размерность случайной величины.
- 38. Нормальный закон распределения: ехр - экспонента; е±x= ехр(±х);
- 39. График нормального закона - кривая Гаусса.
- 40. Учитывая, что
- 42. ветви – экспоненты (возрастающая и убывающая)
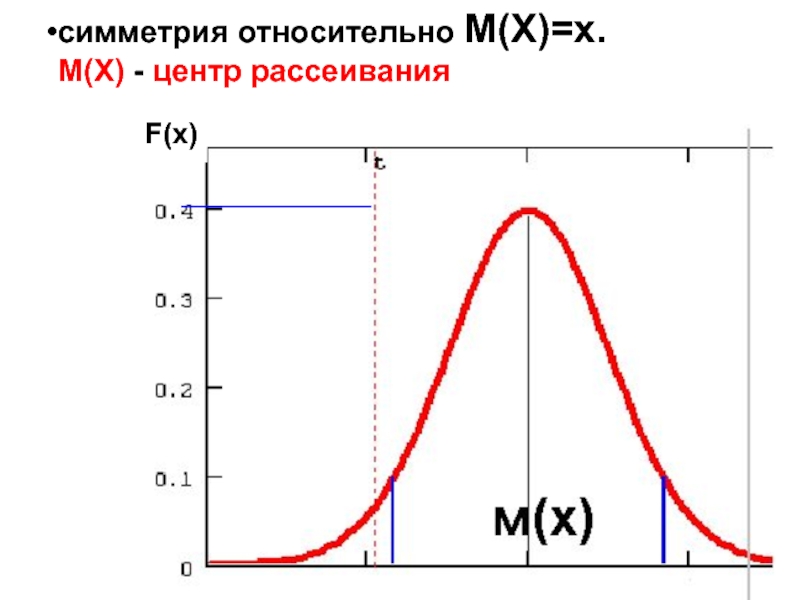
- 43. F(x) симметрия относительно М(Х)=х. М(Х) - центр рассеивания х
- 44. по данной формуле определяем координаты вершины кривой Гаусса, когда х = М(х).
- 45. Вершина графика
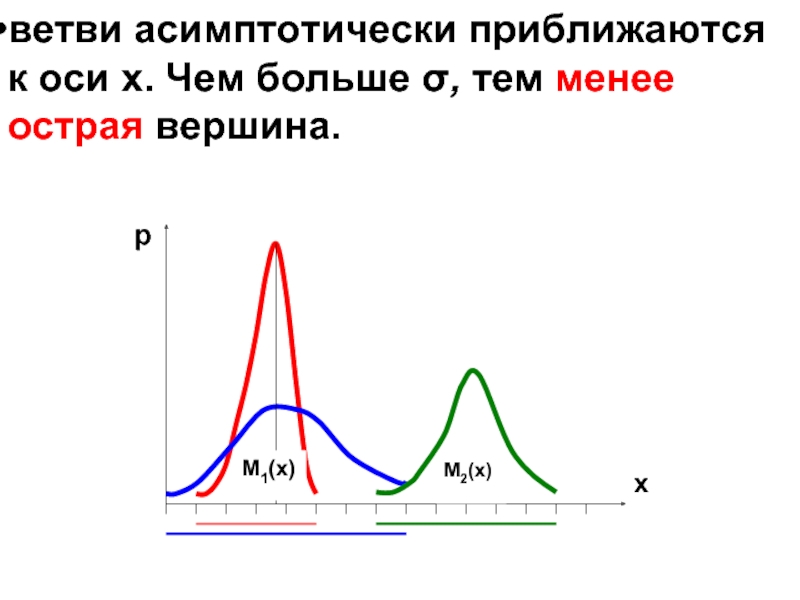
- 46. ветви асимптотически приближаются к оси х. Чем больше σ, тем менее острая вершина.
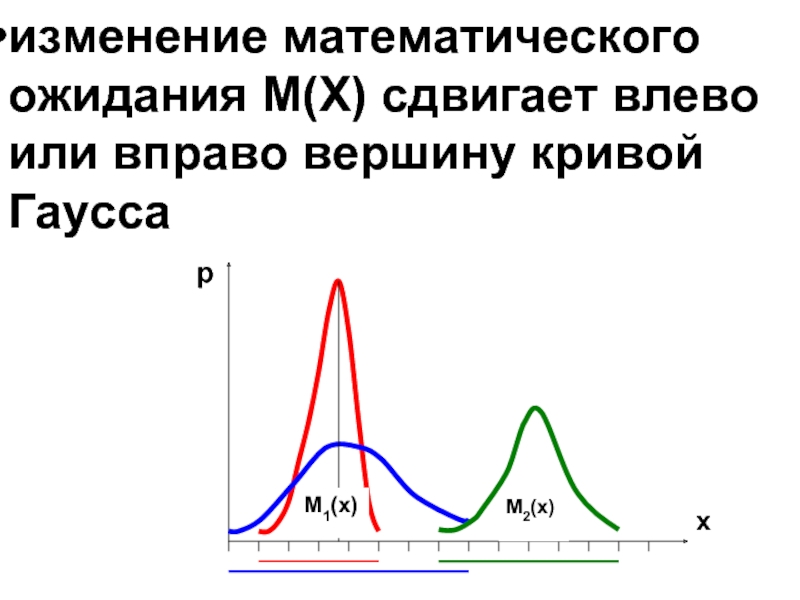
- 47. изменение математического ожидания М(Х) сдвигает влево или вправо вершину кривой Гаусса
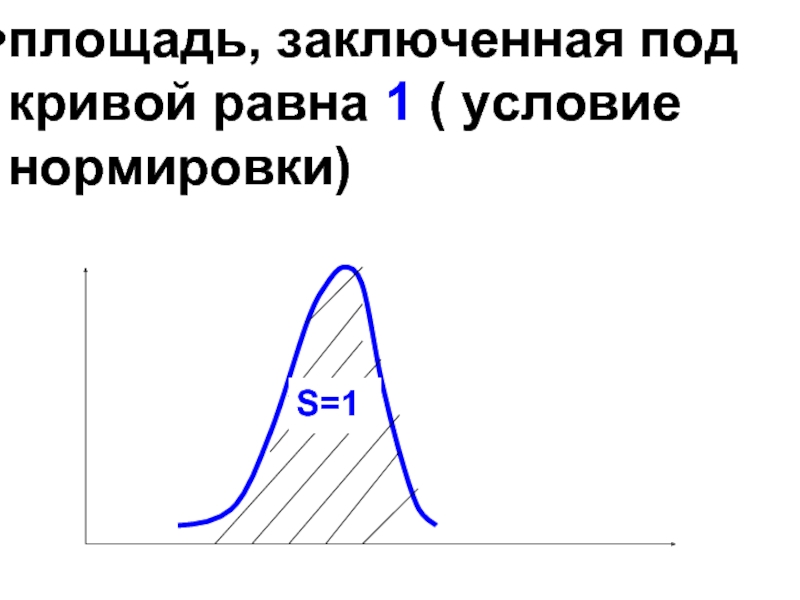
- 48. площадь, заключенная под кривой равна 1 ( условие нормировки)
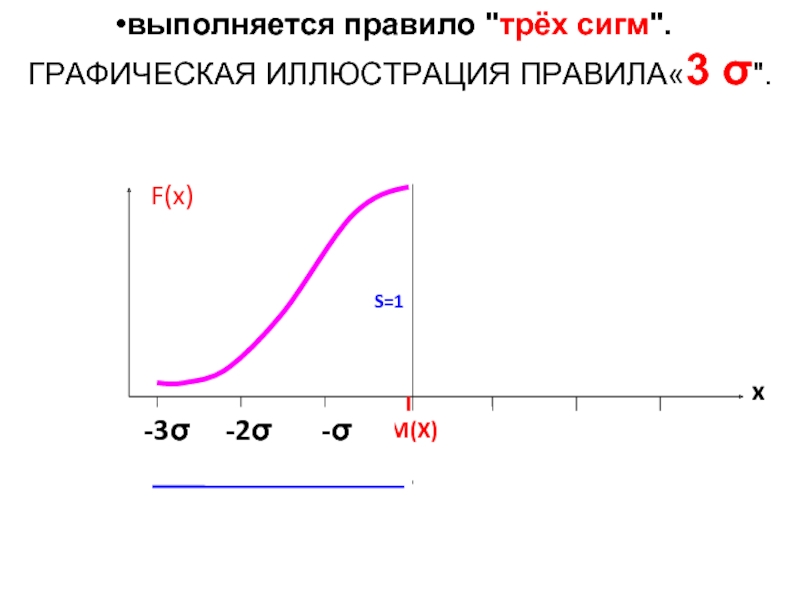
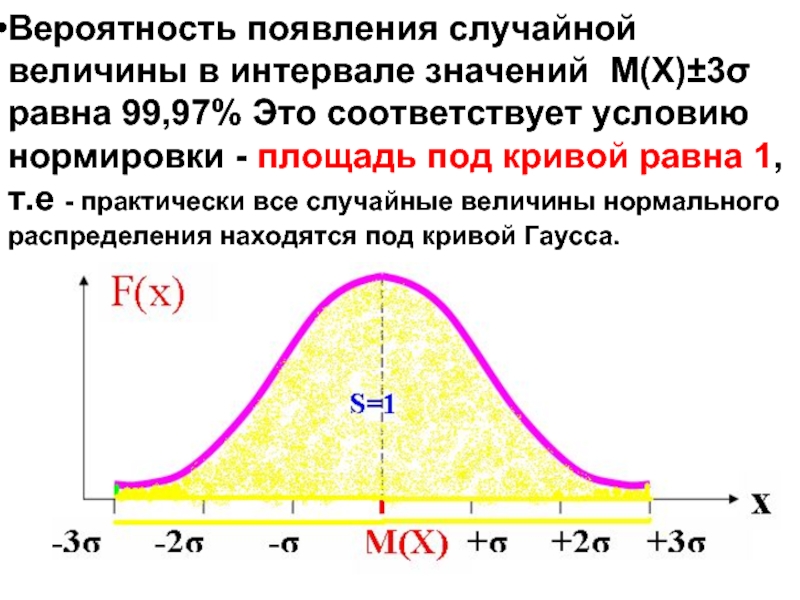
- 49. выполняется правило "трёх сигм". ГРАФИЧЕСКАЯ ИЛЛЮСТРАЦИЯ ПРАВИЛА«3 σ".
- 50. Вероятность появления случайной величины в интервале значений
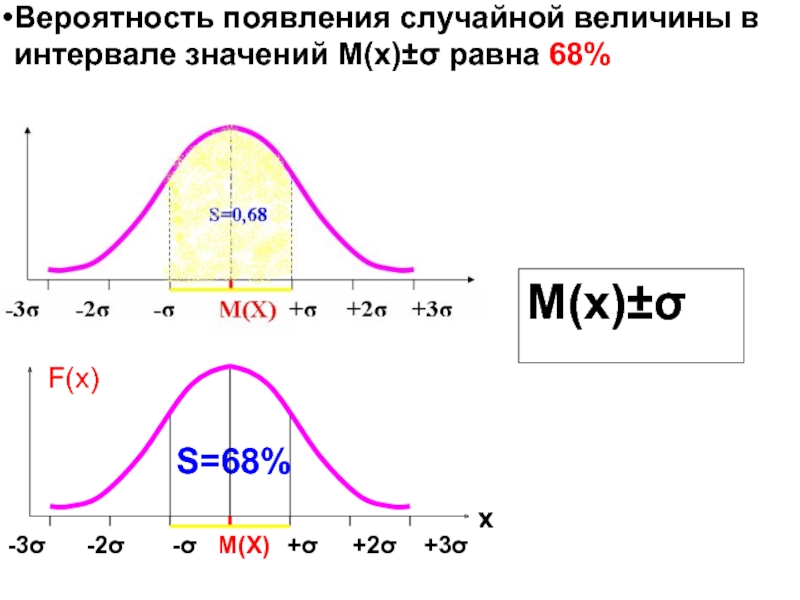
- 51. М(х)±σ Вероятность появления случайной величины в интервале значений М(х)±σ равна 68%
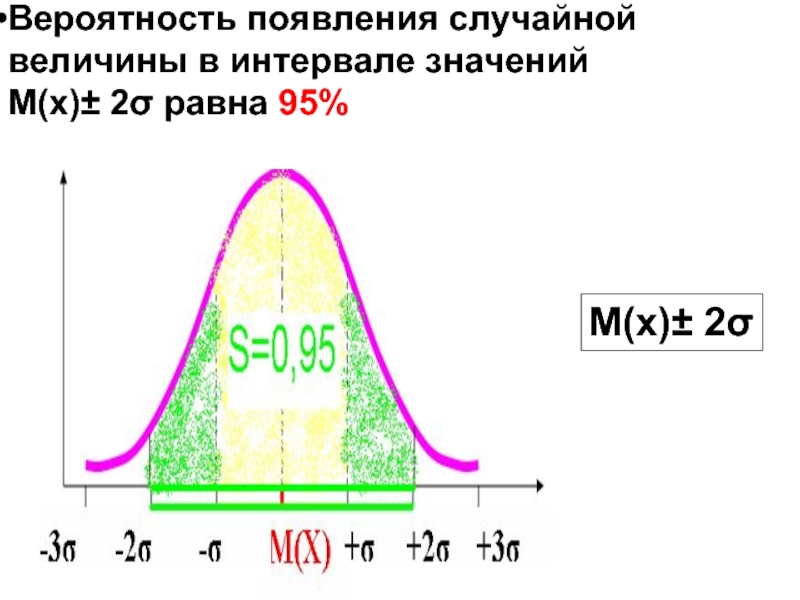
- 52. М(х)± 2σ Вероятность появления случайной величины в интервале значений М(х)± 2σ равна 95%
- 53. Для нормального закона распределения характерен симметричный вид
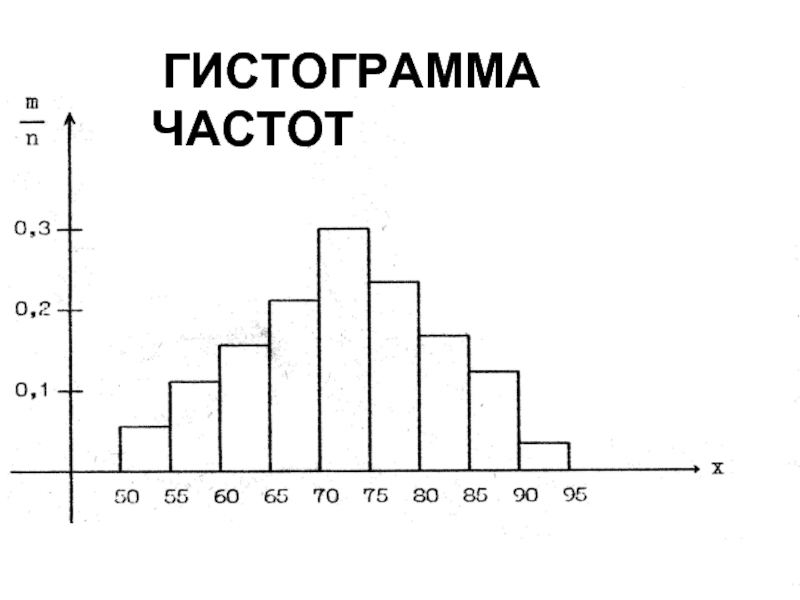
- 54. ГИСТОГРАММА ЧАСТОТ
- 55. m/n 0,4
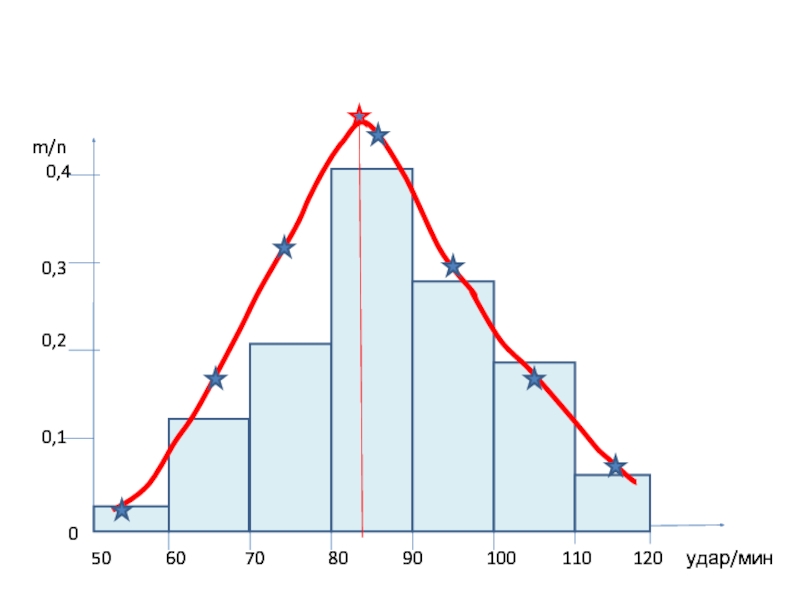
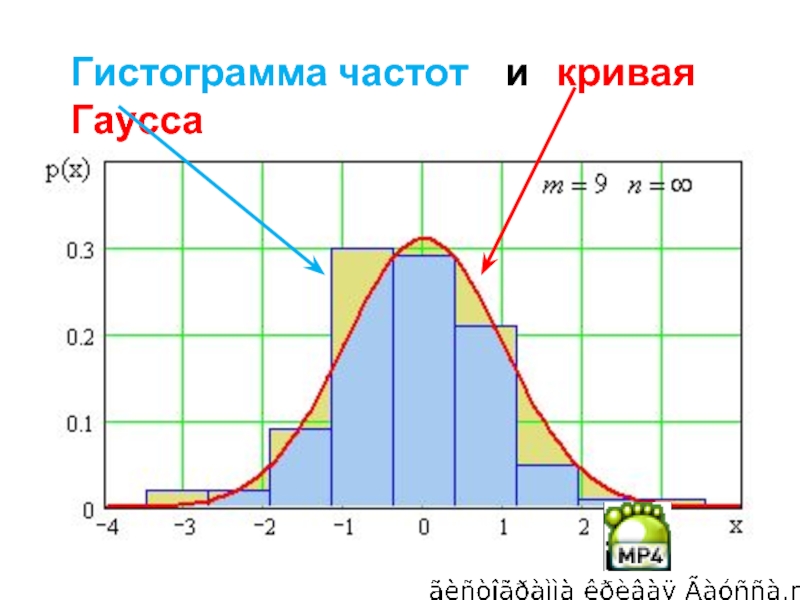
- 56. Гистограмма частот и кривая Гаусса
Тема: Статистические методы обработки медико-биологических данных Нормальный закон распределения. План лекции: Понятие случайных дискретных и непрерывных величин. Распределения и характеристики случайных величин. Нормальный
Слайд 2Тема: Статистические методы обработки медико-биологических данных
Нормальный закон распределения.
План лекции:
Понятие случайных дискретных и непрерывных величин.
Распределения и характеристики случайных величин.
Нормальный закон распределения. Кривая Гаусса и ее особенности. Правило «трёх сигм».
Понятие случайных дискретных и непрерывных величин.
Распределения и характеристики случайных величин.
Нормальный закон распределения. Кривая Гаусса и ее особенности. Правило «трёх сигм».
Слайд 3В медицине необходимо вести учет, анализ и прогноз различных массовых явлений.
В целом, массовым явлениям присущи свои особые закономерности. К доктору обращаются пациенты с различными заболеваниями. Болезнь конкретного человека - случайное событие у врача. Но случайные события предсказуемы, например, в период эпидемии гриппа наиболее часто встречаются заболевания гриппом.
Слайд 4
Закономерности массовых случайных событий - статистических данных, отражающих эти события, -
изучаются с помощью математической статистики.
Слайд 5
Типичная задача математической статистики - это приближенная оценка неизвестной вероятности случайного
события по результатам наблюдений, экспериментов, когда событие может происходить или не осуществляться.
Слайд 6Случайной величиной
называется переменная
. величина, значение которой зависит от исхода некоторого испытания.
Дискретная Непрерывная
Дискретная Непрерывная
Слайд 7Дискретной называется случайная величина, которая может принимать значения некоторой конечной или
бесконечной числовой последовательности (число слов в тексте, студентов в аудитории, больных в клинике...)
Слайд 10Статистический ряд – результаты измерений для статистического исследования, записанные последовательно по
порядку их получения. Удобнее представить в таблице.
Х1, Х2, Х3………Хn
Х1, Х2, Х3………Хn
Слайд 11Распределение дискретной
случайной величины.
Дискретная случайная величина считается заданной, если указаны ее
возможные значения и соответствующие им вероятности
Слайд 15Различные распределения
1. Биномиальное распределение
(позволяет определить вероятность того, что событие А
произойдет m paз при n испытаниях).
Слайд 16
2. Распределение Максвелла (распределение молекул газа по скоростям, кинетическим энергиям).
График - кривая Максвелла.
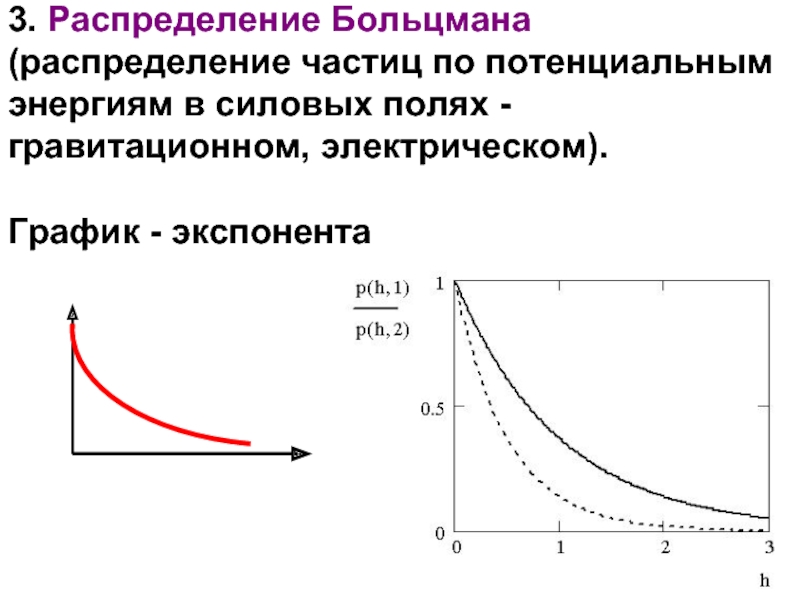
Слайд 173. Распределение Больцмана (распределение частиц по потенциальным энергиям в силовых полях
- гравитационном, электрическом).
График - экспонента
График - экспонента
Слайд 20Нормальный закон распределения имеет важное практическое значение в естественных науках. Оказывается,
распределение роста, массы новорожденных и много других случайных событий физической и биологической природы описываются нормальным законом распределения и графически иллюстрируются кривой Гаусса.
Слайд 221.Математическое ожидание случайной величины есть сумма произведений всех возможных ее значений
на вероятности этих значений:
Слайд 24
Если n велико , то относительные частоты
m/n = р,
а среднее арифметическое значение практически равно математическому ожиданию.
<Х> = М(х)
Математическое ожидание часто отождествляют со средним значением
<Х>
Слайд 25 3. Дисперсия случайной величины – это математическое ожидание квадрата отклонения
случайной величины от ее математического ожидания;
Слайд 26Дисперсия характеризует рассеяние случайных величин относительно математического ожидания.
125
130
120 150 180
120 150 180
Слайд 27Размерность дисперсии - квадрат размерности случайной величины, поэтому введена величина
4. σ - среднеквадратическое отклонение, которое имеет размерность случайной величины.
Слайд 28
Сравнительный анализ значений математического ожидания, дисперсии и среднеквадратического значения по графику
Слайд 30dP - вероятность того, что непрерывная случайная величина X принимает значения
между х и х± Δх
dP =f(x)dx
х – Δх х х+ Δх
dP =f(x)dx, где f(x) - плотность вероятности или функция распределения вероятности.
Слайд 31функция распределения вероятности показывает, как изменяется вероятность, отнесенная к интервалу dx
случайной величины в зависимости от значения самой этой величины: f (х) = dP/dx
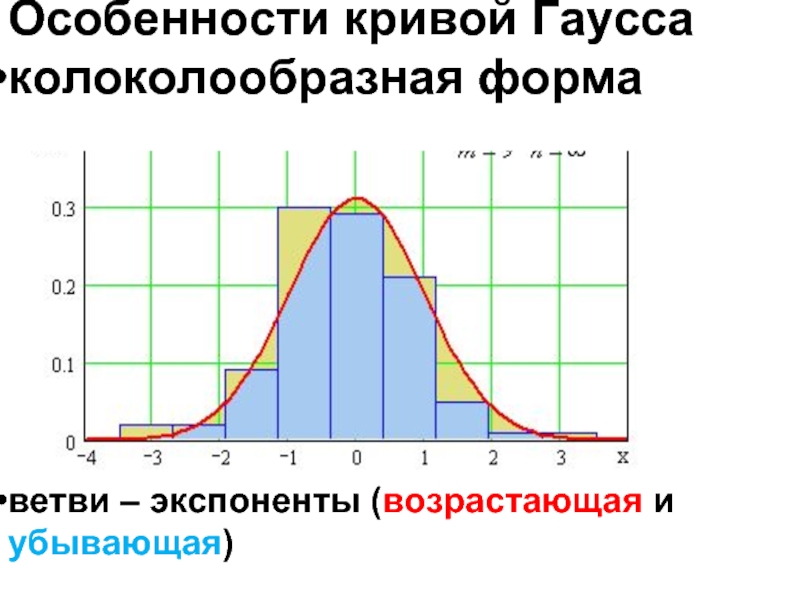
Слайд 42ветви – экспоненты (возрастающая и убывающая)
Особенности кривой Гаусса
колоколообразная форма
Слайд 50Вероятность появления случайной величины в интервале значений M(X)±3σ равна 99,97% Это
соответствует условию нормировки - площадь под кривой равна 1, т.е - практически все случайные величины нормального распределения находятся под кривой Гаусса.
Слайд 53Для нормального закона распределения характерен симметричный вид гистограммы
•Гистограмма частот - совокупность
смежных прямоугольников,
построенных на одной прямой линии.
Основания прямоугольников одинаковы.
Высоты прямоугольников равны относительной частоте m/n (вероятности).
построенных на одной прямой линии.
Основания прямоугольников одинаковы.
Высоты прямоугольников равны относительной частоте m/n (вероятности).
Слайд 55m/n
0,4
0,3
0,2
0,1
0
50 60 70 80 90 100 110 120 удар/мин
m/n
0,4
0,3
0,2
0,1
0
50 60 70 80 90 100 110 120 удар/мин
