- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Dense Linear Algebra: History and Structure, Parallel Matrix Multiplication презентация
Содержание
- 1. Dense Linear Algebra: History and Structure, Parallel Matrix Multiplication
- 2. 02/22/2011 CS267 Lecture 11 Outline History and
- 3. 02/22/2011 CS267 Lecture 11 Outline History and
- 4. Motifs The Motifs (formerly “Dwarfs”) from
- 5. What is dense linear algebra? Not just
- 6. A brief history of (Dense) Linear Algebra
- 7. 02/22/2011 CS267 Lecture 11 Current Records for
- 8. A brief history of (Dense) Linear Algebra
- 9. A brief history of (Dense) Linear Algebra
- 10. 02/25/2009 CS267 Lecture 8
- 11. A brief history of (Dense) Linear Algebra
- 12. A brief history of (Dense) Linear Algebra
- 13. 02/22/2011 CS267 Lecture 11 Success Stories for
- 14. Back to basics: Why avoiding communication
- 15. Why avoiding communication is important (2/2) Running
- 16. for i = 1 to n
- 17. Less Communication with Blocked Matrix Multiply Blocked
- 18. Blocked vs Cache-Oblivious Algorithms Blocked Matmul C
- 19. Communication Lower Bounds: Prior Work on
- 20. New lower bound for all “direct” linear
- 21. Can we attain these lower bounds? Do
- 22. A brief future look at (Dense) Linear
- 23. 02/22/2011 CS267 Lecture 11 Outline History and
- 24. What could go into the linear algebra
- 25. For all linear algebra problems: Ex: LAPACK
- 26. For all matrix/problem structures: Ex: LAPACK Table
- 27. For all matrix/problem structures: Ex: LAPACK Table
- 28. For all matrix/problem structures: Ex: LAPACK Table
- 29. For all matrix/problem structures: Ex: LAPACK Table
- 30. For all matrix/problem structures: Ex: LAPACK Table
- 31. For all matrix/problem structures: Ex: LAPACK Table
- 32. For all matrix/problem structures: Ex: LAPACK Table
- 33. For all matrix/problem structures: Ex: LAPACK Table
- 34. Organizing Linear Algebra – in books www.netlib.org/lapack www.netlib.org/scalapack www.cs.utk.edu/~dongarra/etemplates www.netlib.org/templates gams.nist.gov
- 35. 02/22/2011 CS267 Lecture 11 Outline History and
- 36. 02/22/2011 CS267 Lecture 11 Different Parallel Data
- 37. 02/22/2011 CS267 Lecture 11 Parallel Matrix-Vector Product
- 38. 02/22/2011 CS267 Lecture 11 Matrix-Vector Product
- 39. 02/22/2011 CS267 Lecture 11 Parallel Matrix Multiply
- 40. 02/22/2011 CS267 Lecture 11 Matrix Multiply with
- 41. 02/22/2011 CS267 Lecture 11 Matrix Multiply: 1D
- 42. 02/22/2011 CS267 Lecture 11 MatMul: 1D layout
- 43. 02/22/2011 CS267 Lecture 11 Naïve MatMul (continued)
- 44. 02/22/2011 CS267 Lecture 11 Matmul for 1D
- 45. 02/22/2011 CS267 Lecture 11 Matmul for 1D
- 46. 02/22/2011 CS267 Lecture 11 MatMul with 2D
- 47. 02/22/2011 CS267 Lecture 11 Cannon’s Algorithm …
- 48. 02/22/2011 CS267 Lecture 11 C(1,2) = A(1,0)
- 49. 02/22/2011 CS267 Lecture 11 Initial Step to
- 50. 02/22/2011 CS267 Lecture 11 Skewing Steps in
- 51. 02/22/2011 CS267 Lecture 11 Cost of Cannon’s
- 52. Cannon’s Algorithm is “optimal” Optimal means Considering
- 53. 02/22/2011 CS267 Lecture 11 Pros and Cons
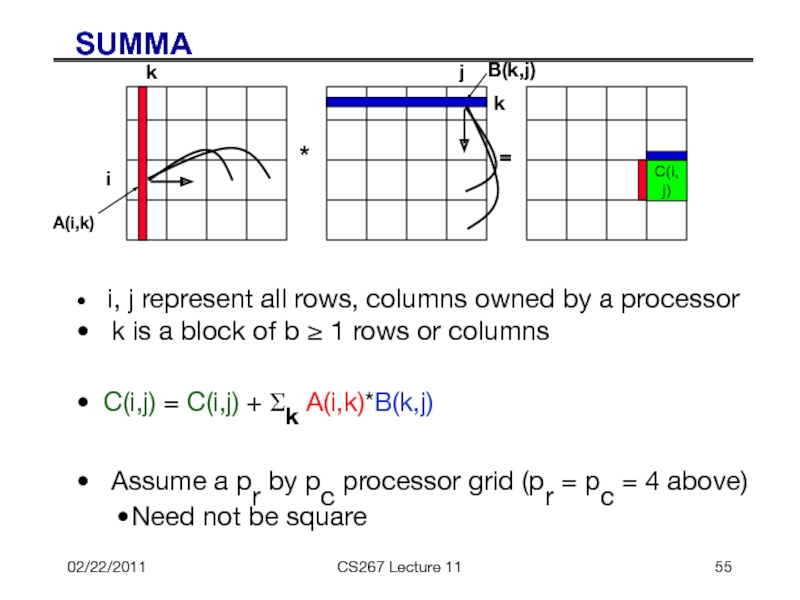
- 54. 02/22/2011 CS267 Lecture 11 SUMMA Algorithm SUMMA
- 55. 02/22/2011 CS267 Lecture 11 SUMMA
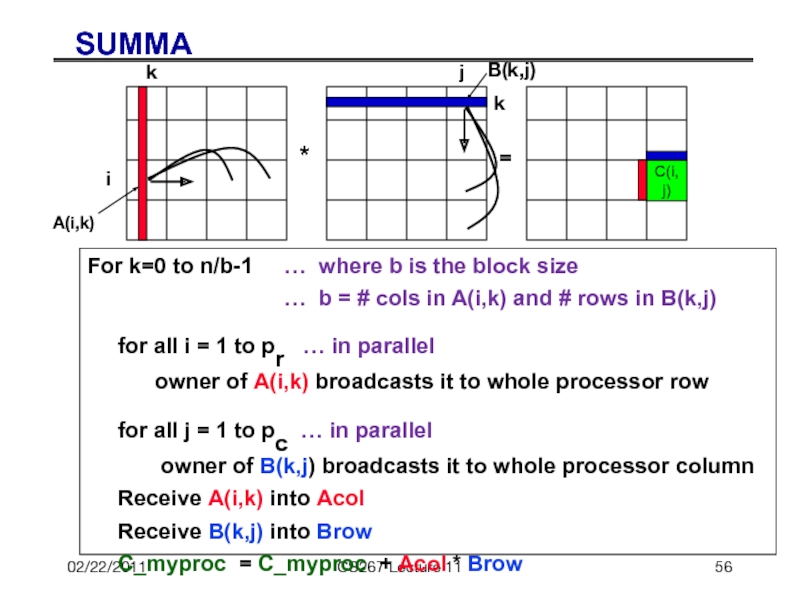
- 56. 02/22/2011 CS267 Lecture 11 SUMMA For
- 57. 02/22/2011 CS267 Lecture 11 SUMMA performance
- 58. 02/22/2011 CS267 Lecture 11 SUMMA performance
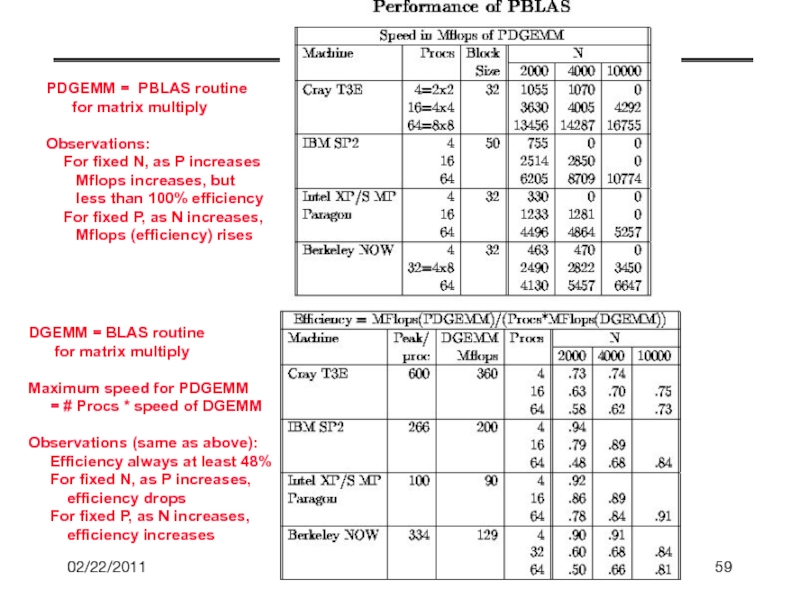
- 59. 02/22/2011 CS267 Lecture 8 PDGEMM = PBLAS
- 60. 02/22/2011 CS267 Lecture 11 Summary of Parallel
- 61. 02/22/2011 CS267 Lecture 11 Summary of Parallel
- 62. Beating #words_moved = Ω(n2/P1/2)
- 63. 2.5D algorithms – for c copies 3D
- 64. 2.5D matrix multiply Interpolate between
- 65. 2.5D matrix multiply performance Source: Edgar Solomonik
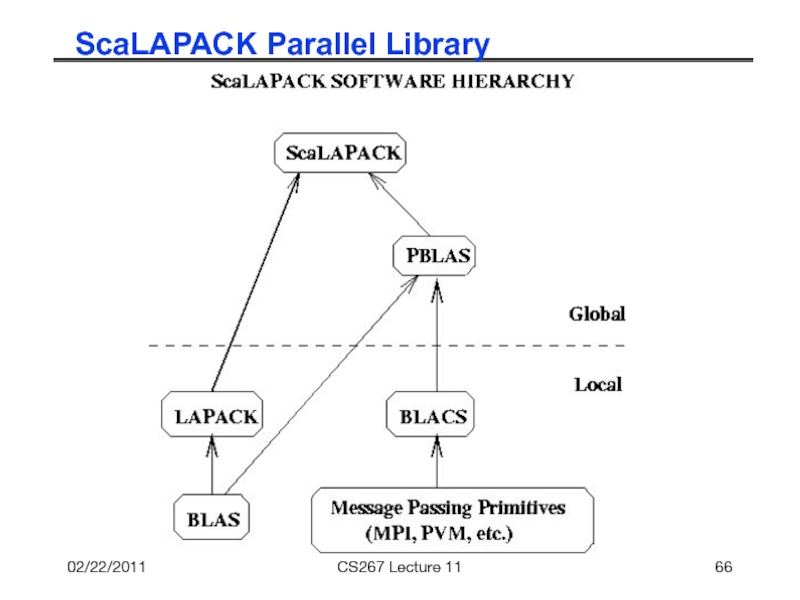
- 66. 02/22/2011 CS267 Lecture 11 ScaLAPACK Parallel Library
- 67. 02/22/2011 CS267 Lecture 11 Extra Slides
- 68. 2/27/08 CS267 Guest Lecture 1 Recursive Layouts
- 69. 02/09/2006 CS267 Lecture 8 Gaussian Elimination
- 70. 02/09/2006 CS267 Lecture 8 LU Algorithm:
- 71. 02/09/2006 CS267 Lecture 8 Recursive Factorizations Just
- 72. 02/09/2006 CS267 Lecture 8 LAPACK Recursive
- 73. 02/09/2006 CS267 Lecture 8 Review: BLAS 3
- 74. 02/09/2006 CS267 Lecture 8 Review: Row and
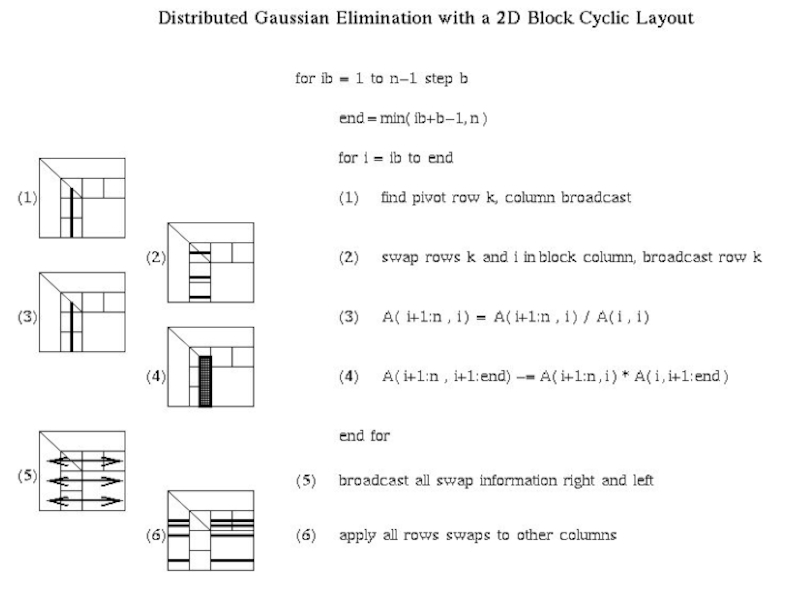
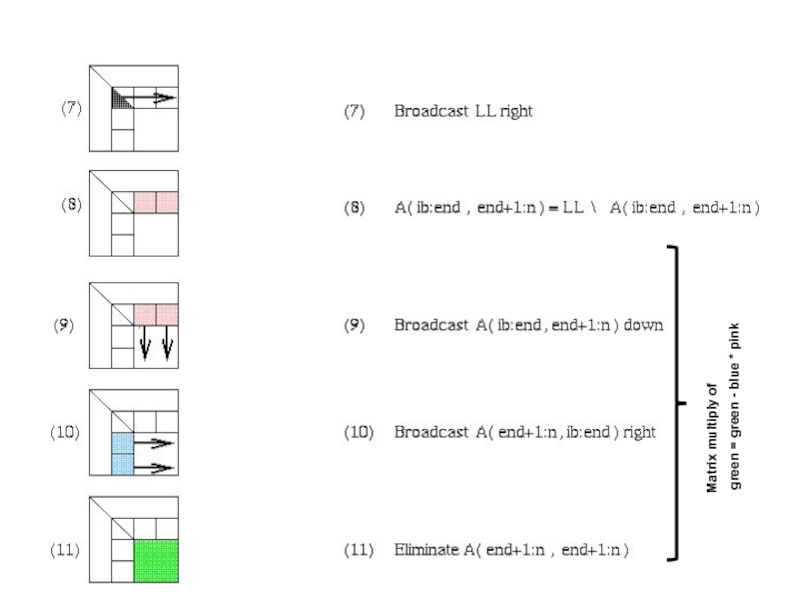
- 75. 02/09/2006 CS267 Lecture 8 Distributed GE with
- 76. 02/09/2006 CS267 Lecture 8 Distributed GE with a 2D Block Cyclic Layout
- 77. 02/09/2006 CS267 Lecture 8 Matrix multiply
- 78. 02/09/2006 CS267 Lecture 8 PDGESV = ScaLAPACK
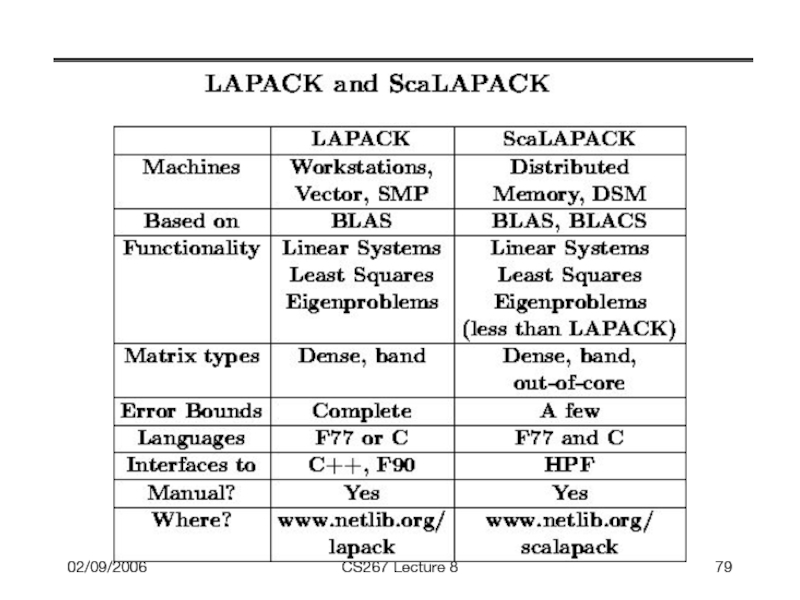
- 79. 02/09/2006 CS267 Lecture 8
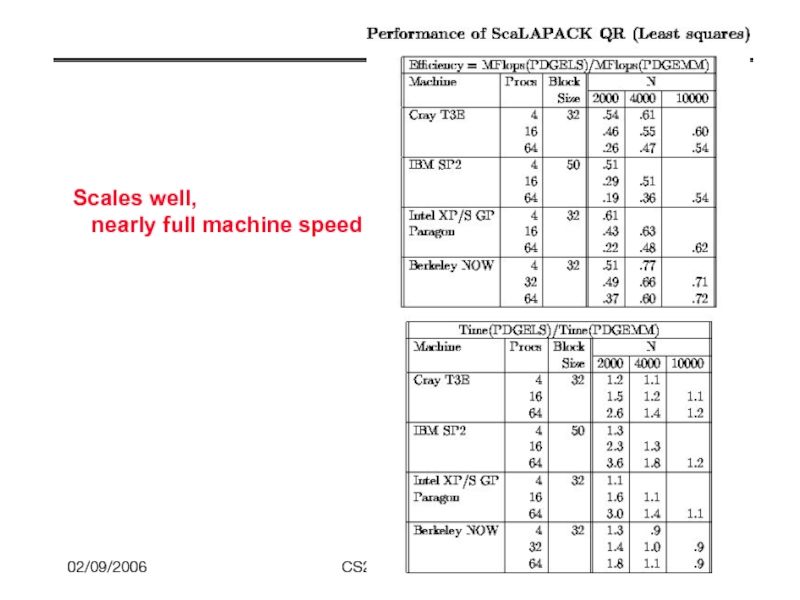
- 80. 02/09/2006 CS267 Lecture 8 Scales well, nearly full machine speed
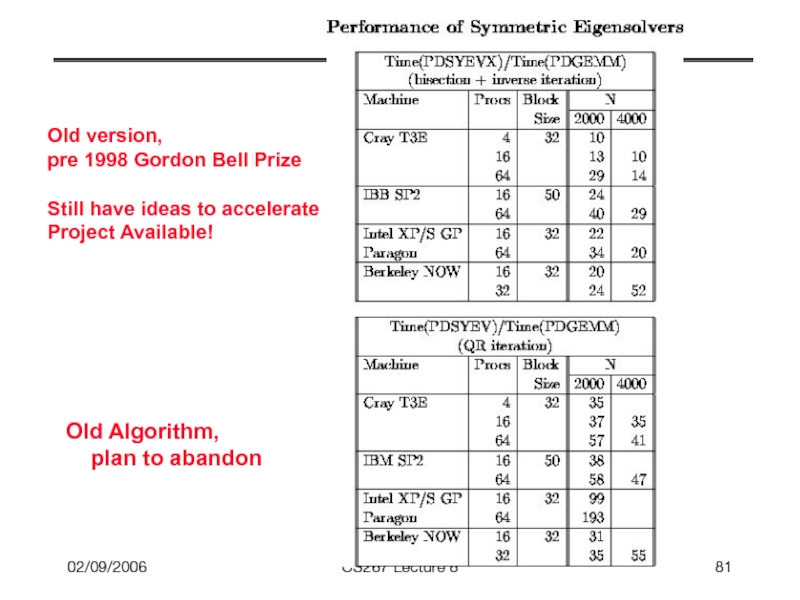
- 81. 02/09/2006 CS267 Lecture 8 Old version, pre
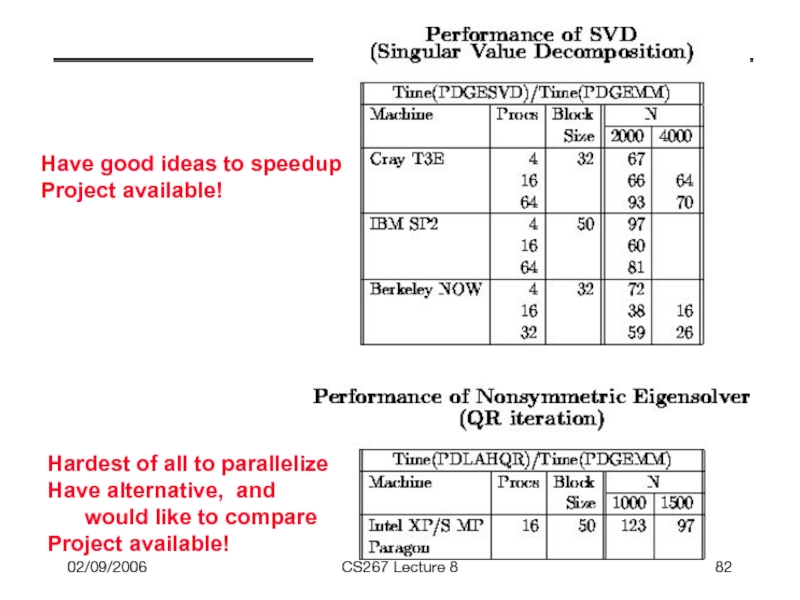
- 82. 02/09/2006 CS267 Lecture 8 Have good ideas
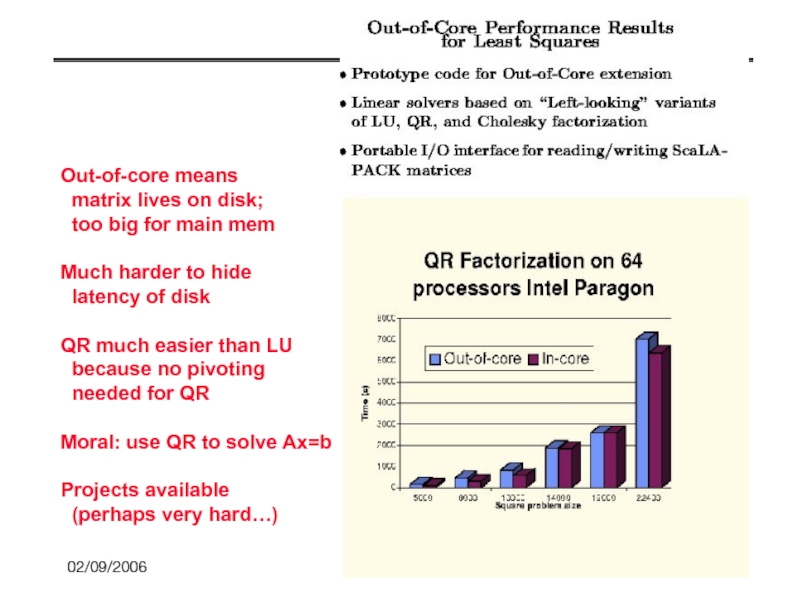
- 83. 02/09/2006 CS267 Lecture 8 Out-of-core means
- 84. 02/09/2006 CS267 Lecture 8 A small software project ...
- 85. 02/09/2006 CS267 Lecture 8 Work-Depth Model of
- 86. 02/09/2006 CS267 Lecture 8 Latency Bandwidth Model
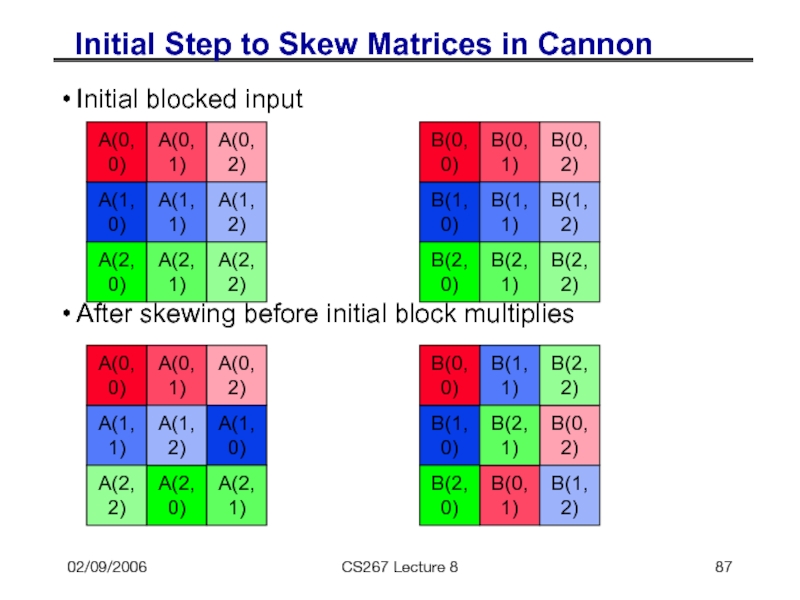
- 87. 02/09/2006 CS267 Lecture 8 Initial Step to
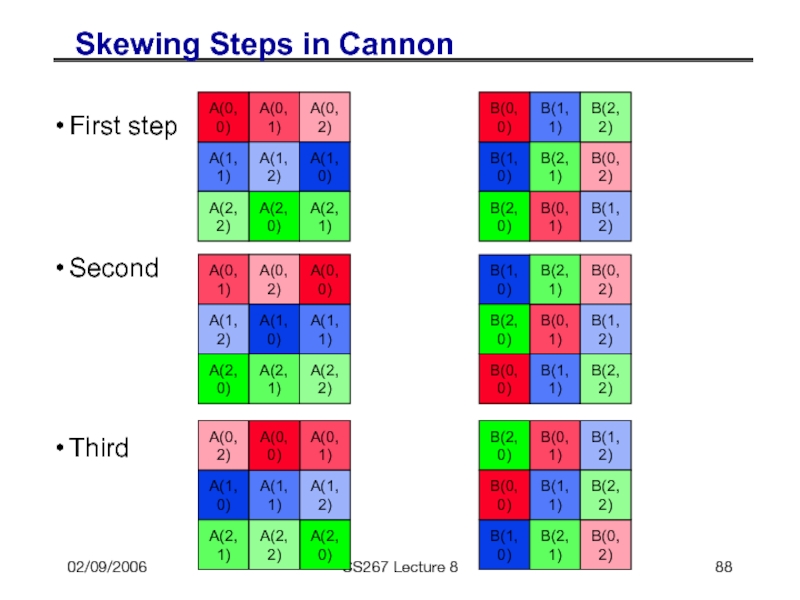
- 88. 02/09/2006 CS267 Lecture 8 Skewing Steps in
- 89. 2/25/2009 CS267 Lecture 8 Motivation (1) 3
- 90. 2/25/2009 CS267 Lecture 8 Motivation (2)
- 91. 02/25/2009 CS267 Lecture 8 Algorithms for 2D
- 92. Lessons and Questions (1) Structure of the
- 93. Organizing Linear Algebra (1) By Operations Low
- 94. Organizing Linear Algebra (2) By Data Type
- 95. For all linear algebra problems: Ex: LAPACK
- 96. For all matrix/problem structures: Ex: LAPACK Table
- 97. For all matrix/problem structures: Ex: LAPACK Table
- 98. For all matrix/problem structures: Ex: LAPACK Table
- 99. For all matrix/problem structures: Ex: LAPACK Table
- 100. For all matrix/problem structures: Ex: LAPACK Table
- 101. For all matrix/problem structures: Ex: LAPACK Table
- 102. For all matrix/problem structures: Ex: LAPACK Table
- 103. For all data types: Ex: LAPACK Table
- 104. Organizing Linear Algebra (3) www.netlib.org/lapack www.netlib.org/scalapack www.cs.utk.edu/~dongarra/etemplates www.netlib.org/templates gams.nist.gov
- 105. 2/27/08 CS267 Guest Lecture 1 Review of
Слайд 102/22/2011
CS267 Lecture 11
CS 267
Dense Linear Algebra:
History and Structure,
Parallel Matrix Multiplication
James Demmel
www.cs.berkeley.edu/~demmel/cs267_Spr11
Слайд 202/22/2011
CS267 Lecture 11
Outline
History and motivation
Structure of the Dense Linear Algebra motif
Parallel
Parallel Gaussian Elimination (next time)
Слайд 302/22/2011
CS267 Lecture 11
Outline
History and motivation
Structure of the Dense Linear Algebra motif
Parallel
Parallel Gaussian Elimination (next time)
Слайд 4Motifs
The Motifs (formerly “Dwarfs”) from
“The Berkeley View” (Asanovic et al.)
Motifs
Слайд 5What is dense linear algebra?
Not just matmul!
Linear Systems: Ax=b
Least Squares: choose
Overdetermined or underdetermined
Unconstrained, constrained, weighted
Eigenvalues and vectors of Symmetric Matrices
Standard (Ax = λx), Generalized (Ax=λBx)
Eigenvalues and vectors of Unsymmetric matrices
Eigenvalues, Schur form, eigenvectors, invariant subspaces
Standard, Generalized
Singular Values and vectors (SVD)
Standard, Generalized
Different matrix structures
Real, complex; Symmetric, Hermitian, positive definite; dense, triangular, banded …
Level of detail
Simple Driver
Expert Drivers with error bounds, extra-precision, other options
Lower level routines (“apply certain kind of orthogonal transformation”, matmul…)
CS267 Lecture 11
02/22/2011
Слайд 6A brief history of (Dense) Linear Algebra software (1/7)
Libraries like EISPACK
Then the BLAS (1) were invented (1973-1977)
Standard library of 15 operations (mostly) on vectors
“AXPY” ( y = α·x + y ), dot product, scale (x = α·x ), etc
Up to 4 versions of each (S/D/C/Z), 46 routines, 3300 LOC
Goals
Common “pattern” to ease programming, readability, self-documentation
Robustness, via careful coding (avoiding over/underflow)
Portability + Efficiency via machine specific implementations
Why BLAS 1 ? They do O(n1) ops on O(n1) data
Used in libraries like LINPACK (for linear systems)
Source of the name “LINPACK Benchmark” (not the code!)
02/22/2011
CS267 Lecture 11
In the beginning was the do-loop…
Слайд 702/22/2011
CS267 Lecture 11
Current Records for Solving Dense Systems (11/2010)
Linpack Benchmark
Fastest machine overall (www.top500.org)
Tianhe-1A (Tianjin, China)
Intel Xeon + NVIDIA GPUs + interconnect
2.57 Petaflops out of 4.7 Petaflops peak
n = 3.6M
n1/2 = 1.0M (size for half max performance)
186K cores, 4MW of power
Historical data (www.netlib.org/performance)
Palm Pilot III
1.69 Kiloflops
n = 100
Слайд 8A brief history of (Dense) Linear Algebra software (2/7)
But the BLAS-1
Consider AXPY ( y = α·x + y ): 2n flops on 3n read/writes
Computational intensity = (2n)/(3n) = 2/3
Too low to run near peak speed (read/write dominates)
Hard to vectorize (“SIMD’ize”) on supercomputers of the day (1980s)
So the BLAS-2 were invented (1984-1986)
Standard library of 25 operations (mostly) on matrix/vector pairs
“GEMV”: y = α·A·x + β·x, “GER”: A = A + α·x·yT, x = T-1·x
Up to 4 versions of each (S/D/C/Z), 66 routines, 18K LOC
Why BLAS 2 ? They do O(n2) ops on O(n2) data
So computational intensity still just ~(2n2)/(n2) = 2
OK for vector machines, but not for machine with caches
02/22/2011
CS267 Lecture 11
Слайд 9A brief history of (Dense) Linear Algebra software (3/7)
The next step:
Standard library of 9 operations (mostly) on matrix/matrix pairs
“GEMM”: C = α·A·B + β·C, C = α·A·AT + β·C, B = T-1·B
Up to 4 versions of each (S/D/C/Z), 30 routines, 10K LOC
Why BLAS 3 ? They do O(n3) ops on O(n2) data
So computational intensity (2n3)/(4n2) = n/2 – big at last!
Good for machines with caches, other mem. hierarchy levels
How much BLAS1/2/3 code so far (all at www.netlib.org/blas)
Source: 142 routines, 31K LOC, Testing: 28K LOC
Reference (unoptimized) implementation only
Ex: 3 nested loops for GEMM
Lots more optimized code (eg Homework 1)
Motivates “automatic tuning” of the BLAS
Part of standard math libraries (eg AMD AMCL, Intel MKL)
02/22/2011
CS267 Lecture 11
Слайд 11A brief history of (Dense) Linear Algebra software (4/7)
LAPACK – “Linear
Ex: Obvious way to express Gaussian Elimination (GE) is adding multiples of one row to other rows – BLAS-1
How do we reorganize GE to use BLAS-3 ? (details later)
Contents of LAPACK (summary)
Algorithms we can turn into (nearly) 100% BLAS 3
Linear Systems: solve Ax=b for x
Least Squares: choose x to minimize ||Ax-b||2
Algorithms that are only ≈50% BLAS 3
Eigenproblems: Find λ and x where Ax = λ x
Singular Value Decomposition (SVD)
Generalized problems (eg Ax = λ Bx)
Error bounds for everything
Lots of variants depending on A’s structure (banded, A=AT, etc)
How much code? (Release 3.3, Nov 2010) (www.netlib.org/lapack)
Source: 1586 routines, 500K LOC, Testing: 363K LOC
Ongoing development (at UCB and elsewhere) (class projects!)
02/22/2011
CS267 Lecture 11
Слайд 12A brief history of (Dense) Linear Algebra software (5/7)
Is LAPACK parallel?
Only
ScaLAPACK – “Scalable LAPACK” (1995 – now)
For distributed memory – uses MPI
More complex data structures, algorithms than LAPACK
Only (small) subset of LAPACK’s functionality available
Details later (class projects!)
All at www.netlib.org/scalapack
02/22/2011
CS267 Lecture 11
Слайд 1302/22/2011
CS267 Lecture 11
Success Stories for Sca/LAPACK (6/7)
Cosmic Microwave Background Analysis, BOOMERanG
ScaLAPACK
Widely used
Adopted by Mathworks, Cray, Fujitsu, HP, IBM, IMSL, Intel, NAG, NEC, SGI, …
5.5M webhits/year @ Netlib (incl. CLAPACK, LAPACK95)
New Science discovered through the solution of dense matrix systems
Nature article on the flat universe used ScaLAPACK
Other articles in Physics Review B that also use it
1998 Gordon Bell Prize
www.nersc.gov/news/reports/newNERSCresults050703.pdf
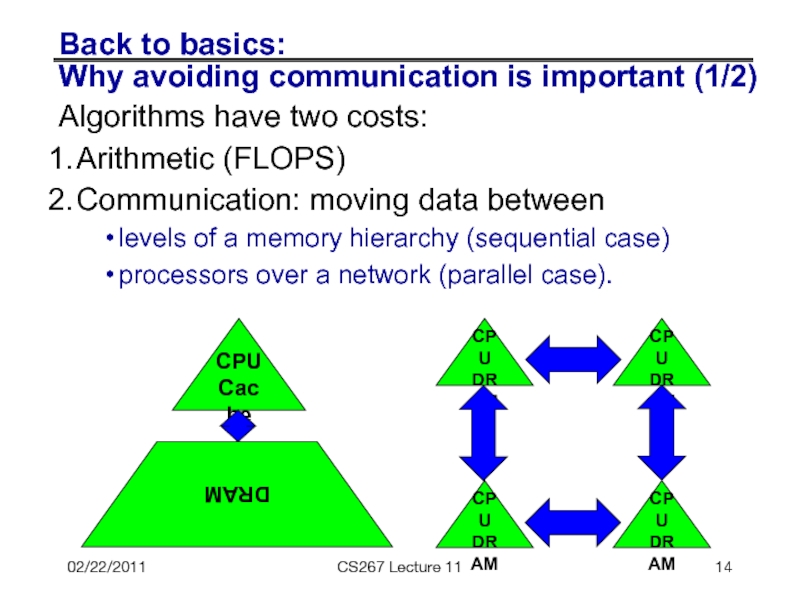
Слайд 14Back to basics:
Why avoiding communication is important (1/2)
Algorithms have two
Arithmetic (FLOPS)
Communication: moving data between
levels of a memory hierarchy (sequential case)
processors over a network (parallel case).
02/22/2011
CS267 Lecture 11
Слайд 15Why avoiding communication is important (2/2)
Running time of an algorithm is
# flops * time_per_flop
# words moved / bandwidth
# messages * latency
Time_per_flop << 1/ bandwidth << latency
Gaps growing exponentially with time
59%
02/22/2011
Слайд 16for i = 1 to n
{read row i of A
for j = 1 to n
{read C(i,j) into fast memory, n2 reads}
{read column j of B into fast memory, n3 reads}
for k = 1 to n
C(i,j) = C(i,j) + A(i,k) * B(k,j)
{write C(i,j) back to slow memory, n2 writes}
Review: Naïve Sequential MatMul: C = C + A*B
=
+
*
C(i,j)
A(i,:)
B(:,j)
C(i,j)
n3 + O(n2) reads/writes altogether
02/22/2011
CS267 Lecture 11
Слайд 17Less Communication with Blocked Matrix Multiply
Blocked Matmul C = A·B explicitly
… Break Anxn, Bnxn, Cnxn into bxb blocks labeled A(i,j), etc
… b chosen so 3 bxb blocks fit in cache
for i = 1 to n/b, for j=1 to n/b, for k=1 to n/b
C(i,j) = C(i,j) + A(i,k)·B(k,j) … b x b matmul, 4b2 reads/writes
(n/b)3 · 4b2 = 4n3/b reads/writes altogether
Minimized when 3b2 = cache size = M, yielding O(n3/M1/2) reads/writes
What if we had more levels of memory? (L1, L2, cache etc)?
Would need 3 more nested loops per level
02/22/2011
CS267 Lecture 11
Слайд 18Blocked vs Cache-Oblivious Algorithms
Blocked Matmul C = A·B explicitly refers to
… Break Anxn, Bnxn, Cnxn into bxb blocks labeled A(i,j), etc
… b chosen so 3 bxb blocks fit in cache
for i = 1 to n/b, for j=1 to n/b, for k=1 to n/b
C(i,j) = C(i,j) + A(i,k)·B(k,j) … b x b matmul
… another level of memory would need 3 more loops
Cache-oblivious Matmul C = A·B is independent of cache
Function C = RMM(A,B) … R for recursive
If A and B are 1x1
C = A · B
else … Break Anxn, Bnxn, Cnxn into (n/2)x(n/2) blocks labeled A(i,j), etc
for i = 1 to 2, for j = 1 to 2, for k = 1 to 2
C(i,j) = C(i,j) + RMM( A(i,k), B(k,j) ) … n/2 x n/2 matmul
02/22/2011
CS267 Lecture 11
Слайд 19Communication Lower Bounds: Prior Work on Matmul
Assume n3 algorithm (i.e.
Sequential case, with fast memory of size M
Lower bound on #words moved to/from slow memory = Ω (n3 / M1/2 ) [Hong, Kung, 81]
Attained using blocked or cache-oblivious algorithms
Parallel case on P processors:
Let NNZ be total memory needed; assume load balanced
Lower bound on #words moved = Ω (n3 /(p · NNZ1/2 )) [Irony, Tiskin, Toledo, 04]
If NNZ = 3n2/p (one copy of each matrix), then lower bound = Ω (n2 /p1/2 )
Attained by Cannon’s algorithm
02/22/2011
CS267 Lecture 11
Слайд 20New lower bound for all “direct” linear algebra
Holds for
BLAS, LU, QR,
Some whole programs (sequences of these operations, no matter how they are interleaved, eg computing Ak)
Dense and sparse matrices (where #flops << n3 )
Sequential and parallel algorithms
Some graph-theoretic algorithms (eg Floyd-Warshall)
Let M = “fast” memory size per processor
= cache size (sequential case) or O(n2/p) (parallel case)
#words_moved by at least one processor = Ω(#flops / M1/2 )
#messages_sent by at least one processor = Ω (#flops / M3/2 )
02/22/2011
CS267 Lecture 11
Слайд 21Can we attain these lower bounds?
Do conventional dense algorithms as implemented
Mostly not
If not, are there other algorithms that do?
Yes
Goals for algorithms:
Minimize #words = Ω (#flops/ M1/2 )
Minimize #messages = Ω (#flops/ M3/2 )
Need new data structures
Minimize for multiple memory hierarchy levels
Cache-oblivious algorithms would be simplest
Fewest flops when matrix fits in fastest memory
Cache-oblivious algorithms don’t always attain this
Attainable for nearly all dense linear algebra
Just a few prototype implementations so far (class projects!)
Only a few sparse algorithms so far (eg Cholesky)
02/22/2011
CS267 Lecture 11
Слайд 22A brief future look at (Dense) Linear Algebra software (7/7)
PLASMA and
Planned extensions to Multicore/GPU/Heterogeneous
Can one software infrastructure accommodate all algorithms and platforms of current (future) interest?
How much code generation and tuning can we automate?
Details later (Class projects!)
Other related projects
BLAST Forum (www.netlib.org/blas/blast-forum)
Attempt to extend BLAS to other languages, add some new functions, sparse matrices, extra-precision, interval arithmetic
Only partly successful (extra-precise BLAS used in latest LAPACK)
FLAME (www.cs.utexas.edu/users/flame/)
Formal Linear Algebra Method Environment
Attempt to automate code generation across multiple platforms
02/22/2011
CS267 Lecture 11
Слайд 2302/22/2011
CS267 Lecture 11
Outline
History and motivation
Structure of the Dense Linear Algebra motif
Parallel
Parallel Gaussian Elimination (next time)
Слайд 24What could go into the linear algebra motif(s)?
For all linear algebra
For all matrix/problem structures
For all data types
For all programming interfaces
Produce best algorithm(s) w.r.t.
performance and accuracy
(including error bounds, etc)
For all architectures and networks
Need to prioritize, automate!
CS267 Lecture 11
02/22/2011
Слайд 25For all linear algebra problems:
Ex: LAPACK Table of Contents
Linear Systems
Least Squares
Overdetermined,
Unconstrained, constrained, weighted
Eigenvalues and vectors of Symmetric Matrices
Standard (Ax = λx), Generalized (Ax=λBx)
Eigenvalues and vectors of Unsymmetric matrices
Eigenvalues, Schur form, eigenvectors, invariant subspaces
Standard, Generalized
Singular Values and vectors (SVD)
Standard, Generalized
Level of detail
Simple Driver
Expert Drivers with error bounds, extra-precision, other options
Lower level routines (“apply certain kind of orthogonal transformation”)
CS267 Lecture 11
02/22/2011
Слайд 26For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 27For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 28For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 29For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 30For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 31For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 32For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 33For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
CS267 Lecture 11
02/22/2011
Слайд 34Organizing Linear Algebra – in books
www.netlib.org/lapack
www.netlib.org/scalapack
www.cs.utk.edu/~dongarra/etemplates
www.netlib.org/templates
gams.nist.gov
Слайд 3502/22/2011
CS267 Lecture 11
Outline
History and motivation
Structure of the Dense Linear Algebra motif
Parallel
Parallel Gaussian Elimination (next time)
Слайд 3602/22/2011
CS267 Lecture 11
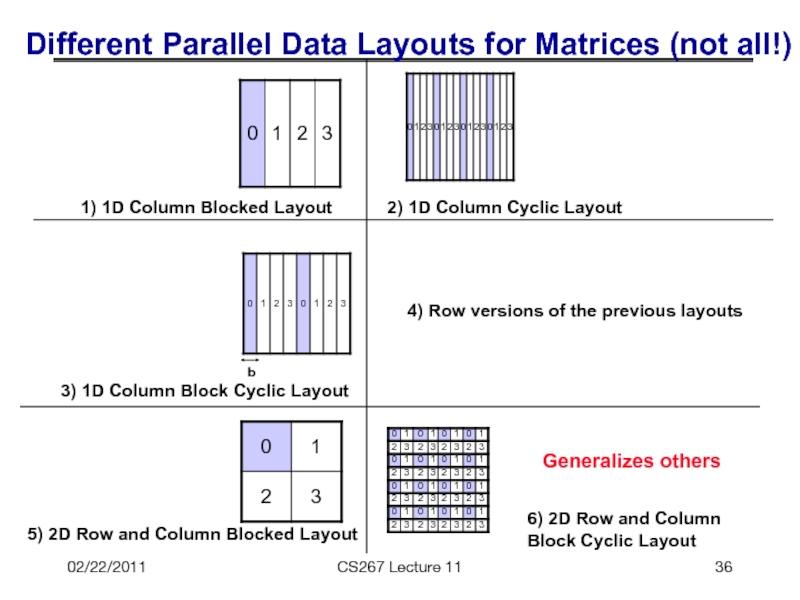
Different Parallel Data Layouts for Matrices (not all!)
1) 1D
2) 1D Column Cyclic Layout
3) 1D Column Block Cyclic Layout
4) Row versions of the previous layouts
Generalizes others
6) 2D Row and Column Block Cyclic Layout
5) 2D Row and Column Blocked Layout
b
Слайд 3702/22/2011
CS267 Lecture 11
Parallel Matrix-Vector Product
Compute y = y + A*x, where
Layout:
1D row blocked
A(i) refers to the n by n/p block row that processor i owns,
x(i) and y(i) similarly refer to segments of x,y owned by i
Algorithm:
Foreach processor i
Broadcast x(i)
Compute y(i) = A(i)*x
Algorithm uses the formula
y(i) = y(i) + A(i)*x = y(i) + Σj A(i,j)*x(j)
x
y
P0
P1
P2
P3
P0 P1 P2 P3
A(0)
A(1)
A(2)
A(3)
Слайд 3802/22/2011
CS267 Lecture 11
Matrix-Vector Product y = y + A*x
A column layout
But adds a reduction to update the destination y
A 2D blocked layout uses a broadcast and reduction, both on a subset of processors
sqrt(p) for square processor grid
P0 P1 P2 P3
P0 P1 P2 P3
P4 P5 P6 P7
P8 P9 P10 P11
P12 P13 P14 P15
Слайд 3902/22/2011
CS267 Lecture 11
Parallel Matrix Multiply
Computing C=C+A*B
Using basic algorithm: 2*n3 Flops
Variables are:
Data
Topology of machine
Scheduling communication
Use of performance models for algorithm design
Message Time = “latency” + #words * time-per-word
= α + n*β
Efficiency (in any model):
serial time / (p * parallel time)
perfect (linear) speedup ↔ efficiency = 1
Слайд 4002/22/2011
CS267 Lecture 11
Matrix Multiply with 1D Column Layout
Assume matrices are n
A(i) refers to the n by n/p block column that processor i owns (similiarly for B(i) and C(i))
B(i,j) is the n/p by n/p sublock of B(i)
in rows j*n/p through (j+1)*n/p - 1
Algorithm uses the formula
C(i) = C(i) + A*B(i) = C(i) + Σj A(j)*B(j,i)
May be a reasonable assumption for analysis, not for code
Слайд 4102/22/2011
CS267 Lecture 11
Matrix Multiply: 1D Layout on Bus or Ring
Algorithm uses
C(i) = C(i) + A*B(i) = C(i) + Σj A(j)*B(j,i)
First consider a bus-connected machine without broadcast: only one pair of processors can communicate at a time (ethernet)
Second consider a machine with processors on a ring: all processors may communicate with nearest neighbors simultaneously
Слайд 4202/22/2011
CS267 Lecture 11
MatMul: 1D layout on Bus without Broadcast
Naïve algorithm:
for i = 0 to p-1
for j = 0 to p-1 except i
if (myproc == i) send A(i) to processor j
if (myproc == j)
receive A(i) from processor i
C(myproc) = C(myproc) + A(i)*B(i,myproc)
barrier
Cost of inner loop:
computation: 2*n*(n/p)2 = 2*n3/p2
communication: α + β*n2 /p
Слайд 4302/22/2011
CS267 Lecture 11
Naïve MatMul (continued)
Cost of inner loop:
communication: α + β*n2 /p … approximately
Only 1 pair of processors (i and j) are active on any iteration,
and of those, only i is doing computation
=> the algorithm is almost entirely serial
Running time:
= (p*(p-1) + 1)*computation + p*(p-1)*communication
≈ 2*n3 + p2*α + p*n2*β
This is worse than the serial time and grows with p.
Слайд 4402/22/2011
CS267 Lecture 11
Matmul for 1D layout on a Processor Ring
Pairs of
Copy A(myproc) into Tmp
C(myproc) = C(myproc) + Tmp*B(myproc , myproc)
for j = 1 to p-1
Send Tmp to processor myproc+1 mod p
Receive Tmp from processor myproc-1 mod p
C(myproc) = C(myproc) + Tmp*B( myproc-j mod p , myproc)
Same idea as for gravity in simple sharks and fish algorithm
May want double buffering in practice for overlap
Ignoring deadlock details in code
Time of inner loop = 2*(α + β*n2/p) + 2*n*(n/p)2
Слайд 4502/22/2011
CS267 Lecture 11
Matmul for 1D layout on a Processor Ring
Time of
Total Time = 2*n* (n/p)2 + (p-1) * Time of inner loop
≈ 2*n3/p + 2*p*α + 2*β*n2
(Nearly) Optimal for 1D layout on Ring or Bus, even with Broadcast:
Perfect speedup for arithmetic
A(myproc) must move to each other processor, costs at least
(p-1)*cost of sending n*(n/p) words
Parallel Efficiency = 2*n3 / (p * Total Time)
= 1/(1 + α * p2/(2*n3) + β * p/(2*n) )
= 1/ (1 + O(p/n))
Grows to 1 as n/p increases (or α and β shrink)
But far from communication lower bound
Слайд 4602/22/2011
CS267 Lecture 11
MatMul with 2D Layout
Consider processors in 2D grid (physical
Processors can communicate with 4 nearest neighbors
Broadcast along rows and columns
Assume p processors form square s x s grid, s = p1/2
p(0,0) p(0,1) p(0,2)
p(1,0) p(1,1) p(1,2)
p(2,0) p(2,1) p(2,2)
p(0,0) p(0,1) p(0,2)
p(1,0) p(1,1) p(1,2)
p(2,0) p(2,1) p(2,2)
p(0,0) p(0,1) p(0,2)
p(1,0) p(1,1) p(1,2)
p(2,0) p(2,1) p(2,2)
=
*
Слайд 4702/22/2011
CS267 Lecture 11
Cannon’s Algorithm
… C(i,j) = C(i,j) + Σ A(i,k)*B(k,j)
… assume
forall i=0 to s-1 … “skew” A
left-circular-shift row i of A by i
… so that A(i,j) overwritten by A(i,(j+i)mod s)
forall i=0 to s-1 … “skew” B
up-circular-shift column i of B by i
… so that B(i,j) overwritten by B((i+j)mod s), j)
for k=0 to s-1 … sequential
forall i=0 to s-1 and j=0 to s-1 … all processors in parallel
C(i,j) = C(i,j) + A(i,j)*B(i,j)
left-circular-shift each row of A by 1
up-circular-shift each column of B by 1
k
Слайд 4802/22/2011
CS267 Lecture 11
C(1,2) = A(1,0) * B(0,2) + A(1,1) * B(1,2)
Cannon’s Matrix Multiplication
Слайд 4902/22/2011
CS267 Lecture 11
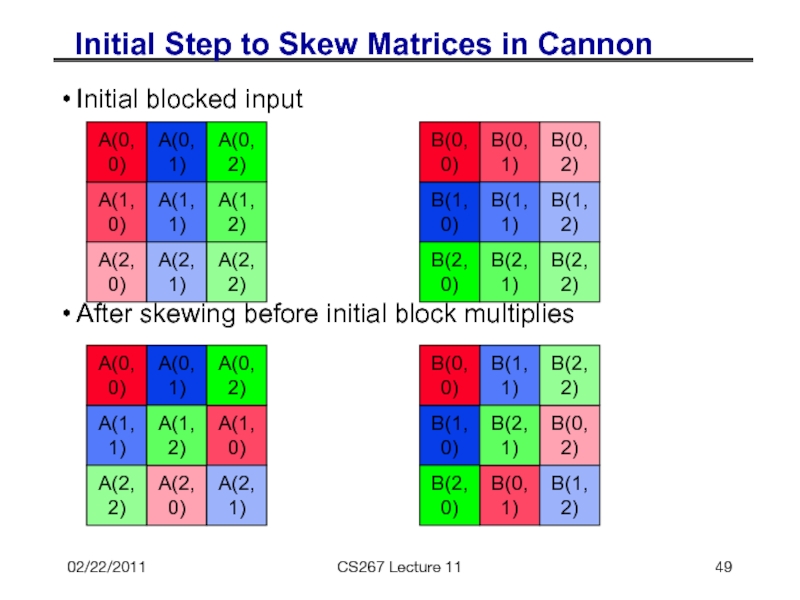
Initial Step to Skew Matrices in Cannon
Initial blocked input
After
A(1,0)
A(2,0)
A(0,1)
A(0,2)
A(1,1)
A(2,1)
A(1,2)
A(2,2)
A(0,0)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
A(1,0)
A(2,0)
A(0,1)
A(0,2)
A(1,1)
A(2,1)
A(1,2)
A(2,2)
A(0,0)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
Слайд 5002/22/2011
CS267 Lecture 11
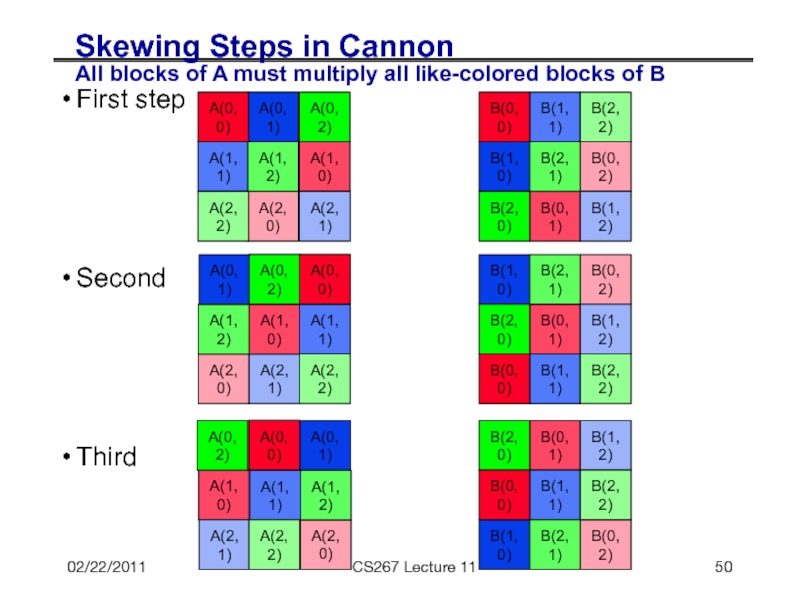
Skewing Steps in Cannon
All blocks of A must multiply
First step
Second
Third
A(1,0)
A(2,0)
A(0,1)
A(0,2)
A(2,1)
A(1,2)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
A(1,0)
A(2,0)
A(0,1)
A(0,2)
A(1,1)
A(2,1)
A(1,2)
A(2,2)
A(0,0)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
A(1,1)
A(2,2)
A(0,0)
Слайд 5102/22/2011
CS267 Lecture 11
Cost of Cannon’s Algorithm
forall i=0 to s-1
left-circular-shift row i of A by i … cost ≤ s*(α + β*n2/p)
forall i=0 to s-1
up-circular-shift column i of B by i … cost ≤ s*(α + β*n2/p)
for k=0 to s-1
forall i=0 to s-1 and j=0 to s-1
C(i,j) = C(i,j) + A(i,j)*B(i,j) … cost = 2*(n/s)3 = 2*n3/p3/2
left-circular-shift each row of A by 1 … cost = α + β*n2/p
up-circular-shift each column of B by 1 … cost = α + β*n2/p
Total Time = 2*n3/p + 4* s*α + 4*β*n2/s - Optimal!
Parallel Efficiency = 2*n3 / (p * Total Time)
= 1/( 1 + α * 2*(s/n)3 + β * 2*(s/n) )
= 1/(1 + O(sqrt(p)/n))
Grows to 1 as n/s = n/sqrt(p) = sqrt(data per processor) grows
Better than 1D layout, which had Efficiency = 1/(1 + O(p/n))
Слайд 52Cannon’s Algorithm is “optimal”
Optimal means
Considering only O(n3) matmul algs (not Strassen)
Considering
Use communication lower bound #words = Ω(#flops/M1/2)
Sequential: a processor doing n3 flops from matmul with a fast memory of size M must do Ω (n3 / M1/2 ) references to slow memory
Parallel: a processor doing f =#flops from matmul with a local memory of size M must do Ω (f / M1/2 ) references to remote memory
Local memory = O(n2/p) , f ≥ n3/p for at least one proc.
So f / M1/2 = Ω ((n3/p)/ (n2/p)1/2 ) = Ω ( n2/p1/2 )
#Messages = Ω ( #words sent / max message size) = Ω ( (n2/p1/2)/(n2/p)) = Ω (p1/2)
02/22/2011
CS267 Lecture 11
Слайд 5302/22/2011
CS267 Lecture 11
Pros and Cons of Cannon
So what if it’s “optimal”,
Local computation one call to (optimized) matrix-multiply
Hard to generalize for
p not a perfect square
A and B not square
Dimensions of A, B not perfectly divisible by s=sqrt(p)
A and B not “aligned” in the way they are stored on processors
block-cyclic layouts
Needs extra memory for copies of local matrices
Слайд 5402/22/2011
CS267 Lecture 11
SUMMA Algorithm
SUMMA = Scalable Universal Matrix Multiply
Slightly less
Presentation from van de Geijn and Watts
www.netlib.org/lapack/lawns/lawn96.ps
Similar ideas appeared many times
Used in practice in PBLAS = Parallel BLAS
www.netlib.org/lapack/lawns/lawn100.ps
Слайд 5502/22/2011
CS267 Lecture 11
SUMMA
*
=
i
j
A(i,k)
k
k
B(k,j)
i, j represent all rows, columns
k is a block of b ≥ 1 rows or columns
C(i,j) = C(i,j) + Σk A(i,k)*B(k,j)
Assume a pr by pc processor grid (pr = pc = 4 above)
Need not be square
C(i,j)
Слайд 5602/22/2011
CS267 Lecture 11
SUMMA
For k=0 to n/b-1 … where
… b = # cols in A(i,k) and # rows in B(k,j)
for all i = 1 to pr … in parallel
owner of A(i,k) broadcasts it to whole processor row
for all j = 1 to pc … in parallel
owner of B(k,j) broadcasts it to whole processor column
Receive A(i,k) into Acol
Receive B(k,j) into Brow
C_myproc = C_myproc + Acol * Brow
*
=
i
j
A(i,k)
k
k
B(k,j)
C(i,j)
Слайд 5702/22/2011
CS267 Lecture 11
SUMMA performance
For k=0 to n/b-1
for
owner of A(i,k) broadcasts it to whole processor row
… time = log s *( α + β * b*n/s), using a tree
for all j = 1 to s
owner of B(k,j) broadcasts it to whole processor column
… time = log s *( α + β * b*n/s), using a tree
Receive A(i,k) into Acol
Receive B(k,j) into Brow
C_myproc = C_myproc + Acol * Brow
… time = 2*(n/s)2*b
Total time = 2*n3/p + α * log p * n/b + β * log p * n2 /s
To simplify analysis only, assume s = sqrt(p)
Слайд 5802/22/2011
CS267 Lecture 11
SUMMA performance
Total time = 2*n3/p +
Parallel Efficiency =
1/(1 + α * log p * p / (2*b*n2) + β * log p * s/(2*n) )
≈Same β term as Cannon, except for log p factor
log p grows slowly so this is ok
Latency (α) term can be larger, depending on b
When b=1, get α * log p * n
As b grows to n/s, term shrinks to
α * log p * s (log p times Cannon)
Temporary storage grows like 2*b*n/s
Can change b to tradeoff latency cost with memory
Слайд 5902/22/2011
CS267 Lecture 8
PDGEMM = PBLAS routine
for matrix multiply
Observations:
Mflops increases, but
less than 100% efficiency
For fixed P, as N increases,
Mflops (efficiency) rises
DGEMM = BLAS routine
for matrix multiply
Maximum speed for PDGEMM
= # Procs * speed of DGEMM
Observations (same as above):
Efficiency always at least 48%
For fixed N, as P increases,
efficiency drops
For fixed P, as N increases,
efficiency increases
Слайд 6002/22/2011
CS267 Lecture 11
Summary of Parallel Matrix Multiplication so far
1D Layout
Bus without
Nearest neighbor communication on a ring (or bus with broadcast): Efficiency = 1/(1 + O(p/n))
2D Layout – one copy of all matrices (O(n2/p) per processor)
Cannon
Efficiency = 1/(1+O(α * ( sqrt(p) /n)3 +β* sqrt(p) /n)) – optimal!
Hard to generalize for general p, n, block cyclic, alignment
SUMMA
Efficiency = 1/(1 + O(α * log p * p / (b*n2) + β*log p * sqrt(p) /n))
Very General
b small => less memory, lower efficiency
b large => more memory, high efficiency
Used in practice (PBLAS)
Can we do better?
Слайд 6102/22/2011
CS267 Lecture 11
Summary of Parallel Matrix Multiplication so far
1D Layout
Bus without
Nearest neighbor communication on a ring (or bus with broadcast): Efficiency = 1/(1 + O(p/n))
2D Layout – one copy of all matrices (O(n2/p) per processor)
Cannon
Efficiency = 1/(1+O(α * ( sqrt(p) /n)3 +β* sqrt(p) /n)) – optimal!
Hard to generalize for general p, n, block cyclic, alignment
SUMMA
Efficiency = 1/(1 + O(α * log p * p / (b*n2) + β*log p * sqrt(p) /n))
Very General
b small => less memory, lower efficiency
b large => more memory, high efficiency
Used in practice (PBLAS)
Can we do better?
Why?
Слайд 62Beating #words_moved = Ω(n2/P1/2)
“3D Matmul” Algorithm on
Broadcast A in j direction (P1/3 redundant copies)
Broadcast B in i direction (ditto)
Local multiplies
Reduce (sum) in k direction
Communication volume
= O( (n/P1/3)2 ) - optimal
Number of messages
= O(log(P)) – optimal
What if we don’t have
memory for P1/3 copies?
#words_moved = Ω((n3/P)/local_mem1/2)
If one copy of data, local_mem = n2/P
Can we use more memory to communicate less?
Слайд 632.5D algorithms – for c copies
3D
2.5D
If 1 ≤ c ≤ p1/3
#words_moved = Ω(n2 /(c·p)1/2 )
#messages = Ω(p1/2 / c3/2 )
Both lower bounds (nearly) attained
2.5D algorithm “interpolates” between
2D (Cannon) and 3D algorithms
Source: Edgar Solomonik
Слайд 642.5D matrix multiply
Interpolate between
Cannon and 3D matmul
Replicate
Do p1/2/c3/2 steps of Cannon
on each copy of A,B
Sum contributions to C
from all c layers
#words_moved = O( n2 / (cp)1/2 )
#messages = O( p1/2/c3/2 + log(c) )
Source: Edgar Solomonik
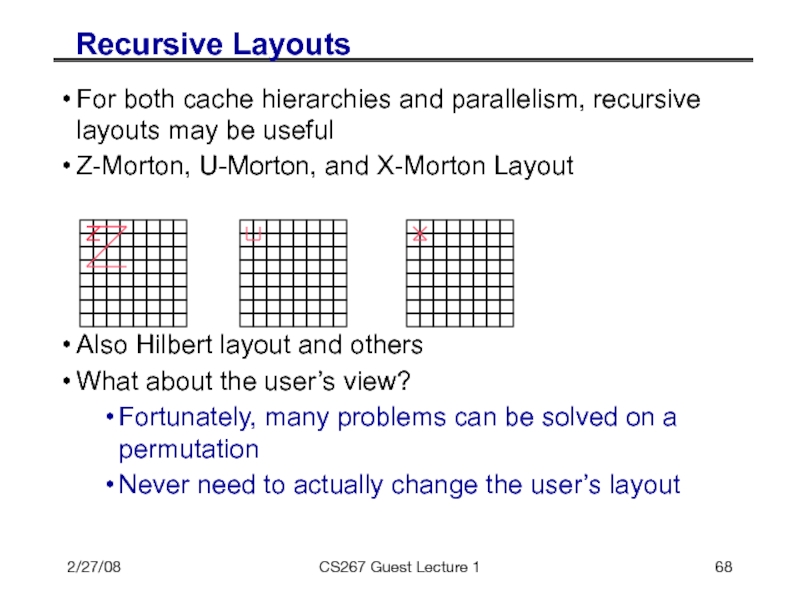
Слайд 682/27/08
CS267 Guest Lecture 1
Recursive Layouts
For both cache hierarchies and parallelism, recursive
Z-Morton, U-Morton, and X-Morton Layout
Also Hilbert layout and others
What about the user’s view?
Fortunately, many problems can be solved on a permutation
Never need to actually change the user’s layout
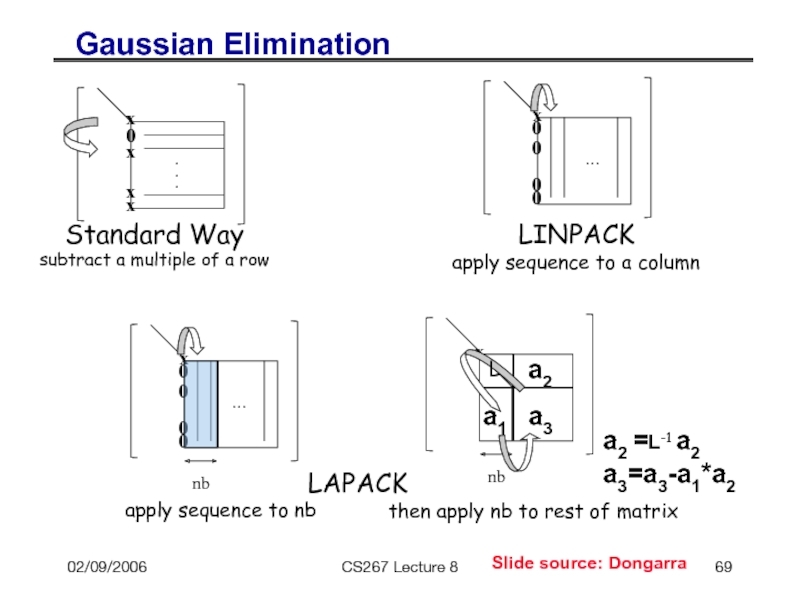
Слайд 6902/09/2006
CS267 Lecture 8
Gaussian Elimination
0
x
x
x
x
.
.
.
Standard Way
subtract a multiple of a row
Slide source:
Слайд 7002/09/2006
CS267 Lecture 8
LU Algorithm:
1: Split matrix into two rectangles
if only 1 column, scale by reciprocal of pivot & return
2: Apply LU Algorithm to the left part
3: Apply transformations to right part
(triangular solve A12 = L-1A12 and
matrix multiplication A22=A22 -A21*A12 )
4: Apply LU Algorithm to right part
Gaussian Elimination via a Recursive Algorithm
F. Gustavson and S. Toledo
Most of the work in the matrix multiply
Matrices of size n/2, n/4, n/8, …
Slide source: Dongarra
Слайд 7102/09/2006
CS267 Lecture 8
Recursive Factorizations
Just as accurate as conventional method
Same number of
Automatic variable blocking
Level 1 and 3 BLAS only !
Extreme clarity and simplicity of expression
Highly efficient
The recursive formulation is just a rearrangement of the point-wise LINPACK algorithm
The standard error analysis applies (assuming the matrix operations are computed the “conventional” way).
Slide source: Dongarra
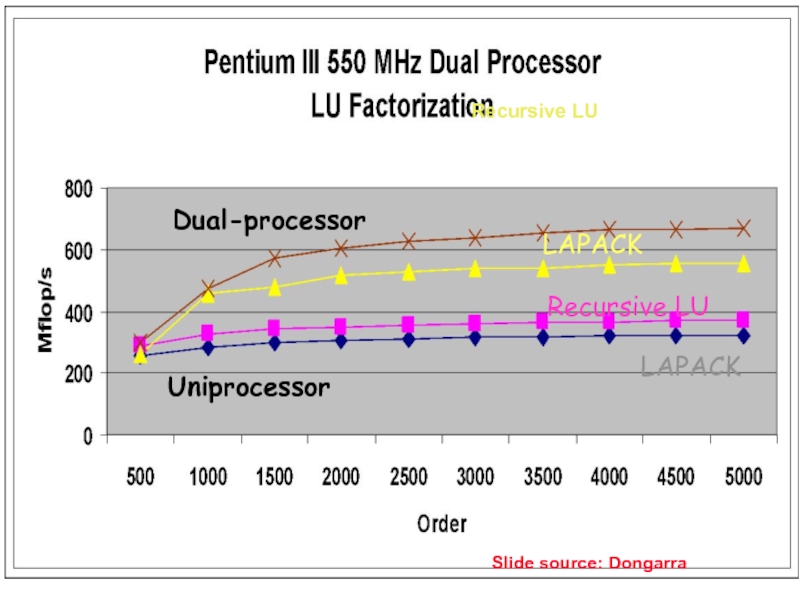
Слайд 7202/09/2006
CS267 Lecture 8
LAPACK
Recursive LU
Recursive LU
LAPACK
Dual-processor
Uniprocessor
Slide source: Dongarra
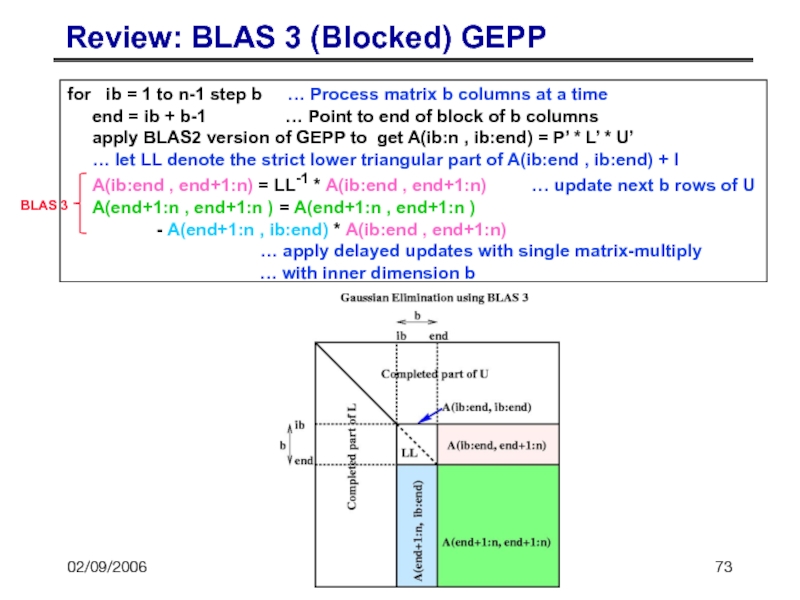
Слайд 7302/09/2006
CS267 Lecture 8
Review: BLAS 3 (Blocked) GEPP
for ib = 1
end = ib + b-1 … Point to end of block of b columns
apply BLAS2 version of GEPP to get A(ib:n , ib:end) = P’ * L’ * U’
… let LL denote the strict lower triangular part of A(ib:end , ib:end) + I
A(ib:end , end+1:n) = LL-1 * A(ib:end , end+1:n) … update next b rows of U
A(end+1:n , end+1:n ) = A(end+1:n , end+1:n )
- A(end+1:n , ib:end) * A(ib:end , end+1:n)
… apply delayed updates with single matrix-multiply
… with inner dimension b
BLAS 3
Слайд 7402/09/2006
CS267 Lecture 8
Review: Row and Column Block Cyclic Layout
processors and matrix
are distributed in a 2d array
pcol-fold parallelism
in any column, and calls to the
BLAS2 and BLAS3 on matrices of
size brow-by-bcol
serial bottleneck is eased
need not be symmetric in rows and
columns
Слайд 7502/09/2006
CS267 Lecture 8
Distributed GE with a 2D Block Cyclic Layout
block size
and bcol in the layout satisfy b=brow=bcol.
shaded regions indicate busy processors or
communication performed.
unnecessary to have a barrier between each
step of the algorithm, e.g.. step 9, 10, and 11 can be
pipelined
Слайд 7802/09/2006
CS267 Lecture 8
PDGESV = ScaLAPACK
parallel LU
Since it can run no faster than its
inner loop (PDGEMM), we measure:
Efficiency =
Speed(PDGESV)/Speed(PDGEMM)
Observations:
Efficiency well above 50% for large
enough problems
For fixed N, as P increases,
efficiency decreases
(just as for PDGEMM)
For fixed P, as N increases
efficiency increases
(just as for PDGEMM)
From bottom table, cost of solving
Ax=b about half of matrix multiply
for large enough matrices.
From the flop counts we would
expect it to be (2*n3)/(2/3*n3) = 3
times faster, but communication
makes it a little slower.
Слайд 8102/09/2006
CS267 Lecture 8
Old version,
pre 1998 Gordon Bell Prize
Still have ideas to
Project Available!
Old Algorithm,
plan to abandon
Слайд 8202/09/2006
CS267 Lecture 8
Have good ideas to speedup
Project available!
Hardest of all to
Have alternative, and
would like to compare
Project available!
Слайд 8302/09/2006
CS267 Lecture 8
Out-of-core means
matrix lives on disk;
too big for
Much harder to hide
latency of disk
QR much easier than LU
because no pivoting
needed for QR
Moral: use QR to solve Ax=b
Projects available
(perhaps very hard…)
Слайд 8502/09/2006
CS267 Lecture 8
Work-Depth Model of Parallelism
The work depth model:
The simplest model
For algorithm design, independent of a machine
The work, W, is the total number of operations
The depth, D, is the longest chain of dependencies
The parallelism, P, is defined as W/D
Specific examples include:
circuit model, each input defines a graph with ops at nodes
vector model, each step is an operation on a vector of elements
language model, where set of operations defined by language
Слайд 8602/09/2006
CS267 Lecture 8
Latency Bandwidth Model
Network of fixed number P of processors
fully
each with local memory
Latency (α)
accounts for varying performance with number of messages
gap (g) in logP model may be more accurate cost if messages are pipelined
Inverse bandwidth (β)
accounts for performance varying with volume of data
Efficiency (in any model):
serial time / (p * parallel time)
perfect (linear) speedup ? efficiency = 1
Слайд 8702/09/2006
CS267 Lecture 8
Initial Step to Skew Matrices in Cannon
Initial blocked input
After
A(0,1)
A(0,2)
A(1,0)
A(2,0)
A(1,1)
A(1,2)
A(2,1)
A(2,2)
A(0,0)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
A(0,1)
A(0,2)
A(1,0)
A(2,0)
A(1,1)
A(1,2)
A(2,1)
A(2,2)
A(0,0)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
Слайд 8802/09/2006
CS267 Lecture 8
Skewing Steps in Cannon
First step
Second
Third
A(0,1)
A(0,2)
A(1,0)
A(2,0)
A(1,1)
A(1,2)
A(2,1)
A(2,2)
A(0,0)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
A(0,1)
A(0,2)
A(1,0)
A(2,0)
A(1,2)
A(2,1)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
A(0,1)
A(0,2)
A(1,0)
A(2,0)
A(1,1)
A(1,2)
A(2,1)
A(2,2)
A(0,0)
B(0,1)
B(0,2)
B(1,0)
B(2,0)
B(1,1)
B(1,2)
B(2,1)
B(2,2)
B(0,0)
A(1,1)
A(2,2)
A(0,0)
Слайд 892/25/2009
CS267 Lecture 8
Motivation (1)
3 Basic Linear Algebra Problems
Linear Equations: Solve Ax=b
Least Squares: Find x that minimizes ||r||2 ≡ √Σ ri2 where r=Ax-b
Statistics: Fitting data with simple functions
3a. Eigenvalues: Find λ and x where Ax = λ x
Vibration analysis, e.g., earthquakes, circuits
3b. Singular Value Decomposition: ATAx=σ2x
Data fitting, Information retrieval
Lots of variations depending on structure of A
A symmetric, positive definite, banded, …
Слайд 902/25/2009
CS267 Lecture 8
Motivation (2)
Why dense A, as opposed to sparse
Many large matrices are sparse, but …
Dense algorithms easier to understand
Some applications yields large dense matrices
LINPACK Benchmark (www.top500.org)
“How fast is your computer?” = “How fast can you solve dense Ax=b?”
Large sparse matrix algorithms often yield smaller (but still large) dense problems
Do ParLab Apps most use small dense matrices?
Слайд 9102/25/2009
CS267 Lecture 8
Algorithms for 2D (3D) Poisson Equation (N = n2
Algorithm Serial PRAM Memory #Procs
Dense LU N3 N N2 N2
Band LU N2 (N7/3) N N3/2 (N5/3) N (N4/3)
Jacobi N2 (N5/3) N (N2/3) N N
Explicit Inv. N2 log N N2 N2
Conj.Gradients N3/2 (N4/3) N1/2(1/3) *log N N N
Red/Black SOR N3/2 (N4/3) N1/2 (N1/3) N N
Sparse LU N3/2 (N2) N1/2 N*log N (N4/3) N
FFT N*log N log N N N
Multigrid N log2 N N N
Lower bound N log N N
PRAM is an idealized parallel model with zero cost communication
Reference: James Demmel, Applied Numerical Linear Algebra, SIAM, 1997
(Note: corrected complexities for 3D case from last lecture!).
Слайд 92Lessons and Questions (1)
Structure of the problem matters
Cost of solution can
Many other examples
Some structure can be figured out automatically
“A\b” can figure out symmetry, some sparsity
Some structures known only to (smart) user
If performance not critical, user may be happy to settle for A\b
How much of this goes into the motifs?
How much should we try to help user choose?
Tuning, but at algorithmic choice level (SALSA)
Motifs overlap
Dense, sparse, (un)structured grids, spectral
Слайд 93Organizing Linear Algebra (1)
By Operations
Low level (eg mat-mul: BLAS)
Standard level (eg
Applications level (eg systems & control: SLICOT)
By Performance/accuracy tradeoffs
“Direct methods” with guarantees vs “iterative methods” that may work faster and accurately enough
By Structure
Storage
Dense
columnwise, rowwise, 2D block cyclic, recursive space-filling curves
Banded, sparse (many flavors), black-box, …
Mathematical
Symmetries, positive definiteness, conditioning, …
As diverse as the world being modeled
Слайд 94Organizing Linear Algebra (2)
By Data Type
Real vs Complex
Floating point (fixed or
By Target Platform
Serial, manycore, GPU, distributed memory, out-of-DRAM, Grid, …
By programming interface
Language bindings
“A\b” versus access to details
Слайд 95For all linear algebra problems:
Ex: LAPACK Table of Contents
Linear Systems
Least Squares
Overdetermined,
Unconstrained, constrained, weighted
Eigenvalues and vectors of Symmetric Matrices
Standard (Ax = λx), Generallzed (Ax=λxB)
Eigenvalues and vectors of Unsymmetric matrices
Eigenvalues, Schur form, eigenvectors, invariant subspaces
Standard, Generalized
Singular Values and vectors (SVD)
Standard, Generalized
Level of detail
Simple Driver
Expert Drivers with error bounds, extra-precision, other options
Lower level routines (“apply certain kind of orthogonal transformation”)
Слайд 96For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
Слайд 97For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
Слайд 98For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
Слайд 99For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
Слайд 100For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
Слайд 101For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general , pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
Слайд 102For all matrix/problem structures:
Ex: LAPACK Table of Contents
BD – bidiagonal
GB –
GE – general
GG – general, pair
GT – tridiagonal
HB – Hermitian banded
HE – Hermitian
HG – upper Hessenberg, pair
HP – Hermitian, packed
HS – upper Hessenberg
OR – (real) orthogonal
OP – (real) orthogonal, packed
PB – positive definite, banded
PO – positive definite
PP – positive definite, packed
PT – positive definite, tridiagonal
SB – symmetric, banded
SP – symmetric, packed
ST – symmetric, tridiagonal
SY – symmetric
TB – triangular, banded
TG – triangular, pair
TB – triangular, banded
TP – triangular, packed
TR – triangular
TZ – trapezoidal
UN – unitary
UP – unitary packed
Слайд 103For all data types:
Ex: LAPACK Table of Contents
Real and complex
Single and
Arbitrary precision in progress
Слайд 104Organizing Linear Algebra (3)
www.netlib.org/lapack
www.netlib.org/scalapack
www.cs.utk.edu/~dongarra/etemplates
www.netlib.org/templates
gams.nist.gov
Слайд 1052/27/08
CS267 Guest Lecture 1
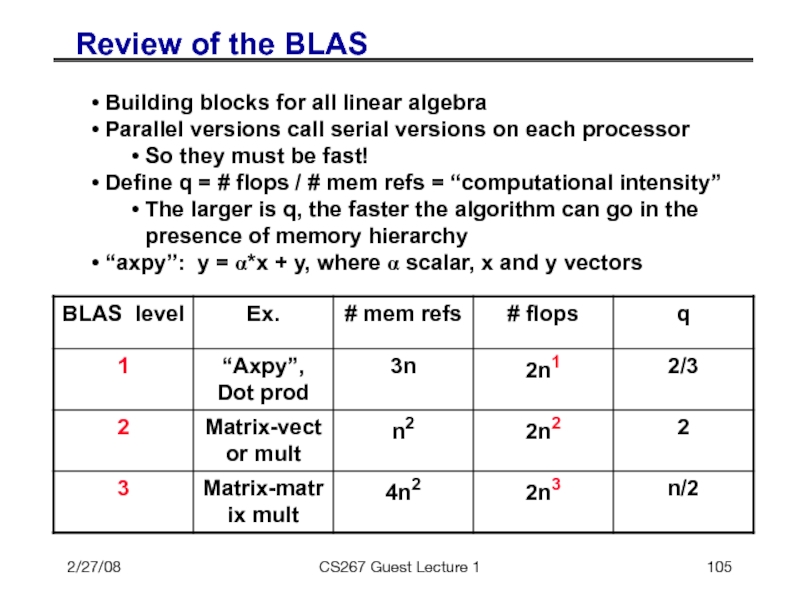
Review of the BLAS
Building blocks for all
Parallel versions call serial versions on each processor
So they must be fast!
Define q = # flops / # mem refs = “computational intensity”
The larger is q, the faster the algorithm can go in the
presence of memory hierarchy
“axpy”: y = α*x + y, where α scalar, x and y vectors