- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Спецификация уравнения множественной регрессии. Выбор переменных презентация
Содержание
- 1. Спецификация уравнения множественной регрессии. Выбор переменных
- 2. Спецификация уравнения регрессии Выбор переменных Выбор формы зависимости (следующая лекция)
- 3. Цели лекции 1. Рассмотрение проблемы спецификации переменных
- 4. Выбор переменных множественной регрессии Включение и исключение
- 5. Последствия не включения в уравнение существенной переменной
- 6. Последствия не включения в уравнение существенной переменной
- 7. Отсутствие существенной переменной Если объясняющая переменная X2
- 8. Отсутствие существенной переменной Оценка смещения коэффициента Направление
- 9. Отсутствие существенной переменной Направление смещения коэффициента 1.
- 10. Отсутствие существенной переменной Направление смещения коэффициента Коэффициент
- 11. Последствия включения в уравнение несущественной переменной Переменная
- 12. Последствия включения в уравнение несущественной переменной 1.
- 13. Замещающие переменные Замещающая переменная – это переменная,
- 14. Замещающие переменные Пример: Время как замещающая переменная
- 15. Выбор переменных множественной регрессии Включение и исключение
- 16. Оценка значимости включаемой переменной Значимость включаемой переменной
- 17. Оценка значимости включаемой группы переменных Значимость включаемой
- 18. Оценка значимости включаемой группы переменных F-статистика может
- 19. Четыре критерия для включения переменной в уравнение
- 20. Процедуры поиска существенных переменных 1. Последовательный восходящий
- 21. Выбор переменных множественной регрессии Включение и исключение
- 22. Проверка наличия линейных ограничений Линейным ограничением называется
- 23. Выбор переменных множественной регрессии Включение и исключение
- 24. Тест ошибочной спецификации Рамсея Тест Рамсея позволяет
- 25. Тест ошибочной спецификации Амемии (Акаике) Выбирается уравнение
- 26. Выбор переменных регрессии: вложенные и невложенные модели
- 27. J-тест ошибочной спецификации Дэвидсона-МакКиннона для невложенных моделей
- 28. J-тест ошибочной спецификации Дэвидсона-МакКиннона для невложенных моделей
- 29. Конец лекции
Спецификация уравнения регрессии Выбор переменных Выбор формы зависимости (следующая лекция)
Слайд 3Цели лекции
1. Рассмотрение проблемы спецификации
переменных в уравнениях множественной
линейной регрессии
2. Изучить последствия
неправильного
выбора переменных
3. Найти средства, позволяющие улучшить
процедуру выбора переменных
выбора переменных
3. Найти средства, позволяющие улучшить
процедуру выбора переменных
Слайд 4Выбор переменных множественной регрессии
Включение и исключение переменных
1. Влияние на коэффициенты уравнения
2.
Влияние на значимость коэффициентов
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
Слайд 5Последствия не включения в уравнение существенной переменной
Переменная называется существенной,
если она должна
быть включена в
уравнение (согласно правильной теории)
уравнение (согласно правильной теории)
Будем также говорить об исключении переменной из правильно специфицированного уравнения регрессии
Слайд 6Последствия не включения в уравнение существенной переменной
1. Уменьшается возможность правильной оценки
и
интерпретации уравнения
2. Коэффициенты при оставшихся переменных
могут оказаться смещенными
3. Их стандартные ошибки, t-статистики и другие
показатели качества становятся некорректными и
не могут быть использованы для суждения о
качестве уравнения
2. Коэффициенты при оставшихся переменных
могут оказаться смещенными
3. Их стандартные ошибки, t-статистики и другие
показатели качества становятся некорректными и
не могут быть использованы для суждения о
качестве уравнения
Слайд 7Отсутствие существенной переменной
Если объясняющая переменная X2 отсутствует, то
где
Механизм разрушения оценок
Если объясняющие переменные коррелированы, то нарушается предпосылка 40 некоррелированности случайного члена и объясняющих переменных
Слайд 8Отсутствие существенной переменной
Оценка смещения коэффициента
Направление смешения зависит от знака истинного значения
коэффициента при отсутствующей переменной и ковариации объясняющих переменных
Слайд 9Отсутствие существенной переменной
Направление смещения коэффициента
1. Ковариация оценивается по выборке
2. Знак коэффициента
при отсутствующей переменной берется из экономической теории
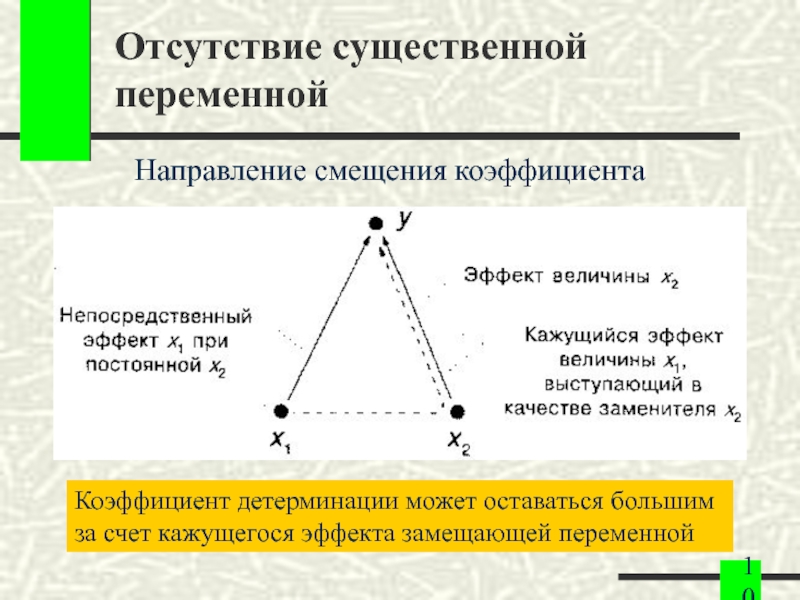
Слайд 10Отсутствие существенной переменной
Направление смещения коэффициента
Коэффициент детерминации может оставаться большим за счет
кажущегося эффекта замещающей переменной
Слайд 11Последствия включения в уравнение несущественной переменной
Переменная называется несущественной,
если она не должна
быть включена в
уравнение (согласно правильной теории)
уравнение (согласно правильной теории)
Будем также говорить о включении лишней переменной в правильное уравнение регрессии
Слайд 12Последствия включения в уравнение несущественной переменной
1. Не теряется возможность правильной оценки
и
интерпретации уравнения
2. Коэффициенты при существенных переменных
остаются несмещенными
3. Стандартные ошибки растут, t-статистики
уменьшаются, эффективность оценок падает
4. Несущественная переменная может быть
значимой, уравнение с ней – давать лучшую оценку
5. Увеличивается риск мультиколлинеарности
2. Коэффициенты при существенных переменных
остаются несмещенными
3. Стандартные ошибки растут, t-статистики
уменьшаются, эффективность оценок падает
4. Несущественная переменная может быть
значимой, уравнение с ней – давать лучшую оценку
5. Увеличивается риск мультиколлинеарности
Слайд 13Замещающие переменные
Замещающая переменная – это переменная, которая
коррелирует с отсутствующей переменной уравнения
регрессии,
и за счет этого выполняет функции этой
отсутствующей переменной
отсутствующей переменной
Часто бывает, что мы не можем найти данные по переменной, которую нужно включить в уравнение регрессии
Причины использования замещающей переменной:
1. В уравнении отсутствует существенная переменная со всеми вытекающими из этого последствиями.
2. Результаты оценки регрессии с включением замещающей переменной могут дать косвенную информацию об отсутствующей переменной
Слайд 14Замещающие переменные
Пример: Время как замещающая переменная для показателя
технического прогресса в производственной
функции Кобба-
Дугласа
Дугласа
Включение замещающей переменной позволяет правильно оценить роль других факторов, освободив их от функции замещения отсутствующей переменной
Коэффициенты замещающих переменных не имеют интерпретации, а сами замещающие факторы не могут быть использованы для формирования экономической политики
Слайд 15Выбор переменных множественной регрессии
Включение и исключение переменных
1. Влияние на коэффициенты уравнения
2.
Влияние на значимость коэффициентов
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
Слайд 16Оценка значимости включаемой переменной
Значимость включаемой переменной
оценивается t-статистикой коэффициента
Эквивалентность предполагает двухстороннюю альтернативу
для t-критерия
Эквивалентный метод – использование F-критерия
Слайд 17Оценка значимости включаемой группы переменных
Значимость включаемой группы
переменных оценивается F-тестом
Значимость группы переменных
не означает значимости каждой из переменных в этой группе
Слайд 18Оценка значимости включаемой группы переменных
F-статистика может быть найдена через
коэффициенты детерминации
Данный тест
может также использоваться для обратной процедуры: оценки значимости ухудшения качества модели при исключении из модели s переменных:
Слайд 19Четыре критерия для включения переменной в уравнение регрессии
1. Роль переменной в
уравнении опирается на
прочные теоретические основания
2. Высокое значение t-статистики коэффициента при
новой переменной
3. Скорректированный коэффициент детерминации
растет при включении переменной
4. Другие коэффициенты испытывают значительное
смещение при включении новой переменной
прочные теоретические основания
2. Высокое значение t-статистики коэффициента при
новой переменной
3. Скорректированный коэффициент детерминации
растет при включении переменной
4. Другие коэффициенты испытывают значительное
смещение при включении новой переменной
Слайд 20Процедуры поиска существенных переменных
1. Последовательный восходящий поиск
2. Последовательный нисходящий поиск
Обе процедуры
могут привести к серьезным ошибкам и следует избегать их автоматического применения, либо резко ограничивать объем поиска
Слайд 21Выбор переменных множественной регрессии
Включение и исключение переменных
1. Влияние на коэффициенты уравнения
2.
Влияние на значимость коэффициентов
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
Слайд 22Проверка наличия линейных ограничений
Линейным ограничением называется условие
линейной зависимости коэффициентов регрессии
Справедливость гипотезы
о наличии линейного ограничения позволяет исключить лишнюю переменную (m → m−1). Проверка проводится по F-критерию или по t-критерию (непосредственно для включаемой переменной)
Слайд 23Выбор переменных множественной регрессии
Включение и исключение переменных
1. Влияние на коэффициенты уравнения
2.
Влияние на значимость коэффициентов
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
регрессии и уравнения в целом
3. Линейные ограничения
4. Тесты ошибочной спецификации
Слайд 24Тест ошибочной спецификации Рамсея
Тест Рамсея позволяет проверить, стоит ли начинать поиск
дополнительной
переменной для включения в уравнение
1. Оценивается уравнение регрессии
2. Вычисляются степени зависимой переменной
3. Оценивается уравнение регрессии
4. Проводится оценка улучшения по F-критерию
Слайд 25Тест ошибочной спецификации Амемии (Акаике)
Выбирается уравнение с меньшим значением PC
Смысл теста
Амемии в том, что он позволяет
минимизировать среднюю ошибку оценки b
минимизировать среднюю ошибку оценки b
Является вариантом скорректированного коэффициента детерминации и превосходит его
Слайд 26Выбор переменных регрессии: вложенные и невложенные модели
Вложенные модели непосредственно сравнимы. Сравнение
невложенных
моделей возможно только с помощью
специальных процедур.
специальных процедур.
Вложенная модель является частным случаем (ограниченной версией) более общей модели.
Невложенные модели имеют разные наборы переменных.
Слайд 27J-тест ошибочной спецификации Дэвидсона-МакКиннона для невложенных моделей
1. Оценивается уравнение регрессии (A)
2.
Расчетные значения зависимой переменной из модели (A)
включаются в модель (B) в качестве дополнительной
объясняющей переменной
включаются в модель (B) в качестве дополнительной
объясняющей переменной
3. Проводится оценка улучшения модели по F-критерию
4. Делается симметричная процедура
Слайд 28J-тест ошибочной спецификации Дэвидсона-МакКиннона для невложенных моделей
В результате применения теста возможны
четыре случая:
1. Модель (A) значимо улучшается, а (B) – нет.
Вывод: выбираем модель (B).
2. Модель (B) значимо улучшается, а (A) – нет.
Вывод: выбираем модель (A).
3. Обе модели значимо улучшаются.
Вывод: ни одна из них не пригодна.
4. Обе модели улучшаются не значимо.
Вывод: данных недостаточно, чтобы различить качество
моделей.
1. Модель (A) значимо улучшается, а (B) – нет.
Вывод: выбираем модель (B).
2. Модель (B) значимо улучшается, а (A) – нет.
Вывод: выбираем модель (A).
3. Обе модели значимо улучшаются.
Вывод: ни одна из них не пригодна.
4. Обе модели улучшаются не значимо.
Вывод: данных недостаточно, чтобы различить качество
моделей.
