- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показательное распределение презентация
Содержание
- 1. Показательное распределение
- 2. Показательным (экспоненциальным) распределением СВ называют распределение СВ,
- 4. Найдем функцию распределения:
- 5. Обозначим y=λx, dy=d(λx). и проинтегрируем интеграл
- 6. Определим второй начальный момент:
- 7. Дисперсия и стандартное отклонение соответственно: D[X]=α2[X]–(M[X])2
- 8. §3.6.2.3. Нормальное распределение Нормальный закон распределения
- 9. Этот закон является предельным законом, к которому
- 10. Кривая нормального закона имеет вид:
- 11. Вычислим основные характеристики СВ Х. МО:
- 12. т.к. и -
- 13. Определим теперь дисперсию:
- 14. После всех преобразований получим D[X]=σ2 , поскольку
- 15. Т.к. изменение (х-mx) на обратный знак не
- 16. Увеличение или уменьшение σ2 ведет соответственно к
- 17.
- 18.
- 20. Правило трёх сигм. Если случайная величина
Слайд 2Показательным (экспоненциальным) распределением СВ называют распределение СВ, которое описывается плотностью распределения
р(х)=
где
λ-положительная постоянная величина.
Слайд 4Найдем функцию распределения:
Определим числовые характеристики распределения.
Вычислим МО по формуле:
M[X]=
Слайд 5Обозначим y=λx, dy=d(λx).
и проинтегрируем интеграл по частям, полагая u=y, du=dy,
а dv=exp(-y)dy, v=-exp(-y).
Тогда после всех преобразований получим: M[X]=1/λ.
Вычислим дисперсию
D[X]=α2[X]–(M[X])2
Слайд 6Определим второй начальный момент:
Введем обозначения y=λx, dy=d(λx)
и проинтегрируем интеграл по
частям, полагая u=y2, du=2ydy, а dv=exp(-y)dy, v=-exp(-y).
Тогда после всех преобразований получим α2[X]=2/λ2.
Тогда после всех преобразований получим α2[X]=2/λ2.
Слайд 7Дисперсия и стандартное отклонение соответственно:
D[X]=α2[X]–(M[X])2 =1/λ2;
σ=1/λ.
Показательный закон широко используется
в теории надежности при исследовании отказов и безотказной работы процессов и систем.
Слайд 8§3.6.2.3. Нормальное распределение
Нормальный закон распределения (закон Гаусса) наиболее часто встречающийся на
практике закон распределения, описывающий случайные возмущения и отклонения основных характеристик процессов и систем, ошибки измерений и т.д.
Слайд 9 Этот закон является предельным законом, к которому приближаются другие законы распределения
при весьма часто встречающихся типичных условиях.
Непрерывная СВ называется распределенной по нормальному закону, если ее плотность вероятности определяется выражением:
р(х)=
Непрерывная СВ называется распределенной по нормальному закону, если ее плотность вероятности определяется выражением:
р(х)=
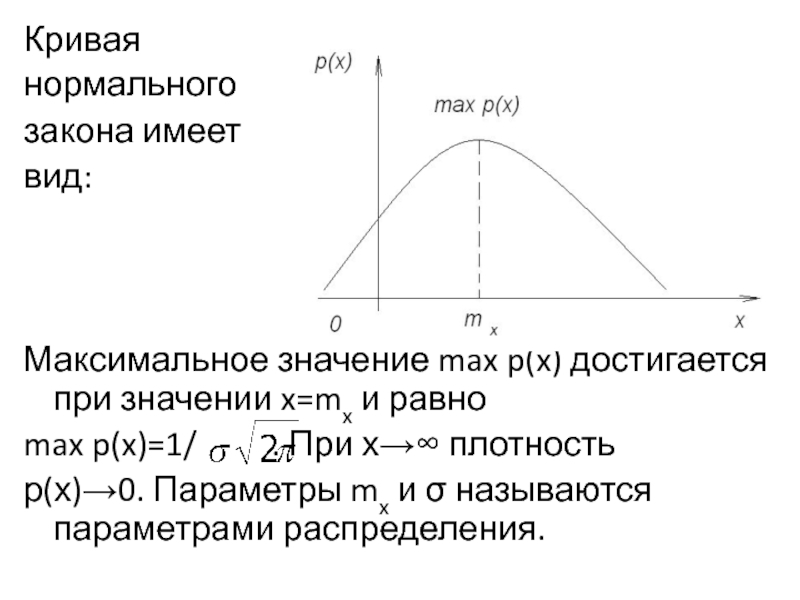
Слайд 10Кривая
нормального
закона имеет
вид:
Максимальное значение max p(x) достигается при значении x=mx и
равно
max p(x)=1/ . При х→∞ плотность
р(х)→0. Параметры mx и σ называются параметрами распределения.
max p(x)=1/ . При х→∞ плотность
р(х)→0. Параметры mx и σ называются параметрами распределения.
Слайд 13Определим теперь дисперсию:
Заменим переменную и
применим интегрирование по частям (u=t, dv=2texp(-t2)dt,
du=dt, v=-exp(-t2))
Слайд 14После всех преобразований получим D[X]=σ2 , поскольку -exp(-t2) при t→±∞ убывает
быстрее, чем возрастает t.
Рассмотрим влияние параметров нормального распределения на форму кривой распределения.
Из выражения для плотности вероятности нормального распределения следует, что mx является центром симметрии и рассеивания,
Рассмотрим влияние параметров нормального распределения на форму кривой распределения.
Из выражения для плотности вероятности нормального распределения следует, что mx является центром симметрии и рассеивания,
Слайд 15Т.к. изменение (х-mx) на обратный знак не влияет на кривую распределения.
Увеличение или уменьшение mx ведет к смещению кривой распределения
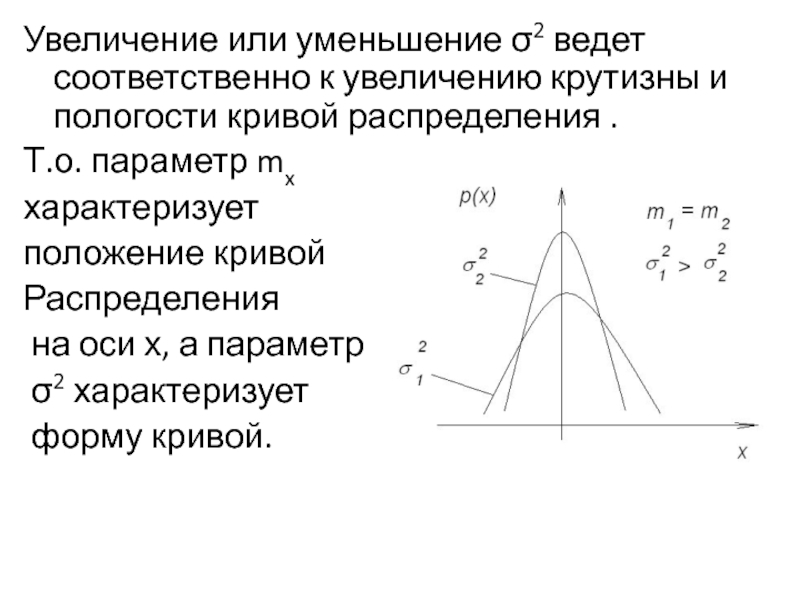
Слайд 16Увеличение или уменьшение σ2 ведет соответственно к увеличению крутизны и пологости
кривой распределения .
Т.о. параметр mx
характеризует
положение кривой
Распределения
на оси х, а параметр
σ2 характеризует
форму кривой.
Т.о. параметр mx
характеризует
положение кривой
Распределения
на оси х, а параметр
σ2 характеризует
форму кривой.
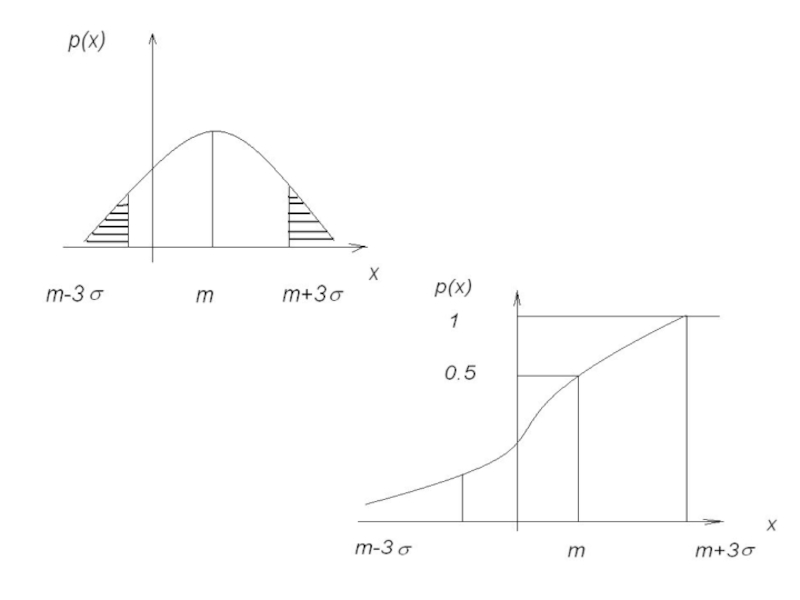
Слайд 20 Правило трёх сигм.
Если случайная величина распределена нормально, то абсолютная величина
её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения с вероятностью 0,9973.
Если закон распределения СВ неизвестен, а известны только m и σ, на практике обычно считают отрезок m±3σ, участком практически возможных значений СВ.
Если закон распределения СВ неизвестен, а известны только m и σ, на практике обычно считают отрезок m±3σ, участком практически возможных значений СВ.



![Найдем функцию распределения: Определим числовые характеристики распределения. Вычислим МО по формуле: M[X]=](/img/tmb/4/344287/b1b7372ae5b4fdaa91f08a6b45e019c7-800x.jpg)


![Дисперсия и стандартное отклонение соответственно: D[X]=α2[X]–(M[X])2 =1/λ2; σ=1/λ.Показательный закон широко используется в теории надежности при](/img/tmb/4/344287/138998ab185f0439e32c2179356f1af4-800x.jpg)



![т.к. и - интеграл Эйлера-Пуассона. Т.о. M[X]= mx .](/img/tmb/4/344287/058f407a74e1ff0a1121b261dbe70de8-800x.jpg)

![После всех преобразований получим D[X]=σ2 , поскольку -exp(-t2) при t→±∞ убывает быстрее, чем возрастает t.](/img/tmb/4/344287/cb71d754b177f160316e02d927028262-800x.jpg)