Случайные события. (Лекция 2) презентация

Содержание

1. Классификация событий

Слайд 1Случайные события
1. Классификация.
2. Алгебра событий.

Слайд 21. Классификация событий

Слайд 309/22/2019
Ирина Юрьевна Харламова
Классификация событий
Случайным событием называется такой исход эксперимента или наблюдения,

который при реализации данного комплекса условий может произойти, а может и не произойти.


A, B, C…

Слайд 409/22/2019
Ирина Юрьевна Харламова
Классификация событий

Достоверным событием называется такое событие, которое при

реализации данного комплекса условий непременно произойдет.

U

Слайд 509/22/2019
Ирина Юрьевна Харламова
Классификация событий

Невозможным событием называется такое событие, которое заведомо не

может произойти при реализации данного комплекса условий.

V

Слайд 609/22/2019
Ирина Юрьевна Харламова
Классификация событий
События А и В называются несовместными, если в

результате данного испытания появление одного из них исключает появление второго.

Слайд 709/22/2019
Ирина Юрьевна Харламова
Классификация событий
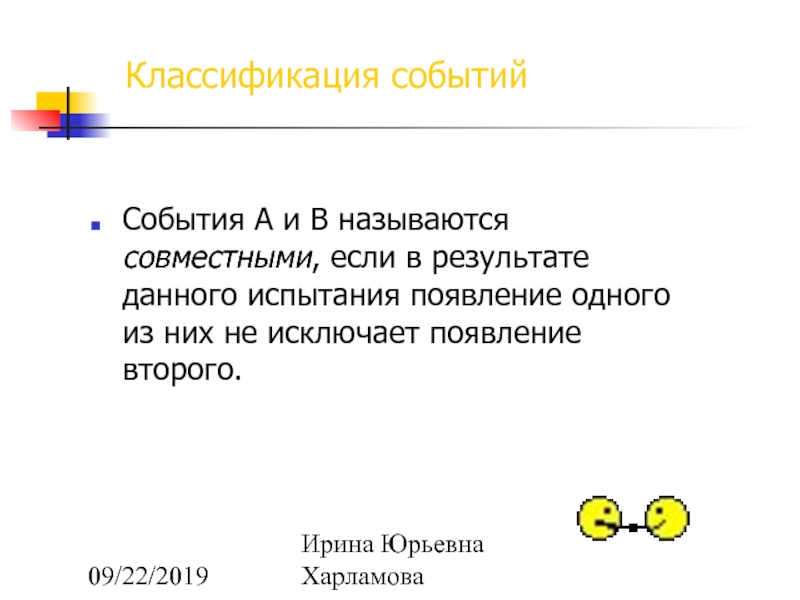
События А и В называются совместными, если в

результате данного испытания появление одного из них не исключает появление второго.

Слайд 809/22/2019
Ирина Юрьевна Харламова
Классификация событий

Два события А и А называются противоположными, если

не появление одного из них влечет появление другого.

Слайд 909/22/2019
Ирина Юрьевна Харламова
Классификация событий
Два события называются независимыми, если осуществление одного не

влияет на возможность осуществления другого.

Слайд 1009/22/2019
Ирина Юрьевна Харламова
Классификация событий
Два события называются зависимыми, если осуществление одного влияет

на возможность осуществления другого.

Слайд 1109/22/2019
Ирина Юрьевна Харламова
Классификация событий
Пусть производится один выстрел по мишени

Слайд 1209/22/2019
Ирина Юрьевна Харламова
Классификация событий

Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

Слайд 1309/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

В и С,
А6 и F,
А3 и В

несовместные

Слайд 1409/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

А8 и В,
А3 и С,
А2 и F,
А5 и H

совместные

Слайд 1509/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

В и С,
D и F

противоположные

Слайд 1609/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

G

невозможное

Слайд 1709/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

H

достоверное

Слайд 1809/22/2019
Ирина Юрьевна Харламова
Классификация событий
Событие А называется благоприятствующим событию В, если появление

события А влечет за собой появление события В.

А⇒В или А⊂В

Слайд 1909/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

Слайд 2009/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

Слайд 2109/22/2019
Ирина Юрьевна Харламова
Классификация событий
События А и В называются равносильными, если появление

события А влечет за собой появление события В и в то же время появление события В влечет за собой появление события А.

А⇔В или А=В

Слайд 2209/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

Слайд 2309/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

1. А0, А1, A2, A3, A4, A5, A6, A7, A8, A9, A10
2. В и С;
3. D и F.

Слайд 2409/22/2019
Ирина Юрьевна Харламова
Классификация событий
Если группа событий такова, что в результате испытания

обязательно должно произойти хотя бы одно из них, то эта группа событий называется полной группой событий.

Слайд 2509/22/2019
Ирина Юрьевна Харламова
Классификация событий
Ai — "выбито i очков, где i изменяется

от 0 до 10",
В — "выбито четное число очков",
С — "выбито нечетное число очков",
D — "выбито более 4 очков",
F — "выбито менее 5 очков",
G —"число выбитых очков больше 11",
H — "число выбитых очков меньше 12",
I — "выбито не менее 5 очков".

1. А0, А1, A2, A3, A4, A5, A6, A7, A8, A9, A10
2. В и С;
3. D и F.

Слайд 2609/22/2019
Ирина Юрьевна Харламова
Классификация событий
Каждое событие из полной группы попарно несовместных событий

будем называть исходом данного опыта (испытания). Часто исходы испытания называются элементарными событиями.

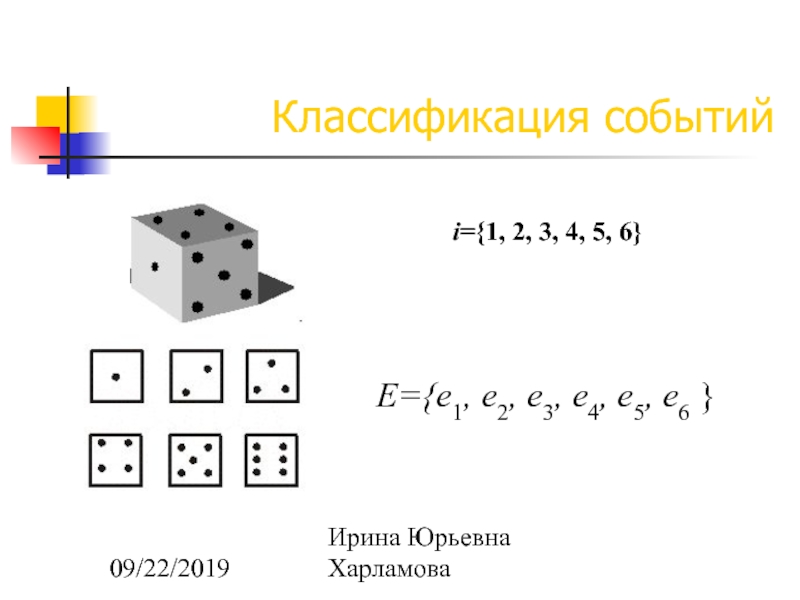
Множество всех возможных элементарных событий данного опыта называется пространством элементарных событий Е, а сами элементарные события еi — точками этого пространства.

Слайд 2709/22/2019
Ирина Юрьевна Харламова
i={1, 2, 3, 4, 5, 6}
Классификация событий
E={е1, е2, е3,

е4, е5, е6 }

Слайд 2809/22/2019
Ирина Юрьевна Харламова
Случайные события


E={е11, е12,.., е66 }

Слайд 2909/22/2019
Ирина Юрьевна Харламова
Случайные события



Слайд 3009/22/2019
Ирина Юрьевна Харламова
Классификация событий
События называются равновозможными, если по условию испытания нет

основания считать какое либо из них более возможным, чем другое.

Слайд 312. Алгебра случайных событий

Слайд 3209/22/2019
Ирина Юрьевна Харламова
Алгебра событий
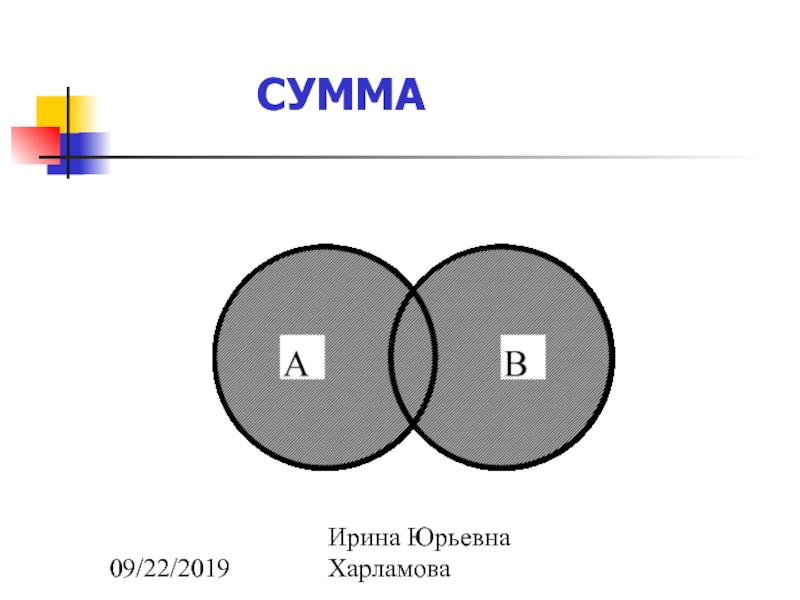
Суммой (объединением) двух событий А и В называется

третье событие С, состоящее в появлении или события А, или события В, или обоих этих событий.



Слайд 3309/22/2019
Ирина Юрьевна Харламова
Алгебра событий


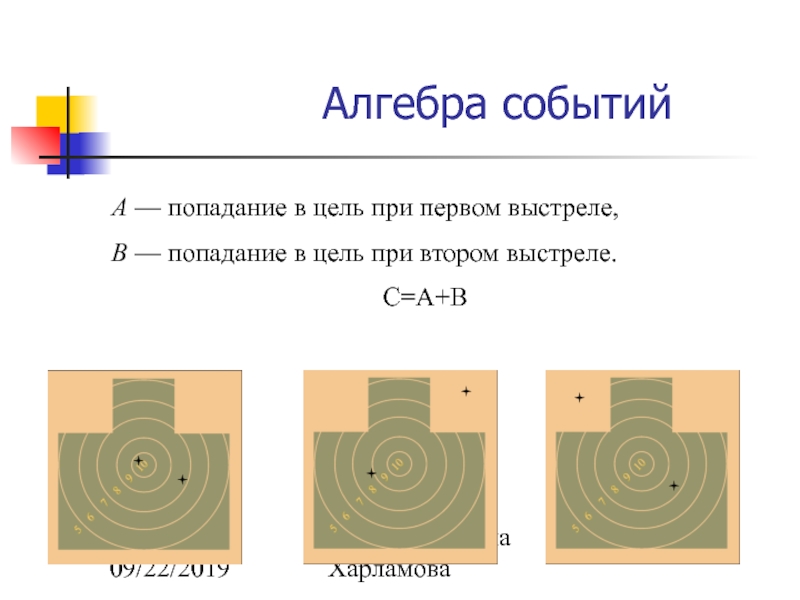
А — попадание в цель при первом выстреле,
В — попадание в

цель при втором выстреле.
С=A+B





Слайд 3409/22/2019
Ирина Юрьевна Харламова
Алгебра событий
Суммой (объединением) нескольких событий А1, А2 ,..., Аn

называется событие
А=А1+ А2+...+Аn,
состоящее в появлении хотя бы одного из этих событий.



Слайд 3509/22/2019
Ирина Юрьевна Харламова
СУММА


Слайд 3609/22/2019
Ирина Юрьевна Харламова
Алгебра событий
Произведением (пересечением) двух событий А и В называется

такое третье событие С, которое состоит в совместном появлении и события А, и события В.



Слайд 3709/22/2019
Ирина Юрьевна Харламова
Алгебра событий


А — попадание в цель при первом выстреле,
В — попадание в

цель при втором выстреле.
С=A·B

Слайд 3809/22/2019
Ирина Юрьевна Харламова
Алгебра событий
Произведением (объединением) нескольких событий А1, А2 ,..., Аn

называется событие
А=А1· А2·...·Аn,
состоящее в состоящее в совместном появлении всех этих событий.



Слайд 3909/22/2019
Ирина Юрьевна Харламова
ПРОИЗВЕДЕНИЕ




Слайд 4009/22/2019
Ирина Юрьевна Харламова
Алгебра событий
Если события А1 и А2 — несовместные события,

то их произведение — невозможное событие.




Слайд 4109/22/2019
Ирина Юрьевна Харламова
Алгебра событий
1. Произведение противоположных событий — невозможное событие:




2. Сумма противоположных

событий — достоверное событие. :


Слайд 42Спасибо за внимание!

Похожие презентации

Построение сечений многогранников 234
igra po matem 229
sravnenie grupp predmetov 236
Таблица умножения на 2 296
Методология научных исследований. Планирование экспериментов 506
Неевклидовы геометрии 400

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика