- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Скалярное произведение векторов. Разложение вектора по двум не коллинеарным векторам презентация
Содержание
- 1. Скалярное произведение векторов. Разложение вектора по двум не коллинеарным векторам
- 2. Дано: АВСD – параллелограмм
- 3. Угол между векторами.
- 4. Скалярное произведение векторов. Скалярным произведением двух
- 5. Если
- 6. Теорема: Любой вектор можно разложить по
- 7. x y 0 i j
- 8. x y 0 i j
- 9. 10. Каждая координата суммы двух или более
Дано: АВСD – параллелограмм Найти: 1) векторы, коллинеарные вектору ОС; 2) векторы, сонаправленные вектору АВ; 3) векторы, противоположно направленные вектору ВС; 4) векторы, равные вектору ВО; 5)
Слайд 2
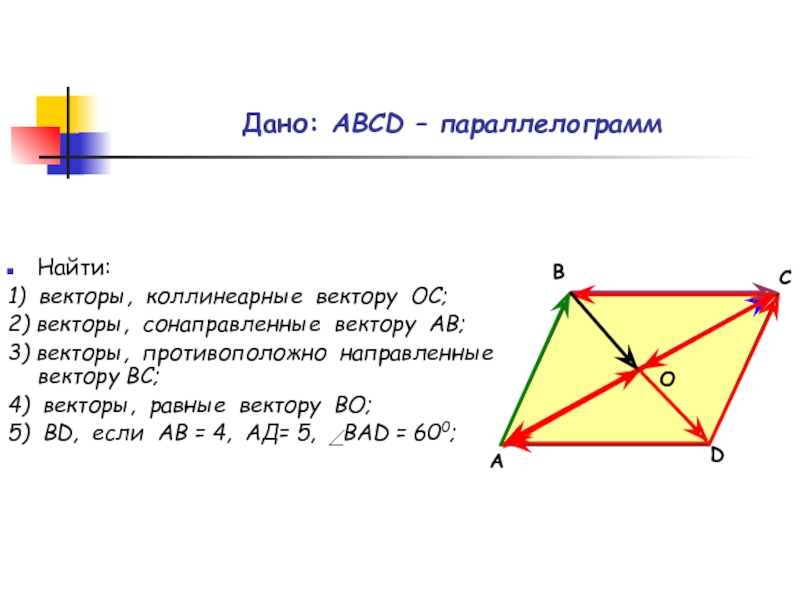
Дано: АВСD – параллелограмм
Найти:
1) векторы, коллинеарные вектору ОС;
2) векторы, сонаправленные
вектору АВ;
3) векторы, противоположно направленные вектору ВС;
4) векторы, равные вектору ВО;
5) ВD, если АВ = 4, АД= 5, ВАD = 600;
3) векторы, противоположно направленные вектору ВС;
4) векторы, равные вектору ВО;
5) ВD, если АВ = 4, АД= 5, ВАD = 600;
А
С
В
D
О
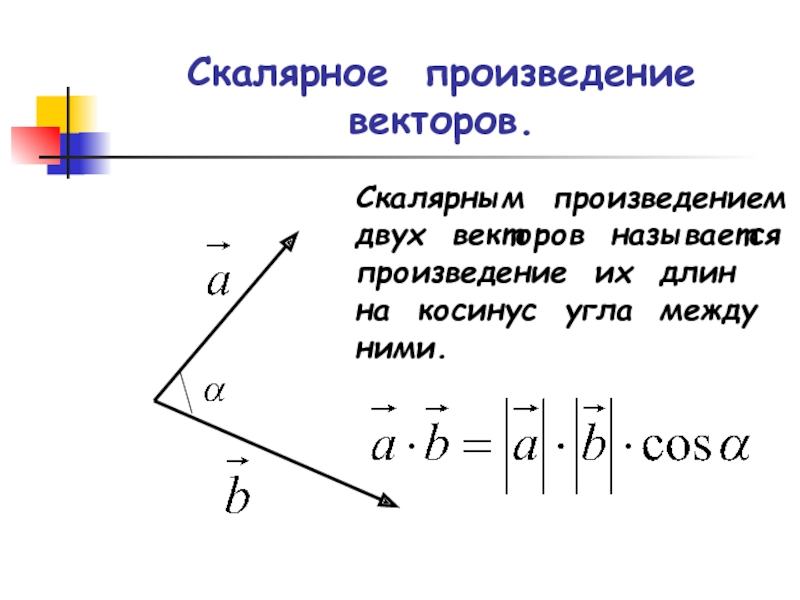
Слайд 4Скалярное произведение векторов.
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла
между
ними.
ними.
Слайд 5
Если , то
Если
, то
Если
,
то
Если
, то
Скалярное произведение
называется
скалярным квадратом вектора
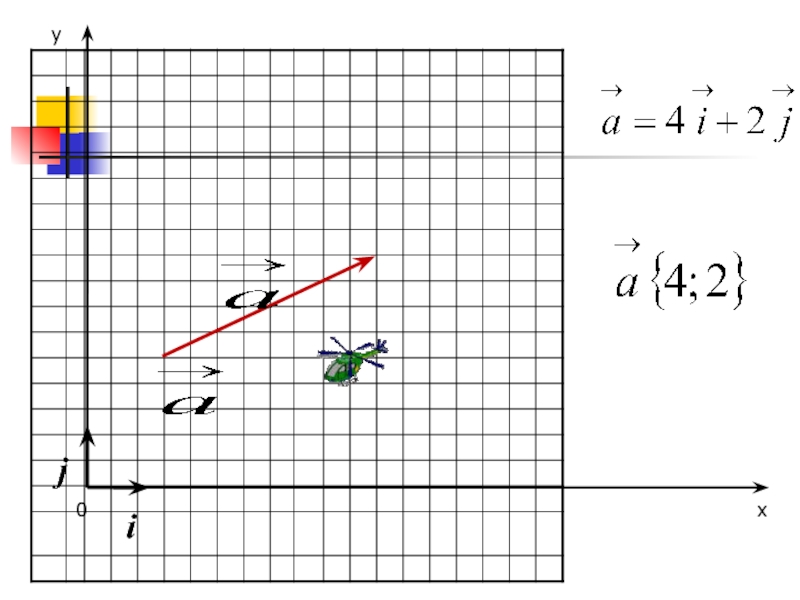
Слайд 6Теорема: Любой вектор можно разложить по двум данным неколлинеарным векторам,
причём коэффициенты разложения определяются единственным образом.
Слайд 910. Каждая координата суммы двух или более векторов равна сумме соответствующих
координат этих векторов. а+b=(х1+х2)i + (у1+у2)j
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. а-b=(х1-х2)i + (у1-у2)j
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. ка =кхi +куj
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. а-b=(х1-х2)i + (у1-у2)j
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. ка =кхi +куj
