- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки существования предела презентация
Содержание
Слайд 16.7. ПРИЗНАКИ СУЩЕСТВОВАНИЯ
ПРЕДЕЛА
Теорема 1.
Если числовая последовательность
монотонна и ограничена, то она
имеет предел.
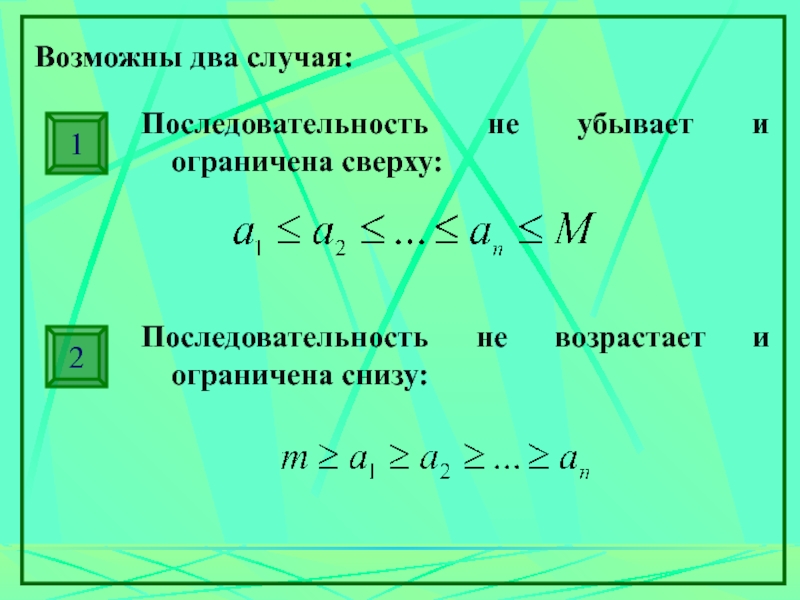
Слайд 2Возможны два случая:
Последовательность не убывает и ограничена сверху:
1
Последовательность не возрастает и
ограничена снизу:
2
Слайд 3Теорема 2.
Если в некоторой окрестности точки
х0 (или при достаточно больших
значениях х) функция f(x) заключена
между двумя функциями φ(х) и ψ(х),
имеющими одинаковый предел,
равный А, то функция f(x) имеет
тот же предел А.
Слайд 4Доказательство:
Пусть при
существуют пределы
Следовательно, для любого, сколь угодно малого числа ε>0,
найдется такое положительное число δ, что при всех х, таких что |x-x0|<δ, одновременно выполняются неравенства:
Слайд 5или
Т.к. по условию функция f(x) заключена между функциями φ(х) и ψ(х),
то
Т.е.
А это и означает по определению предела функции в точке, что