- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Обходы графов презентация
Содержание
- 1. Обходы графов
- 2. Существует ряд задач на графах, в которых
- 3. 3.1. Эйлеровы цепи и циклы
- 4. Определение. Эйлеровой цепью (циклом) называется цепь (цикл),
- 5. Теорема. Эйлерова цепь (цикл) существует тогда
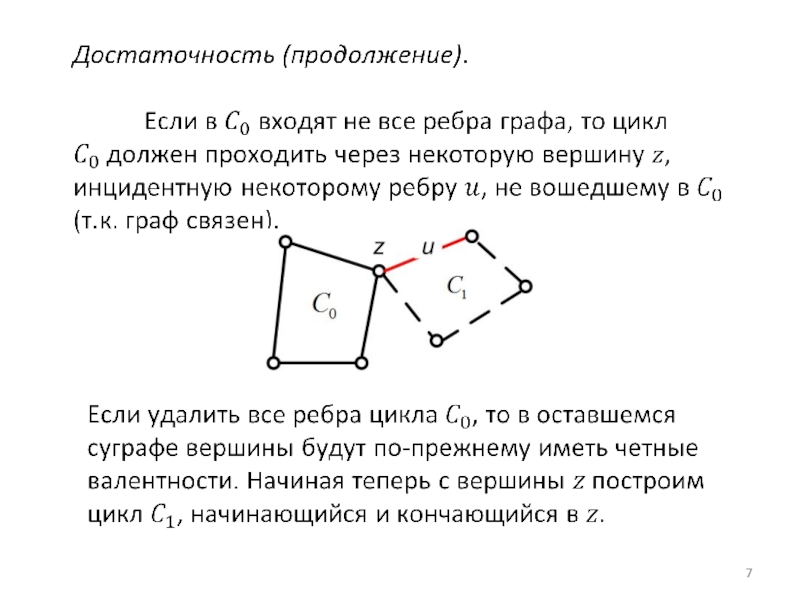
- 6.
- 7.
- 8.
- 9. На этом доказательстве основан алгоритм нахождения эйлеровой цепи.
- 10. Алгоритм
- 11.
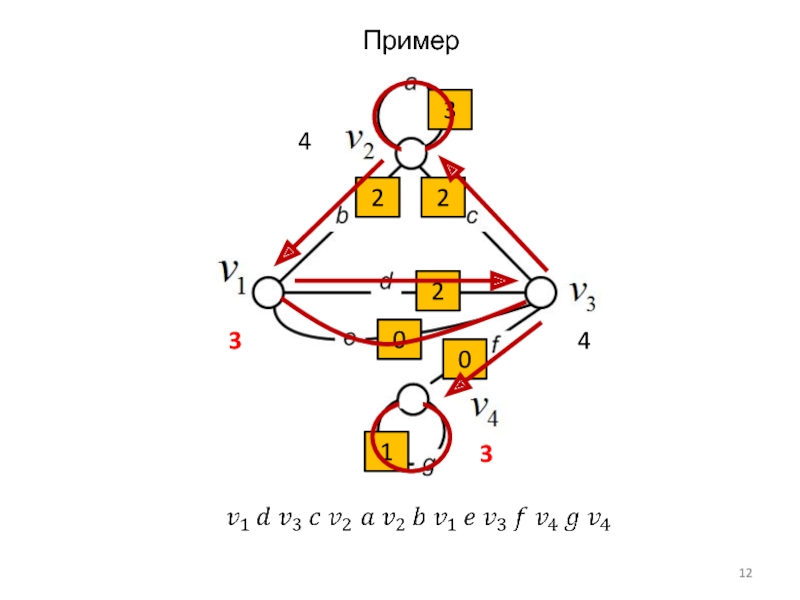
- 12. 4 3 4 3 0 0 1 2 2 3 2 Пример
- 13. Задача китайского почтальона В графе с неотрицательными
- 14. 3.1. Гамильтоновы цепи и циклы
- 15. Постановка задачи Определение. Гамильтоновой цепью (циклом) графа
- 16. Граф Гамильтона Додекаэдр: 12 граней, 20
- 17. Мы рассмотрим два простейших переборных алгоритма
- 18. Поиск в ширину 2
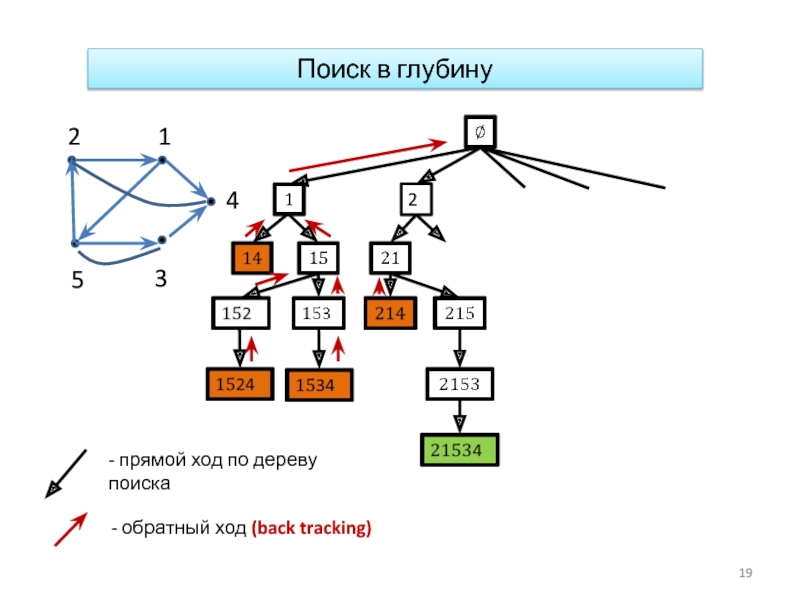
- 19. Поиск в глубину 2
- 20. Задача коммивояжера Задача коммивояжера (travelling seller problem,
- 21.
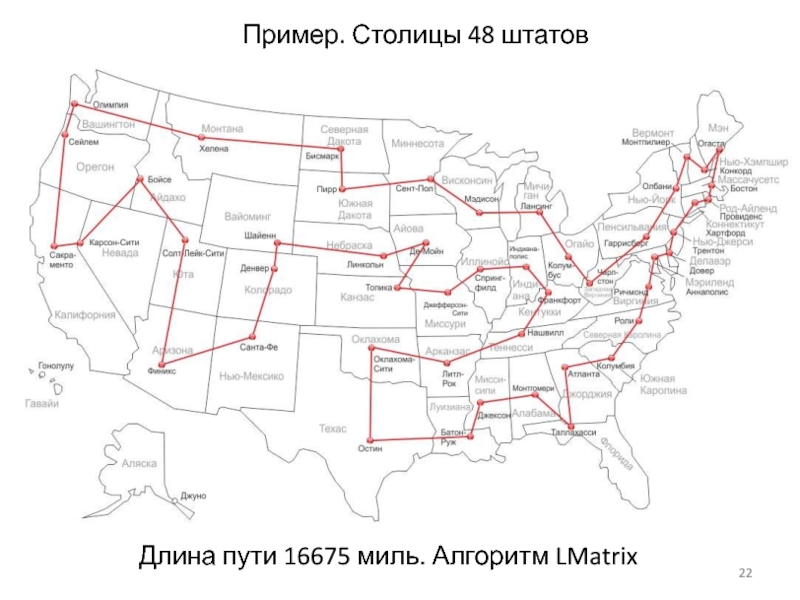
- 22. Пример. Столицы 48 штатов Длина пути 16675 миль. Алгоритм LMatrix
Слайд 2Существует ряд задач на графах, в которых требуется найти маршрут, который
Часто требуется, чтобы длина этого маршрута была минимальной (для взвешенных графов), или ограничивается число проходов по одному и тому же элементу графа.
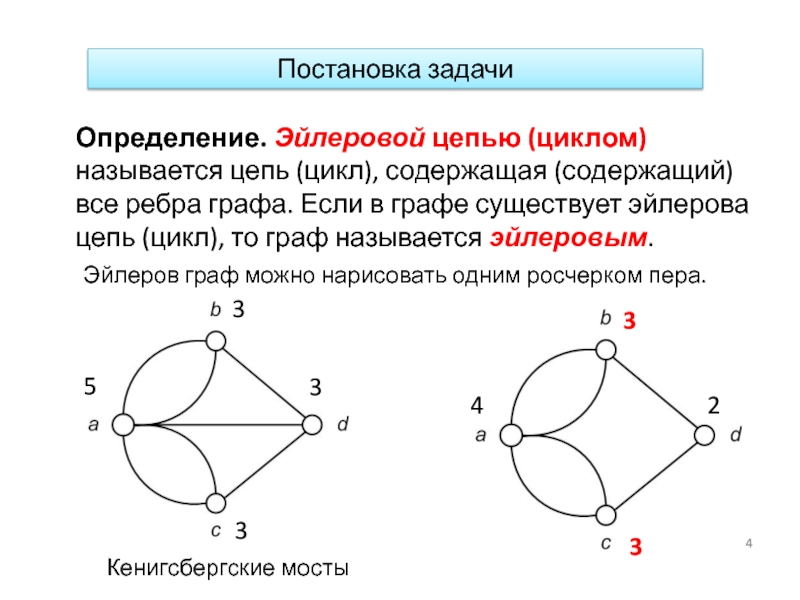
Слайд 4Определение. Эйлеровой цепью (циклом) называется цепь (цикл), содержащая (содержащий) все ребра
Эйлеров граф можно нарисовать одним росчерком пера.
5
3
3
3
3
3
4
2
Постановка задачи
Кенигсбергские мосты
Слайд 5
Теорема. Эйлерова цепь (цикл) существует тогда и только тогда, когда число
Теорема Эйлера (1736 г.)
Слайд 13Задача китайского почтальона
В графе с неотрицательными весами ребер найти циклический маршрут
Почтальон называется китайским потому, что первоначально эту задачу изучал китайский математик Мэй-Ку Куан в 1962 году.
Очевидно, если граф эйлеров, то эйлеров цикл и будет оптимальным. Если граф не эйлеров, то задача становится весьма трудоемкой. Для ее решения имеются специальные алгоритмы, сокращающие число перебираемых вариантов.
Слайд 15Постановка задачи
Определение. Гамильтоновой цепью (циклом) графа называется простая цепь (простой цикл),
Сэр Уильям Роуэн Гамильтон
(1805-1865) – самый известный ирландский математик, один из лучших математиков 19 века. Известен фунда-ментальными открытиями в математике , механике , физике (векторный анализ, вариационное исчисление, общий прин-цип наименьшего действия в механике, теория распространения света и др.)
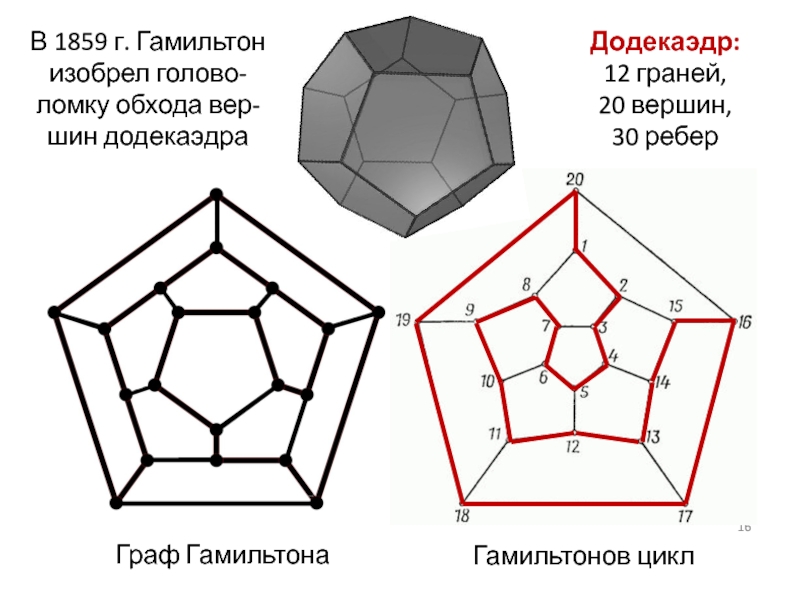
Слайд 16Граф Гамильтона
Додекаэдр:
12 граней,
20 вершин,
30 ребер
Гамильтонов цикл
В 1859 г. Гамильтон изобрел
Слайд 17
Мы рассмотрим два простейших переборных алгоритма поиска гамильтоновой цепи (цикла), пригодных
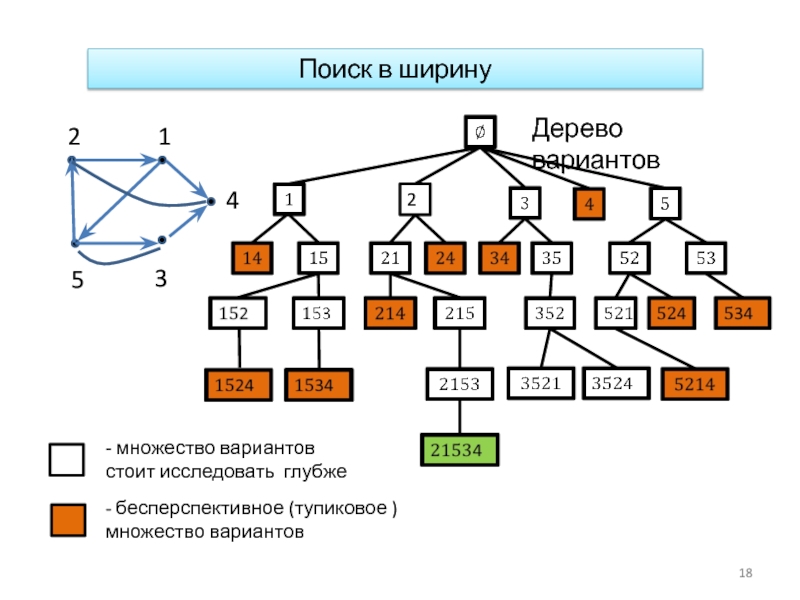
Слайд 18Поиск в ширину
2
- бесперспективное (тупиковое ) множество вариантов
- множество вариантов
стоит исследовать
Дерево вариантов
Слайд 20Задача коммивояжера
Задача коммивояжера (travelling seller problem, TSP) формулируется следующим образом: во
общее пройденное расстояние было минимальным?