- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признаки параллельности двух прямых презентация
Содержание
- 1. Признаки параллельности двух прямых
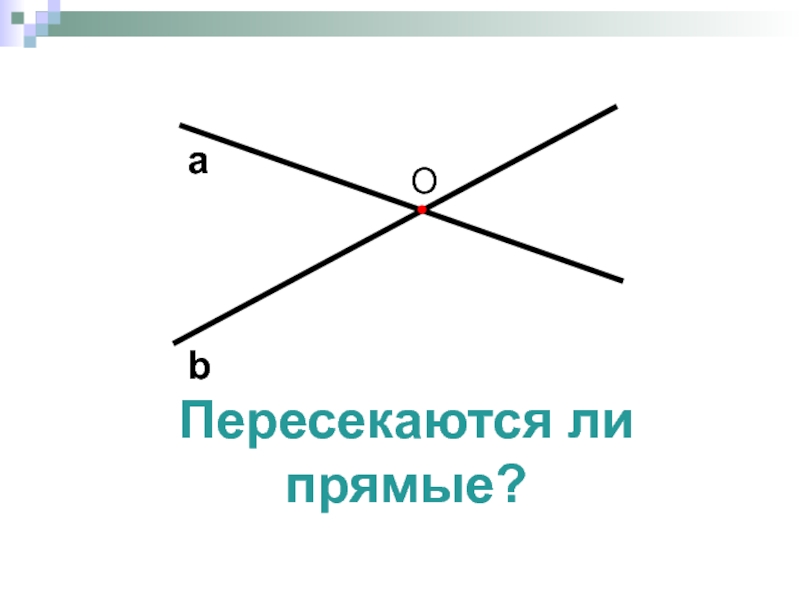
- 2. Пересекаются ли прямые?
- 3. Пересекаются ли прямые? а b
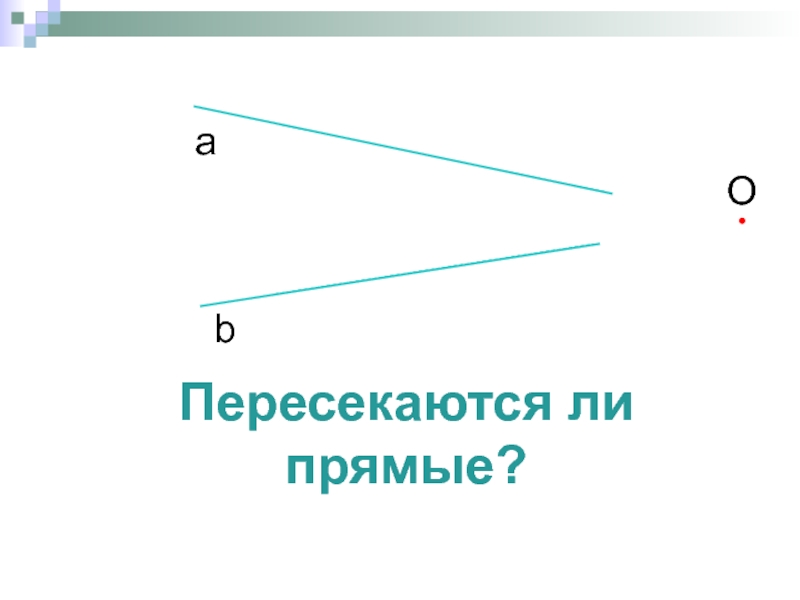
- 4. Пересекаются ли прямые? а b
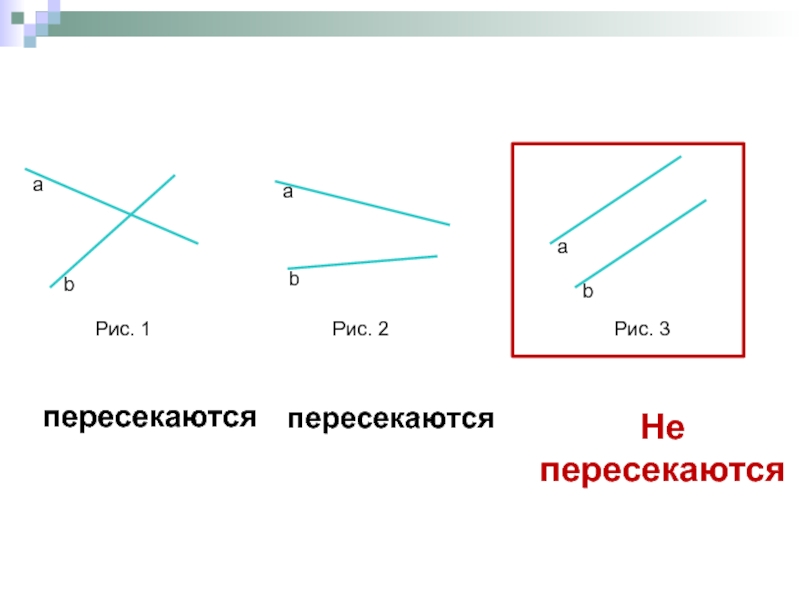
- 5. пересекаются Рис. 3 пересекаются Не пересекаются
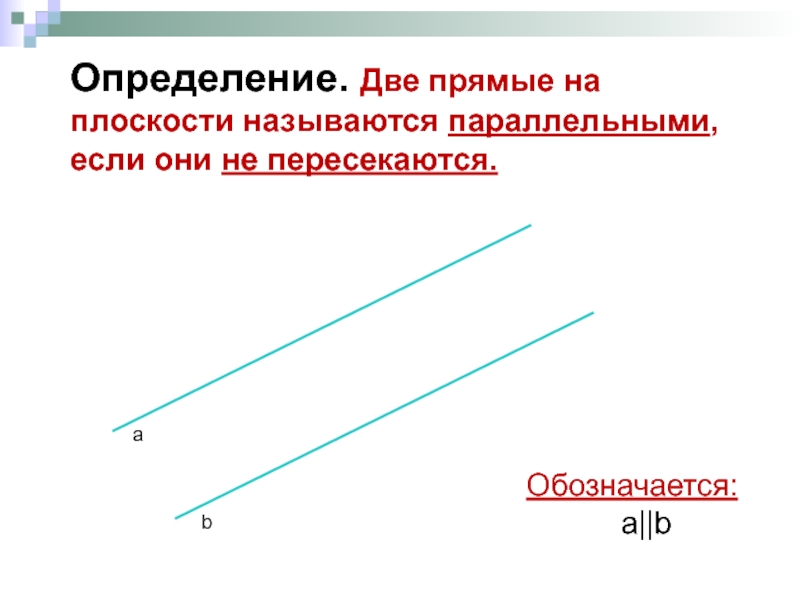
- 6. Определение. Две прямые на плоскости называются параллельными,
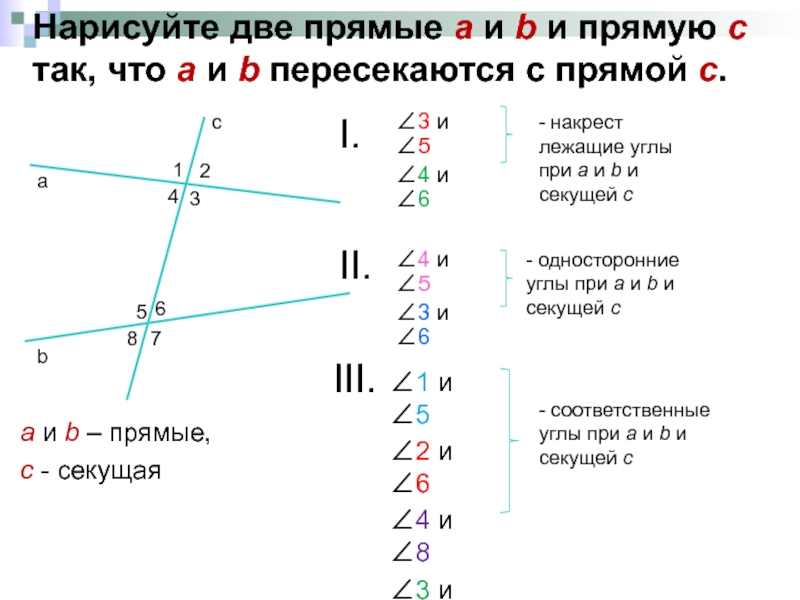
- 7. Нарисуйте две прямые а и b и
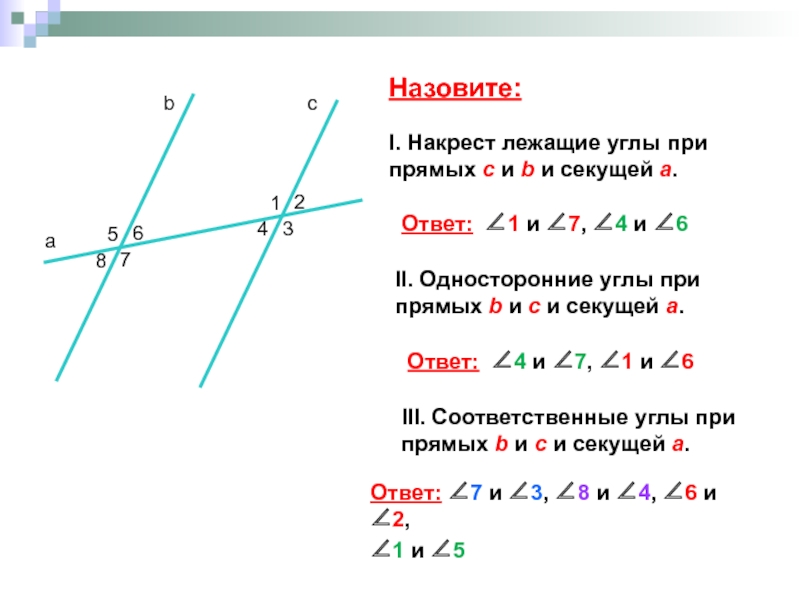
- 8. Назовите: I. Накрест лежащие углы
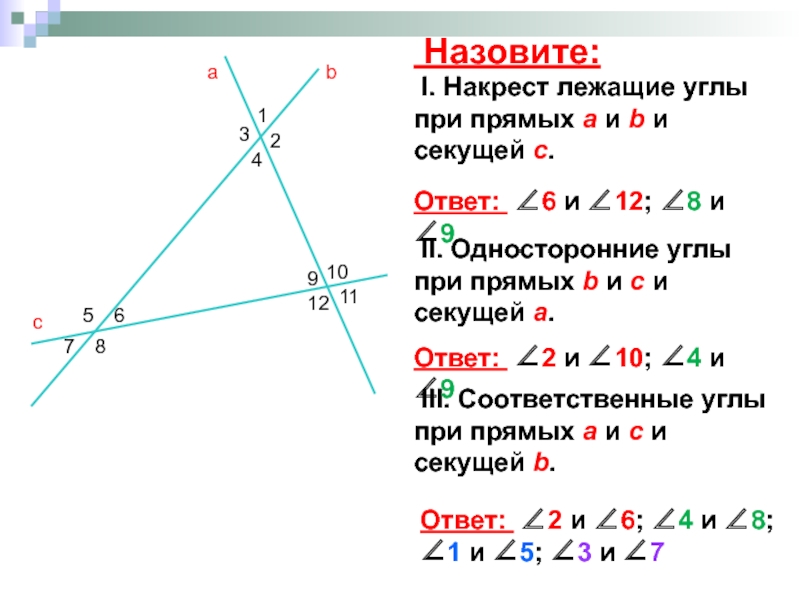
- 9. Назовите: а b c 1 2
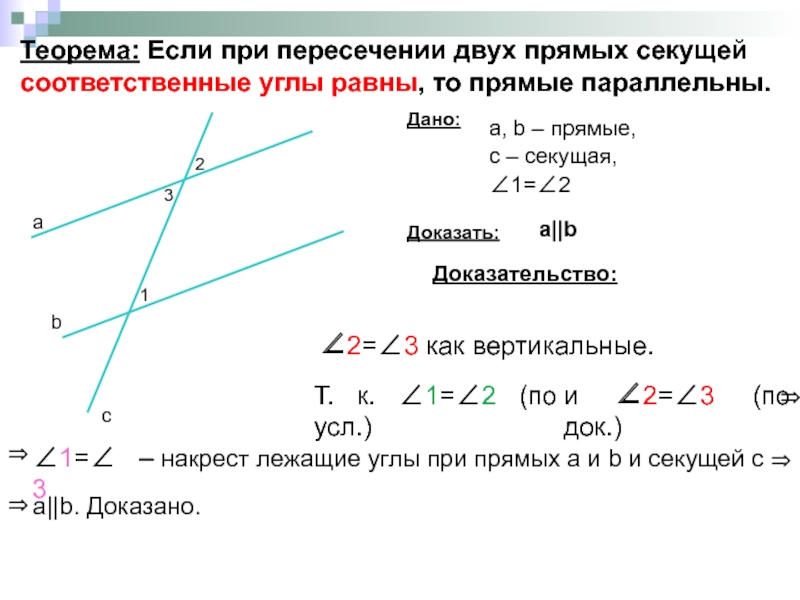
- 10. Теорема: Если при пересечении двух прямых секущей
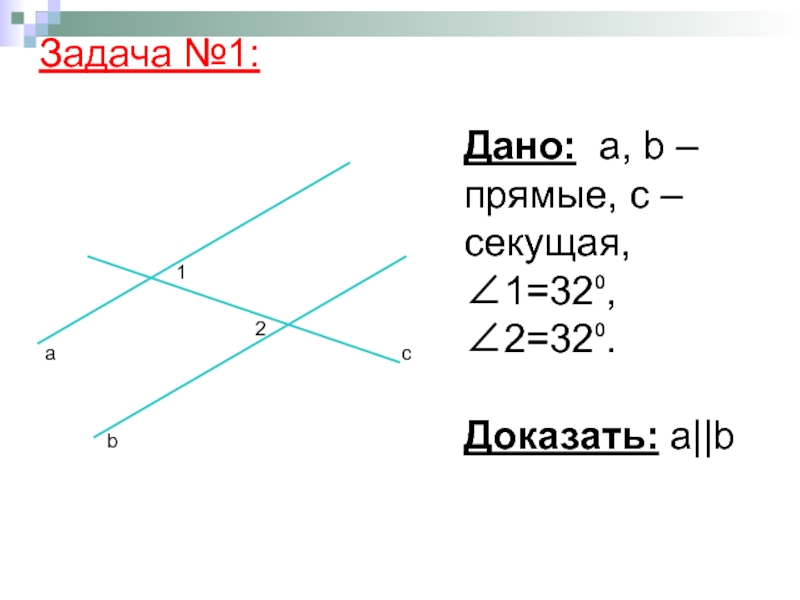
- 11. Дано: а, b – прямые, с – секущая, ∠1=32⁰, ∠2=32⁰. Доказать: а||b Задача №1:
- 12. Теорема: Если при пересечении двух прямых секущей
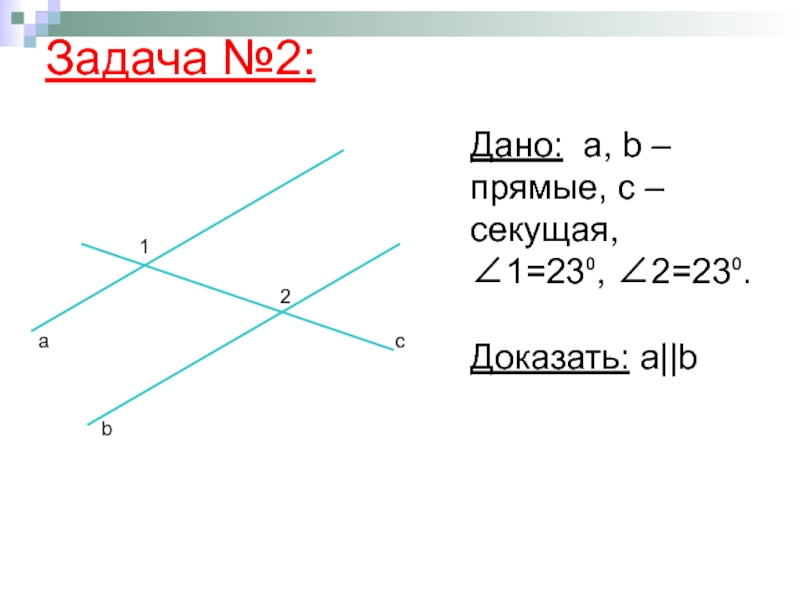
- 13. Задача №2: Дано: а, b –
- 14. Теорема: Если при пересечении двух прямых секущей
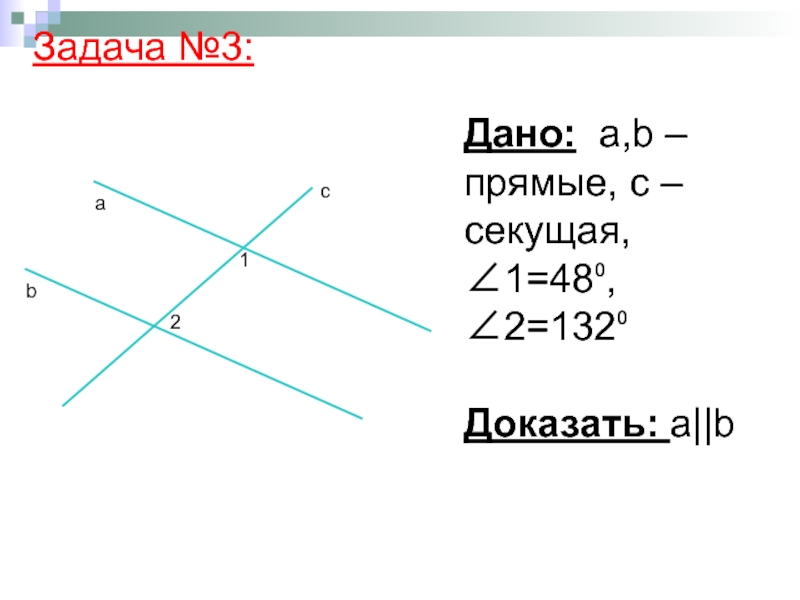
- 15. Дано: а,b – прямые, с – секущая, ∠1=48⁰, ∠2=132⁰ Доказать: а||b Задача №3:
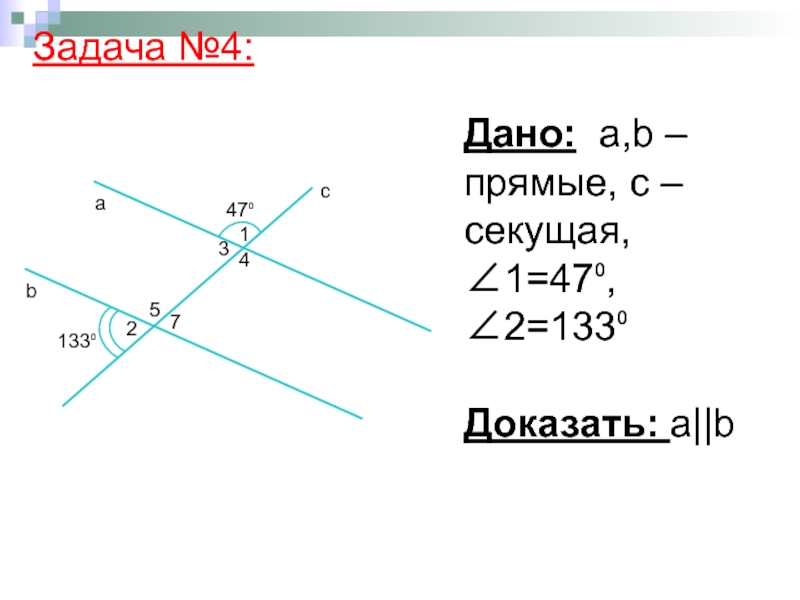
- 16. Дано: а,b – прямые, с – секущая,
- 17. Классная работа: № 186(в) Домашняя работа: п.п. 24, 25, № 186(а, б)
Слайд 6Определение. Две прямые на плоскости называются параллельными, если они не пересекаются.
Обозначается:
Слайд 7Нарисуйте две прямые а и b и прямую с так, что
а и b – прямые,
с - секущая
1
2
4
3
5
6
7
8
Слайд 8Назовите: I. Накрест лежащие углы при прямых с и b и
Ответ: ∠1 и ∠7, ∠4 и ∠6
а
b
с
1
2
3
4
5
6
7
8
II. Односторонние углы при прямых b и с и секущей а.
Ответ: ∠4 и ∠7, ∠1 и ∠6
III. Соответственные углы при прямых b и с и секущей а.
Ответ: ∠7 и ∠3, ∠8 и ∠4, ∠6 и ∠2,
∠1 и ∠5
Слайд 9 Назовите:
а
b
c
1
2
3
4
5
6
8
7
10
11
12
9
I. Накрест лежащие углы при прямых а и b
II. Односторонние углы при прямых b и с и секущей а.
III. Соответственные углы при прямых а и с и секущей b.
Ответ: ∠6 и ∠12; ∠8 и ∠9
Ответ: ∠2 и ∠10; ∠4 и ∠9
Ответ: ∠2 и ∠6; ∠4 и ∠8;
∠1 и ∠5; ∠3 и ∠7
Слайд 10Теорема: Если при пересечении двух прямых секущей накрест лежащие углы равны,
Дано:
а
b
с
а, b – прямые,
с – секущая,
∠1=∠2
1
2
Доказать:
а||b
Доказательство:
I случай: ∠1=∠2=90⁰⇒а⊥с
II случай: Ч/з точку О – сер. АВ проведем ОН⊥а.
А
В
О
Н
и b⊥с⇒а||b
Н1
На b отложим ВН1=АН.
∆ОНА и ∆ОН1В
1. ∠1=∠2 ( по усл)
2. ОВ=ОА ( по постр)
3. АН=ВН1 ( по постр)
⇒∆ОНА и ∆ОН1В по I призн.
⇒∠3=∠4 и ∠5=∠6.
Из ∠3=∠4 ⇒точки Н, О, Н1 лежат на одной прямой
Из ∠5=∠6=90⁰⇒а⊥НН1 и b⊥НН1⇒a||b. Доказано.
3
4
5
6
Слайд 12Теорема: Если при пересечении двух прямых секущей соответственные углы равны, то
Дано:
а
b
с
а, b – прямые,
с – секущая,
∠1=∠2
3
1
Доказать:
а||b
Доказательство:
2
∠2=∠3 как вертикальные.
Т. к. ∠1=∠2 (по усл.)
и ∠2=∠3 (по док.)
∠1=∠3
⇒
– накрест лежащие углы при прямых а и b и секущей с
⇒
а||b. Доказано.
⇒
⇒
Слайд 14Теорема: Если при пересечении двух прямых секущей сумма односторонних углов равна
Дано:
а
b
с
а, b – прямые,
с – секущая,
∠1+∠4=180⁰
3
1
Доказать:
а||b
Доказательство:
2
∠3 и ∠4 – смежные ⇒
и т.к. ∠1+∠4=180⁰ (по усл.) ⇒
∠1=∠3 –
– накрест лежащие углы при прямых а и b и секущей с
⇒
а||b.
4
∠3 +∠4=180⁰
Доказано.