лежащим в плоскости, то она перпендикулярна к этой плоскости.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признак перпендикулярности прямой и плоскости презентация
Содержание
- 1. Признак перпендикулярности прямой и плоскости
- 2. Теорема. Если одна из двух параллельных
- 3. Обратная теорема. Если две прямые перпендикулярны к плоскости, то они параллельны.
- 4. Задача. Дано: a – прямая; M –
- 5. Задача. Дано: a – прямая; M
- 6. Задача. Дано: a –
- 7. Теорема. Через любую точку пространства проходит
- 8. Теорема. Через любую точку пространства проходит
- 9. Теорема. Через любую точку пространства
- 10. Задача. Дано: AD = 16 см;
- 11. Задача. Дано: Доказательство: Доказать:
- 12. Задача. Дано: Доказательство: Доказать:
Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Слайд 1
Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна двум пересекающимся прямым
Слайд 2
Теорема.
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и
другая прямая перпендикулярна к этой плоскости.
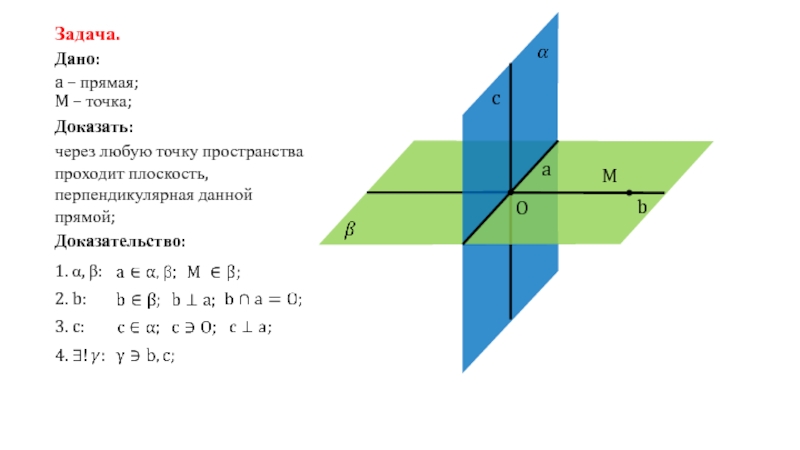
Слайд 4Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку пространства проходит плоскость, перпендикулярная
данной прямой;
Доказательство:
1. α, β:
M
a
Слайд 5
Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку пространства проходит плоскость, перпендикулярная
данной прямой;
Доказательство:
1. α, β:
2. b:
3. c:
a
M
b
O
c
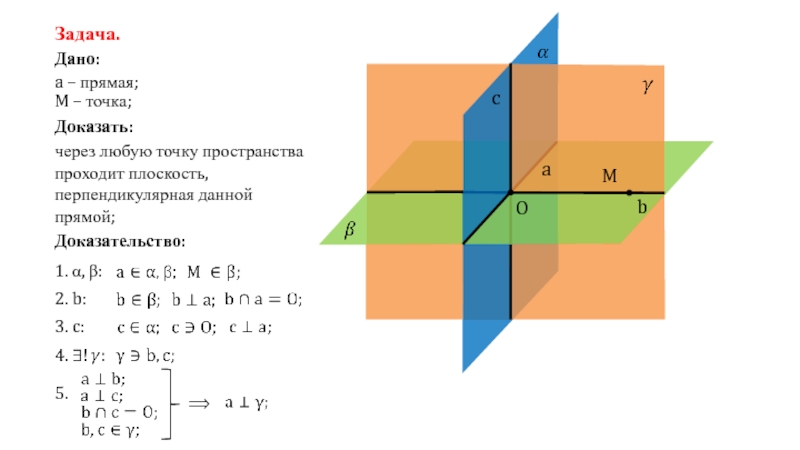
Слайд 6
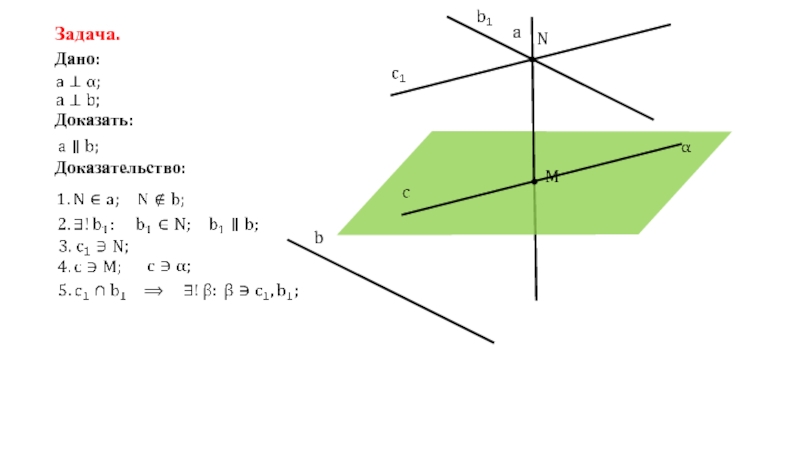
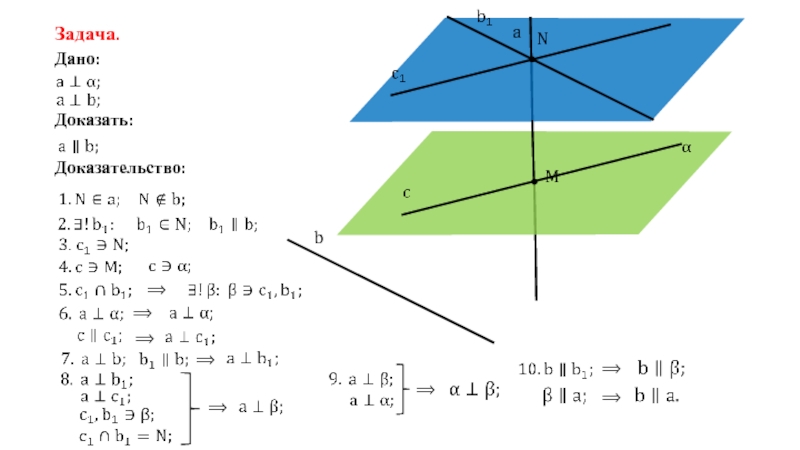
Задача.
Дано:
a – прямая;
M – точка;
Доказать:
через любую точку пространства проходит плоскость, перпендикулярная
данной прямой;
Доказательство:
1. α, β:
2. b:
3. c:
5.
⟹
b
c
a
M
O
Слайд 7
Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и
притом только одна.
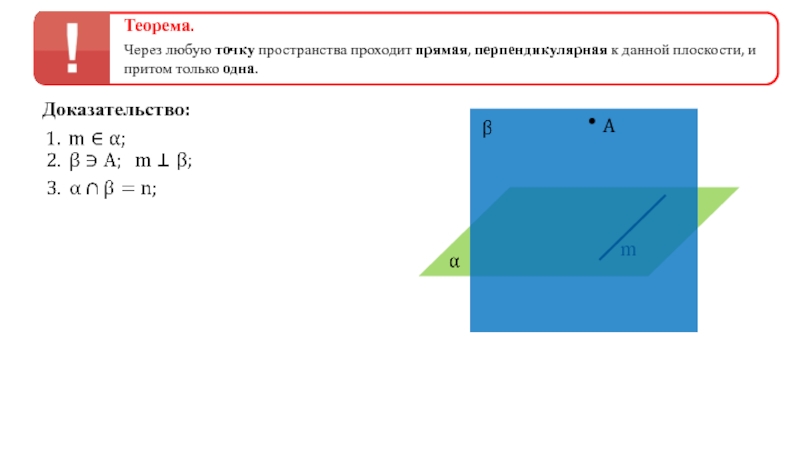
Слайд 8
Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и
притом только одна.
Доказательство:
m
A
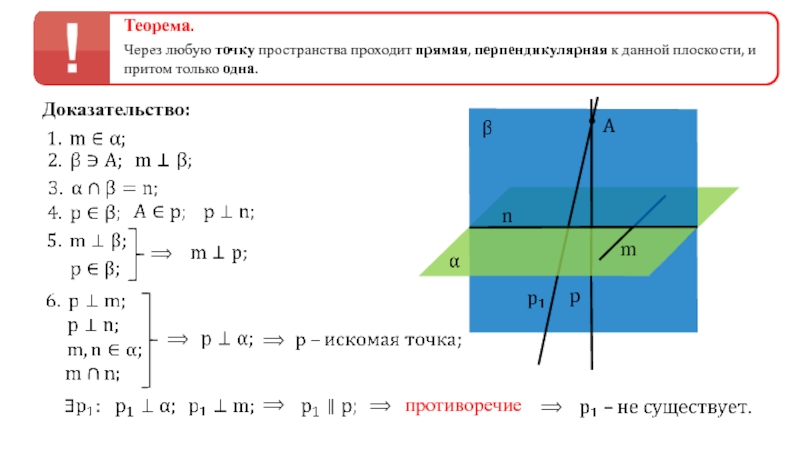
Слайд 9
Теорема.
Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и
притом только одна.
Доказательство:
m
n
A
p
⟹
⟹
⟹
⟹
⟹
противоречие
⟹
Слайд 10
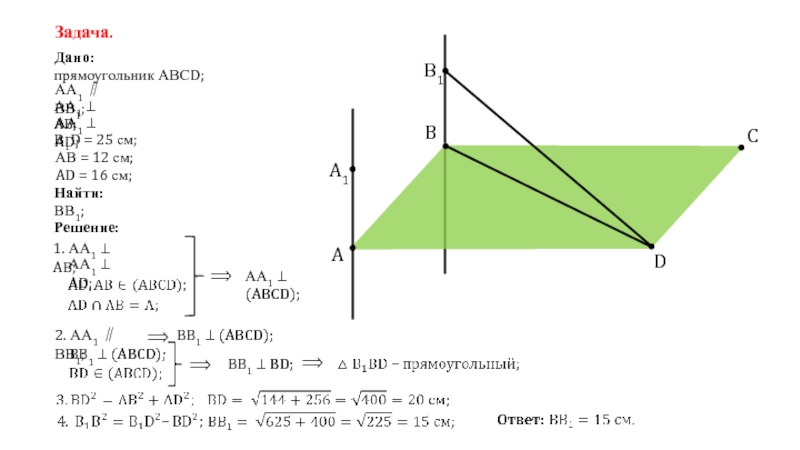
Задача.
Дано:
AD = 16 см;
Решение:
прямоугольник АВСD;
АА1 ∥ ВВ1;
АА1 ⊥ AB;
АА1 ⊥
AD;
В1D = 25 см;
АВ = 12 см;
Найти:
ВВ1;
A
B
C
D
В1
A1
1. АА1 ⊥ AB;
АА1 ⊥ AD;
⟹
АА1 ⊥ (ABCD);
2. АА1 ∥ ВВ1;
⟹
BB1 ⊥ (ABCD);
BB1 ⊥ (ABCD);
⟹
BB1 ⊥ BD;
⟹
