- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Представление рациональных чисел в виде десятичной дроби (продолжение) презентация
Содержание
- 1. Представление рациональных чисел в виде десятичной дроби (продолжение)
- 2. Теорема: для того , чтобы несократимая
- 3. Заметим, что в данной теореме речь идет
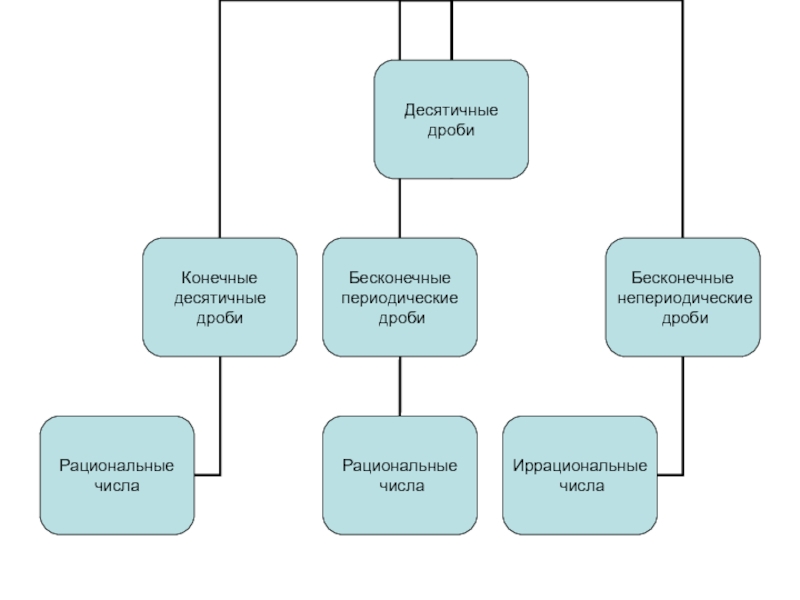
- 4. Конечная десятичная дробь – дробь, возникающая при
- 5. Любая конечная десятичная дробь может быть представлена в виде бесконечной десятичной дробью. 0,25=0,250=0,250000…0
- 7. Теорема: Любое положительное рациональное число представимо бесконечной периодической десятичной дробью.
- 9. Число, которое можно записать в виде бесконечной
- 10. Источником возникновения иррациональных чисел связано с измерением
- 11. Теорема: если единицей длины является длина стороны
- 12. Доказательство: A B C
- 13. По теореме Пифагора имеем: m-четное
- 14. Пусть m=2p. Значит, и
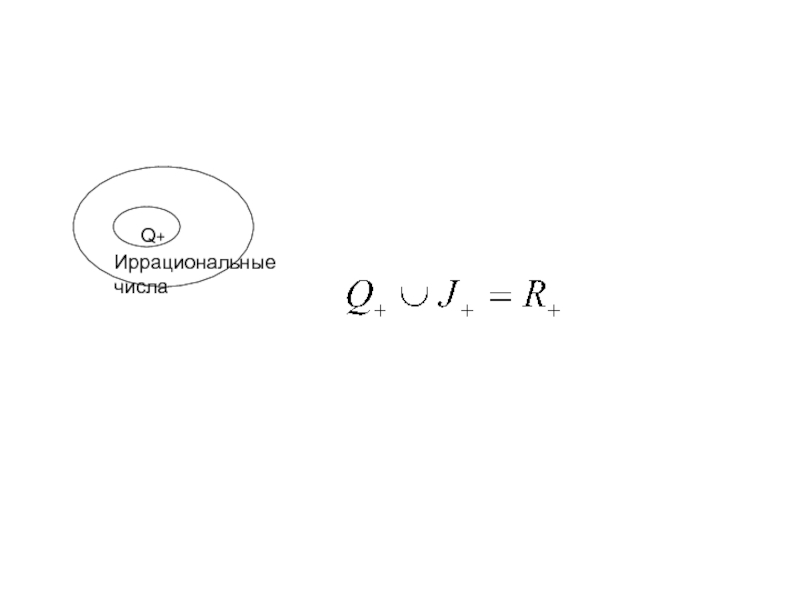
- 15. Q+ Иррациональные числа
- 16. Натуральное число как мера величины
- 17. Положительные скалярные величины Определение: положительной скалярной величиной
- 18. Например: длина (расстояние, ширина, протяженность) масса площадь, время, объем, стоимость, количество товара.
- 19. Величины, которые выражают одно и тоже свойство
- 20. Свойства однородных величин 1. Однородные величины можно
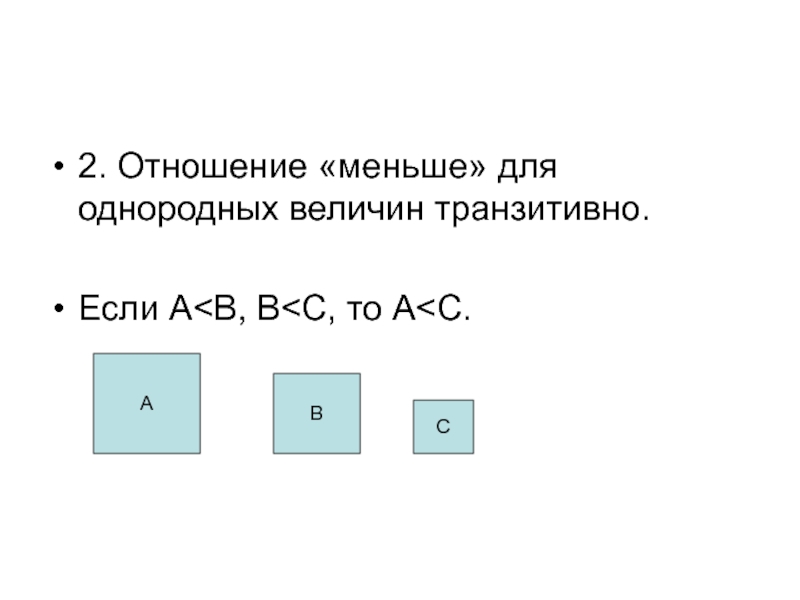
- 21. 2. Отношение «меньше» для однородных величин транзитивно. Если A
- 22. 3. Величины одного рода можно складывать, в
- 23. 4. Величины одного рода можно вычитать, в
- 24. 5. Величину можно умножать на положительное действительное
- 25. 6. величины одного рода можно делить, получая
- 26. Измерение величин Измерить величину A –это значит
- 27. Замечание: Величина, которая определяется одним численным значение,
- 28. Измерение величин позволяет переходить от сравнения величин
- 29. 1. Если величиныA и B измерены при
- 30. 2. Если величины A и B измерены
- 31. 3. Если величины A и B таковы,
- 32. Пешеход прошел 3 км. Объект:
- 33. Спасибо за внимание!
Теорема: для того , чтобы несократимая дробь была равна десятичной, необходимо и достаточно, чтобы в разложении ее знаменателя n на простые множители входили лишь числа
Слайд 2Теорема: для того , чтобы
несократимая дробь
была равна
десятичной, необходимо и достаточно, чтобы в разложении ее знаменателя n на простые множители входили лишь числа 2 и 5.
десятичной, необходимо и достаточно, чтобы в разложении ее знаменателя n на простые множители входили лишь числа 2 и 5.
Слайд 4Конечная десятичная дробь – дробь, возникающая при делении числителя на знаменатель,
когда найдется остаток, равный нулю.
Слайд 5Любая конечная десятичная дробь может быть представлена в виде бесконечной десятичной
дробью.
0,25=0,250=0,250000…0
0,25=0,250=0,250000…0
Слайд 7Теорема: Любое положительное рациональное число представимо бесконечной периодической десятичной дробью.
Слайд 9Число, которое можно записать в виде бесконечной непериодической дроби, называют иррациональным
числом.
Все такие числа составляют множество иррациональных чисел.
Все такие числа составляют множество иррациональных чисел.
Слайд 10Источником возникновения иррациональных чисел связано с измерением отрезков.
Существуют отрезки, длины которых
нельзя выразить рациональным числом при выбранной единице измерения.
Слайд 11Теорема: если единицей длины является длина стороны квадрата, то длина диагонали
этого квадрата не может быть выражена положительным рациональным числом.
Слайд 13По теореме Пифагора имеем:
m-четное число, так как квадрат нечетного числа не
может быть четным
Слайд 14Пусть m=2p.
Значит, и n – четное число, тогда дробь сократима
Противоречие. Значит
наше предположение не верно.
Слайд 17Положительные скалярные величины
Определение: положительной скалярной величиной называется свойство предмета, которое проявляется
при сравнении и для обозначения которого существуют стандартные единицы измерения
Слайд 18Например: длина (расстояние, ширина, протяженность)
масса
площадь,
время,
объем,
стоимость,
количество товара.
Слайд 19Величины, которые выражают одно и тоже свойство объектов, называются величинами одного
рода.
(однородными величинами)
(однородными величинами)
Слайд 20Свойства однородных величин
1. Однородные величины можно сравнивать.
Для любых однородных величин A
и B имеет место только из отношений
A>B или A=B или A
A>B или A=B или A
Слайд 223. Величины одного рода можно складывать, в результате получается величина того
же рода.
Сложение однородных величин, коммутативно и ассоциативно.
Сложение однородных величин, коммутативно и ассоциативно.
Слайд 234. Величины одного рода можно вычитать, в результате получается величина того
же рода.
Определяют вычитание через сложение: если C=A-B, то A=B+C
Определяют вычитание через сложение: если C=A-B, то A=B+C
Слайд 245. Величину можно умножать на положительное действительное число, в результате получают
величину того же рода.
B=x∙A
B=x∙A
Слайд 256. величины одного рода можно делить, получая в результате число.
Частным величин
A и B называется такое положительное действительное число x=A:B, что A=x∙B.
Слайд 26Измерение величин
Измерить величину A –это значит найти такое положительное действительное число
x, что A=x∙E.
Число x называется численным значением величины A при единице измерения величины E.
Число x называется численным значением величины A при единице измерения величины E.
Слайд 27Замечание:
Величина, которая определяется одним численным значение, называется скалярной величиной.
Если при выбранной
единице измерения скалярная величина принимает только положительные численные значения, то ее называют положительной скалярной величиной
Слайд 28Измерение величин позволяет переходить от сравнения величин к сравнению чисел, от
действий над величинами к соответствующим действиям над числами.
Слайд 291. Если величиныA и B измерены при помощи единицы величины E,
отношение между величинами A и B будут такими же. Как и отношения между их численными значениями и наоборот:
A=B m(A)=m(B);
AA>B m(A)>m(B)
A=B m(A)=m(B);
AA>B m(A)>m(B)
Слайд 302. Если величины A и B измерены при помощи единицы величины
E, то для нахождения численного значения суммы A+B достаточно сложить численные значения величин A и B.
A+B=C m(A+B)=m(A)+m(B)
A+B=C m(A+B)=m(A)+m(B)
Слайд 313. Если величины A и B таковы, что B=x∙A, где x
– положительное действительное число, и величина A измерена при помощи единицы величины E, то чтобы найти численное значение величины B при единице E, достаточно число x умножить на число m(A).
B=x∙A m(A)=x∙m(B)
B=x∙A m(A)=x∙m(B)
Слайд 32 Пешеход прошел 3 км.
Объект: расстояние,
Свойство объекта – длина
Единица измерения –километр
Численное
значение величины равно 3.
