- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение графиков функций элементарными средствами презентация
Содержание
- 1. Построение графиков функций элементарными средствами
- 2. Представим себе, что нам известен график некоторой
- 3. Введение Мы с вами научимся строить
- 4. Укажем правила построения Гg
- 5. g(x) = f(x) + a Гg
- 6. g(x) = f(x + a)
- 7. g(x) = - f(x)
- 8. g(x) = f(-x) Гg получается
- 9. Гg получается из Гf так:
- 10. Гg получается из Гf так:
- 11. Искомое множество точек получается из
- 12. g(x) = a f(x) , где a
- 13. g(x) = f(a x) , где a
- 14. Счастливо упражняться !!!
- 15. g(x) = f(x) + a Гg
- 16. g(x) = f(x) + a Гg
- 17. g(x) = f(x + a)
- 18. g(x) = f(x + a)
- 19. g(x) = - f(x)
- 20. g(x) = f(-x) Гg получается
- 21. Гg получается из Гf так:
- 22. Гg получается из Гf так:
- 23. Искомое множество точек получается из
- 24. g(x) = a f(x) , где a
- 25. g(x) = a f(x) , где a
- 26. g(x) = f(a x) , где a
- 27. g(x) = f(a x) , где a
Представим себе, что нам известен график некоторой функции f(x), который мы договоримся называть «старым» и будем обозначать Гf . Поставим задачу построения
Слайд 2Представим себе, что нам известен график некоторой функции f(x),
который мы договоримся называть «старым» и будем обозначать Гf .
Поставим задачу построения графика другой функции g(x), определённым образом связанной со «старой» функцией , используя «старый» график в качестве исходного. Искомый график назовём «новым» и будем обозначать Гg .
Поставим задачу построения графика другой функции g(x), определённым образом связанной со «старой» функцией , используя «старый» график в качестве исходного. Искомый график назовём «новым» и будем обозначать Гg .
Слайд 3Введение
Мы с вами научимся строить графики различных элементарных функций без
применения производной. Такие методы построения графиков мы и будем называть элементарными.
Слайд 4
Укажем правила построения Гg из Гf
в зависимости
от того, каким образом связаны f(x) и g(x) .
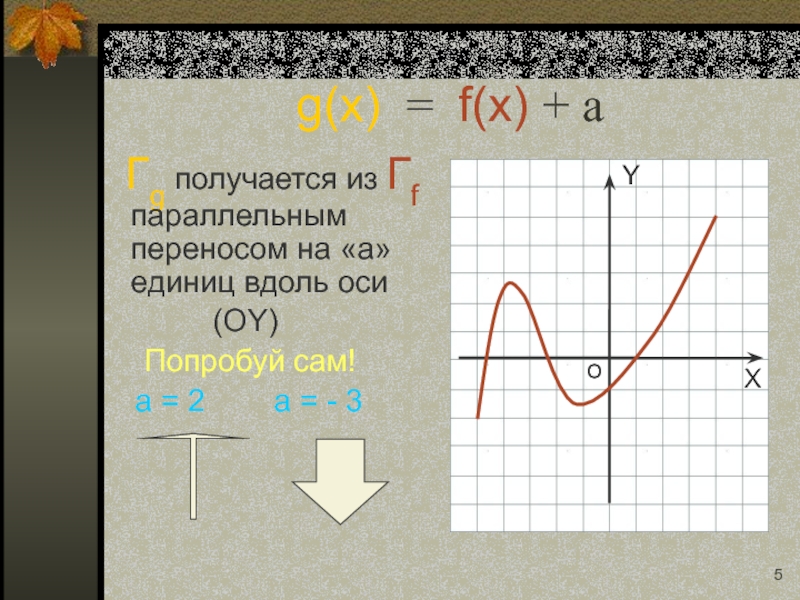
Слайд 5g(x) = f(x) + a
Гg получается из Гf параллельным переносом
на «a» единиц вдоль оси
(OY)
Попробуй сам!
a = 2 a = - 3
(OY)
Попробуй сам!
a = 2 a = - 3
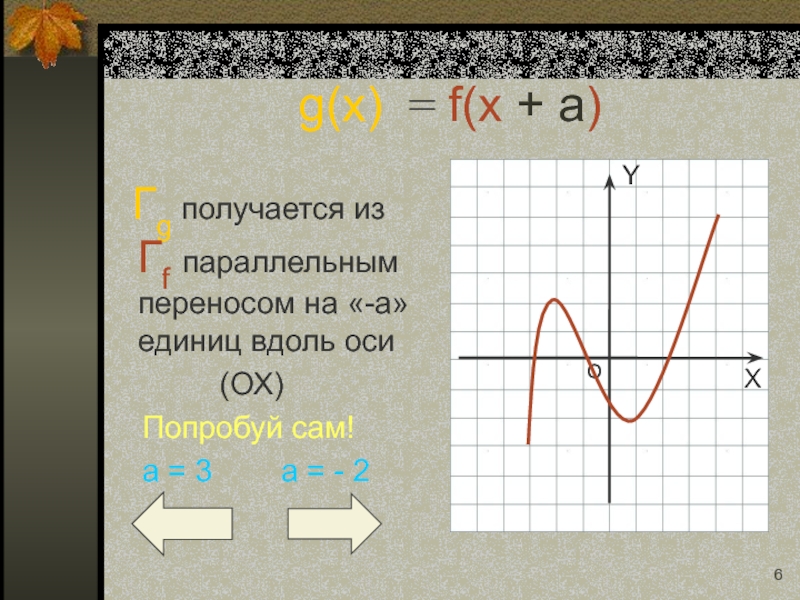
Слайд 6g(x) = f(x + a)
Гg получается из Гf
параллельным переносом на «-a» единиц вдоль оси
(ОХ)
Попробуй сам!
a = 3 a = - 2
(ОХ)
Попробуй сам!
a = 3 a = - 2
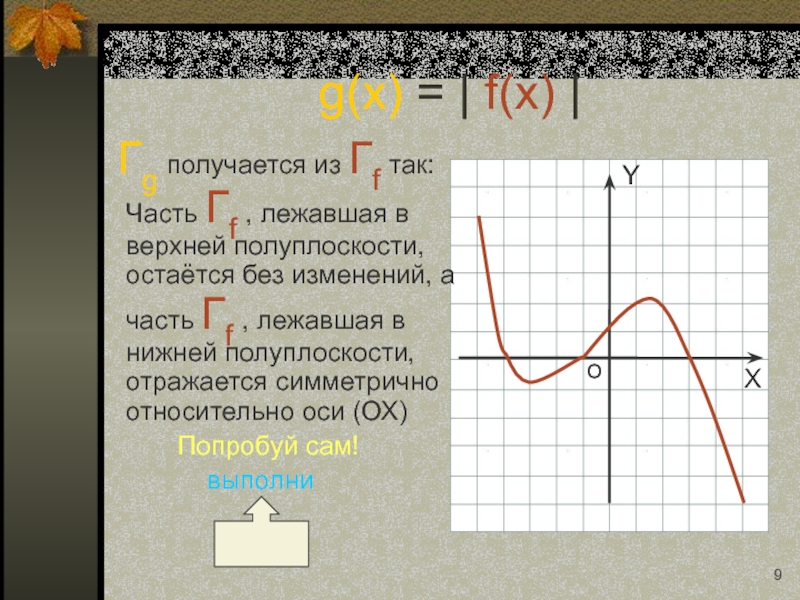
Слайд 9 Гg получается из Гf так: Часть Гf , лежавшая
в верхней полуплоскости, остаётся без изменений, а часть Гf , лежавшая в нижней полуплоскости, отражается симметрично относительно оси (ОХ)
Попробуй сам!
выполни
Попробуй сам!
выполни
g(x) = | f(x) |
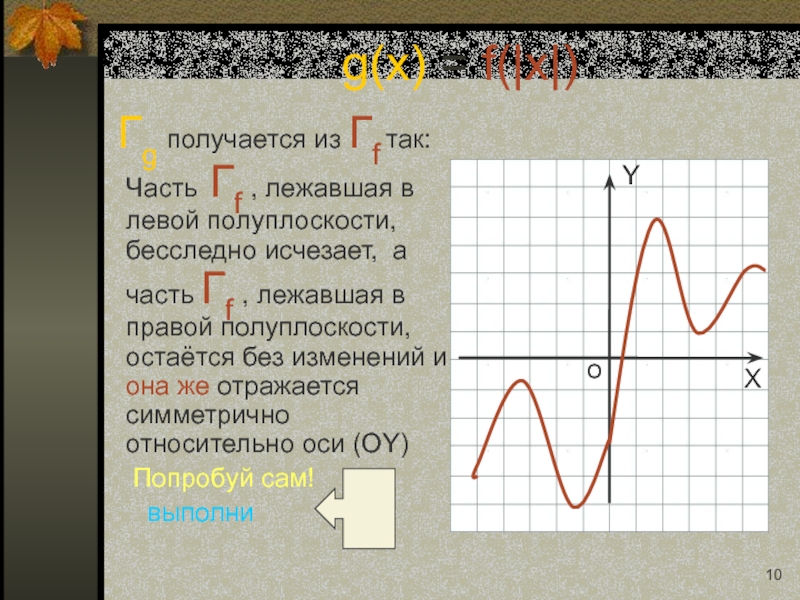
Слайд 10 Гg получается из Гf так: Часть Гf , лежавшая
в левой полуплоскости, бесследно исчезает, а часть Гf , лежавшая в правой полуплоскости, остаётся без изменений и она же отражается симметрично относительно оси (ОY)
Попробуй сам!
выполни
Попробуй сам!
выполни
g(x) = f(|x|)
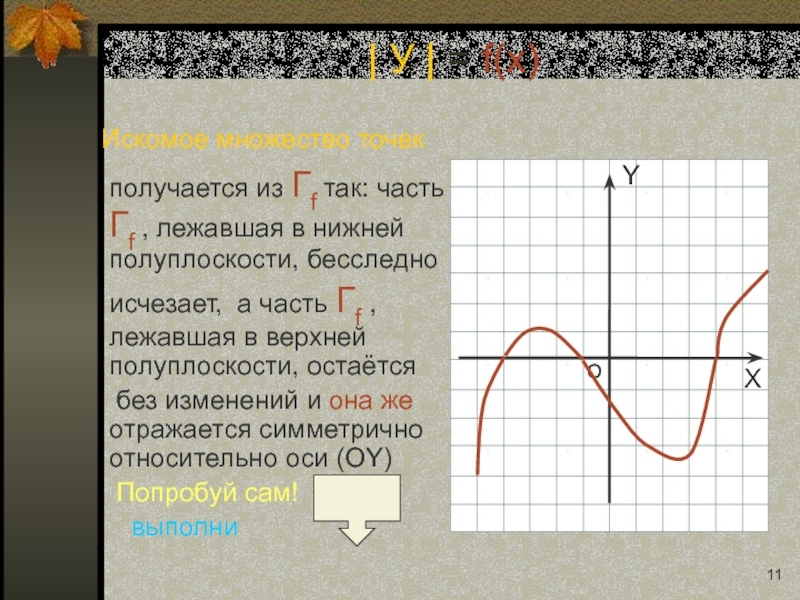
Слайд 11 Искомое множество точек получается из Гf так: часть Гf
, лежавшая в нижней полуплоскости, бесследно исчезает, а часть Гf , лежавшая в верхней полуплоскости, остаётся
без изменений и она же отражается симметрично относительно оси (ОY)
Попробуй сам!
выполни
без изменений и она же отражается симметрично относительно оси (ОY)
Попробуй сам!
выполни
| У | = f(x)
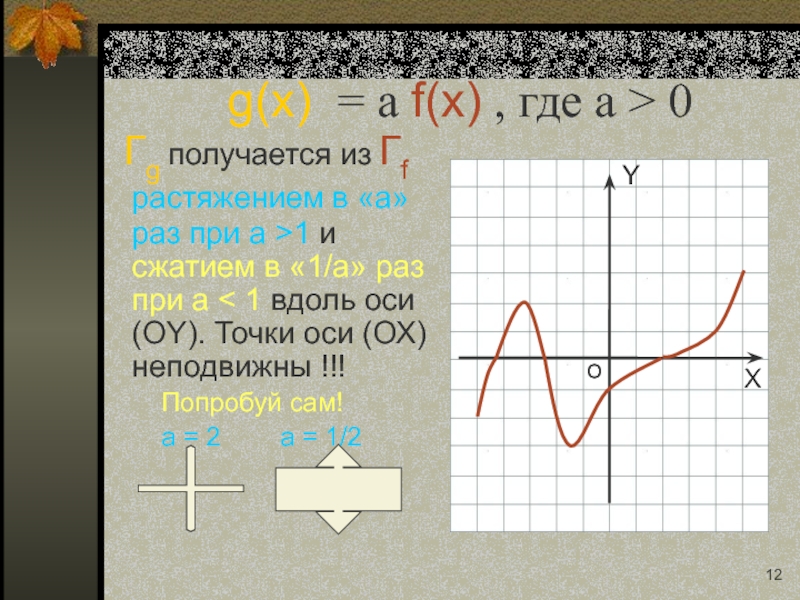
Слайд 12g(x) = a f(x) , где a > 0
Гg получается
из Гf растяжением в «a» раз при a >1 и сжатием в «1/a» раз при a < 1 вдоль оси (OY). Точки оси (ОХ) неподвижны !!!
Попробуй сам!
a = 2 a = 1/2
Попробуй сам!
a = 2 a = 1/2
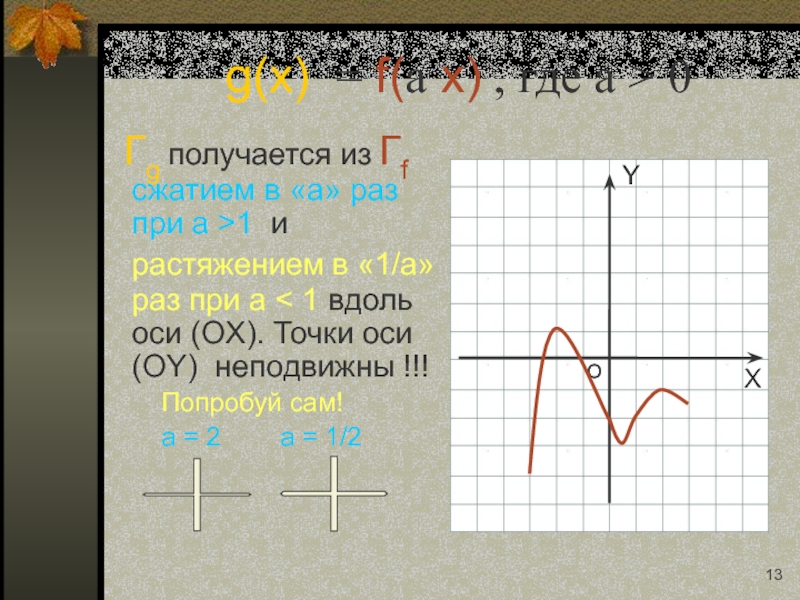
Слайд 13g(x) = f(a x) , где a > 0
Гg получается
из Гf сжатием в «a» раз при a >1 и растяжением в «1/a» раз при a < 1 вдоль оси (OХ). Точки оси (OY) неподвижны !!!
Попробуй сам!
a = 2 a = 1/2
Попробуй сам!
a = 2 a = 1/2
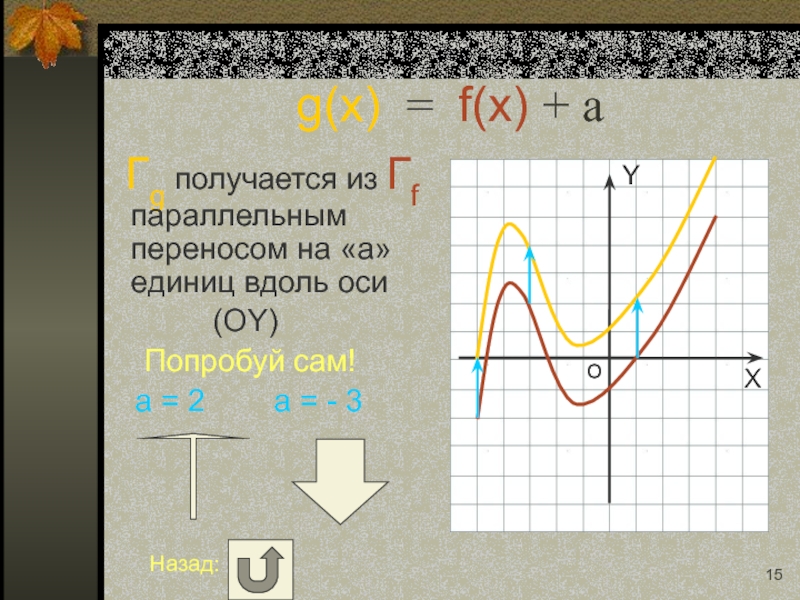
Слайд 15g(x) = f(x) + a
Гg получается из Гf параллельным переносом
на «a» единиц вдоль оси
(OY)
Попробуй сам!
a = 2 a = - 3
Назад:
(OY)
Попробуй сам!
a = 2 a = - 3
Назад:
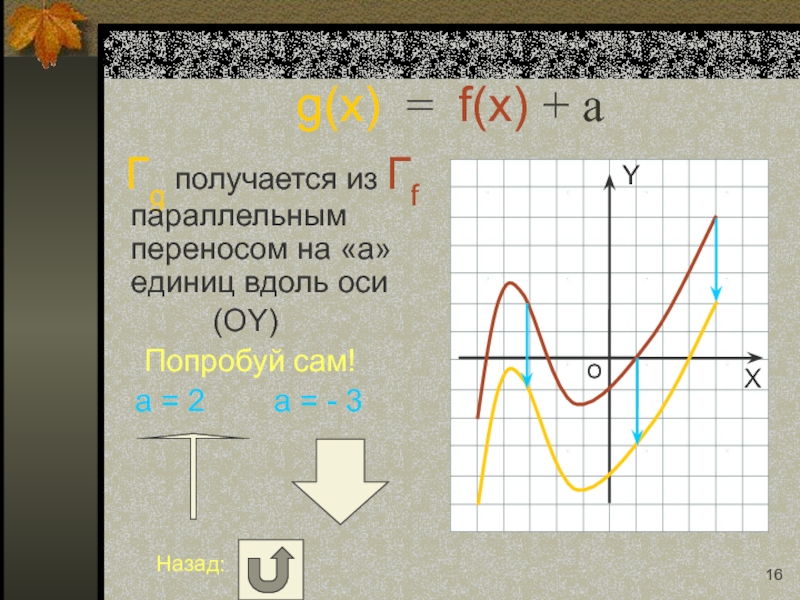
Слайд 16g(x) = f(x) + a
Гg получается из Гf параллельным переносом
на «a» единиц вдоль оси
(OY)
Попробуй сам!
a = 2 a = - 3
Назад:
(OY)
Попробуй сам!
a = 2 a = - 3
Назад:
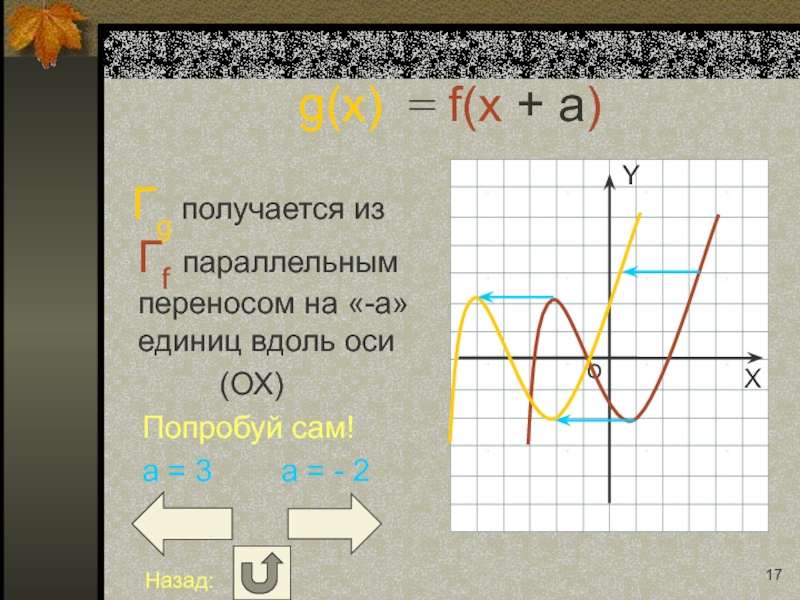
Слайд 17g(x) = f(x + a)
Гg получается из Гf
параллельным переносом на «-a» единиц вдоль оси
(ОХ)
Попробуй сам!
a = 3 a = - 2
Назад:
(ОХ)
Попробуй сам!
a = 3 a = - 2
Назад:
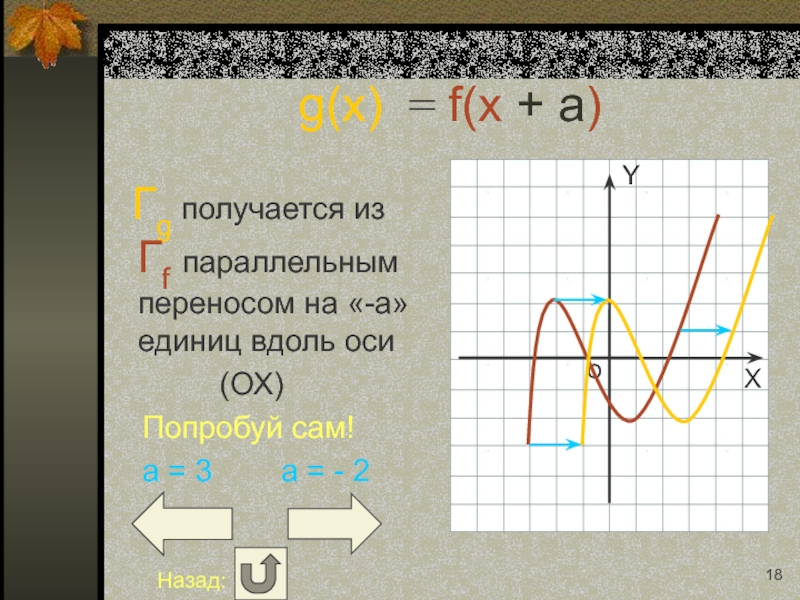
Слайд 18g(x) = f(x + a)
Гg получается из Гf
параллельным переносом на «-a» единиц вдоль оси
(ОХ)
Попробуй сам!
a = 3 a = - 2
Назад:
(ОХ)
Попробуй сам!
a = 3 a = - 2
Назад:
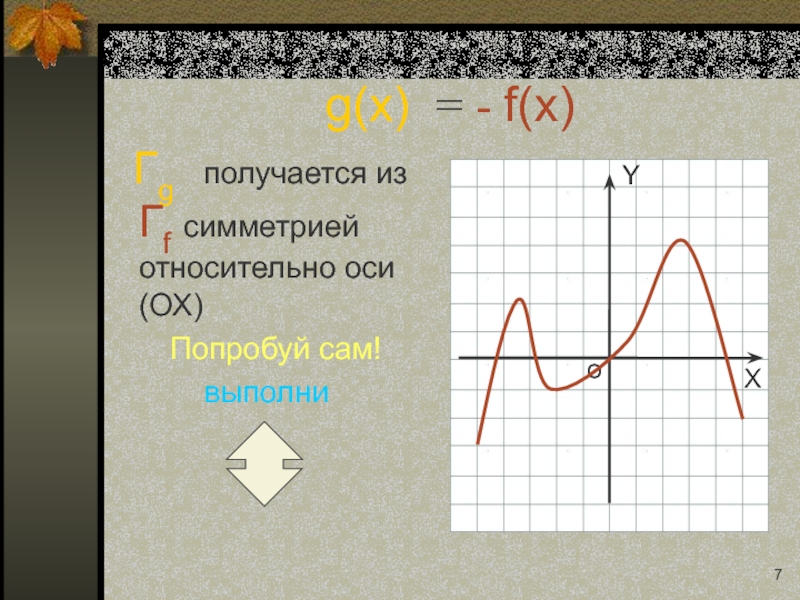
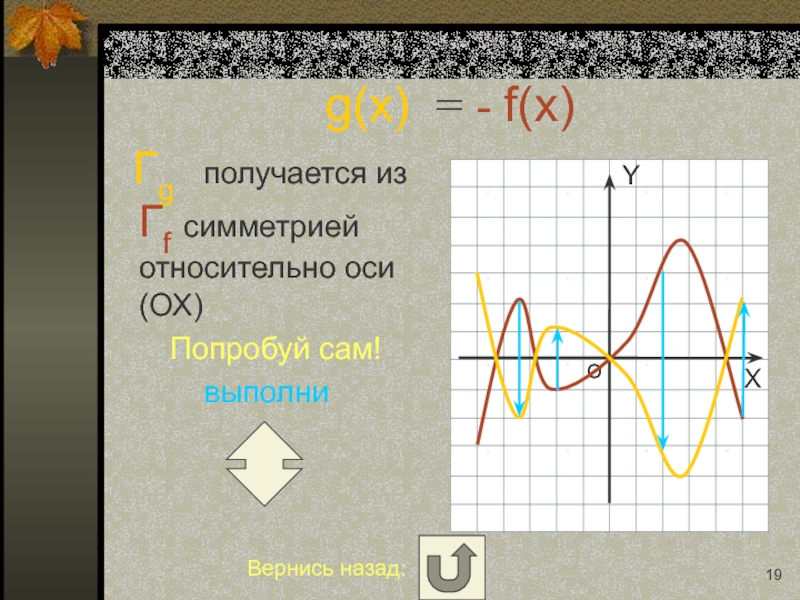
Слайд 19g(x) = - f(x)
Гg получается из Гf
симметрией относительно оси (ОХ)
Попробуй сам!
выполни
Вернись назад:
Попробуй сам!
выполни
Вернись назад:
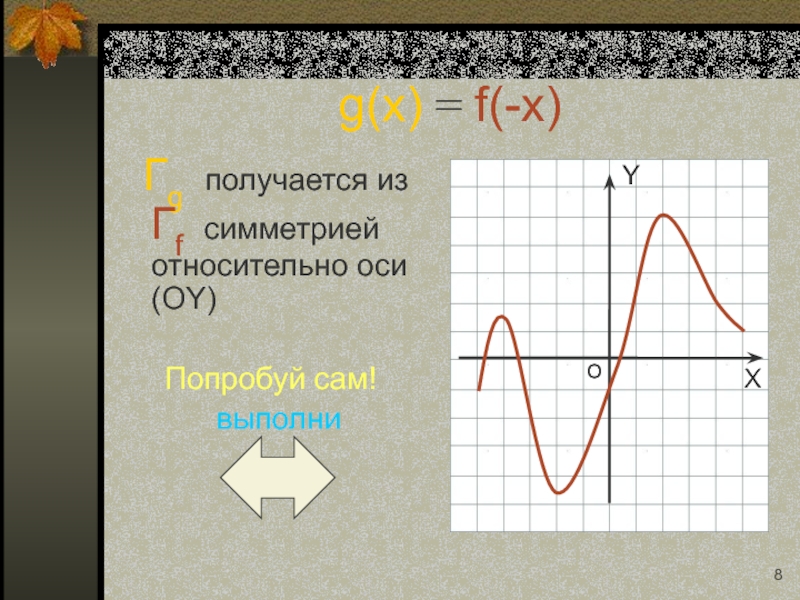
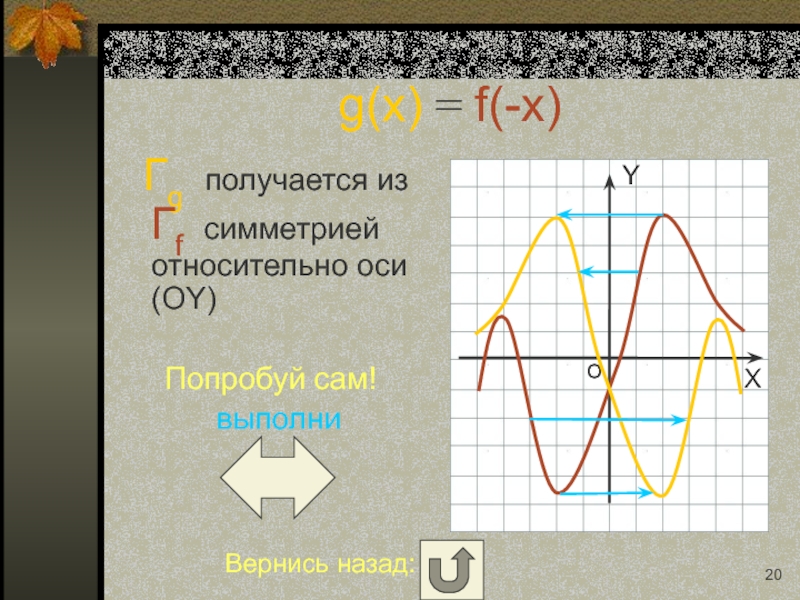
Слайд 20g(x) = f(-x)
Гg получается из Гf симметрией относительно оси
(OY)
Попробуй сам!
выполни
Вернись назад:
Попробуй сам!
выполни
Вернись назад:
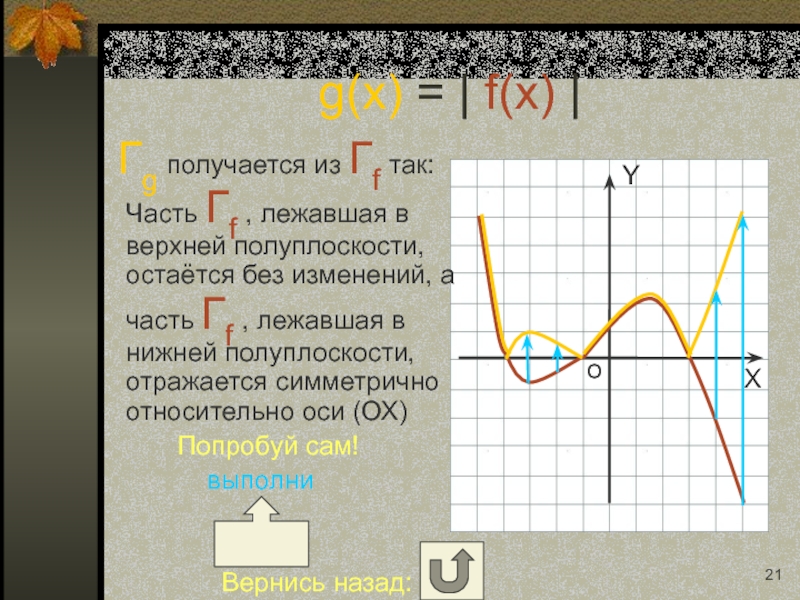
Слайд 21 Гg получается из Гf так: Часть Гf , лежавшая
в верхней полуплоскости, остаётся без изменений, а часть Гf , лежавшая в нижней полуплоскости, отражается симметрично относительно оси (ОХ)
Попробуй сам!
выполни
Вернись назад:
Попробуй сам!
выполни
Вернись назад:
g(x) = | f(x) |
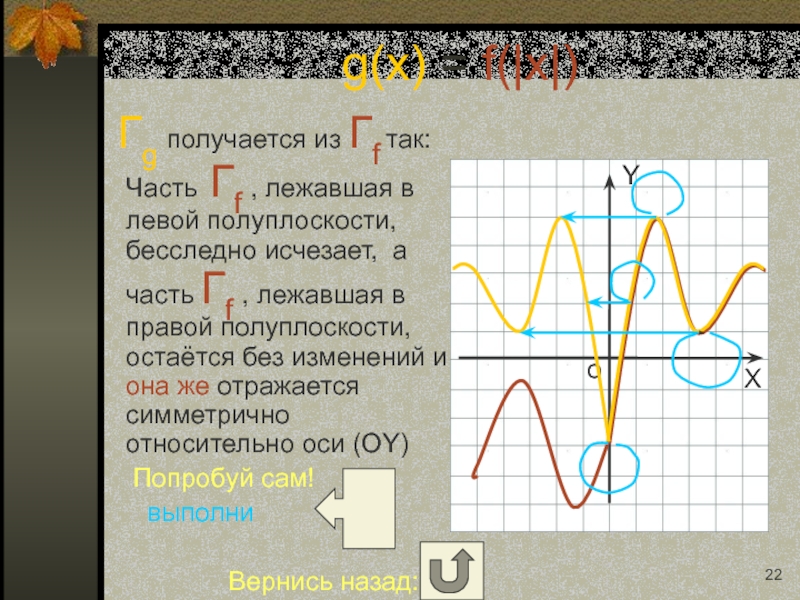
Слайд 22 Гg получается из Гf так: Часть Гf , лежавшая
в левой полуплоскости, бесследно исчезает, а часть Гf , лежавшая в правой полуплоскости, остаётся без изменений и она же отражается симметрично относительно оси (ОY)
Попробуй сам!
выполни
Вернись назад:
Попробуй сам!
выполни
Вернись назад:
g(x) = f(|x|)
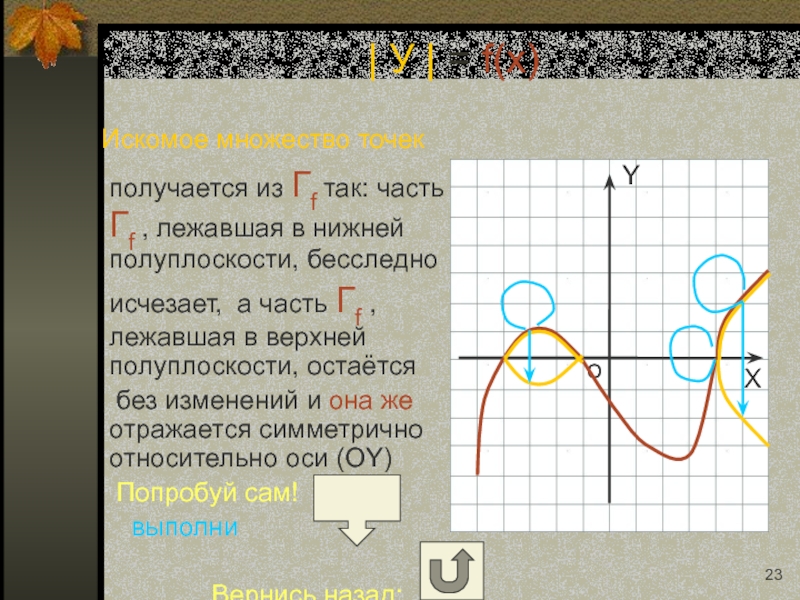
Слайд 23 Искомое множество точек получается из Гf так: часть Гf
, лежавшая в нижней полуплоскости, бесследно исчезает, а часть Гf , лежавшая в верхней полуплоскости, остаётся
без изменений и она же отражается симметрично относительно оси (ОY)
Попробуй сам!
выполни
Вернись назад:
без изменений и она же отражается симметрично относительно оси (ОY)
Попробуй сам!
выполни
Вернись назад:
| У | = f(x)
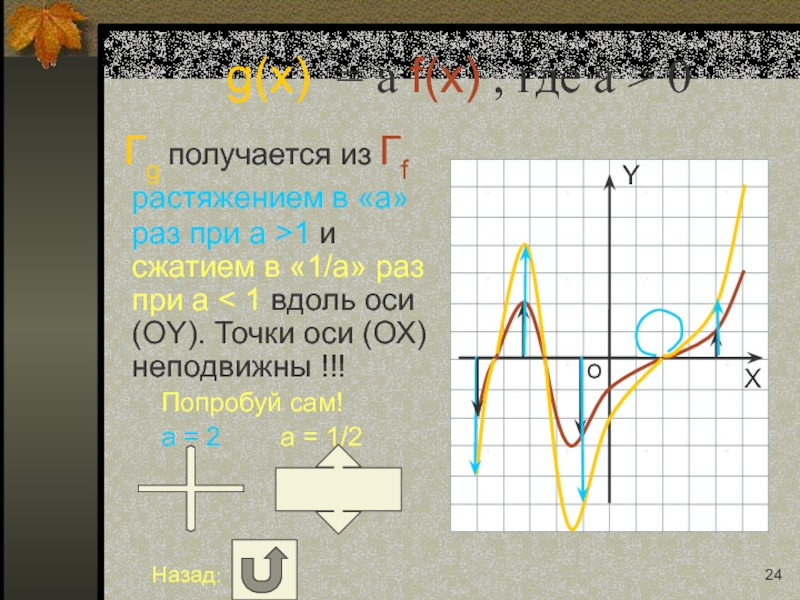
Слайд 24g(x) = a f(x) , где a > 0
Гg получается
из Гf растяжением в «a» раз при a >1 и сжатием в «1/a» раз при a < 1 вдоль оси (OY). Точки оси (ОХ) неподвижны !!!
Попробуй сам!
a = 2 a = 1/2
Назад:
Попробуй сам!
a = 2 a = 1/2
Назад:
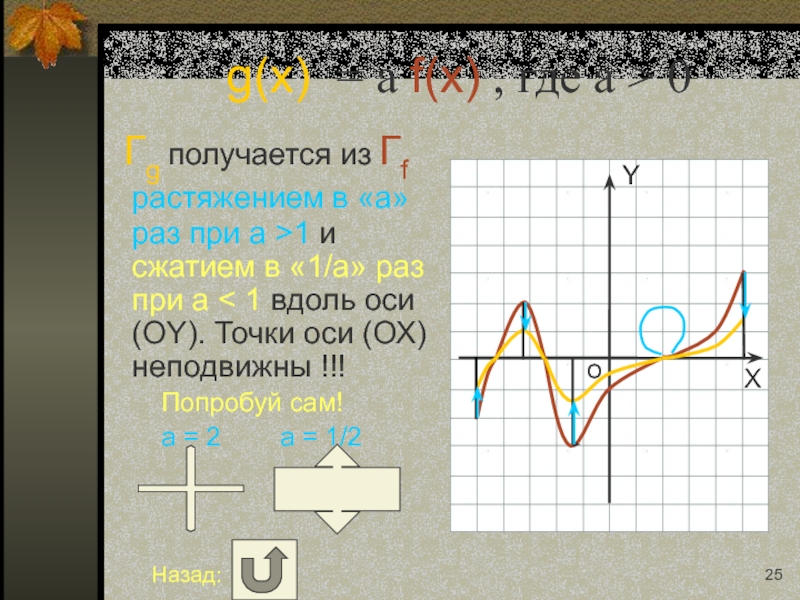
Слайд 25g(x) = a f(x) , где a > 0
Гg получается
из Гf растяжением в «a» раз при a >1 и сжатием в «1/a» раз при a < 1 вдоль оси (OY). Точки оси (ОХ) неподвижны !!!
Попробуй сам!
a = 2 a = 1/2
Назад:
Попробуй сам!
a = 2 a = 1/2
Назад:
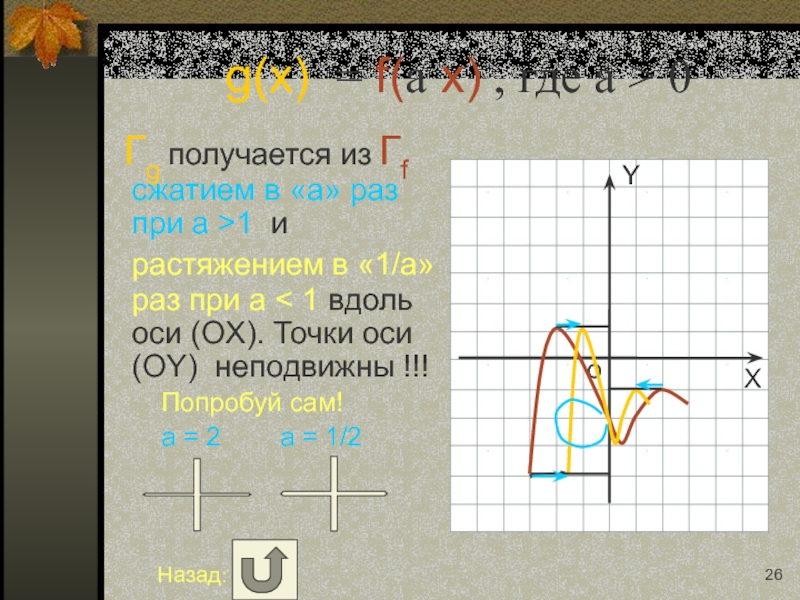
Слайд 26g(x) = f(a x) , где a > 0
Гg получается
из Гf сжатием в «a» раз при a >1 и растяжением в «1/a» раз при a < 1 вдоль оси (OХ). Точки оси (OY) неподвижны !!!
Попробуй сам!
a = 2 a = 1/2
Назад:
Попробуй сам!
a = 2 a = 1/2
Назад:
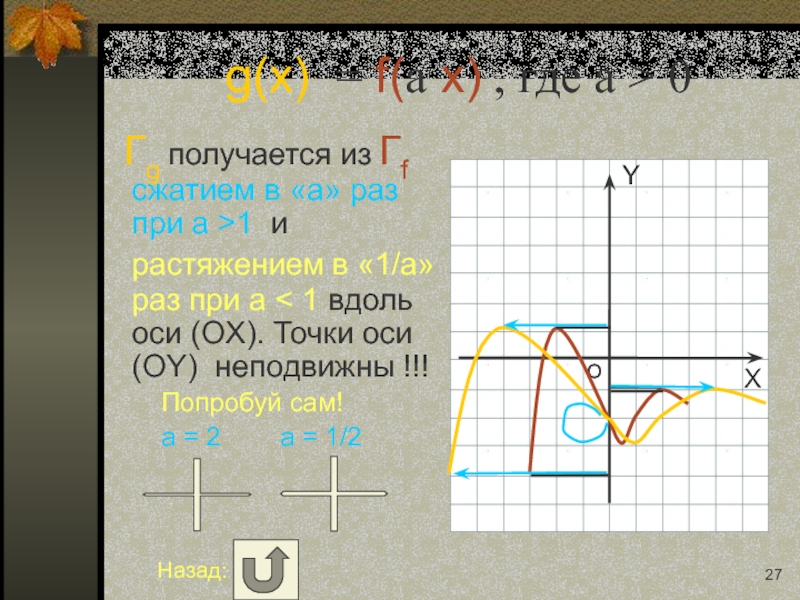
Слайд 27g(x) = f(a x) , где a > 0
Гg получается
из Гf сжатием в «a» раз при a >1 и растяжением в «1/a» раз при a < 1 вдоль оси (OХ). Точки оси (OY) неподвижны !!!
Попробуй сам!
a = 2 a = 1/2
Назад:
Попробуй сам!
a = 2 a = 1/2
Назад:
