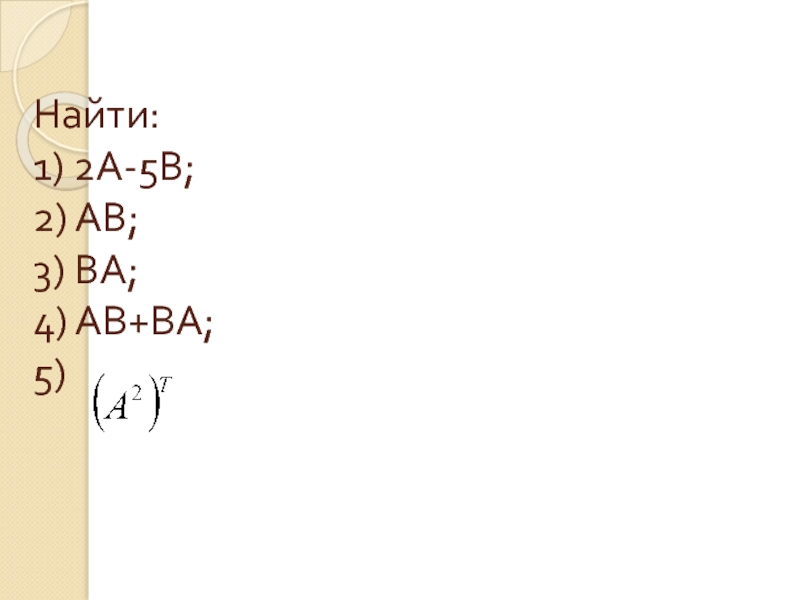- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Элементы линейной алгебры презентация
Содержание
- 1. Элементы линейной алгебры
- 2. Линейная алгебра. Основные сведения о матрицах.
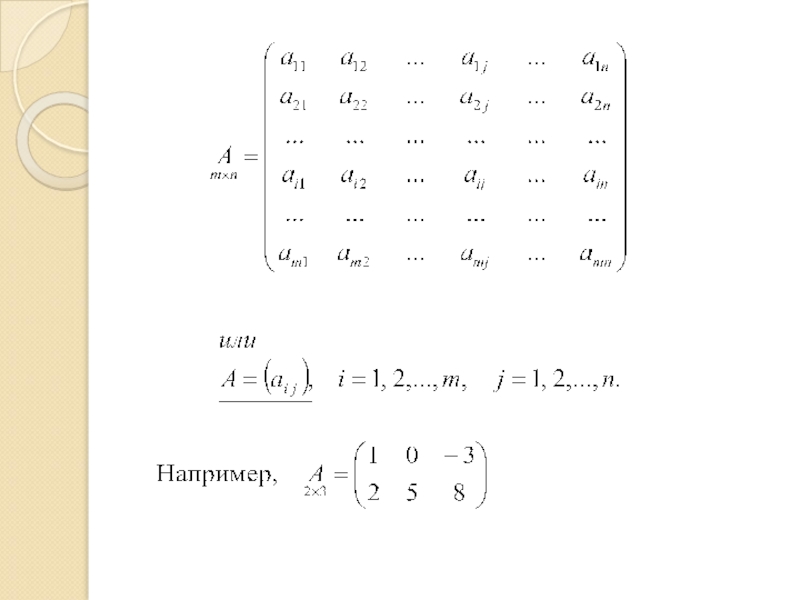
- 3. 1. Понятие матрицы Определение. Прямоугольная таблица чисел,
- 4. или
- 5. Определение. Две матрицы А и В одного
- 6. С помощью матриц удобно записывать некоторые экономические
- 7. 2. Виды матриц Определение. Матрица, состоящая из
- 8. Определение. Если число столбцов матрицы п равно
- 9. Определение. Квадратная матрица называется диагональной, если все
- 10. Если у диагональной матрицы п-го порядка все
- 11. Определение. Матрица любого размера называется нулевой
- 12. Определение. Квадратная матрица называется треугольной, если
- 13. 3. Операции над матрицами 1) Умножение матрицы
- 14. Например, Если
- 15. 2) Сложение матриц Определение. Суммой матриц А
- 16. Например,
- 17. 3) Вычитание матриц Определение. Разность двух матриц
- 18. 4) Умножение матриц. Матрицу А можно умножить
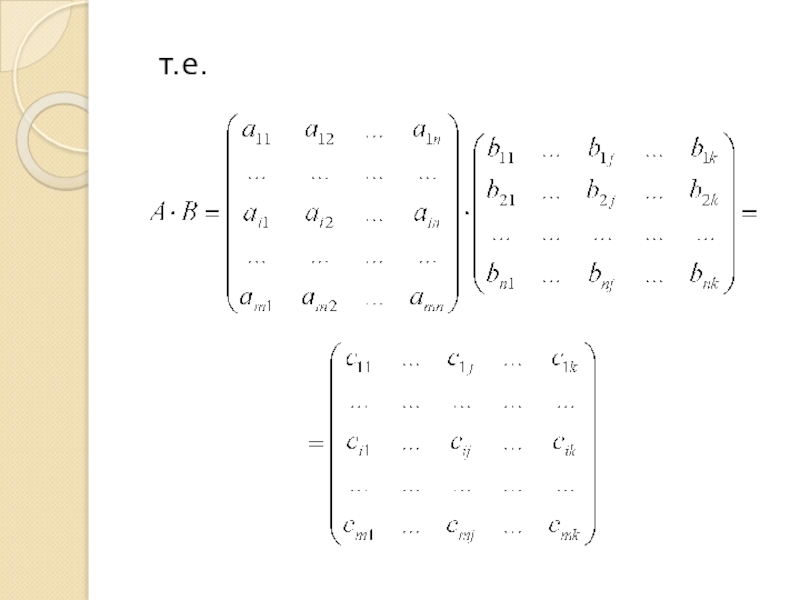
- 19. т.е.
- 20. Элементы матрицы С вычисляются по формуле:
- 21. Пример. Вычислить произведение матриц А ∙ В,
- 22. 5) Возведение в степень Определение. Целой положительной
- 23. Пример. Возвести матрицу A в квадрат и
- 24. 6) Транспонирование матрицы - переход от
- 25. Например, если
- 26. 4. Свойства операций над матрицами
- 27. Однако имеются и специфические свойства матриц. Если
- 28. 2) Если даже произведения А·В и
- 29. 3) Когда оба произведения А·В и В·А
- 30. Частный случай. Коммутативным законом обладает произведение любой
- 31. 4) Произведение двух ненулевых матриц может равняться
- 32. САМОСТОЯТЕЛЬНАЯ РАБОТА №1 Даны матрицы
- 33. Найти: 1) 2А-5В; 2) АВ; 3) ВА; 4) АВ+ВА; 5)
- 34. САМОСТОЯТЕЛЬНАЯ РАБОТА №1 пересдача Даны матрицы
Линейная алгебра.
Основные сведения о матрицах.
Виды и свойства матриц.
Операции над матрицами.
Слайд 2Линейная алгебра. Основные сведения о матрицах. Виды и свойства матриц. Операции
над матрицами.
Слайд 31. Понятие матрицы
Определение. Прямоугольная таблица чисел, содержащая т строк и п
столбцов, называется матрицей размера тхп.
Числа, составляющие матрицу – элементы матрицы. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.
Матрицы обозначаются заглавными буквами латинского алфавита (А, В, С, …), а элементы матрицы – строчными буквами с двойной индексацией ( , где i – номер строки,
j – номер столбца).
Матрицы записываются ( ), или [ ], или || ||.
Числа, составляющие матрицу – элементы матрицы. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.
Матрицы обозначаются заглавными буквами латинского алфавита (А, В, С, …), а элементы матрицы – строчными буквами с двойной индексацией ( , где i – номер строки,
j – номер столбца).
Матрицы записываются ( ), или [ ], или || ||.
Слайд 5Определение. Две матрицы А и В одного размера называются равными, если
они совпадают поэлементно, т.е. А = В, если для любых
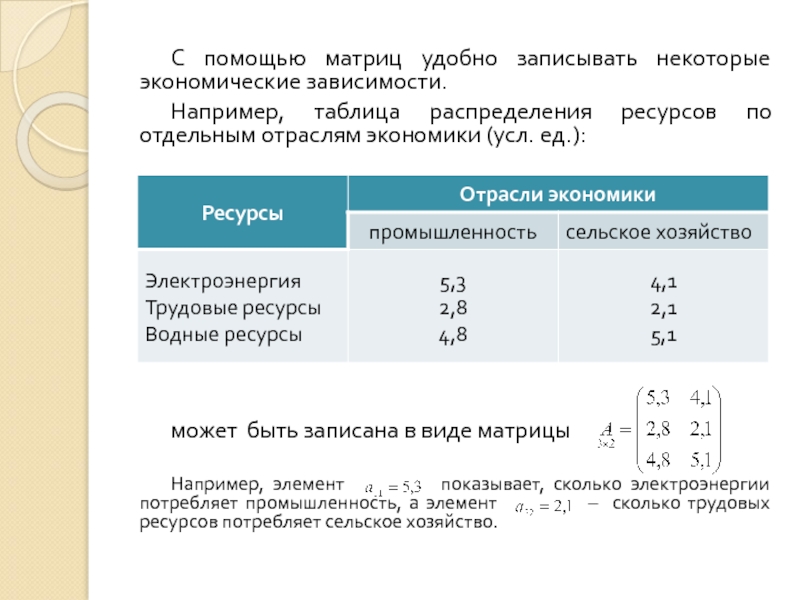
Слайд 6С помощью матриц удобно записывать некоторые экономические зависимости.
Например, таблица распределения
ресурсов по отдельным отраслям экономики (усл. ед.):
может быть записана в виде матрицы
Например, элемент показывает, сколько электроэнергии потребляет промышленность, а элемент – сколько трудовых ресурсов потребляет сельское хозяйство.
может быть записана в виде матрицы
Например, элемент показывает, сколько электроэнергии потребляет промышленность, а элемент – сколько трудовых ресурсов потребляет сельское хозяйство.
Слайд 72. Виды матриц
Определение. Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой,
а из одного столбца – матрицей-столбцом:
– матрица-строка
– матрица-столбец
Слайд 8Определение. Если число столбцов матрицы п равно числу ее строк, то
матрицу называют квадратной п-го порядка.
Ее элементы образуют главную диагональ матрицы.
Например,
– квадратные матрицы 3-го порядка.
Ее элементы образуют главную диагональ матрицы.
Например,
– квадратные матрицы 3-го порядка.
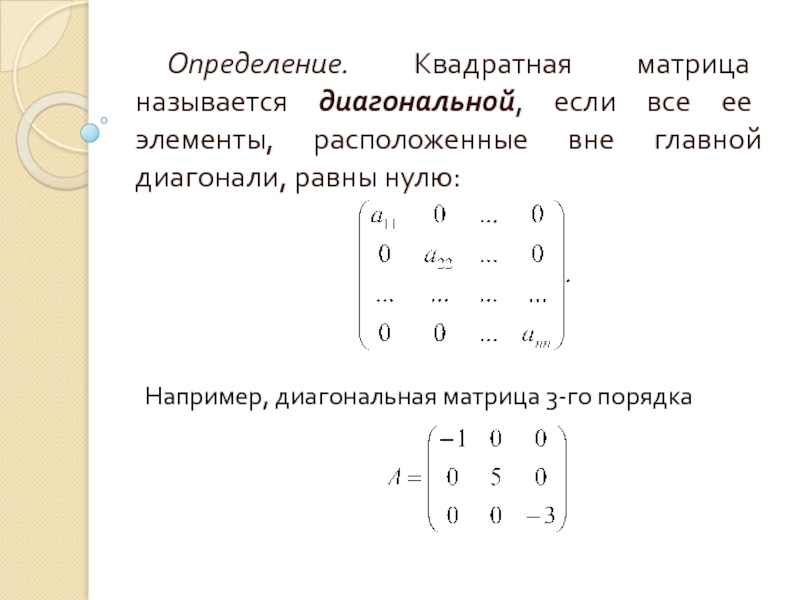
Слайд 9Определение. Квадратная матрица называется диагональной, если все ее элементы, расположенные вне
главной диагонали, равны нулю:
Например, диагональная матрица 3-го порядка
Слайд 10Если у диагональной матрицы п-го порядка все диагональные элементы равны единице,
то матрица называется единичной п-го порядка и обозначается буквой Е:
Например, единичная матрица 3-го порядка имеет вид
Слайд 11Определение.
Матрица любого размера называется нулевой или нуль – матрицей, если
все ее элементы равны нулю:
Слайд 12Определение.
Квадратная матрица называется треугольной, если все ее элементы, расположенные по
одну сторону от главной диагонали, равны нулю.
Например,
Например,
Слайд 133. Операции над матрицами
1) Умножение матрицы на число.
Определение. Произведением матрицы А
на число λ называется матрица В=λА, элементы которой для
Правило. Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число:
Правило. Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число:
Слайд 14Например,
Если
, то .
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например, .
Частный случай: произведение матрицы на число 0 есть нулевая матрица, т.е.
Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например, .
Частный случай: произведение матрицы на число 0 есть нулевая матрица, т.е.
Слайд 152) Сложение матриц
Определение. Суммой матриц А и В одинакового размера называется
матрица
С = А + В, элементы которой равны суммам элементов матриц А и В, расположенных на соответствующих местах, т.е. матрицы складываются поэлементно:
для
для
Слайд 173) Вычитание матриц
Определение. Разность двух матриц одинакового размера определяется через предыдущие
операции:
А – В = А + (−1) ∙ В.
Например,
А – В = А + (−1) ∙ В.
Например,
Слайд 184) Умножение матриц.
Матрицу А можно умножить на матрицу В только в
том случае, когда число столбцов матрицы А равно числу строк матрицы В.
В результате умножения получится матрица С, у которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В, т.е.
В результате умножения получится матрица С, у которой столько же строк, сколько их в матрице А, и столько же столбцов, сколько их в матрице В, т.е.
Слайд 20Элементы матрицы С вычисляются по формуле:
,
т.е. каждый элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Правило. Для получения элемента , надо элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить .
т.е. каждый элемент равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Правило. Для получения элемента , надо элементы i-й строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить .
Слайд 225) Возведение в степень
Определение. Целой положительной степенью Ат (т>1) только квадратной
матрицы А называется произведение т матриц, равных А, т.е.
По определению:
По определению:
Слайд 246) Транспонирование матрицы -
переход от матрицы А к матрице
, в которой строки и столбцы поменялись местами с сохранением порядка.
Матрица называется транспонированной относительно матрицы А:
Матрица называется транспонированной относительно матрицы А:
Слайд 264. Свойства операций над матрицами
Многие свойства, присущие операциям над
числами, справедливы и для операций над матрицами:
А + В = В + А
(А + В) + С = А + (В + С)
А (В + С) = АВ +АС
(А + В) С = АС + ВС
А (В ∙ С) = (АВ) ∙ С
А + О = А
А – А = О
А + В = В + А
(А + В) + С = А + (В + С)
А (В + С) = АВ +АС
(А + В) С = АС + ВС
А (В ∙ С) = (АВ) ∙ С
А + О = А
А – А = О
Слайд 27Однако имеются и специфические свойства матриц.
Если произведение матриц А·В существует, то
после перестановки сомножителей местами произведение матриц В·А может и не существовать.
Например, существует,
а не существует.
Например, существует,
а не существует.
Слайд 282) Если даже произведения А·В и В·А существуют, то
они могут быть матрицами разных размеров.
Пример. Найти произведение матриц А·В и В·А :
Пример. Найти произведение матриц А·В и В·А :
Слайд 293) Когда оба произведения А·В и В·А существуют и оба
– матрицы одинакового размера, коммутативный (переместительный) закон умножения, вообще, не выполняется, т.е. .
Пример. Найти произведение матриц А·В и В·А , где
Решение.
Пример. Найти произведение матриц А·В и В·А , где
Решение.
Слайд 30Частный случай. Коммутативным законом обладает произведение любой квадратной матрицы А п-го
порядка на единичную матрицу того же порядка, причем это произведение равно А:
Т.о., единичная матрица при умножении играет ту же роль, что и число 1 при умножении чисел.
Т.о., единичная матрица при умножении играет ту же роль, что и число 1 при умножении чисел.
Слайд 314) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. из
того, что А·В = О, не следует, что А=О или В=О.
Например,
Например,
