- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие статистической взаимосвязи. (Тема 5) презентация
Содержание
- 1. Понятие статистической взаимосвязи. (Тема 5)
- 2. Цель лекции: Сформировать у обучаемых систему
- 3. ПЛАН ЛЕКЦИИ 1. Виды зависимостей между величинами
- 4. Все количественные характеристики объектов в математике обычно
- 5. Величины могут быть зависимыми и независимыми.
- 6. Существует два вида зависимостей: функциональная; стохастическая
- 7. Определение Зависимость между двумя величинами
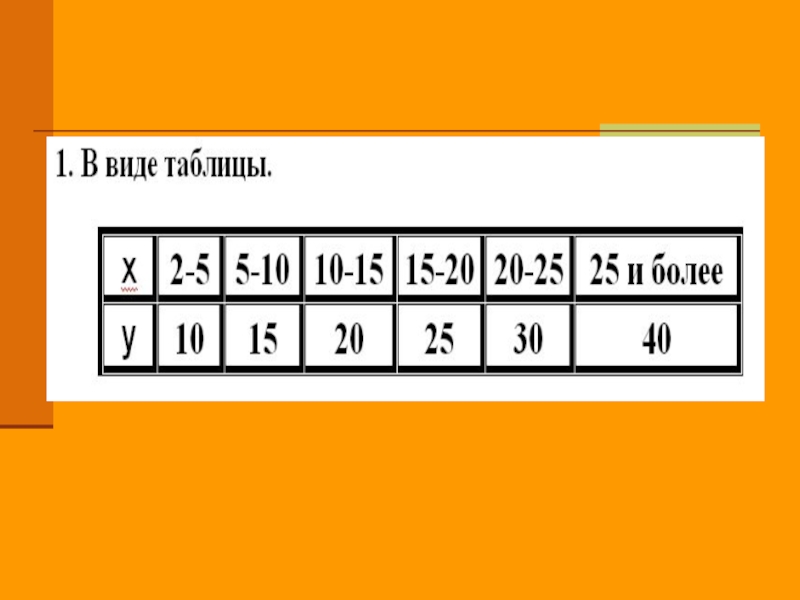
- 8. Пример Рассмотрим две величины х − выслуга
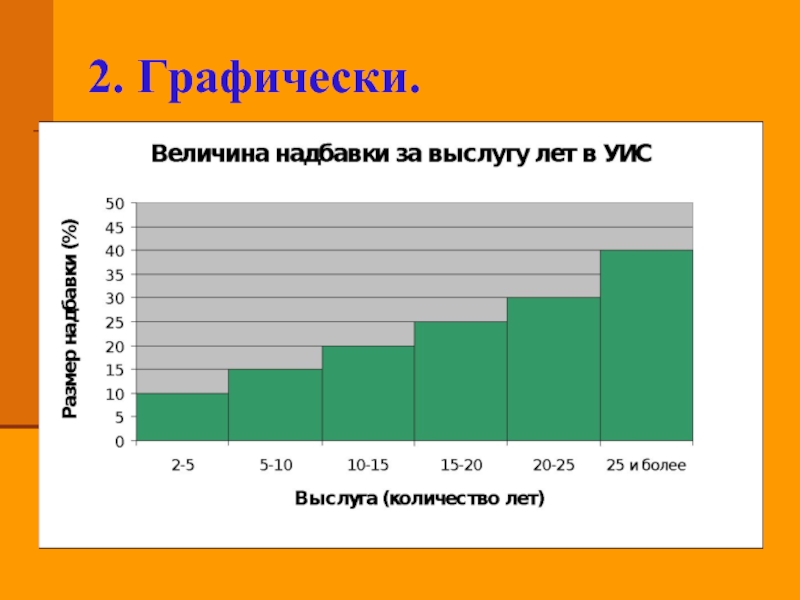
- 10. 2. Графически.
- 11. 3. Аналитически.
- 12. Определение Зависимость между двумя величинами
- 13. Y=f(X)+ε, где Y − значение результативного
- 14. 2. Корреляционный анализ Понятия корреляция и регрессия
- 15. Определение Корреляционная зависимость (или просто корреляция)
- 16. Виды корреляции Парная корреляция – связь между
- 17. Основные задачи корреляционного анализа определение существования и
- 18. Коэффициент корреляции
- 22. Использование MS Excel Для вычисления коэффициента корреляции
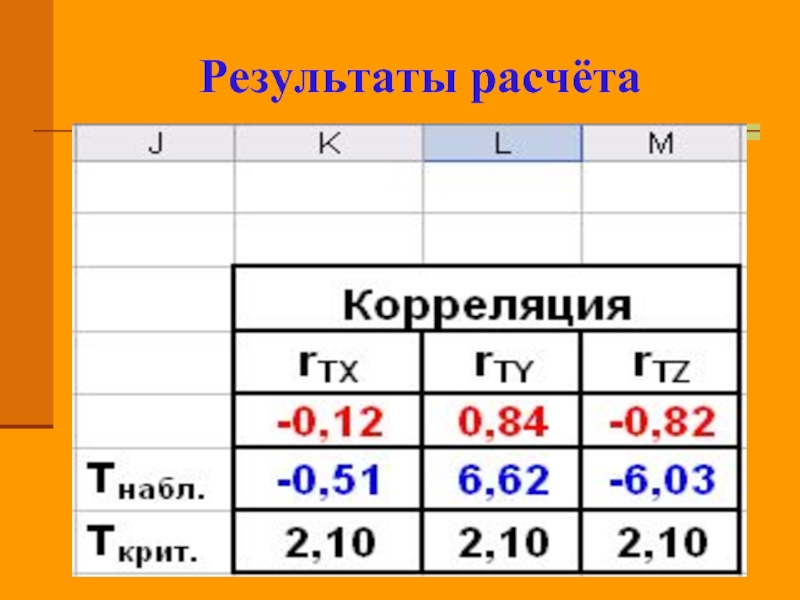
- 23. Результаты расчёта
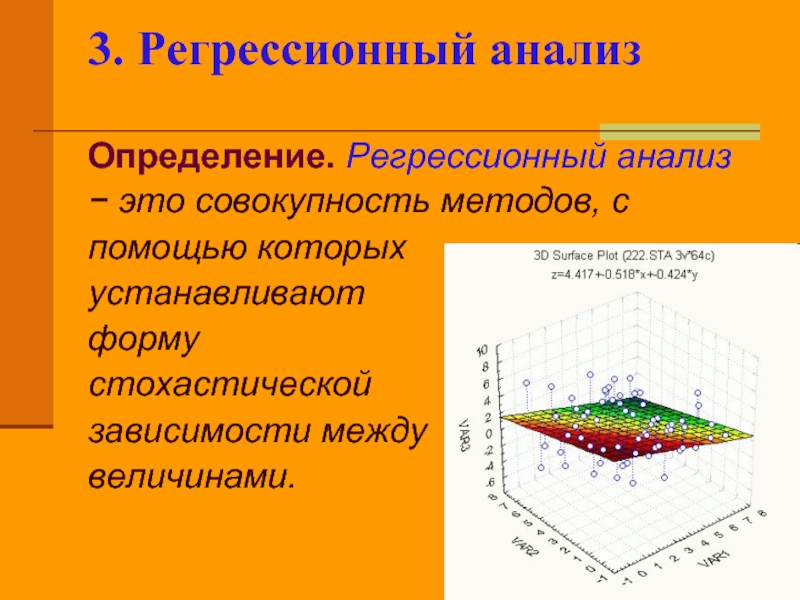
- 24. 3. Регрессионный анализ Определение. Регрессионный анализ
- 25. Пример На рабочем листе в диапазон ячеек
- 26. Алгоритм решения Для графического определения вида формы
- 28. Алгоритм решения Найдём значения параметров регрессии. Для
- 29. Алгоритм решения
- 30. Алгоритм решения Среди появившихся итогов находим коэффициенты
- 32. Проверка значимости модели регрессии с помощью критерия
- 33. Проверка значимости модели регрессии с помощью критерия Фишера 2. Вычисляют остаточную дисперсию.
- 34. Проверка значимости модели регрессии с помощью критерия
- 35. Проверка значимости модели регрессии с помощью критерия Фишера 4. Задают уровень значимости α: 0,01< α
- 36. Проверка значимости модели регрессии с помощью критерия
- 37. Проверка значимости модели регрессии с помощью критерия
- 38. 4. Доверительный интервал Доверительным интервалом называется интервал,
- 39. В общем виде доверительный интервал имеет вид:
- 40. Доверительный интервал для генеральной средней (математического ожидания)
- 41. Алгоритм нахождения доверительного интервала для среднего значения
- 42. Использование MS Excel 3. Задают доверительную вероятность ᵝ 0,9< ᵝ
- 43. Задавайте вопросы
Слайд 2Цель лекции:
Сформировать у обучаемых систему знаний о сущности методов корреляционного
и регрессионного анализа, об их роли в исследовании социально-правовых процессов.
Слайд 3ПЛАН ЛЕКЦИИ
1. Виды зависимостей между величинами
2. Корреляционный анализ
3. Регрессионный анализ
4. Доверительный
интервал
Слайд 4Все количественные характеристики объектов в математике обычно называют математическими величинами или
просто величинами.
Величины могут быть постоянными (constant) и переменными (variable).
Величины могут быть постоянными (constant) и переменными (variable).
1. Виды зависимостей между величинами
Слайд 5Величины могут быть зависимыми
и независимыми.
Также величины разделяют на
детерминированные и
случайные.
Слайд 6Существует два вида зависимостей:
функциональная;
стохастическая (вероятностная, статистическая; от греч. stochastikos –
умеющий угадывать, предполагать, строить предположение).
Слайд 7Определение
Зависимость между
двумя величинами
называется функциональной, если
каждому значению одной величины
соответствует единственное
значение
другой величины.
Слайд 8Пример
Рассмотрим две величины х − выслуга сотрудника УИС (количество лет), y
− размер надбавки от оклада по должности (%). Известно, что y зависит от x функционально (т. е. y является функцией от x) и эту зависимость можно представить различными способами.
Слайд 12Определение
Зависимость между
двумя величинами
называется стохастической,
если каждому значению одной
величины
соответствует
множество значений
другой величины.
множество значений
другой величины.
Слайд 13Y=f(X)+ε,
где Y − значение результативного
признака, f(X) − часть результативного
признака, сформированного
под
воздействием факторного признака X,
ε − часть результативного признака,
возникшая вследствие влияния других
неучтенных факторов.
воздействием факторного признака X,
ε − часть результативного признака,
возникшая вследствие влияния других
неучтенных факторов.
Модель стохастической связи
Слайд 142. Корреляционный анализ
Понятия корреляция и регрессия появились в середине XIX в.
благодаря работам английских статистиков Ф. Гальтона и К. Пирсона.
Первый термин произошёл от латинского correlation (соотношение, взаимосвязь),
второй также от латинского regressio (движение назад).
Первый термин произошёл от латинского correlation (соотношение, взаимосвязь),
второй также от латинского regressio (движение назад).
Фрэнсис Гальтон (1822-1911)
Карл Пирсон (1857-1936)
Слайд 15Определение
Корреляционная зависимость
(или просто корреляция) – это
статистическая зависимость
между случайными величинами,
при
которой каждому
значению одной величины соответствует
определённое значение условного
математического ожидания
(среднего значения) другой.
значению одной величины соответствует
определённое значение условного
математического ожидания
(среднего значения) другой.
Слайд 16Виды корреляции
Парная корреляция – связь между двумя признаками.
Частная корреляция – зависимость
между результативным и одним факторным признаками при фиксированном значении других факторных признаков.
Множественная корреляция – зависимость результативного признака и двух или более факторных признаков.
Множественная корреляция – зависимость результативного признака и двух или более факторных признаков.
Слайд 17Основные задачи корреляционного анализа
определение существования и тесноты корреляционной связи;
установление
достоверности
суждения о наличии
этой связи.
суждения о наличии
этой связи.
Слайд 22Использование MS Excel
Для вычисления коэффициента корреляции
используется стандартная функция
=КОРРЕЛ(Массив 1; Массив 2).
Для
вычисления критического значения
распределения Стьюдента используется
функция
=СТЬЮДРАСПОБР(p; n-2).
распределения Стьюдента используется
функция
=СТЬЮДРАСПОБР(p; n-2).
Слайд 243. Регрессионный анализ
Определение. Регрессионный анализ
− это совокупность методов, с
помощью которых
устанавливают
форму
стохастической
зависимости между
величинами.
Слайд 25Пример
На рабочем листе в диапазон ячеек B3:B17 введём значения величины X,
а в диапазон ячеек C3:C17 − величины Y.
Вычислим выборочный коэффициент корреляции RXY с помощью стандартной функции =КОРРЕЛ(B3:B17;C3:C17). В результате получаем RXY=0,98. Так как коэффициент корреляции близок к 1, то между признаками наблюдается тесная связь, близкая к линейной.
Вычислим выборочный коэффициент корреляции RXY с помощью стандартной функции =КОРРЕЛ(B3:B17;C3:C17). В результате получаем RXY=0,98. Так как коэффициент корреляции близок к 1, то между признаками наблюдается тесная связь, близкая к линейной.
Слайд 26Алгоритм решения
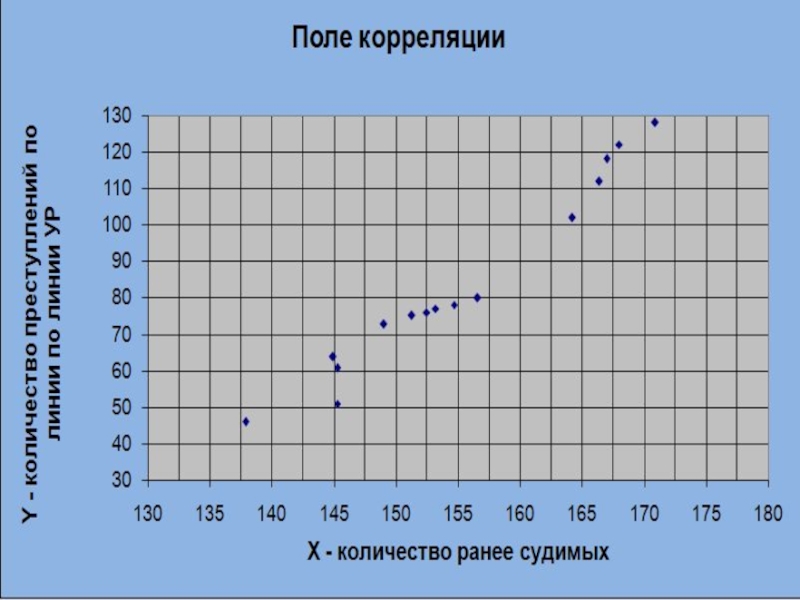
Для графического определения вида формы связи построим корреляционное поле, используя
стандартную точечную диаграмму. Расположение точек на корреляционном поле подтверждает сделанную выше гипотезу о линейной зависимости между Х и Y. Тогда функция регрессии имеет вид yx=a+bx.
Слайд 28Алгоритм решения
Найдём значения параметров регрессии. Для этого используем инструмент Сервис→Анализ данных→Регрессия.
В появившемся диалоговом окне «Регрессия» указываем диапазоны входных данных для X и Y, а также в выходном интервале указываем ссылку на левую верхнюю ячейку выходного диапазона для вывода итогов. Затем кнопка OK.
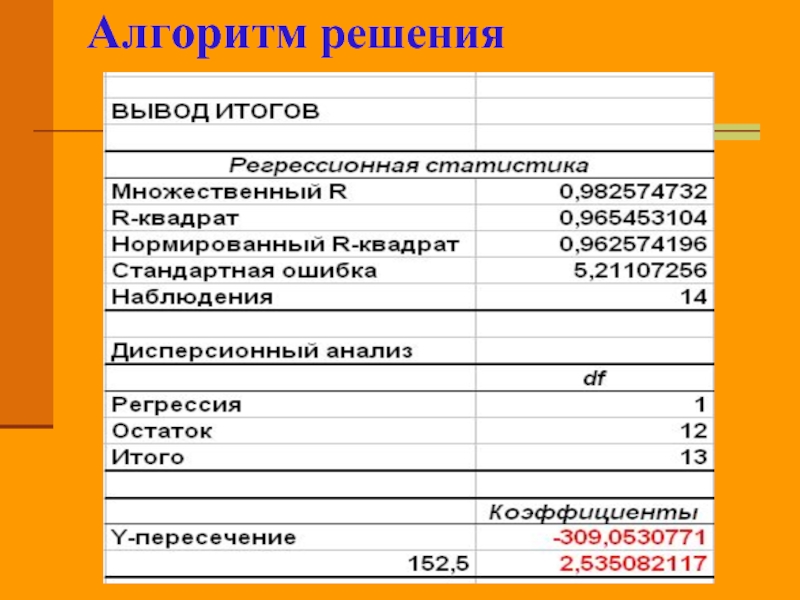
Слайд 30Алгоритм решения
Среди появившихся итогов находим коэффициенты регрессии b=2,54 и a=-309. Тогда
уравнение регрессии yx=-309+2,54x.
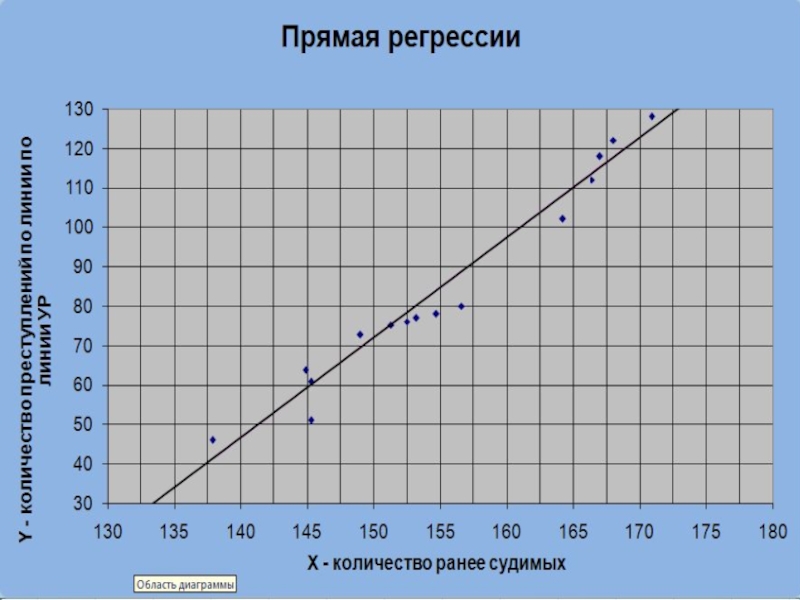
На корреляционном поле построим прямую y=-309+2,54x. Видно, что выборочные значения располагаются достаточно близко от этой прямой. Следовательно, полученная модель в некоторых случаях может быть использована для прогнозирования
На корреляционном поле построим прямую y=-309+2,54x. Видно, что выборочные значения располагаются достаточно близко от этой прямой. Следовательно, полученная модель в некоторых случаях может быть использована для прогнозирования
Слайд 32Проверка значимости модели регрессии с помощью критерия Фишера
(Алгоритм)
1. Вычисляют факторную дисперсию.
Слайд 33Проверка значимости модели регрессии с помощью критерия Фишера
2. Вычисляют остаточную дисперсию.
Слайд 34Проверка значимости модели регрессии с помощью критерия Фишера
3. Вычисляют наблюдаемое значение
критерия Фишера.
Слайд 35Проверка значимости модели регрессии с помощью критерия Фишера
4. Задают уровень значимости
α:
0,01< α<0,1.
0,01< α<0,1.
Слайд 36Проверка значимости модели регрессии с помощью критерия Фишера
5. C помощью стандартной
функции MS Excel находят теоретическое значение критерия Фишера Fтеор.
=F.ОБР(1- α;m;n-m-1)
=F.ОБР(1- α;m;n-m-1)
Слайд 37Проверка значимости модели регрессии с помощью критерия Фишера
6. Делают вывод.
Если Fфакт
> Fтеор, то модель регрессии признаётся статистически значимой в целом, и может быть использована для прогнозирования.
Слайд 384. Доверительный интервал
Доверительным интервалом называется интервал, который с заданной надёжностью (или
доверительной вероятностью) ᵝ покрывает оцениваемый параметр.
Слайд 41Алгоритм нахождения доверительного интервала для среднего значения
1. Для вычисления
выборочного среднего значения используется стандартная функция
=СРЗНАЧ(Массив)
2. Для вычисления выборочного среднего квадратического отклонения Sx используют функцию
=СТАНДОТКЛОН.В(Массив)
=СРЗНАЧ(Массив)
2. Для вычисления выборочного среднего квадратического отклонения Sx используют функцию
=СТАНДОТКЛОН.В(Массив)
Слайд 42Использование MS Excel
3. Задают доверительную вероятность ᵝ
0,9< ᵝ
4. Для вычисления допустимой предельной ошибки Δ используется функция
=ДОВЕРИТ.СТЬЮДЕНТ(1- ᵝ ;Sx;n)
=ДОВЕРИТ.СТЬЮДЕНТ(1- ᵝ ;Sx;n)