- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие множества презентация
Содержание
- 1. Понятие множества
- 2. Финансовый университет при Правительстве Российской Федерации Тема №1. Понятие множества
- 3. Множеством можно назвать совокупность объектов, связанных между
- 4. Объекты, входящие в это множество называются элементами
- 5. Часть элементов некоторого множества называется его подмножеством.
- 6. Пример
- 7. Множества Объединением двух множеств называется такое множество,
- 8. Множества Пересечением двух множеств называется такое множество,
- 9. Множества Примеры (диаграммы Эйлера-Венна):
- 10. Множества Разностью двух множеств называется такое множество,
- 11. Пример
- 12. Множества, элементами которых являются действительные числа, называются числовыми.
- 13. Геометрически множество действительных чисел изображается точками
- 14. Поэтому, в нашем случае понятия «число» и «точка» являются эквивалентными.
- 15. Множества Множество, содержащее все числа от
- 16. Множества Окрестностью точки множества А
- 17. Множества
- 18. Множества Точка, входящая
- 19. Множества Множество, каждая точка
- 20. Множества Пусть есть
- 21. Множества Пусть множество ограничено сверху.
- 22. Множества Наименьшая из всех верхних
- 23. Модуль Абсолютной величиной (или модулем) числа х
- 24. Множества Символика:
- 25. Финансовый университет при Правительстве Российской Федерации Тема №2. Понятие функции. Основные свойства функций.
- 26. Функции
- 27. Множество Х называется областью определения функции
- 28. Задача Пример№1. Найти ООФ
- 29. Задача Решение: Вспомним ограничения, накладываемые на некоторые
- 30. Задача Таким образом имеем следующую систему неравенств:
- 31. Задать функцию означает задать её
- 32. Основными способами задания функции являются: Аналитический
- 33. Функция называется чётной, если для любых значений
- 34. Задача Например, функция
- 35. График чётной функции симметричен относительно оси ординат.
- 36. Функция называется возрастающей на множестве, если большему
- 37. Функции Если для любого х из ООФ
- 38. Пример Функция
- 39. Функции Функция называется периодической с периодом Т
- 40. Пример Функции
- 41. Основные элементарные функции
- 42. Основные элементарные функции 2. Линейная функция. (Рассмотрена
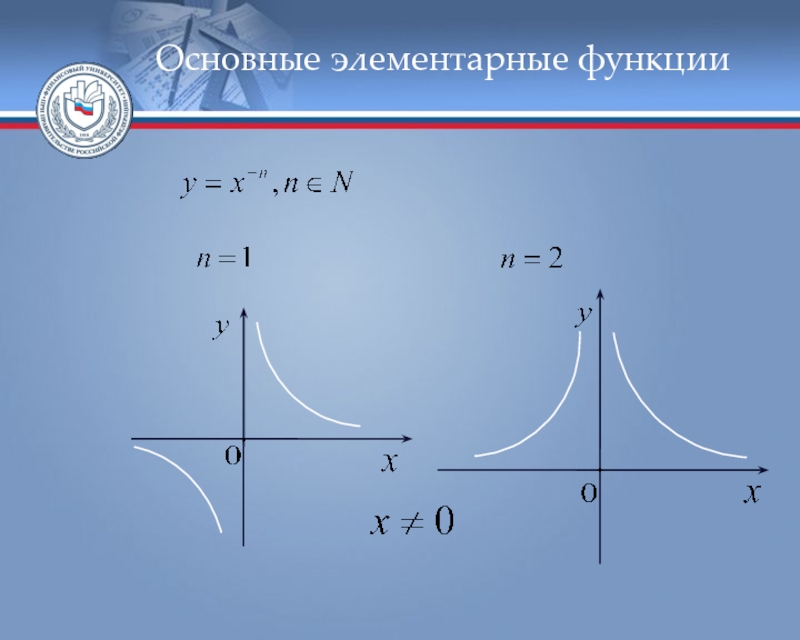
- 43. Основные элементарные функции
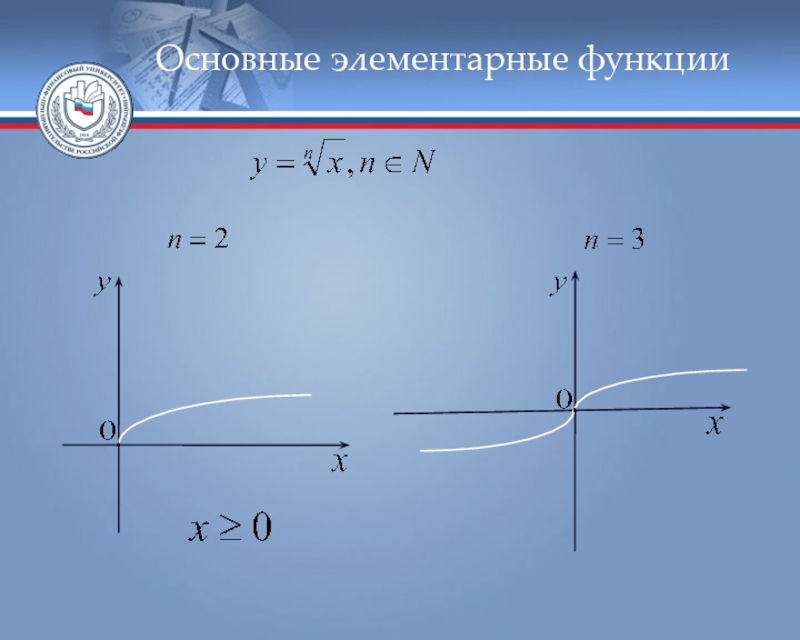
- 44. Основные элементарные функции
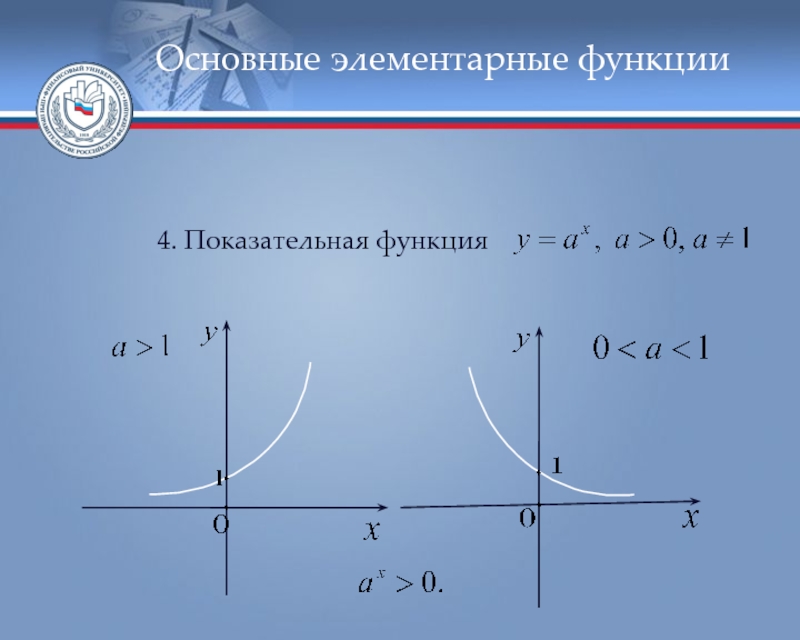
- 45. Основные элементарные функции 4. Показательная функция
- 46. Основные элементарные функции 5. Логарифмическая функция:
- 47. Задача
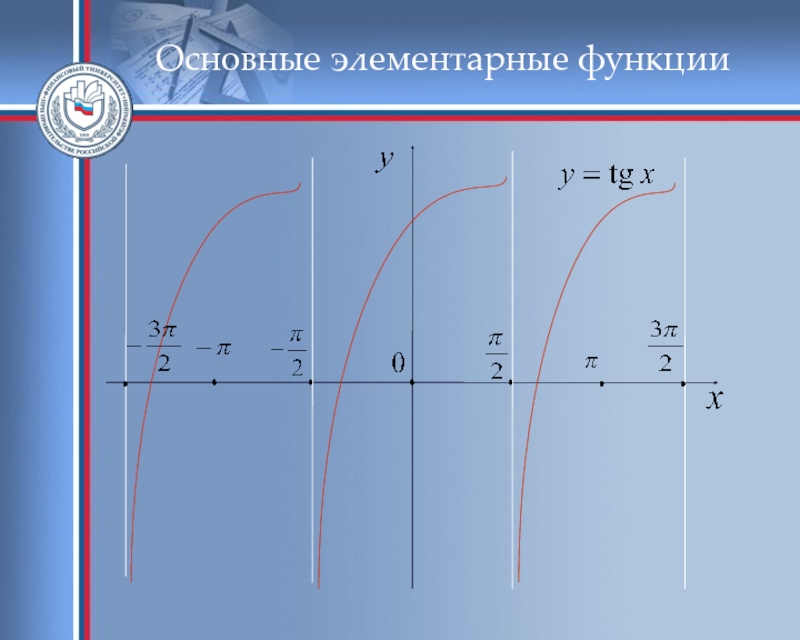
- 48. Основные элементарные функции 6. Тригонометрические функции:
- 49. Основные элементарные функции
- 50. Основные элементарные функции
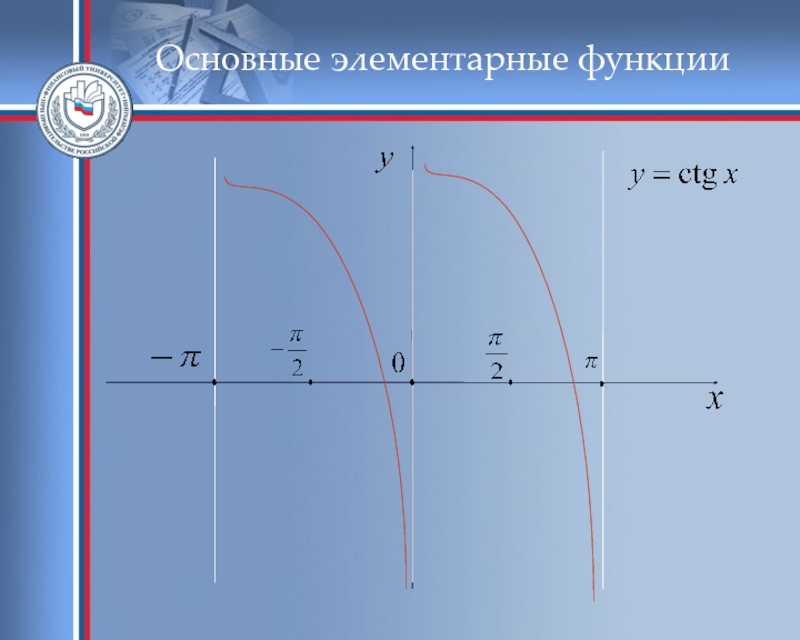
- 51. Основные элементарные функции
- 52. Основные элементарные функции
- 53. Основные элементарные функции 7. Обратные тригонометрические функции:
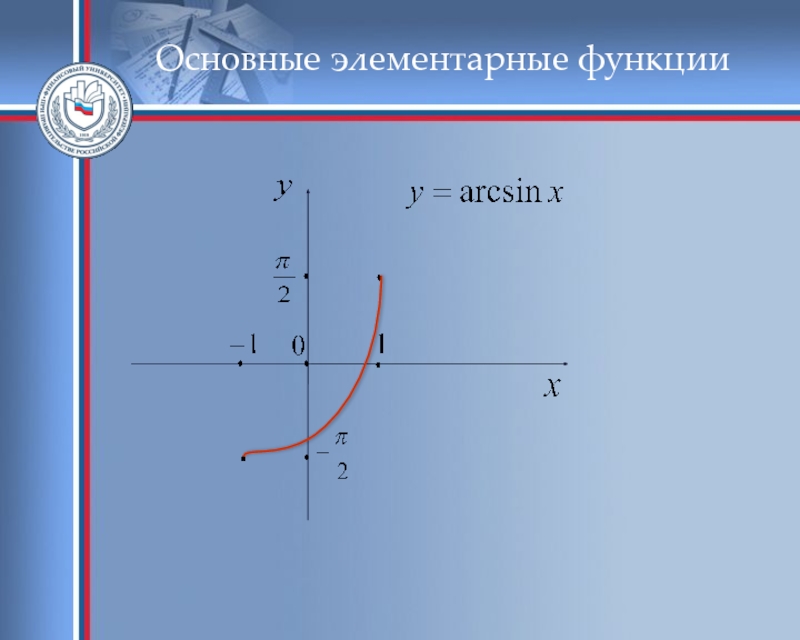
- 54. Основные элементарные функции
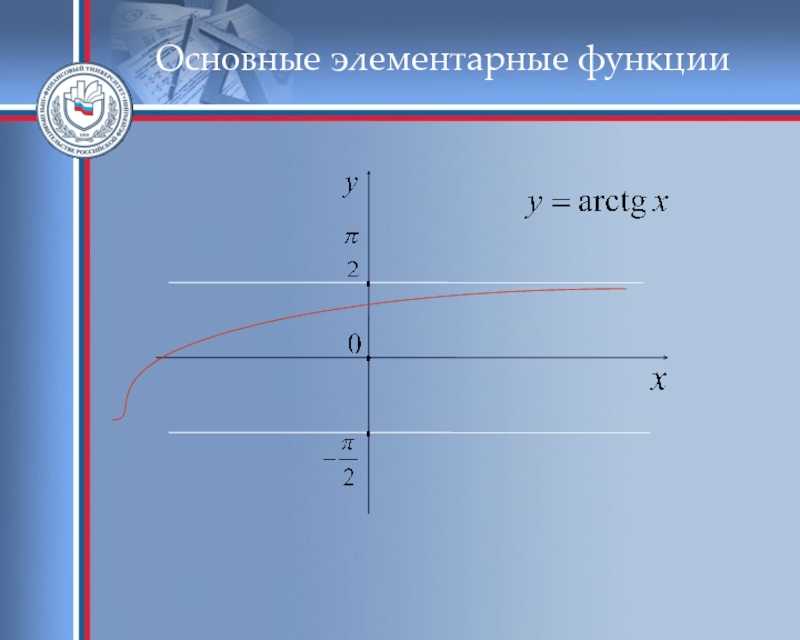
- 55. Основные элементарные функции
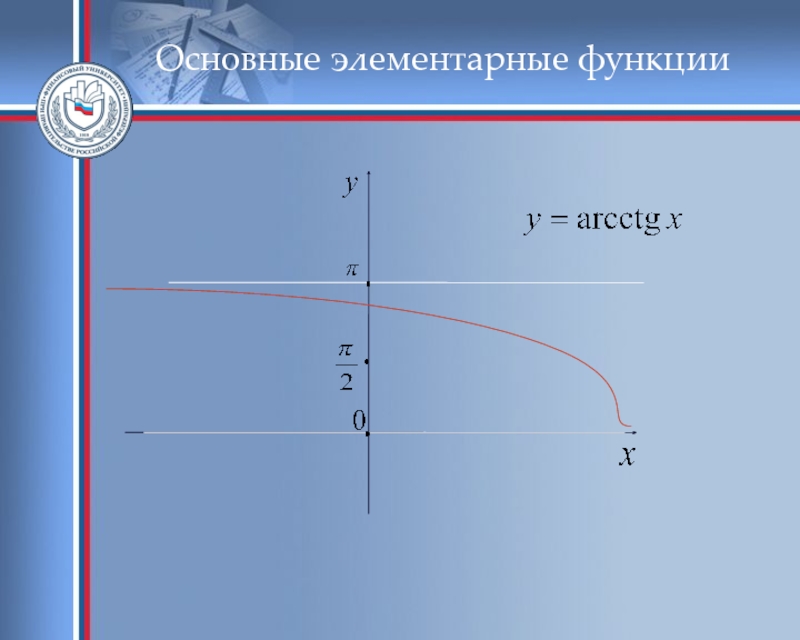
- 56. Основные элементарные функции
- 57. Основные элементарные функции
- 58. Функции Функции, составленные (построенные) из основных
- 59. Функции Функция y, значения которой
- 60. Функции Пусть задана функция
- 61. Задача Например, обратной к показательной
- 62. Преобразования графиков:
- 63. График функции
- 64. Финансовый университет при Правительстве Российской Федерации Тема №3. Пределы и непрерывность
- 65. Последовательность Если в имеющейся функциональной зависимости независимая
- 66. Последовательность Примерами числовых последовательностей являются арифметическая и геометрическая прогрессии.
- 67. Последовательность Основными способами задания
- 68. Число A называется пределом числовой
- 69. Последовательности
- 70. Задача Проиллюстрируем, что
- 71. Задача
- 72. Признаки существования предела Если
- 73. Признаки существования предела ТЕОРЕМА
- 74. Признаки существования предела Эти
- 75. Последовательность Последовательность
- 76. Последовательность Одним из критериев
- 77. Число А называется пределом функции при х
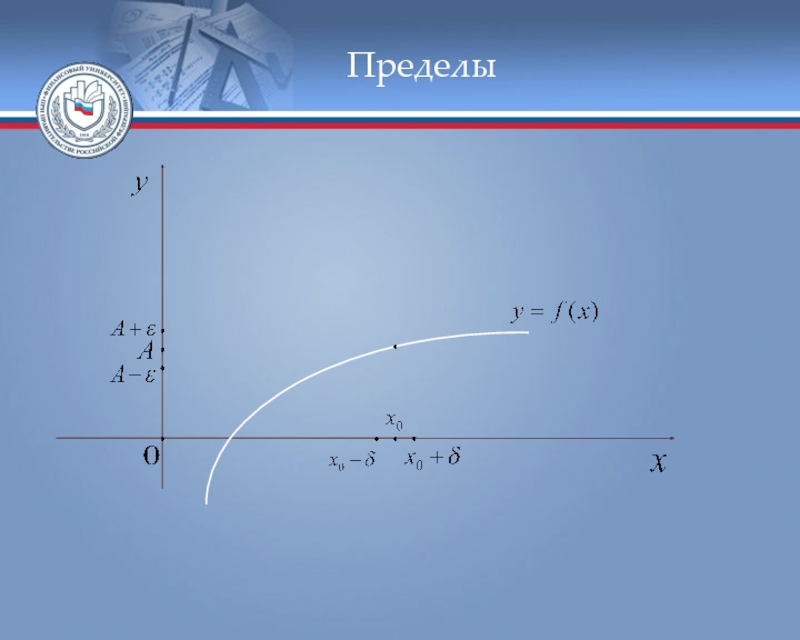
- 78. Определение предела функции в точке.
- 79. Пределы
- 80. Основные теоремы о пределах Функция не может
- 81. Основные теоремы о пределах Предел частного двух
- 82. Основные теоремы о пределах 7.Теорема
- 83. Пределы Если
- 84. Задача Например, функция
- 85. Свойства бесконечно малых и бесконечно больших
- 86. Произведение бесконечно малой на ограниченную функцию является
- 87. Произведение бесконечно большой на функцию, предел которой
- 88. Замечательные пределы 1. 2.
- 89. Пусть
- 90. При этом, если С=1,
- 91. Число e – число
- 93. В условиях
- 94. S – наращенная сумма,
- 95. Чтобы найти предел элементарной функции, когда
- 96. Задача Пример. Найти:
- 97. Задача Решение:
- 98. Пределы Некоторые виды неопределённостей:
- 99. Задача Пример. Найти:
- 100. Задача Решение:
- 101. Пределы 1-й тип: Пределы вида Следует
- 102. Задача Пример. Найти:
- 103. Задача Решение:
- 104. Задача Пример. Найти:
- 105. Задача Решение:
- 106. Задача Пример. Найти:
- 107. Задача Решение:
- 108. Задача Пример. Найти:
- 109. Задача Решение:
- 110. Задача Пример. Найти:
- 111. Задача Решение: a) b)
- 112. Пределы 2-й тип: Пределы вида Следует
- 113. Задача Пример. Найти:
- 114. Задача
- 115. Задача Решение:
- 116. Задача Пример. Найти:
- 117. Задача Решение:
- 118. Пределы 3-й тип: Неопределённость устраняется или
- 119. Задача Пример. Найти:
- 120. Задача Решение:
- 121. Задача Пример. Найти:
- 122. Задача Решение:
- 123. Задача
- 124. Пределы 4-й тип. Решается при помощи выделения «второго замечательного предела».
- 125. Задача Пример. Найти:
- 126. Задача Решение:
- 127. Задача Пример. Найти:
- 128. Задача Решение:
- 129. Пределы 5-й тип. Выделение «первого замечательного предела».
- 130. Задача Пример. Найти:
- 131. Задача Решение:
- 132. Задача Пример. Найти:
- 133. Задача Решение:
- 134. Задача Или:
- 135. Функция называется непрерывной в точке, если она
- 136. Свойства функций, непрерывных в точке:
- 137. Если функция непрерывна и положительна в некоторой
- 138. Свойства функций, непрерывных в точке:
- 139. Свойства функций, непрерывных на отрезке:
- 140. Если функция непрерывна на отрезке и значения
- 141. Классификация точек разрыва функции:
- 142. 2. Разрыв 1-го рода неустранимый: оба
- 143. 3. Устранимый разрыв (1-го рода): односторонние пределы
- 144. Асимптотой графика функции называется
- 145. Вертикальные асимптоты проходят через
- 146. Наклонные асимптоты ищутся в виде:
- 147. Финансовый университет при Правительстве Российской Федерации Конец презентации
Слайд 3 Множеством можно назвать совокупность объектов, связанных между собой общими признаками.
Обозначаются множества
Слайд 4 Объекты, входящие в это множество называются элементами данного множества.
Обозначаются элементы маленькими
- элемент из множества
Элементы множества
Слайд 5 Часть элементов некоторого множества называется его подмножеством.
Обозначается так же, как и
- множество является подмножеством множества .
Подмножество
Слайд 6Пример
Множество натуральных
Множество целых чисел
Множество рациональных чисел
Множество действительных чисел
Слайд 7Множества
Объединением двух множеств называется такое множество, которое состоит из элементов, каждый
Слайд 8Множества
Пересечением двух множеств называется такое множество, которое состоит из элементов, одновременно
Слайд 10Множества
Разностью двух множеств называется такое множество, которое состоит из элементов уменьшаемого
Слайд 13 Геометрически множество действительных чисел изображается точками на числовой прямой (оси
и прямой установлено взаимно однозначное соответствие, т.е. каждому действительному
числу соответствует одна единственная точка
на числовой прямой, и наоборот, любой точке числовой прямой соответствует одно единственное действительное число.
Слайд 15Множества
Множество, содержащее все числа
от a до b включительно, называют отрезком
Множество, содержащее все числа между a и b, называют интервалом, (a; b).
(a; b], [a; b) – полуинтервалы.
Слайд 16Множества
Окрестностью точки множества А называется такое подмножество множества А,
Слайд 17Множества
Если из этого подмножества
Слайд 18Множества
Точка, входящая в данное множество вместе с
Если у точки множества имеется окрестность, не пересекающаяся с данным множеством, то такая точка называется изолированной точкой множества.
Точка, в любой окрестности которой содержится по крайней мере одна точка данного множества, отличная от неё самой, называется предельной точкой множества.
Слайд 19Множества
Множество, каждая точка которого входит в него вместе
Множество, содержащее все свои предельные точки называется замкнутым.
Слайд 20Множества
Пусть есть некоторое множество точек на прямой.
Слайд 21Множества
Пусть множество ограничено сверху. Тогда на прямой существуют точки,
Слайд 22Множества
Наименьшая из всех верхних граней называется супремумом (sup X).
Непустое множество, ограниченное сверху имеет верхнюю грань; ограниченное снизу имеет нижнюю грань.
Слайд 23Модуль
Абсолютной величиной (или модулем) числа х называют само число х, если
по знаку число –х, если оно отрицательно.
Слайд 25Финансовый университет
при Правительстве Российской Федерации
Тема №2.
Понятие функции.
Основные свойства функций.
Слайд 27 Множество Х называется областью определения функции (в дальнейшем ООФ), а
Если ООФ заранее не оговорена, то
под ней понимается множество значений аргумента, при котором функция имеет смысл.
Будем рассматривать только те функции, у которых одному значению аргумента соответствует одно единственное значение функции.
Слайд 29Задача
Решение: Вспомним ограничения, накладываемые на некоторые выражения:
Знаменатель дроби отличен от нуля;
Выражение
Выражение под знаком логарифма должно быть положительным (строго больше нуля).
Для функций
Слайд 30Задача
Таким образом имеем следующую систему неравенств:
Данное множество является ответом нашей задачи.
Слайд 31 Задать функцию означает задать
её ООФ и правило, при помощи
Слайд 32Основными способами
задания функции являются:
Аналитический (формулой)
Табличный (таблицей соответствия между переменными)
Графический (графиком
Словесный (применяется редко для некоторых специальных функций)
Слайд 33 Функция называется чётной, если для любых значений х из ООФ справедливо
Функция называется нечётной, если для любых значений х из ООФ справедливо равенство
Если ни одно из двух равенств не выполнено, то функция является функцией общего вида.
Слайд 34Задача
Например, функция
Функция является нечётной, т.к.
Функция является функцией общего вида, т.к.
Слайд 35 График чётной функции симметричен относительно оси ординат.
График нечётной функции симметричен относительно
На графике функции общего вида отсутствуют указанные выше два вида симметрий.
Слайд 36 Функция называется возрастающей на множестве, если большему значению аргумента
из этого
Функция называется убывающей на множестве, если большему значению аргумента
из этого множества соответствует меньшее значение функции.
Возрастающие и убывающие функции являются монотонными. (К монотонным относятся также невозрастающие и неубывающие функции).
Слайд 37Функции
Если для любого х из ООФ справедливо неравенство
Если для любого х из ООФ справедливо неравенство , где m – некоторое постоянное число, то функция является ограниченной снизу на множестве.
Если функция на некотором множестве ограничена сверху и снизу, то она на этом множестве является ограниченной.
Слайд 38Пример
Функция
Функция является ограниченной снизу.
Функции являются ограниченными.
Слайд 39Функции
Функция называется периодической с периодом Т отличным от нуля, если для
причём в качестве периода принимается наименьшее среди таких значений Т.
Слайд 41Основные элементарные функции
Основными элементарными функциями являются следующие функции:
1. Постоянная
Слайд 58Функции
Функции, составленные (построенные)
из основных элементарных функций при помощи конечного числа
Слайд 59Функции
Функция y, значения которой находятся из уравнения, разрешённого относительно
Функция y, значения которой находятся из уравнения, не разрешённого относительно y, называется неявной
Слайд 60Функции
Пусть задана функция
определённая на множестве Y, с областью значений X, называется обратной.
Обозначают:
Слайд 61Задача
Например, обратной к показательной функции
Графики взаимно обратных функций симметричны относительно биссектрисы 1-го и 3-го координатных углов.
Слайд 62Преобразования графиков:
График функции
График функции получается из графика функции сдвигом вдоль оси y (вверх, если a > 0, вниз, если a<0).
Слайд 63График функции
График функции получается из графика функции растяжением (при 0 < k < 1) или сжатием (при k > 1) вдоль оси x.
Преобразования графиков:
Слайд 64Финансовый университет
при Правительстве Российской Федерации
Тема №3.
Пределы и непрерывность
Слайд 65Последовательность
Если в имеющейся функциональной зависимости независимая переменная принимает только натуральные значения,
Слайд 66Последовательность
Примерами числовых последовательностей являются арифметическая и геометрическая прогрессии.
Слайд 67Последовательность
Основными способами задания числовых последовательностей являются рекуррентный (формула
Слайд 68 Число A называется пределом числовой последовательности
Слайд 72Признаки существования предела
Если числовая последовательность имеет конечный предел,
ТЕОРЕМА 1. Числовая последовательность может иметь только один предел (конечный или бесконечный).
Слайд 73Признаки существования предела
ТЕОРЕМА 2. Если последовательность имеет конечный
ТЕОРЕМА 3. Если , а ,
и , то .
ТЕОРЕМА 4. Если последовательности стремятся к одному и тому же пределу, равному a, и , то последовательность тоже стремится к числу a.
Слайд 75Последовательность
Последовательность называется бесконечно
Взаимосвязь между ними и свойства аналогичны бесконечно малым и бесконечно большим функциям (будут рассмотрены позже).
Слайд 76Последовательность
Одним из критериев существования предела является следующая Теорема:
Теорема Кантора (лемма о вложенных отрезках): Для всякой системы вложенных отрезков существует хотя бы одна точка, которая принадлежит всем отрезкам данной системы одновременно. Причём, если длина отрезков стремится к нулю, то упомянутая точка будет единственной.
Слайд 77 Число А называется пределом функции при х стремящемся к бесконечности, если
в области значений этой функции можно выделить такую последовательность, предел которой равен А. (Определение предела по Гейне).
Слайд 78 Определение предела функции в точке. Пусть функция
Число А называется пределом функции
в точке тогда и только тогда, когда для любой сколь угодно малой окрестности точки А найдётся зависящая от неё окрестность точки такая, что все точки из ООФ, лежащие внутри этой окрестности отобразятся в упомянутую окрестность точки А при помощи (Определение предела по Коши).
Слайд 80Основные теоремы о пределах
Функция не может иметь более одного предела (при
Предел алгебраической суммы конечного числа слагаемых равен алгебраической сумме пределов этих слагаемых;
Предел произведения конечного числа множителей равен произведению пределов этих множителей;
Слайд 81Основные теоремы о пределах
Предел частного двух функций равен частному пределов этих
Предел постоянной величины равен этой постоянной;
Постоянный множитель можно выносить за знак предела.
Слайд 82Основные теоремы о пределах
7.Теорема о пределе сложной функции:
Пусть
то существует
Слайд 83Пределы
Если
Если то называется бесконечно большой величиной при соответствующем стремлении х;
Слайд 84Задача
Например, функция является
бесконечно малой
Слайд 85Свойства бесконечно малых
и бесконечно больших величин:
1. Если бесконечно малая, то бесконечно большая при том же стремлении х (верно и обратное);
2. Алгебраическая сумма и произведение конечного числа бесконечно малых являются бесконечно малыми;
Слайд 86Произведение бесконечно малой на ограниченную функцию является бесконечно малой;
Частное от деления
Если функцию можно представить в виде суммы постоянной величины и бесконечно малой, то эта постоянная является пределом функции;
Свойства бесконечно малых
и бесконечно больших величин:
Слайд 87Произведение бесконечно большой на функцию, предел которой отличен от нуля является
Сумма бесконечно большой и ограниченной является бесконечно большой;
Частное от деления бесконечно большой на функцию, имеющую конечный предел является бесконечно большой.
Свойства бесконечно малых
и бесконечно больших величин:
Слайд 89 Пусть
Если , то имеет
больший порядок малости;
Если , то имеет больший порядок малости;
Если , то имеют один и тот же порядок малости.
Сравнение бесконечно малых :
Слайд 90 При этом, если С=1, то бесконечно малые являются
Примеры эквивалентных бесконечно малых величин при
Можно пользоваться при вычислении пределов функций.
Сравнение бесконечно малых :
Слайд 91 Число e – число Эйлера или число Непера.
Слайд 93 В условиях финансовой операции указывается не
Слайд 94 S – наращенная сумма, m – количество начислений
Слайд 95 Чтобы найти предел элементарной функции, когда аргумент стремится к значению,
Слайд 101Пределы
1-й тип: Пределы вида
Следует и в числителе, и в знаменателе дроби
Слайд 112Пределы
2-й тип: Пределы вида
Следует разложить на множители и числитель, и знаменатель
Слайд 118Пределы
3-й тип:
Неопределённость устраняется или приводится к предыдущим двум типам приведением к
Слайд 135 Функция называется непрерывной в точке, если она определена в этой точке
Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Слайд 136Свойства функций,
непрерывных в точке:
Сумма и произведение непрерывных функций
Частное двух функций является непрерывной функцией при условии, что делитель отличен от нуля;
Слайд 137Если функция непрерывна и положительна в некоторой точке, то найдётся такая
Если функция непрерывна в точке , а функция непрерывна в точке , причём то сложная функция непрерывна в точке
Свойства функций,
непрерывных в точке:
Слайд 138Свойства функций,
непрерывных в точке:
Этим 4-м свойством
5. Если функция непрерывна в некоторой точке, то найдётся такая её окрестность, в которой эта функция ограничена.
6. Если функция в некоторой точке определена и имеет конечный предел, отличный от нуля, то найдётся такая проколотая окрестность упомянутой точки, в которой функция имеет тот же знак, что и предел.
Слайд 139Свойства функций,
непрерывных на отрезке:
Если функция непрерывна на
Если функция непрерывна на отрезке, то она на этом отрезке достигает своих наибольшего и наименьшего значений (2-я теорема Вейерштрасса)
Функция обратная к непрерывной и монотонной является непрерывной
Слайд 140Если функция непрерывна на отрезке и значения функции на её концах
Функция, непрерывная на отрезке, внутри него хотя бы один раз принимает значение, заключённое между значениями функции на концах отрезка
Свойства функций,
непрерывных на отрезке:
Слайд 141Классификация точек разрыва функции:
1. Разрыв 2-го рода (неустранимый): хотя
Слайд 1422. Разрыв 1-го рода неустранимый: оба односторонних предела конечны, но
Классификация точек разрыва функции:
Слайд 1433. Устранимый разрыв (1-го рода): односторонние пределы конечны, равны между собой,
Классификация точек разрыва функции:














![Множества Множество, содержащее все числа от a до b включительно, называют отрезком (или сегментом), [a; b]. Множество,](/img/tmb/3/209654/b3b5a6028ca19af8cdf1e243c6264b7d-800x.jpg)