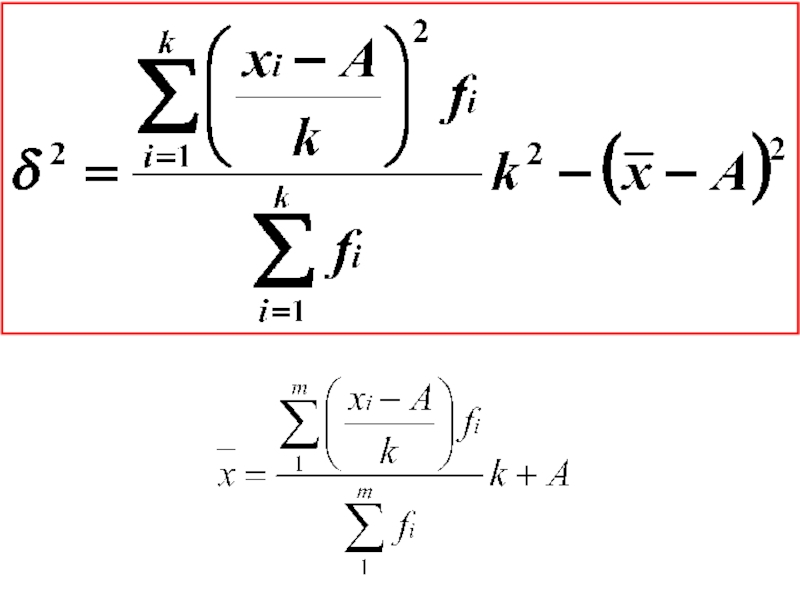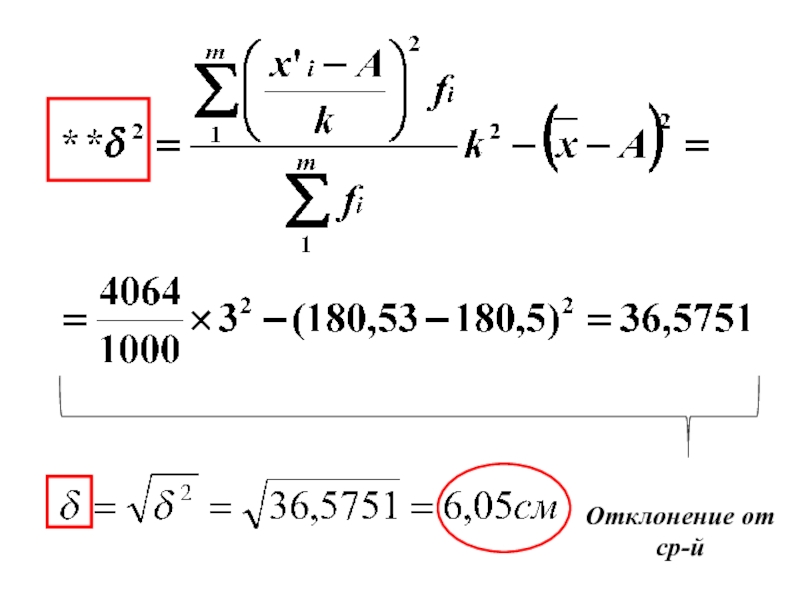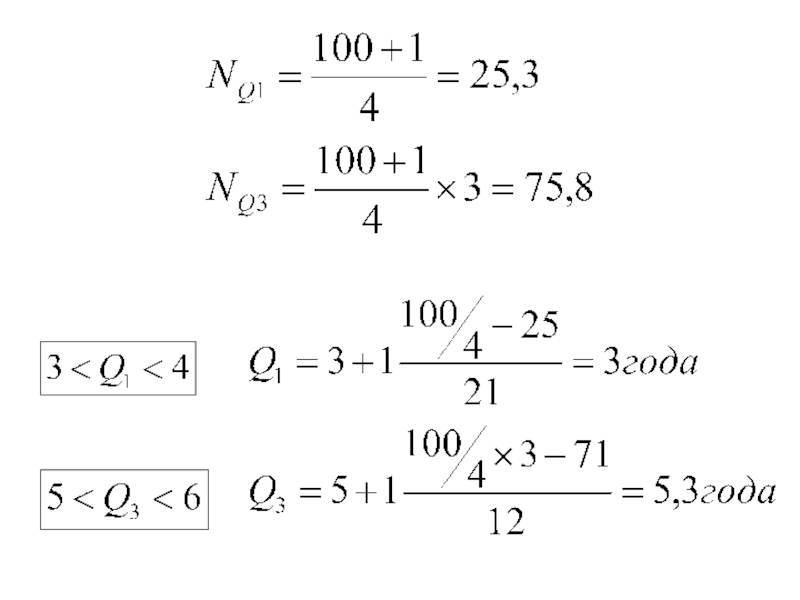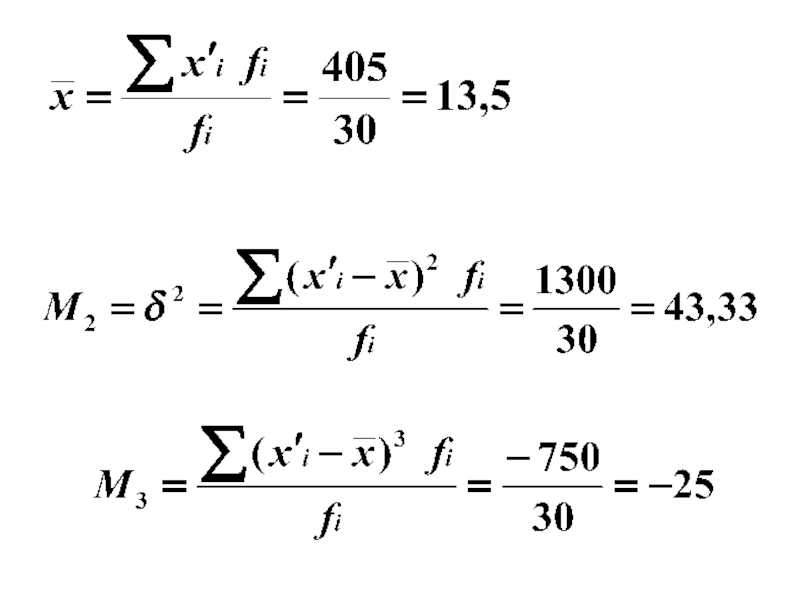- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показатели вариации и анализ частотных распределений презентация
Содержание
- 1. Показатели вариации и анализ частотных распределений
- 3. – соответственно нижняя граница и величина модального
- 5. Ширина интервала i=2
- 6. При нечетном числе вариантов: При четном числе вариантов:
- 7. 5, 4, 3, 4, 5, 5, 6,
- 8. 2, 3, 3, 3, 4, 4, 5,
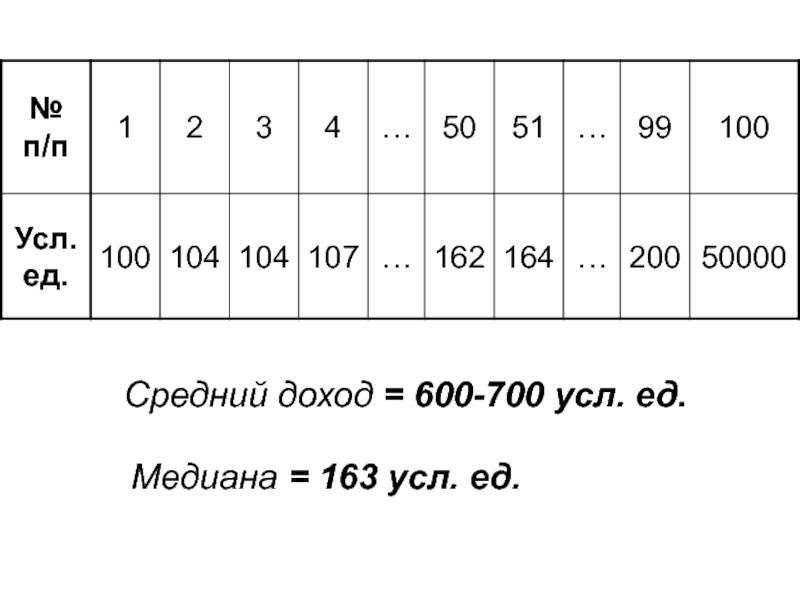
- 9. Средний доход = 600-700 усл. ед. Медиана = 163 усл. ед.
- 10. Где n – число единиц совокупности Положение медианы в ряду распределения:
- 11. – соответственно нижняя граница и величина медианного
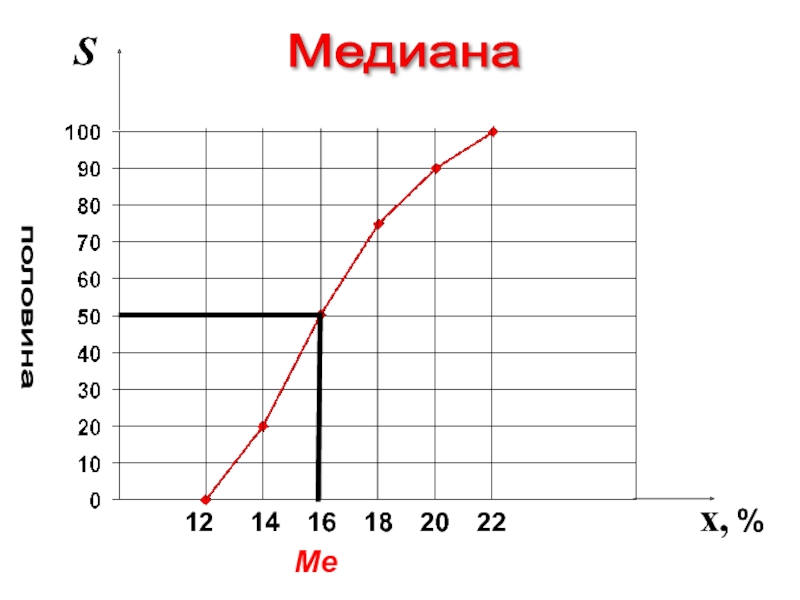
- 12. Пример: Интервал 16-18
- 13. В приведенном примере:
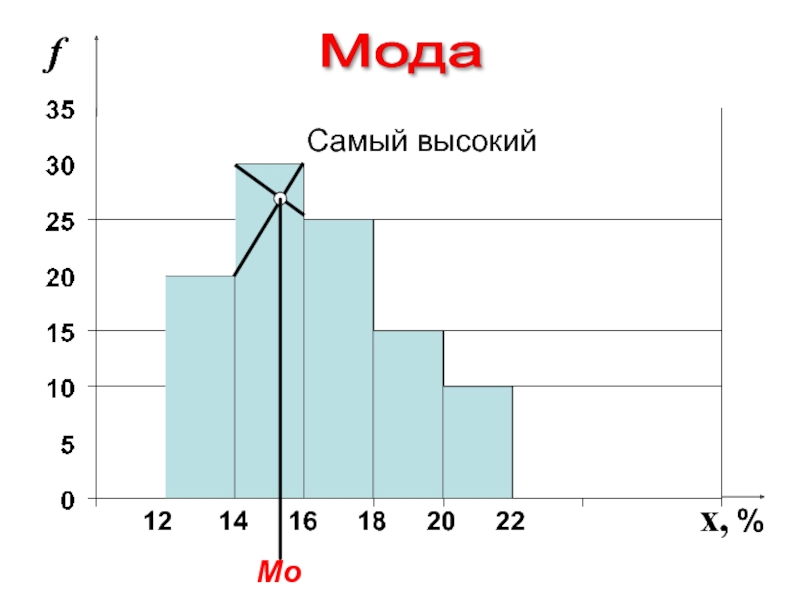
- 14. 12 14 16 18 20 22 x, % f Mo Самый высокий Мода
- 15. 12 14 16 18 20 22 x, % S Медиана половина Me
- 16. Вариационный размах
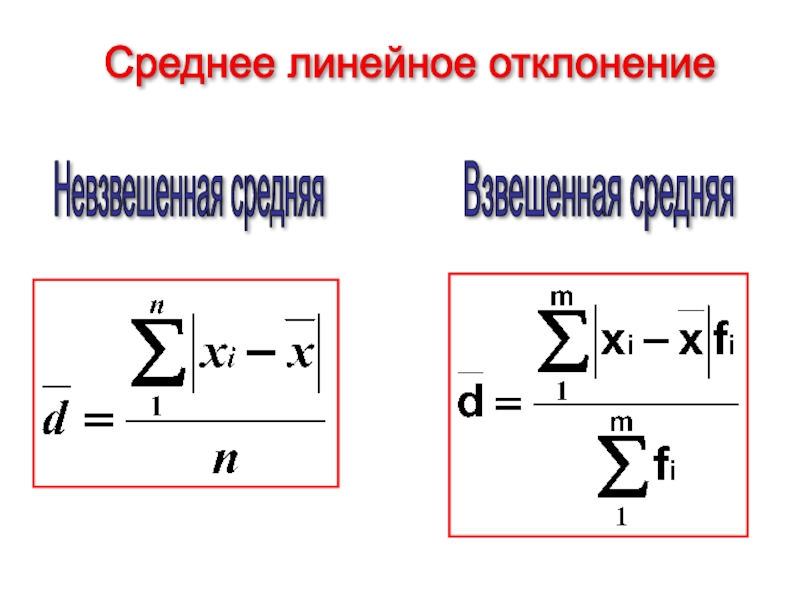
- 17. Среднее линейное отклонение Невзвешенная средняя Взвешенная средняя
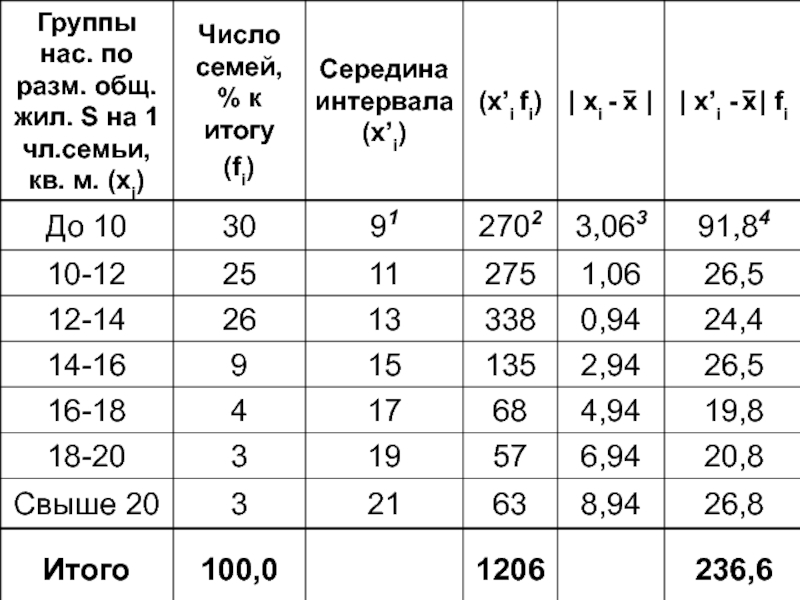
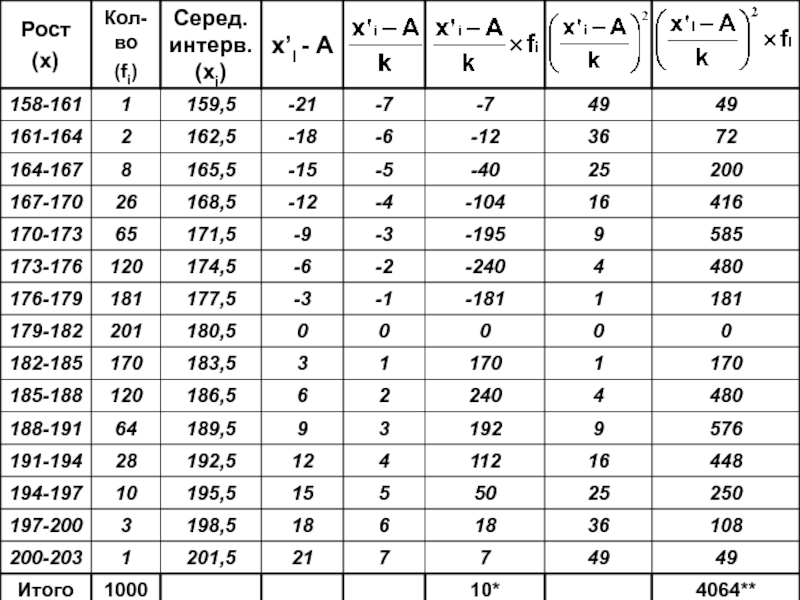
- 19. Алгоритм расчета 1) Найдем середину интервалов (x’i) До 10
- 20. Алгоритм расчета Рассчитаем среднюю величину по
- 21. Алгоритм расчета 3) Найдем абсолютные отклонения
- 22. Алгоритм расчета Сумму произведений делим на
- 23. Алгоритм расчета Совокупность в отношении признака однородна, средняя - типична Отличие от средней
- 24. Дисперсия Простая (невзвешенная) Взвешенная
- 25. Простое (невзвешенное) Взвешенное Среднее квадратическое отклонение
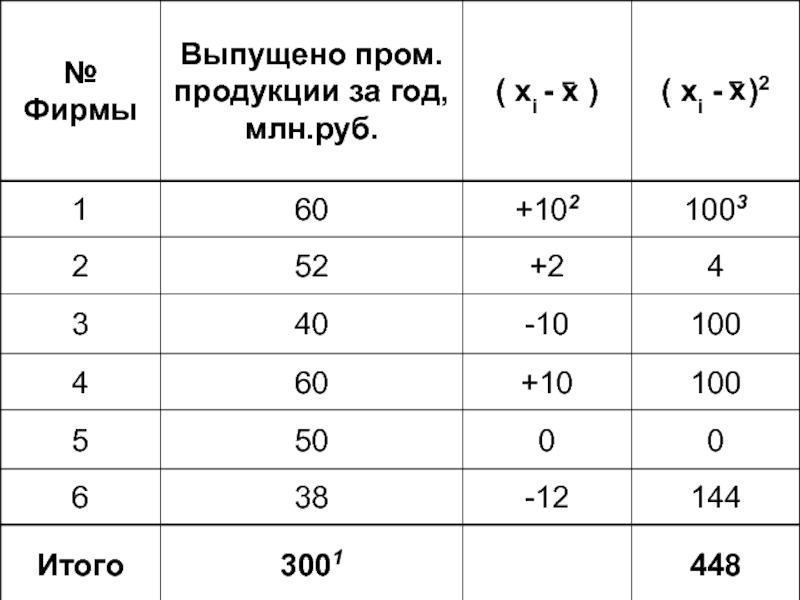
- 27. Алгоритм расчета 1) Определим среднюю величину
- 28. Алгоритм расчета 2) Найдем отклонения 3)
- 29. Алгоритм расчета 5) Извлечем из дисперсии
- 30. Относительные показатели вариации - коэффициент осцилляции - линейный коэффициент вариации или
- 31. Относительные показатели вариации - коэффициент вариации
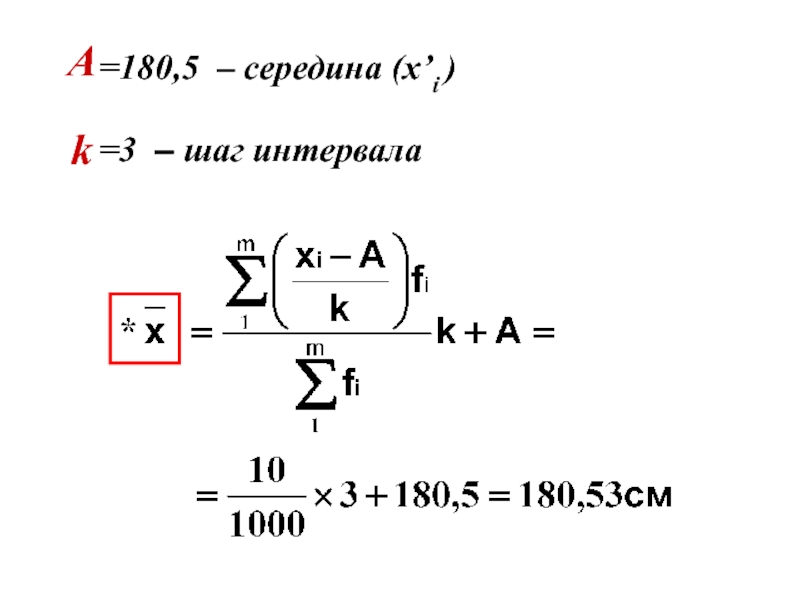
- 34. =180,5 – середина (x’i ) A k =3 – шаг интервала
- 35. Отклонение от ср-й
- 36. q – доля единиц в совокупности, не
- 37. Измерение дисперсии альтернативного признака Дисперсия альтернативного
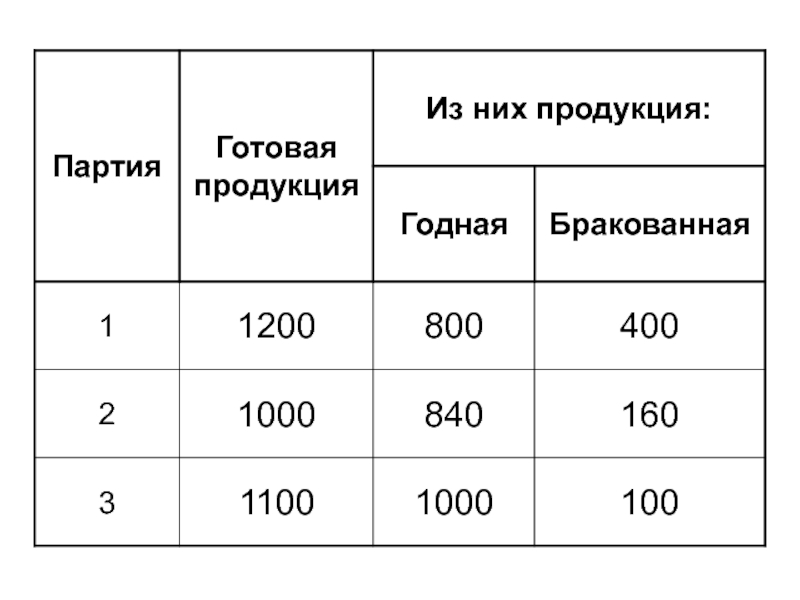
- 39. *Средний % годной продукции *Средний % браковой
- 40. *Среднее квадратическое отклонение удельного веса годной продукции
- 41. Виды дисперсий 1) Общая дисперсия
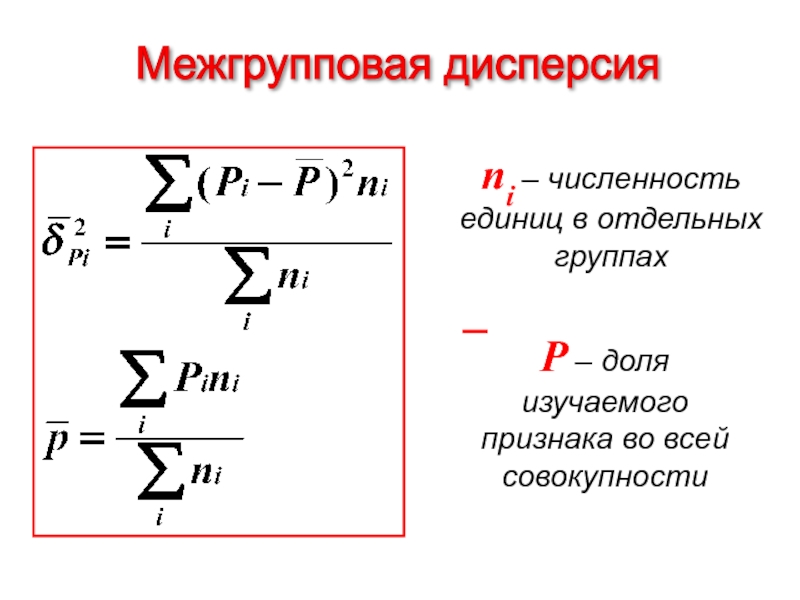
- 42. 2) Межгрупповая дисперсия Виды дисперсий
- 43. 3) Внутригрупповая дисперсия Виды дисперсий
- 44. 3*) Средняя из внутригруппных дисперсий Виды дисперсий
- 45. Правило сложения дисперсий
- 46. Эмпирический коэфициент детерминации
- 47. Эмпирическое корреляционное отношение Изменяется от 0 до 1
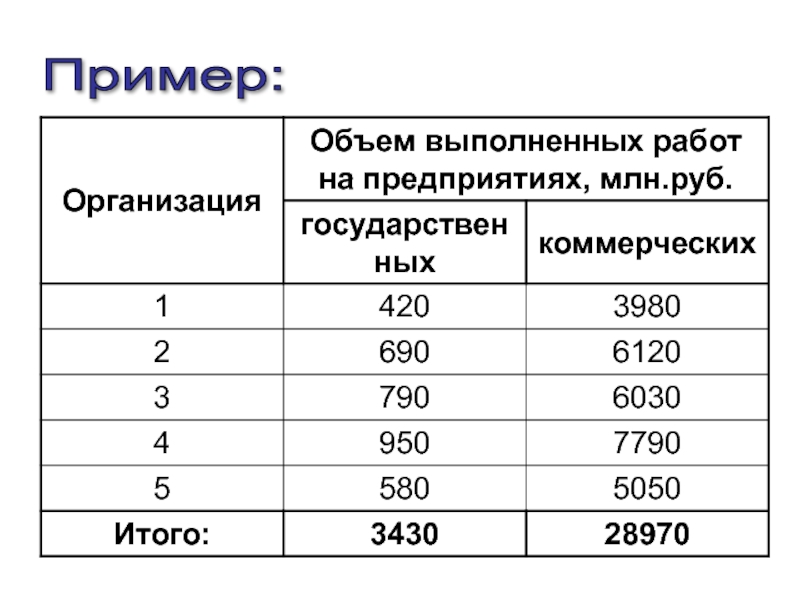
- 48. Пример:
- 49. Алгоритм решения 1) Определим общую среднюю:
- 50. Алгоритм решения 2) Определим среднюю по каждой группе:
- 51. Алгоритм решения 3) Рассчитаем внутригрупповые дисперсии:
- 52. Алгоритм решения 3) Рассчитаем внутригрупповые дисперсии:
- 53. Алгоритм решения 4) Рассчитаем общую дисперсию:
- 54. Алгоритм решения 5) Рассчитаем среднюю из внутригрупповых дисперсий:
- 55. Алгоритм решения 6) Рассчитаем межгрупповую дисперсию:
- 56. Алгоритм решения 7) Найдем общую дисперсию по приему сложения дисперсий
- 57. Алгоритм решения 8) Рассчитаем коэффициент детерминации 9) Определим эмпирическое корреляционное отношение
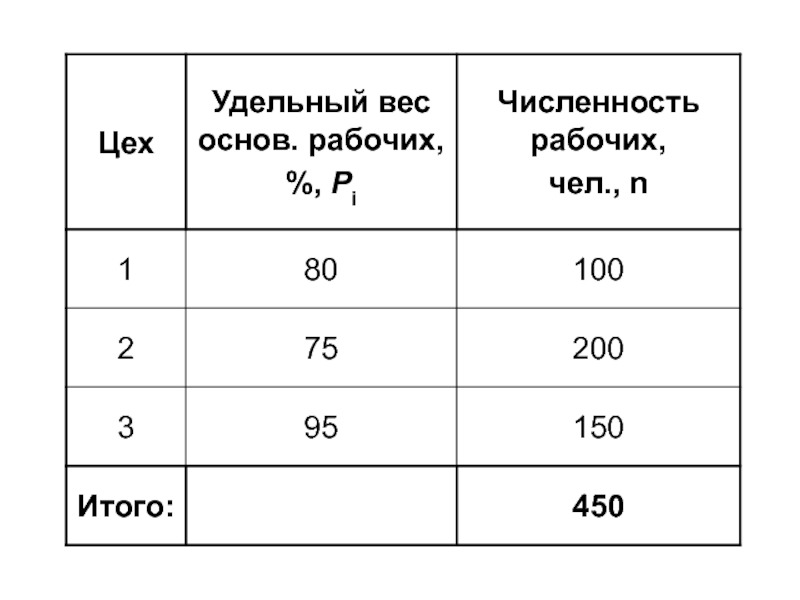
- 58. Внутригрупповая дисперсия доли Pi – доля изучаемого признака в отдельных группах
- 59. Средняя из внутригрупповых дисперсий
- 60. Межгрупповая дисперсия ni – численность единиц в отдельных группах
- 61. Общая дисперсия
- 63. 1) Определяем долю изучаемого признака в совокупности в целом 2) Определяем общую дисперсию доли
- 64. 3) Определяем внутригрупповые дисперсии 4) Вычисляем среднюю из внутригрупповых дисперсий
- 65. 5) Определяем межгрупповую дисперсию
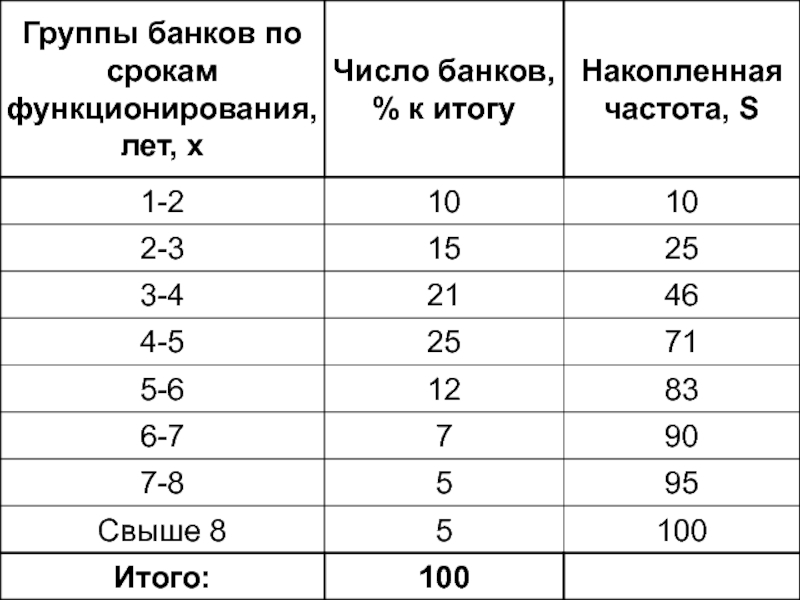
- 66. Расчет по интервальному вариационному ряду
- 67. xQ1 – нижняя граница интервала, содержащего нижний
- 68. SQ1-1 – накопленная частота интервала, предшествующего интервалу,
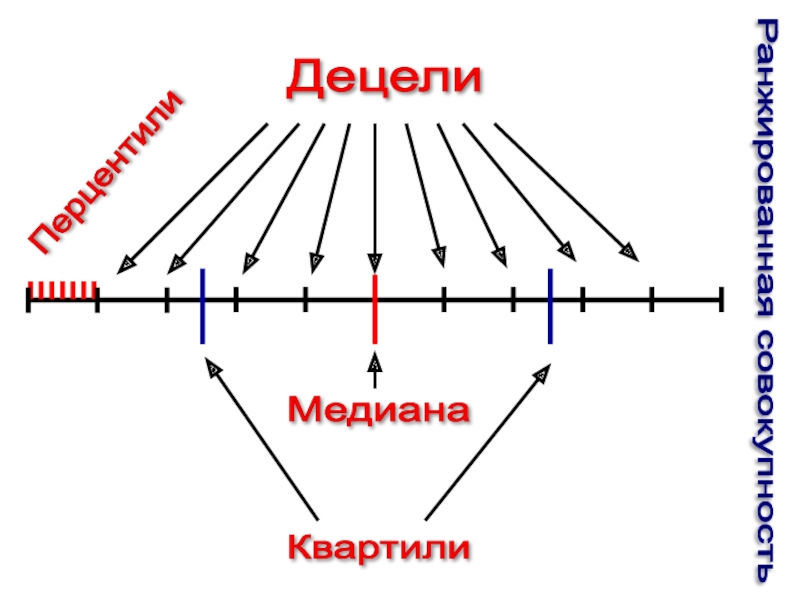
- 71. Децили
- 72. Пример:
- 73. Перцентильный ранг
- 74. Pn – обозначение n-ого перцентиля L –
- 75. Пример: 34% оценок в распределении
- 76. Децели Перцентили Медиана Квартили Ранжированная совокупность
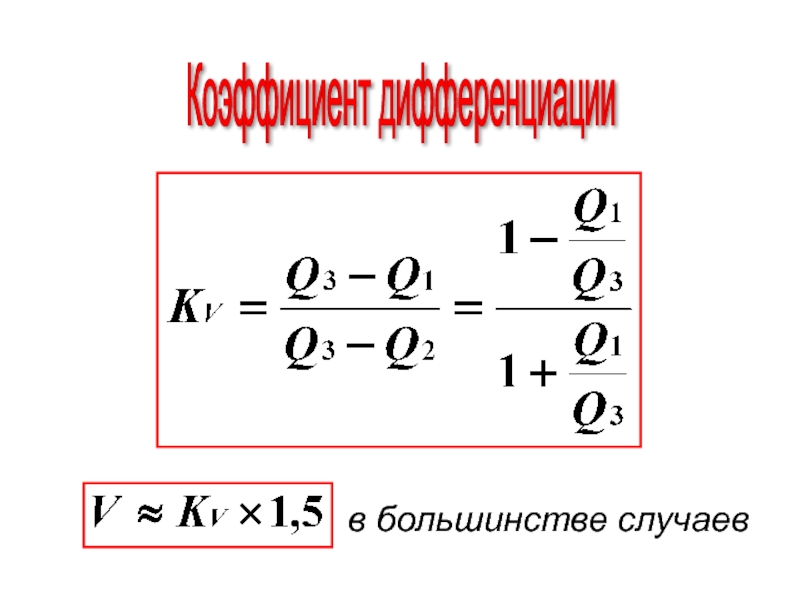
- 77. Коэффициент дифференциации в большинстве случаев
- 78. Децильный коэффициент дифференциации Не совсем точен: сопоставляется min и max величины
- 79. Коэффициент фондовой дифференциации
- 80. – сумма значений признака 10% самых крупных
- 81. Пример: Капитал, млн.руб.: 6,9 9,3 1,3
- 82. 10% самых крупных и 10% самых мелких банков Уровень дифференциации достаточно высок
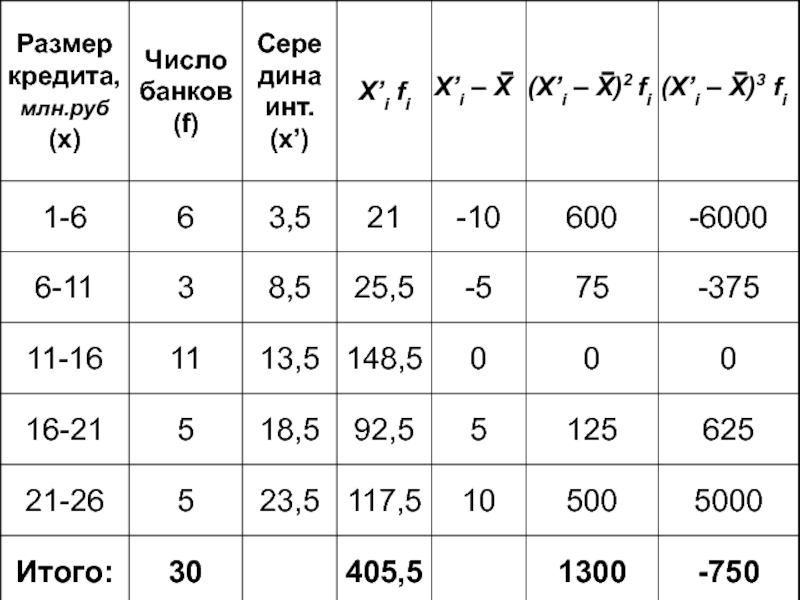
- 83. Моменты распределения Момент k-ого порядка Эмпирический мoмент k-ого порядка
- 84. 1) Начальные моменты
- 85. 2) Условные моменты (Производная величина)
- 86. 3) Центральные моменты (Средняя арифметическая)
- 87. По- рядок Виды
- 88. Относительный показатель ассиметрии ИЛИ
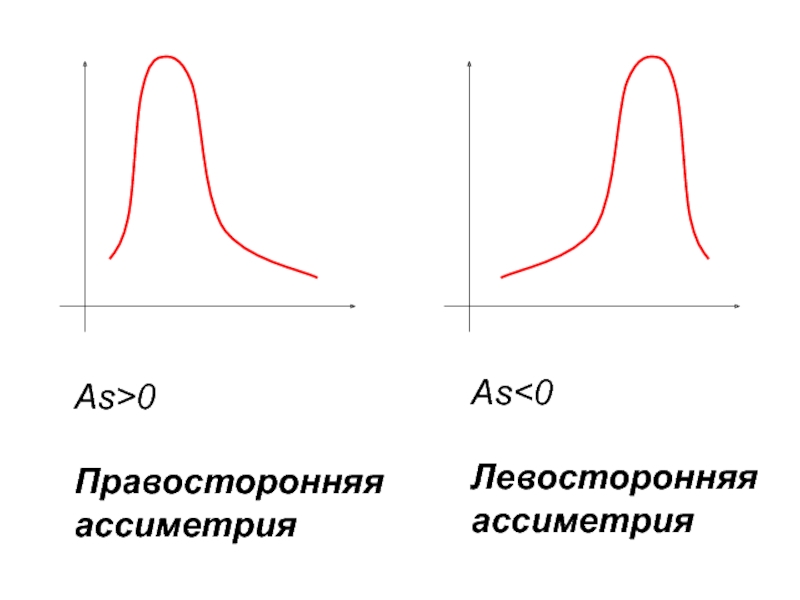
- 89. As>0 Правосторонняя ассиметрия As
- 90. Коэффициент ассиметрии Ассиметрия выше 0,5 считается значительной, меньше 0,25 - незначительной
- 91. Средняя квадратическая ошибка коэффициента ассиметрии
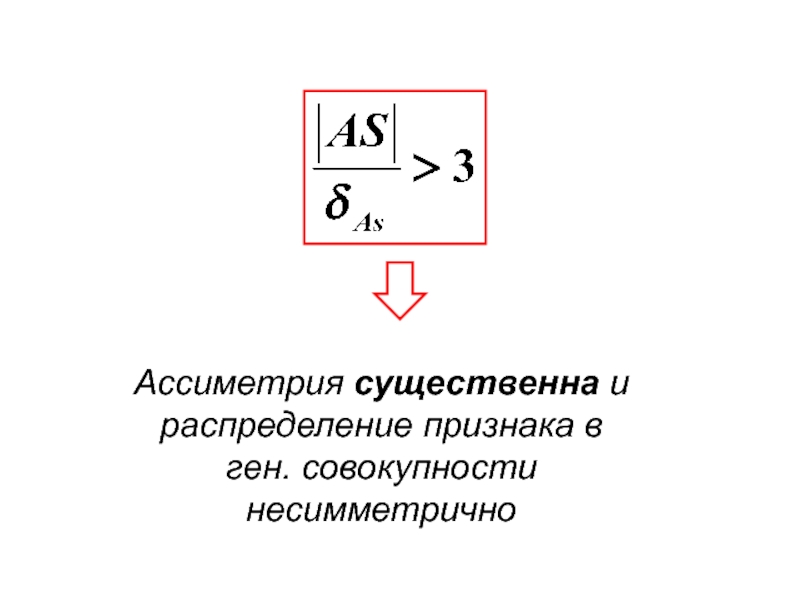
- 92. Ассиметрия существенна и распределение признака в ген. совокупности несимметрично
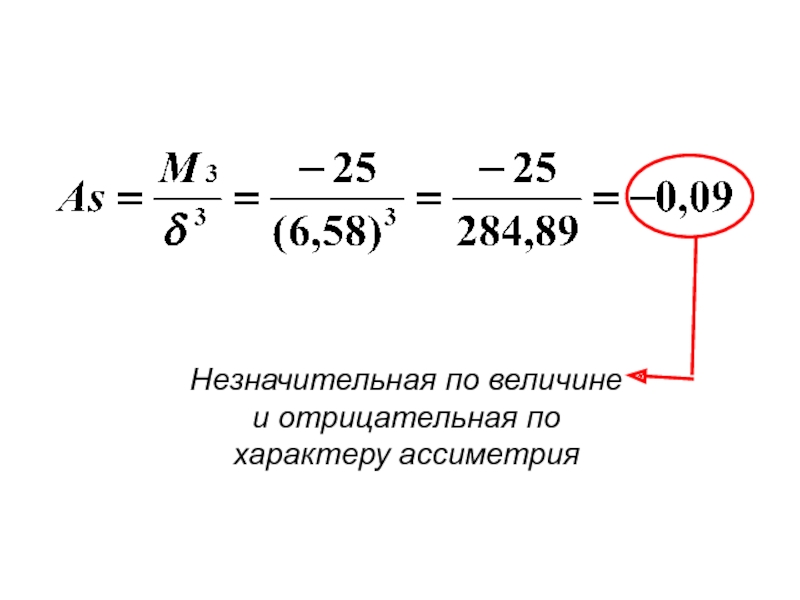
- 95. Незначительная по величине и отрицательная по характеру ассиметрия
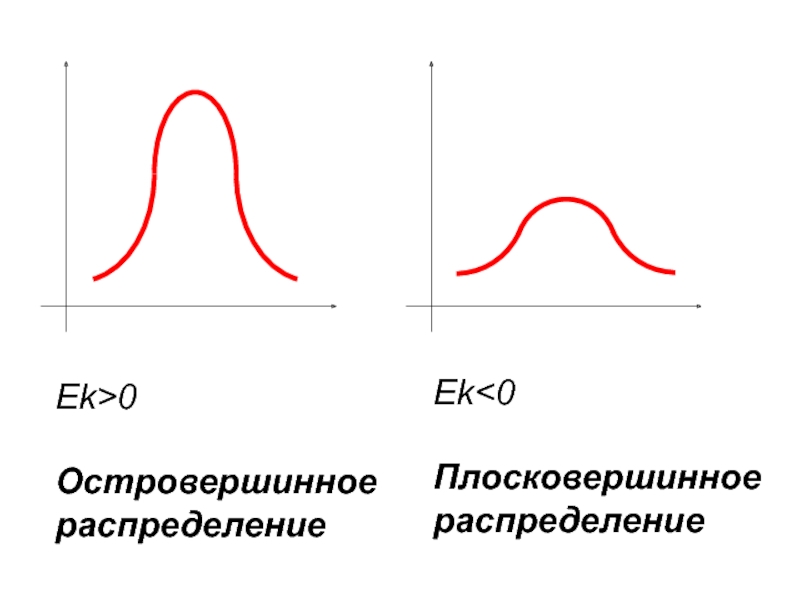
- 96. Показатель эксцесса В нормальном распределении Ek=0
- 97. Ek>0 Островершинное распределение Ek
- 98. Средняя квадратическая ошибка эксцесса Где n – число наблюдений
- 99. Нормальное распределение
- 100. – ордината кривой нормального распределения – стандартизированное
- 102. нормированное
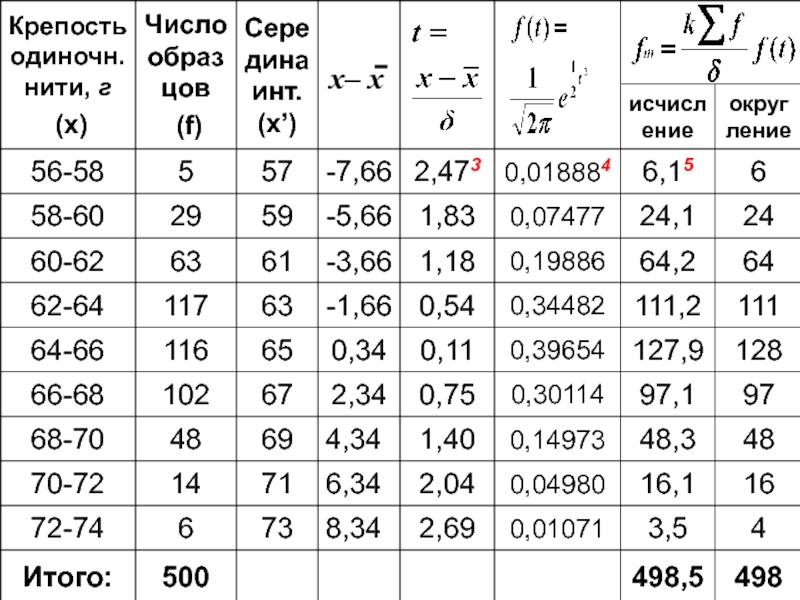
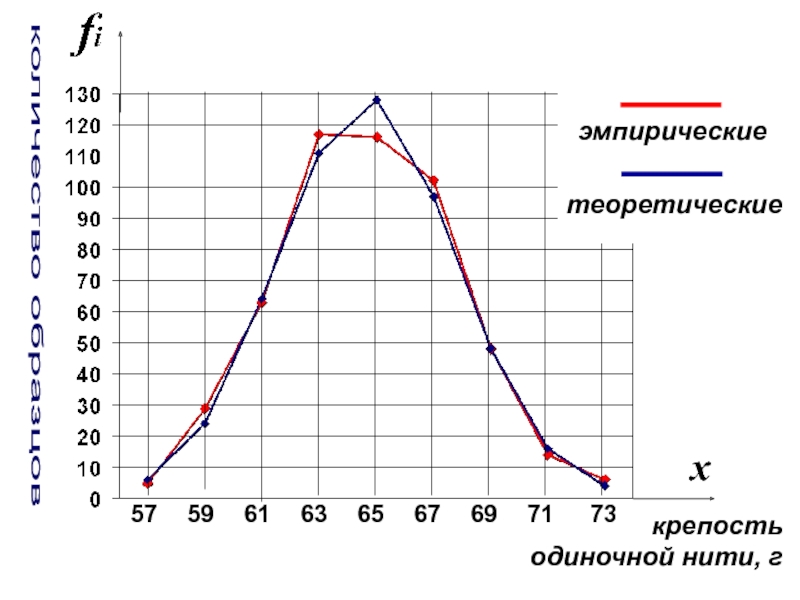
- 103. 57 59 61 63 65 67 крепость
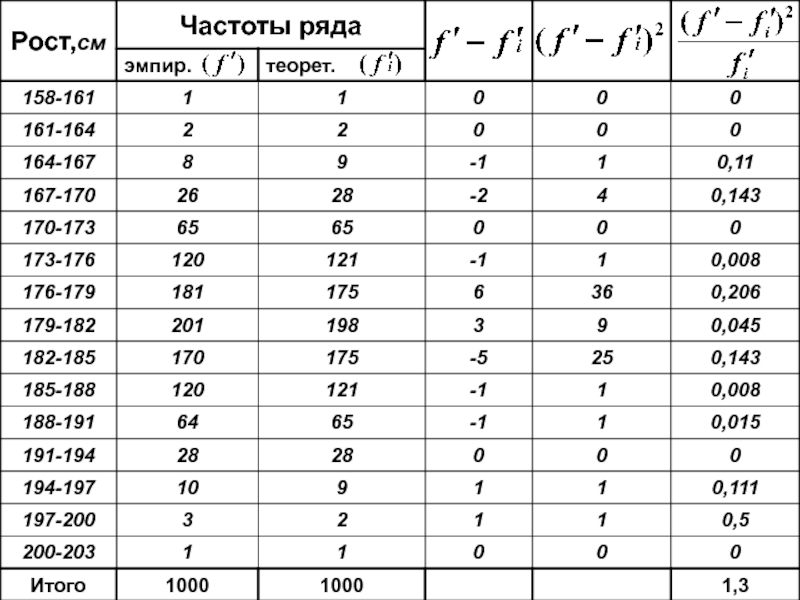
- 104. Критерий согласия 1) Пирсона: –
- 105. Вероятность
- 106. Критерий согласия 2) Романовского: C
- 107. Критерий согласия 3) Колмогорова: Большое число наблюдений (не
- 109. (Критерий согласия Пирсона) (Критерий согласия Романовского)
- 111. max разрыв = 5 (Критерий согласия Колмогорова)
– соответственно нижняя граница и величина модального интервала – частоты (частости) модального, предмодального и послемодального интервалов x0 и i FMo FMo-1 FMo+1 Где:
Слайд 3– соответственно нижняя граница и величина модального интервала
– частоты (частости) модального,
предмодального и послемодального интервалов
x0 и i
FMo
FMo-1
FMo+1
Где:
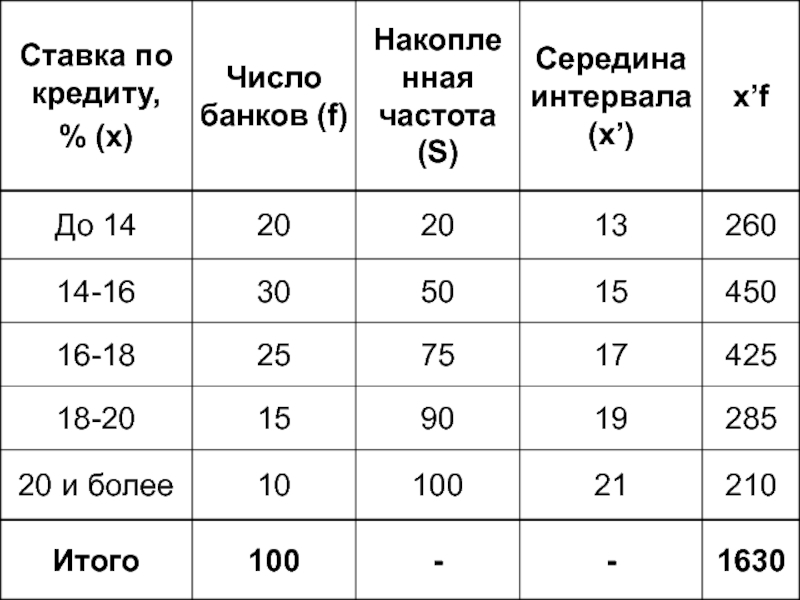
Слайд 5 Ширина интервала i=2
Нижняя граница x0=14
Частота fMo=30
Предмодальная частота fMo-1=20
Послемодальная частота fMo+1=25
Частота fMo=30
Предмодальная частота fMo-1=20
Послемодальная частота fMo+1=25
14-16% - модальный интервал
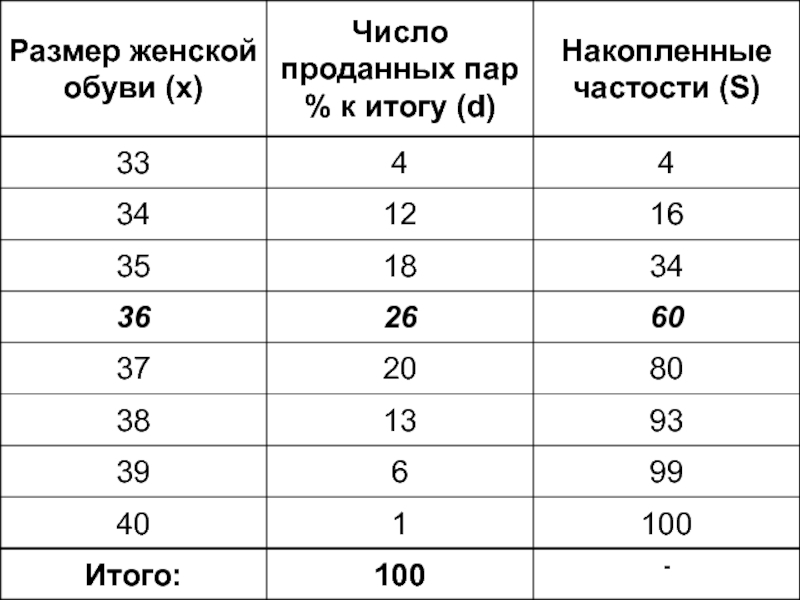
Слайд 75, 4, 3, 4, 5, 5, 6, 2, 6, 3, 5
2,
3, 3, 4, 4, 5, 5, 5, 5, 6, 6
Пример:
1) 11 рабочих, имеющих тарифный разряд:
Ранжирование по разряду:
5ый разряд - центральный и медианный
Слайд 82, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6,
6
Пример:
2) Если ранжированный ряд включает 12 рабочих:
разряда
Слайд 11– соответственно нижняя граница и величина медианного интервала
x0 и i
SMe-1
fMe
– частота
медианного интервала
– накопленная частота предмедианного интервала
Слайд 20Алгоритм расчета
Рассчитаем среднюю величину по формуле средней арифметической взвешенной
2) Определим
произведения значений середины интервалов (x’i ) на соответствующие им веса
Слайд 21Алгоритм расчета
3) Найдем абсолютные отклонения середины интервалов, принятых в качестве
вариантов признака (xi) от средней величины (х)
Слайд 22Алгоритм расчета
Сумму произведений делим на сумму весов
Отклонение от средней в
целом небольшое
Слайд 23Алгоритм расчета
Совокупность в отношении признака однородна, средняя - типична
Отличие от
средней
Слайд 27Алгоритм расчета
1) Определим среднюю величину по исходным данным по формуле
средней арифметической простой (невзвешенной)
Слайд 28Алгоритм расчета
2) Найдем отклонения
3) Возведем отклонения во 2ую степень
4) Разделив
сумму отклонений на число единиц совокупности, получим дисперсию:
Слайд 29Алгоритм расчета
5) Извлечем из дисперсии корень 2ой степени, получим среднее
квадратическое отклонение
Степень вариации невелика, совокупность однородна
Слайд 30Относительные показатели вариации
- коэффициент осцилляции
- линейный коэффициент вариации
или
Слайд 31Относительные показатели вариации
- коэффициент вариации (относит-й)
Совокупность считается однородной, если
коэффициент вариации не превышает 33 %
Слайд 36q – доля единиц в совокупности, не обладающих данным признаком
p –
доля единиц в совокупности, обладающих данным признаком
Измерение дисперсии альтернативного признака
Среднее значение альтернативного признака
Слайд 37Измерение дисперсии альтернативного признака
Дисперсия альтернативного признака
Предельное значение
при
Слайд 39*Средний % годной продукции
*Средний % браковой продукции
или 80%
или 20%
*Дисперсия удельного веса
годной продукции
Слайд 40*Среднее квадратическое отклонение удельного веса годной продукции
*Коэффициент вариации удельного веса годной
продукции в общем выпуске продукции
Слайд 422) Межгрупповая дисперсия
Виды дисперсий
k – число групп
nj – число
единиц в j-ой группе
xj – частная средняя по j-ой группе
xo – общая средняя по совокупности единиц
xj – частная средняя по j-ой группе
xo – общая средняя по совокупности единиц
Слайд 57Алгоритм решения
8) Рассчитаем коэффициент детерминации
9) Определим эмпирическое корреляционное отношение
Слайд 631) Определяем долю изучаемого признака в совокупности в целом
2) Определяем общую
дисперсию доли
Слайд 67xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по
накопленной частоте, 1ой превышающей 25%)
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, 1ой превышающей 75%)
i – величина интервала
Слайд 68SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль
SQ3-1 –
накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль
fQ3 – частота интервала, содержащего верхний квартиль
fQ1 – частота интервала, содержащего нижний квартиль
Слайд 74Pn – обозначение n-ого перцентиля
L – нижняя граница интервала
S – число
оценок, необходимое, чтобы попасть в точку на горизонтальной оси, которая соответствует данному перцентилю
i – расстояние от нижней границы L до верхней границы L+1 (шаг интервала)
f – число оценок, расположенных в интервале от L до L+1
Слайд 75Пример:
34% оценок в распределении ниже оценки студента Иванова
2%
от всех оценок распределения составляет оценка студента Иванова
Перцентильный ранг оценки студента Иванова
Слайд 80– сумма значений признака 10% самых крупных единиц в совокупности
– число
единиц совокупности самых крупных и мелких
– сумма значений признака 10% самых мелких единиц в совокупности
n
Слайд 90Коэффициент ассиметрии
Ассиметрия выше 0,5 считается значительной, меньше 0,25 - незначительной
Слайд 100– ордината кривой нормального распределения
– стандартизированное отклонение
– материальные постоянные
(= 2,7182 и
3,1415 соответственно)
– варианты вариационного ряда
– их средняя величина
– среднее квадратическое отклонение
и
Слайд 102
нормированное отклонение (t)
по приложению значения плотности вероятности для нормированного
нормального закона распределения
Слайд 105Вероятность определения по приложению:
–
эмпирические и теоретические распределения близки
– совпадение удовлетворительное
– совпадение недостаточное
В остальных случаях
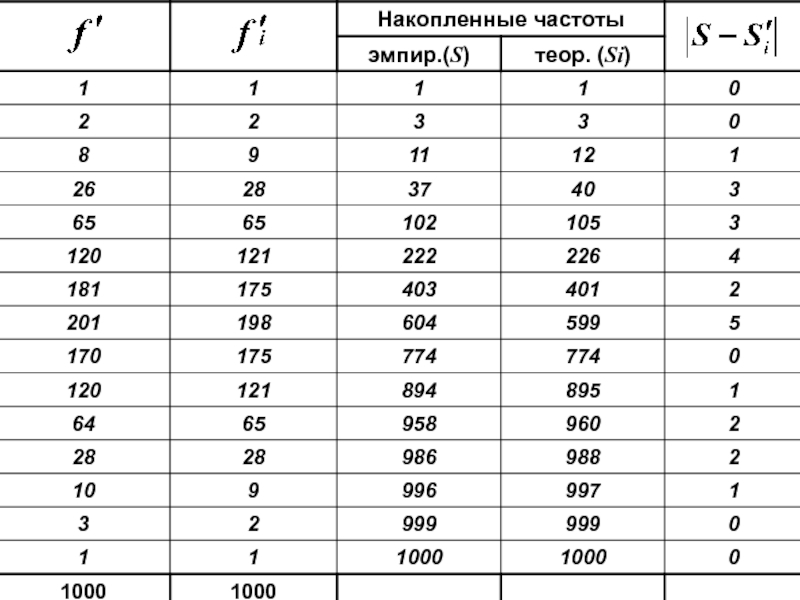
Слайд 107Критерий согласия
3) Колмогорова:
Большое число наблюдений (не
между накопленными эмпирическими и теоретическими частотами
D
– сумма эмпирических частот
Ef
Слайд 111max разрыв = 5
(Критерий согласия Колмогорова)
Распределение нормальное, отклонения эмпирических частот от
теоретических случайные
