Функции, их свойства и графики
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции, их свойства и графики презентация
Содержание
- 1. Функции, их свойства и графики
- 2. Цели урока: Ознакомиться с понятием
- 3. Немного истории Слово "функция" (от латинского functio
- 4. Определение. «Зависимость переменной y от переменной x,
- 5. Общая схема исследования функции
- 6. Область определения функции Областью определения (существования) функции
- 7. [-3;5] 0 х у 7
- 8. Множество значений функции. Множеством значений
- 9. Найдите множество значений функции,
- 10. Исследование функции на четность. Функция
- 11. На одном из следующих рисунков изображен
- 12. Функция
- 13. 1
- 14. Среди множества функций есть функции, значения которых
- 15. 1 2 3 4 [-6;7] [-5;-3] U
- 16. y х 1 2 3 4 1
- 17. Какие из функций являются возрастающими, а какие убывающими?
- 18. Исследование функции на монотонность. Как
- 19. Исследовать функцию на монотонность Функция у=х2
- 20. Обратная функция Если функция
- 21. Диктант Найти область значений
- 22. Функции. 1. Линейная функция
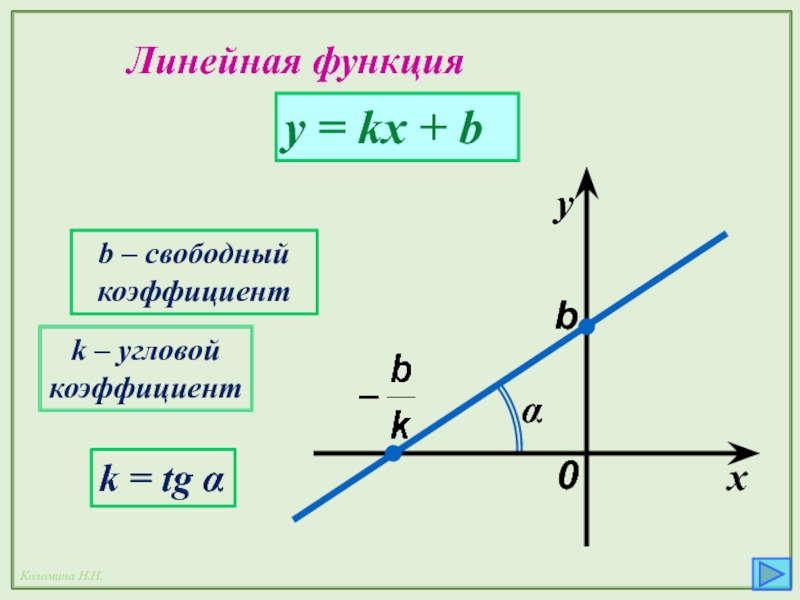
- 23. Линейная функция y = kx + b
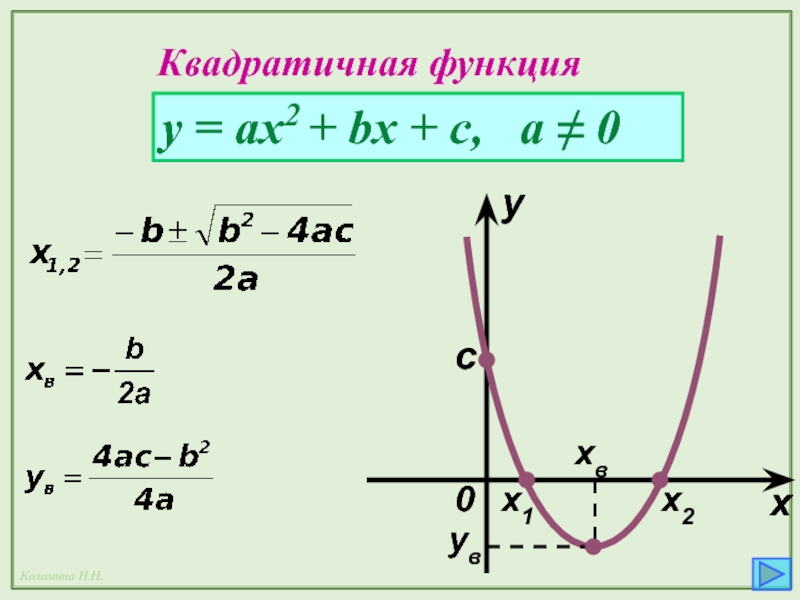
- 24. Квадратичная функция y = ax2 + bx
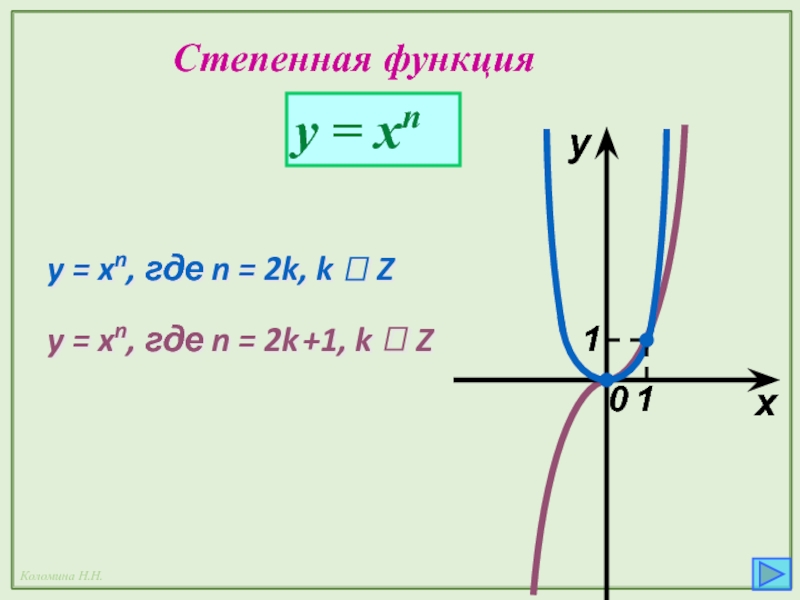
- 25. Степенная функция y = xn x y
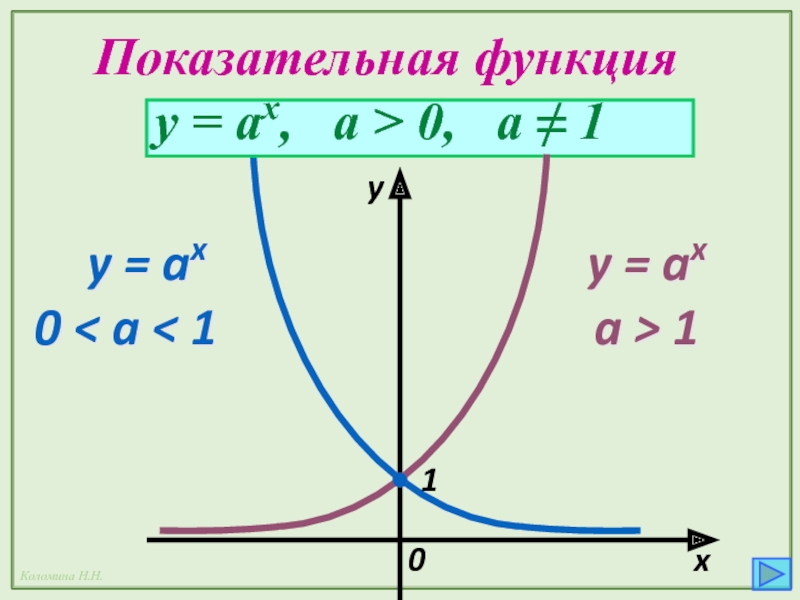
- 26. Показательная функция x y y = ax,
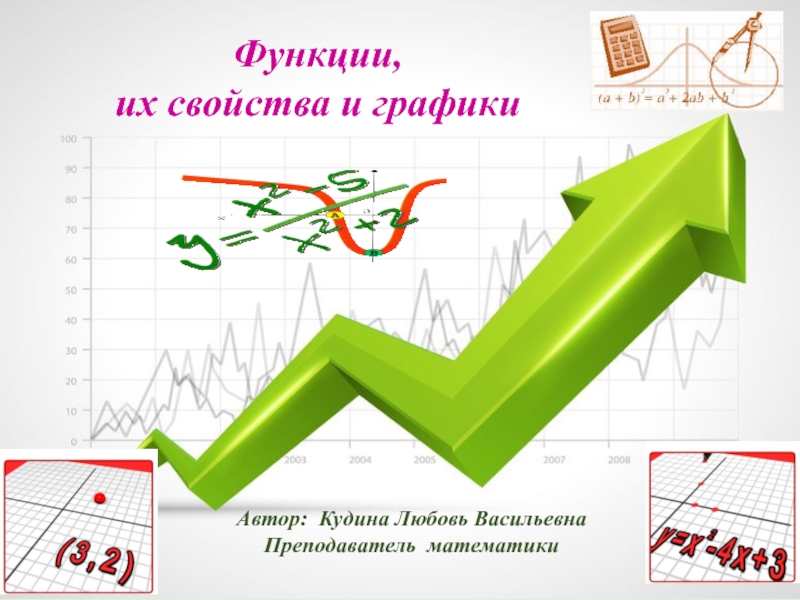
- 27. Логарифмическая функция y = loga x a
- 28. Самостоятельная работа
- 29. Вопросы для повторения 1.Сформулируйте определение
Слайд 2Цели урока:
Ознакомиться с понятием «функция», закрепить его на
Усвоить новые термины
Узнать методы исследования функции
Закрепить знания по теме при решении задач
Научиться строить графики функций
Слайд 3Немного истории
Слово "функция" (от латинского functio — совершение, выполнение) впервые употребил
В главном математическом труде "Геометрия" (1637) Рене Декарта
впервые введено понятие переменной величины, создан метод координат, введены значки для переменных величин (x, y, z, ...)
Определения функции «Функция переменного количества есть аналитическое выражение,
cоставленное каким-либо образом из этого количества и чисел или постоянных количеств» сделал в 1748 г. немецкий и российский математик Леонард Эйлер
Слайд 4Определение.
«Зависимость переменной y от переменной x, при которой каждому значению переменной
Символически функциональная зависимость между переменной у (функцией) и переменной х (аргументом) записывается с помощью равенства
Способы задания функций: табличный (таблица), графический(график), аналитический (формула).
Слайд 5Общая схема исследования функции
Слайд 6Область определения функции
Областью определения (существования) функции называется множество всех действительных значений
Например, для функции у=х областью определения является множество всех действительных значений чисел R ; для функции у=1/х областью определения является множество R кроме х=0.
Слайд 7[-3;5]
0
х
у
7
-5
1
Подумай!
2
[-5;7)
3
[-5;7]
Подумай!
4
(-3;5]
Подумай!
Проверка (1)
Найдите область определения функции, график которой изображен на
5
-3
Верно!
Область определения функции – значения, которые принимает независимая переменная х.
Слайд 8Множество значений функции.
Множеством значений функции называется множество всех действительных
Например, множеством значений функции у= х+1 является множество R,
множеством значений функции является множество действительных чисел, больше или равных 1.
у= Х2 +1
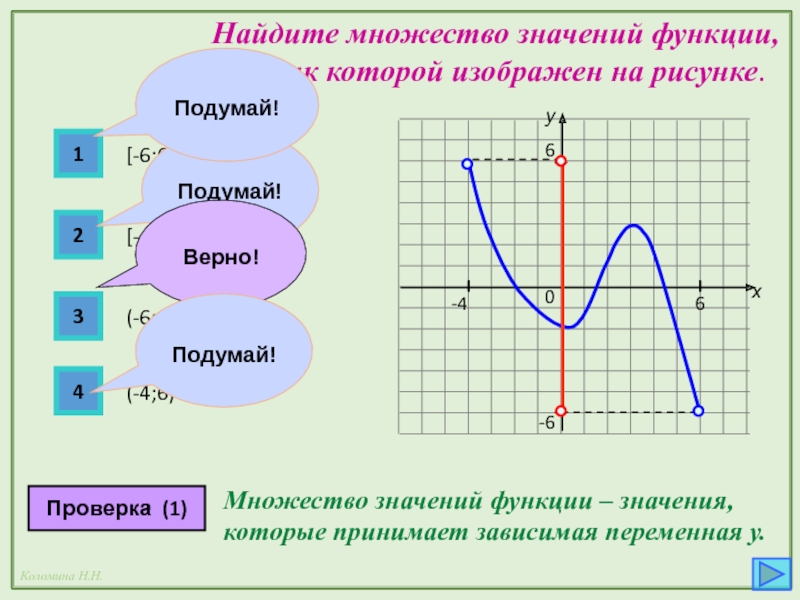
Слайд 9 Найдите множество значений функции,
у
х
0
-6
-4
6
6
1
2
3
4
Проверка (1)
(-4;6)
[-6;6]
(-6;6)
[-4;6]
Подумай!
Верно!
Подумай!
Подумай!
Множество значений функции – значения, которые принимает зависимая переменная у.
Слайд 10Исследование функции на четность.
Функция
Например, парабола у= Х2 является четной функцией, т.к. (-Х2)= Х2 .
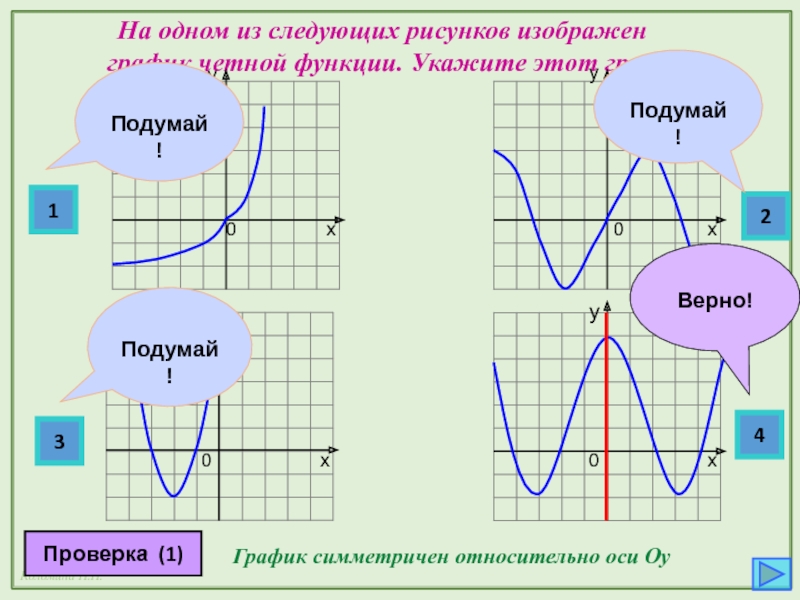
График четной функции симметричен относительно оси оу.
Слайд 11 На одном из следующих рисунков изображен
х
х
х
х
у
у
у
у
1
3
2
4
Подумай!
Верно!
Проверка (1)
График симметричен относительно оси Oу
Подумай!
0
0
0
0
Подумай!
Слайд 12Функция называется
Например, функция у= Х3 – нечетная, т.к. (-Х)3 = -Х3.
График нечетной функции симметричен относительно начала координат.
Свойством четности или нечетности обладает не всякая функция. Например, функция
не является ни четной, ни нечетной:
Х2+ Х3
(-Х)2+ (-Х)3 = Х2 – Х3;
Х2 + Х3
Х2 – Х3;
=
/
Слайд 13
1
2
3
4
х
х
х
х
у
у
у
у
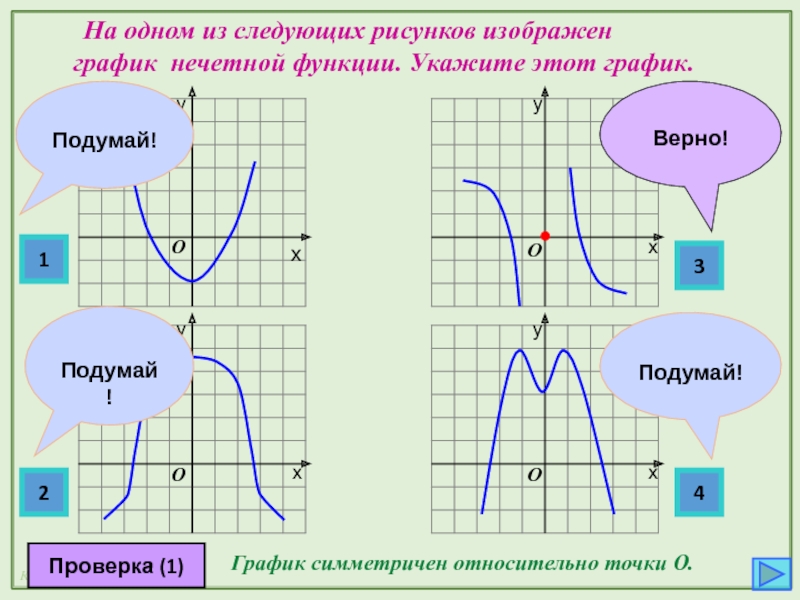
На одном из следующих рисунков изображен
Подумай!
Верно!
Подумай!
Проверка (1)
График симметричен относительно точки О.
Подумай!
О
О
О
О
Слайд 14Среди множества функций есть функции, значения которых с увеличением аргумента только
Функция называется возрастающей в промежутке а х в, если для любых Х1 и , принадлежащих этому промежутку, при Х1 Х2 имеет место неравенство
Определение промежутков возрастания и убывания
/\
/\
Х2
/\
/\
1
2
Функция называется убывающей в промежутке а х в, если для любых Х1 и Х2, принадлежащих этому промежутку, при Х1 Х2 имеет место неравенство
/\
/\
/\
2
1
>
Слайд 151
2
3
4
[-6;7]
[-5;-3] U [2;6]
[-3;7]
[-3;2]
Проверка (1)
х
0
2
6
-5
7
-3
-6
Подумай!
Подумай!
-2
3
Подумай !
На рисунке изображен график функции y
у
Верно!
Слайд 16y
х
1
2
3
4
1
2
4
0
Подумай!
Подумай!
Верно!
Подумай!
Проверка (1)
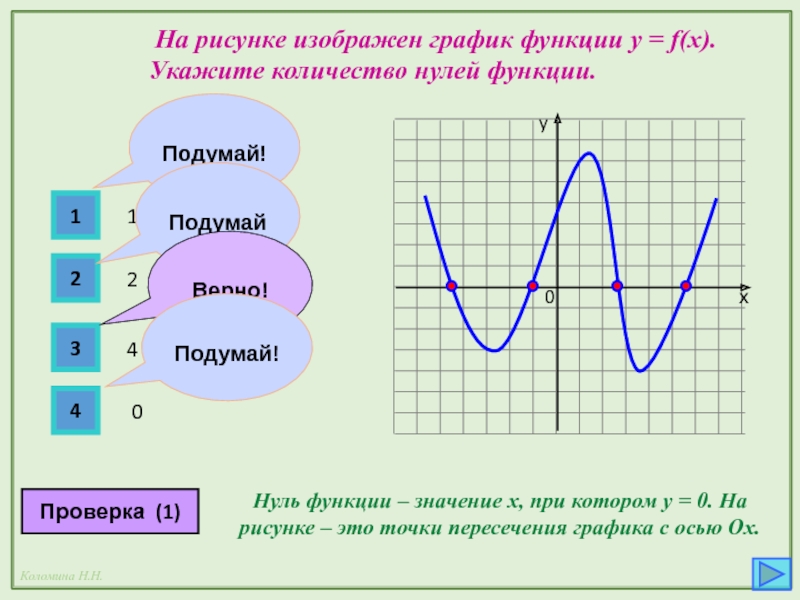
Нуль функции – значение х, при котором y = 0.
На рисунке изображен график функции y = f(x). Укажите количество нулей функции.
0
Слайд 18Исследование функции на монотонность.
Как возрастающие, так и убывающие функции
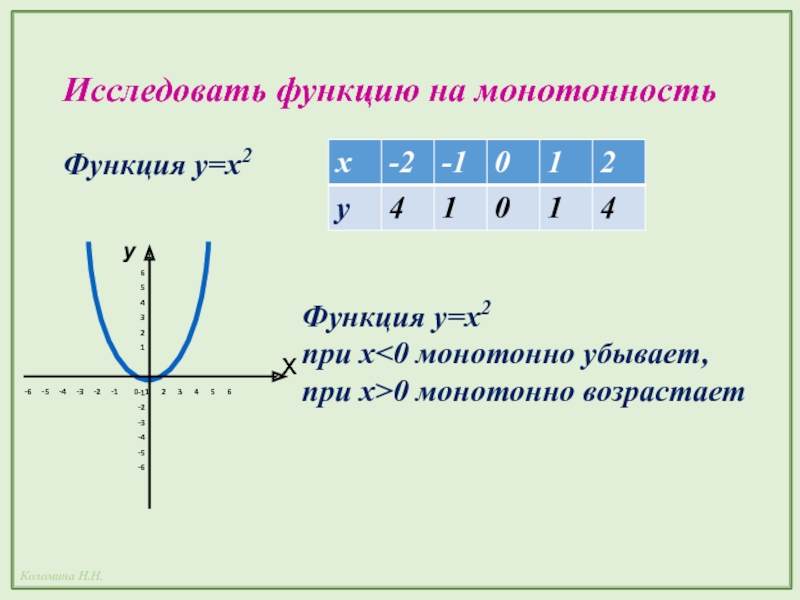
Например, функция у= Х2 при х 0 монотонно возрастает.
Функция у= Х3 на всей числовой оси монотонно возрастает, а
функция у= -Х3 на всей числовой оси монотонно убывает.
/\
/\
Слайд 19Исследовать функцию на монотонность
Функция у=х2
Функция у=х2
Слайд 20Обратная функция
Если функция
Например, функция у=3х+5 является обратимой, т.к. каждое значение у принимается при единственном значении аргумента х. Напротив, функция у= 3Х2 не является обратимой, поскольку, например, значение у=3 она принимает и при х=1, и при х=-1.
Для всякой непрерывной функции (такой, которая не имеет точек разрыва) существует монотонная однозначная и непрерывная обратная функция.
Слайд 22Функции.
1. Линейная функция
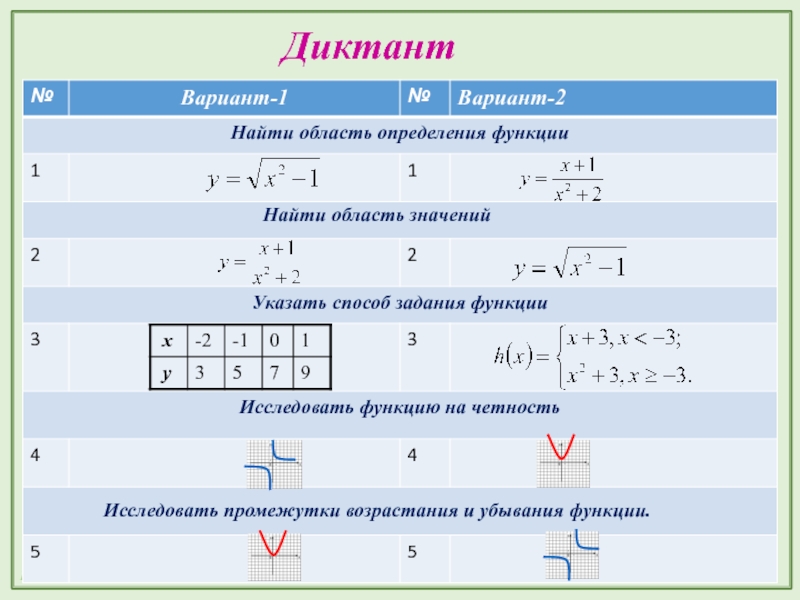
Слайд 28Самостоятельная работа
Вариант-1
Вариант-2
1.
1.
2.
2.
3.
3.
4.
4.
5.
5.
Слайд 29Вопросы для повторения
1.Сформулируйте определение функции.





![[-3;5]0ху7-51Подумай!2[-5;7)3[-5;7]Подумай!4(-3;5]Подумай!Проверка (1) Найдите область определения функции, график которой изображен на рисунке.5-3Верно!Область определения функции – значения,](/img/tmb/4/352915/8364d28975e7cd3116d2ed291017a4f9-800x.jpg)




![1234[-6;7][-5;-3] U [2;6][-3;7][-3;2]Проверка (1)х026-57-3-6Подумай!Подумай!-23Подумай ! На рисунке изображен график функции y = f(x), заданной на](/img/tmb/4/352915/cb4512424aea48240dd798f8366f6339-800x.jpg)