- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка к ЕГЭ. Решение задач С2 презентация
Содержание
- 1. Подготовка к ЕГЭ. Решение задач С2
- 2. Типы задач С2 Расстояние между двумя точками
- 3. Расстояние между двумя точками Пусть
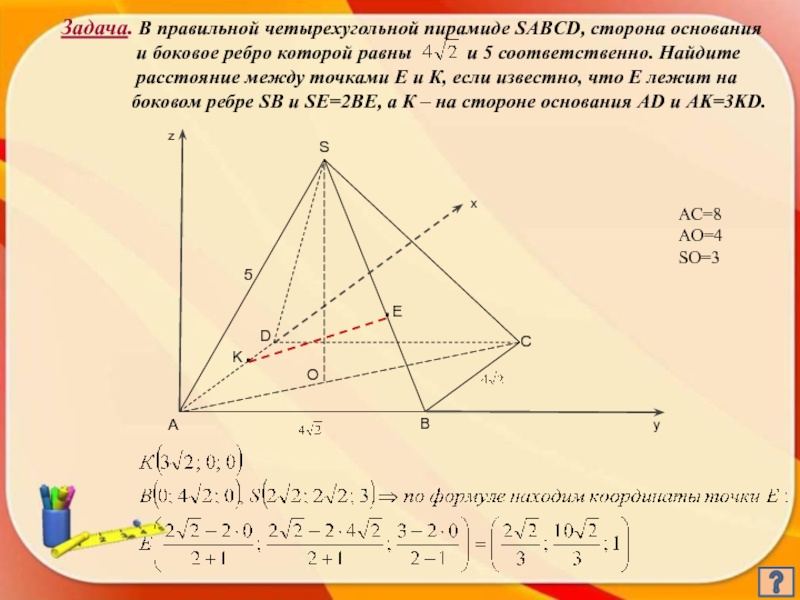
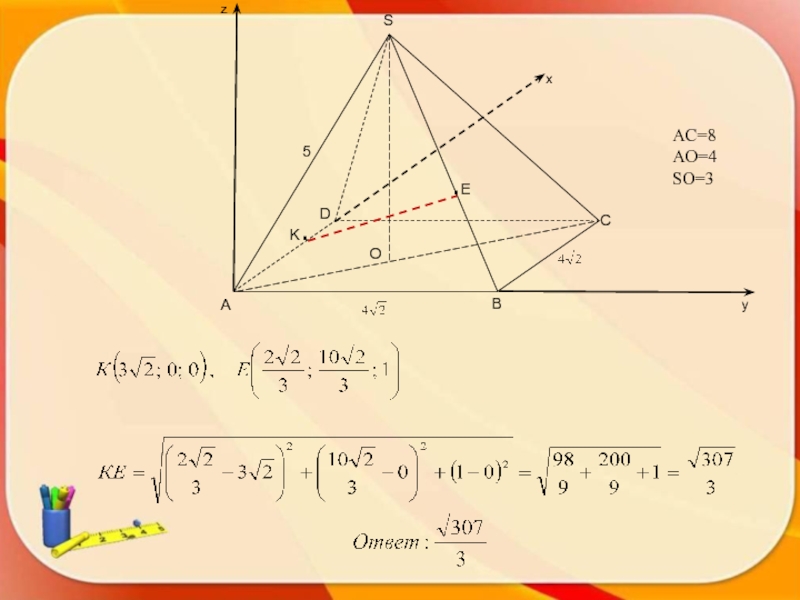
- 4. Задача. В правильной четырехугольной пирамиде SABCD, сторона
- 5. AC=8 AO=4 SO=3
- 6. Расстояние от точки до плоскости Координатный метод
- 7. Задача (ЕГЭ, 2012). В правильной треугольной
- 8. Угол между прямой и плоскостью Векторно -
- 9. Задача. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
- 10. Угол между плоскостями Векторно - координатный метод
- 11. Задача (ЕГЭ, 2012). В правильной четырёхугольной
- 12. Спасибо за внимание!
- 13. Пусть точки
- 14. Расстояние от точки до плоскости Координатный метод
- 15. Угол между прямой и плоскостью Векторно -
- 16. Угол между плоскостями Векторно - координатный метод
Слайд 1Подготовка к ЕГЭ.
Решение задач С2.
Коткова Евгения Сергеевна,
учитель математики
МБОУ «Лицей
I квалификационная категория
Слайд 2Типы задач С2
Расстояние между двумя точками
Расстояние от точки до плоскости
Угол между
Угол между плоскостями
Слайд 3Расстояние между двумя точками
Пусть точки
Слайд 4Задача. В правильной четырехугольной пирамиде SABCD, сторона основания
расстояние между точками Е и К, если известно, что Е лежит на
боковом ребре SB и SE=2BE, а К – на стороне основания AD и AK=3KD.
А
В
С
D
S
K.
.E
z
y
x
5
AC=8
AO=4
SO=3
O
Слайд 6Расстояние от точки до плоскости
Координатный метод
Расстояние от точки
Слайд 7
Задача (ЕГЭ, 2012). В правильной треугольной призме ABCA1B1C1 стороны
середина ребра CC1. Найдите расстояние от вершины
С до плоскости ADB1.
А
А1
В
В1
С
С1
z
y
x
. D
2
3
О
Решение:
Подставим координаты точек в уравнение плоскости ax+by+cz+d=0,
Вычислим расстояние от точки С до плоскости ADB1 по формуле:
Слайд 8Угол между прямой и плоскостью
Векторно - координатный метод
Угол между
Слайд 9
Задача. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона
и плоскостью AF1C1.
Решение:
А
А1
В
В1
С
С1
D
E
F
D1
E1
F1
y
x
z
3
1
Слайд 10Угол между плоскостями
Векторно - координатный метод
Задачу о нахождении угла
Слайд 11
Задача (ЕГЭ, 2012). В правильной четырёхугольной призме ABCDA1B1C1D1
На ребре АА1 отмечена точка Е так, что АЕ:ЕА1=3:2.
Найдите угол между плоскостями АВС и BED1.
А
А1
В
В1
С
С1
D
D1
E .
y
x
z
2
5
Решение:
Составим уравнение плоскости BED1.
В(2;0;0), Е(0;0;3), D1(0;2;5)
Подставим координаты точек в уравнение плоскости ax+by+cz+d=0,
Т. к. ось Аz перпендикулярна плоскости основания, то нормальный вектор плоскости АВС имеет координаты
Слайд 13 Пусть точки
Расстояние между двумя точками
Слайд 14Расстояние от точки до плоскости
Координатный метод
Расстояние от точки
Слайд 15Угол между прямой и плоскостью
Векторно - координатный метод
Угол между
Слайд 16Угол между плоскостями
Векторно - координатный метод
Задачу о нахождении угла