- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебраические дроби презентация
Содержание
- 1. Алгебраические дроби
- 2. Алгебраические дроби Дроби:
- 3. Функция 1.функция-зависимость (соответствие) X
- 4. Свойства функции 1.D(f) 2.Е(f) 3.Точки пересечения с осями 4.Промежутки знакопостояства (f(x)>0 ,f(x)
- 5. Алгебраические выражения Числовые (арифметические)
- 6. Многочлены 1.Одночлен -бук. часть,умн.,степ.
- 7. продолжение 3.Разложение на множители
- 8. Формулы
- 9. Уравнение (равенство с переменной) 1.Корень -значение переменной
- 10. Линейное уравнение
- 11. Степень
- 12. Свойства степени 1.
- 13. Системы уравнений Система-это несколько уравнений , для
- 14. Система линейных уравнений а)
- 15. Неравенства a>b ,то a-b>0
- 16. Квадратные уравнения Неприведенное :
- 17. Существование корней 1.D>0 -два действительных корня 2.D=0 –два действительных равных 3.D
- 18. Квадратные корни 1.
- 19. Действительные числа Состав
- 20. Корни натуральной степени 1.
- 21. Арифметическая прогрессия 1.
- 22. Геометрическая прогрессия 1.
- 23. Бесконечно убывающая прогрессия 1.
Слайд 3Функция
1.функция-зависимость (соответствие) X
Х-аргумент, D(f)-область определения
У- значение функции , Е(f)-область значений
2.График-множество всех точек (х;у) ,где у=f(x)
3.Способы задания
1) формула
2)график
3)таблица
4) ОПИСАНИЕ
5) СИСТЕМА УРАВНЕНИЙ
2.График-множество всех точек (х;у) ,где у=f(x)
3.Способы задания
1) формула
2)график
3)таблица
4) ОПИСАНИЕ
5) СИСТЕМА УРАВНЕНИЙ
Слайд 4Свойства функции
1.D(f)
2.Е(f)
3.Точки пересечения с осями
4.Промежутки знакопостояства (f(x)>0 ,f(x)
(f(-x)=f(x)) или нечетность (f(-x)=-f(x))
7.Периодичность (f(x+T)=f(x))
8.Экстремумы (max,min)
9.Поведение вблизи особых точек или
10.График
7.Периодичность (f(x+T)=f(x))
8.Экстремумы (max,min)
9.Поведение вблизи особых точек или
10.График
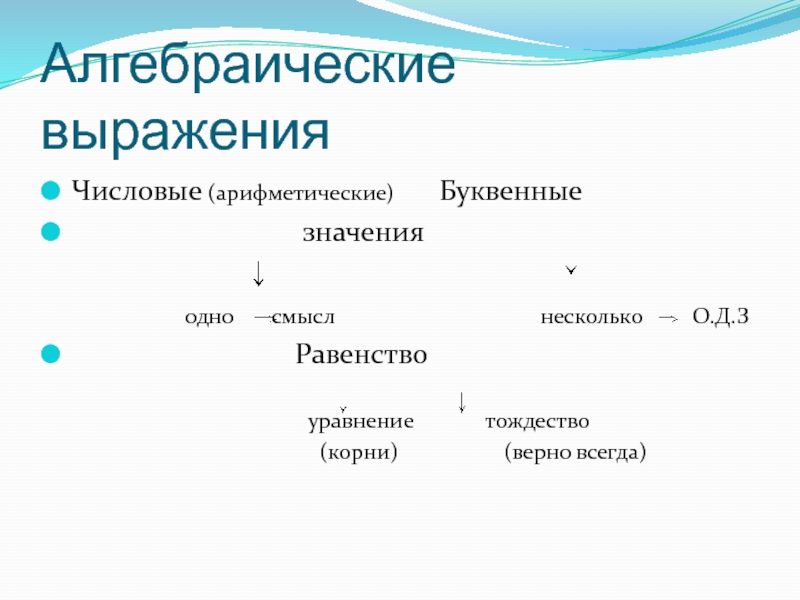
Слайд 5Алгебраические выражения
Числовые (арифметические) Буквенные
значения
одно смысл несколько О.Д.З
Равенство
уравнение тождество
(корни) (верно всегда)
одно смысл несколько О.Д.З
Равенство
уравнение тождество
(корни) (верно всегда)
Слайд 6Многочлены
1.Одночлен -бук. часть,умн.,степ.
стандартный вид: -7
(-7 коэффициент) ,степень:3+1+2,
подобные:бук. части одинак.
2.Многочлен-сумма одночленов (стандарт. вид,степень)
3.Действия
(+) и (-) раскрытие скобок
(х) на одночлен «фонтанчик»
(х) на многочлен «фонтан»
(:) на одночлен «по очереди)
(:) на многочлен
подобные:бук. части одинак.
2.Многочлен-сумма одночленов (стандарт. вид,степень)
3.Действия
(+) и (-) раскрытие скобок
(х) на одночлен «фонтанчик»
(х) на многочлен «фонтан»
(:) на одночлен «по очереди)
(:) на многочлен
Слайд 7продолжение
3.Разложение на множители
а) вынесение общего множителя за скобки
б) группировка
в)применение формул сокращенного умножения
в)применение формул сокращенного умножения
Слайд 9Уравнение (равенство с переменной)
1.Корень -значение переменной ,при котором равенство верно
Уравнения равносильны
одни и те же корни или не имеют их
2.Свойства
= + a = +a
= x a = x a
+ = = - -
2.Свойства
= + a = +a
= x a = x a
+ = = - -
Слайд 10Линейное уравнение
ax =b
Возможные случаи:
1)a 0, x= -единственный корень
2) a=0; b=0 x- число
3)a=0; b 0, - нет корня
Возможные случаи:
1)a 0, x= -единственный корень
2) a=0; b=0 x- число
3)a=0; b 0, - нет корня
Слайд 13Системы уравнений
Система-это несколько уравнений , для которых надо найти общее решение.
Решение
системы - это пара чисел , которая удовлетворяет каждое решение.
Системы равносильны , если имеют одни и те же решения или не имеют их.
Способы решения: 1)Графический
2) Подстановка
3) Сложение
Системы равносильны , если имеют одни и те же решения или не имеют их.
Способы решения: 1)Графический
2) Подстановка
3) Сложение
Слайд 14Система линейных уравнений
а) Если
,то решение одно
б) Если ,то решений бесконечно много
В) Если ,то решений нет
б) Если ,то решений бесконечно много
В) Если ,то решений нет
Слайд 15Неравенства
a>b ,то a-b>0
a
,то a-b=0
Свойства:
1.a>b , то b2.a>b и b>c , то a>c (транзитивность)
3.a>b и c – любое , то a+ c>b+ c
4.a>b и c>0 ,то ac> b c
c<0 , то ac< b c
5.a>b>0 , то
6.a>b>0 , то
Свойства:
1.a>b , то b2.a>b и b>c , то a>c (транзитивность)
3.a>b и c – любое , то a+ c>b+ c
4.a>b и c>0 ,то ac> b c
c<0 , то ac< b c
5.a>b>0 , то
6.a>b>0 , то
Слайд 16Квадратные уравнения
Неприведенное :
,a-I коэффициент , b- II коэффициент , c- свободный член.
Приведенное :
Неполные : и
Решение уравнений
1) с=0 , то , и
2) b=0 ,то
3) , , D= и
4) если b на 2 , то и
Приведенное :
Неполные : и
Решение уравнений
1) с=0 , то , и
2) b=0 ,то
3) , , D= и
4) если b на 2 , то и
Слайд 17Существование корней
1.D>0 -два действительных корня
2.D=0 –два действительных равных
3.D
Теорема Виета
, и
Разложение трехчлена
Слайд 18Квадратные корни
1. ,где
(арифметический)
2. Существует : ,если -да ,если a<0-нет
3. Свойства:
1)
2)
3)
4)
5) , 6)
2. Существует : ,если -да ,если a<0-нет
3. Свойства:
1)
2)
3)
4)
5) , 6)
Слайд 19Действительные числа
Состав
Возможный вид
N= n
Z= m
G=Z или беск.период.дес.др.
J- иррациональные беск.непериод.десят.др.
R=G J всякие десят.др.
N= n
Z= m
G=Z или беск.период.дес.др.
J- иррациональные беск.непериод.десят.др.
R=G J всякие десят.др.
Слайд 20Корни натуральной степени
1.
2. -арифметический
3.Существует: n=2k для ,n=2k+1 для всех a,но один!
4. Свойства
1) 2)
3) 4)
5) 6)
Слайд 21Арифметическая прогрессия
1.
2. Формула
n-го члена :
3. Сумма : или
4. Свойства
2)
1) (среднее арифметическое)
3. Сумма : или
4. Свойства
2)
1) (среднее арифметическое)
Слайд 22Геометрическая прогрессия
1.
2. Формула n-го члена :
3. Сумма : или
4.Свойства :
1)
2) (среднее геометрическое)