- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Платоновы тела и тайна мироздания презентация
Содержание
- 1. Платоновы тела и тайна мироздания
- 2. Великолепная пятерка История правильных многогранников Космический кубок
- 3. ПРАВИЛЬНЫЙ МНОГОГРАННИК - выпуклый многогранник, грани которого
- 4. Правильный тетраэдр Составлен из четырёх
- 5. Составлен из восьми равносторонних треугольников. Каждая вершина
- 6. Правильный икосаэдр Составлен из двадцати равносторонних треугольников.
- 7. Составлен из шести квадратов. Каждая
- 8. Правильный додекаэдр Составлен из двенадцати правильных
- 9. пришли из Древней Греции, в них
- 10. Правильных многогранников вызывающе мало,
- 11. Наш мир исполнен симметрии. С древнейших времен
- 12. Из истории История правильных многогранников уходит
- 13. воды - икосаэдра. Платон связал с правильными
- 14. Однако между двумерным и трехмерным случаями есть
- 15. Евклид вовсе не собирался выпускать систематический учебник
- 16. «Космический кубок» Кеплера Иоганн Кеплер (1571-1630).
- 17. Попытки представить Землю в виде кристаллического тела
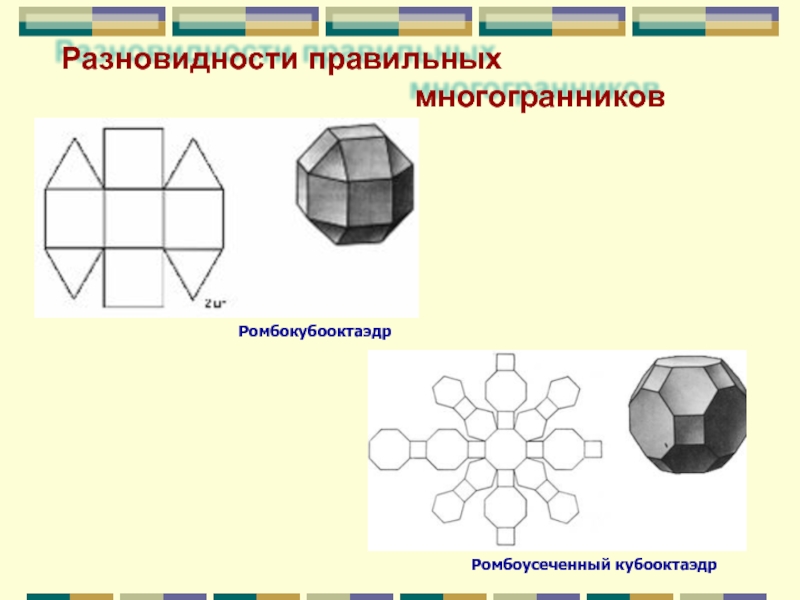
- 18. Ромбоусеченный кубооктаэдр Разновидности правильных
- 19. Для этой модели нужен трафарет – равнобедренный
- 20. Вторая звездчатая форма икосаэдра Тринадцатая звездчатая форма
- 21. Модель можно изготовить, подклеивая треугольные пирамидки к граням икосаэдра Большой звездчатый додекаэдр
- 22. Мауриц Корнелис Эшер (1898–1972) - голландский художник-график.
- 23. Графика Эшера Четыре правильных многогранника
- 24. Сальвадор Дали «Тайная вечеря»
- 25. Вроде бы очень узкое направление у увлечения
- 28. А это просто художественное творчество Елочные игрушки
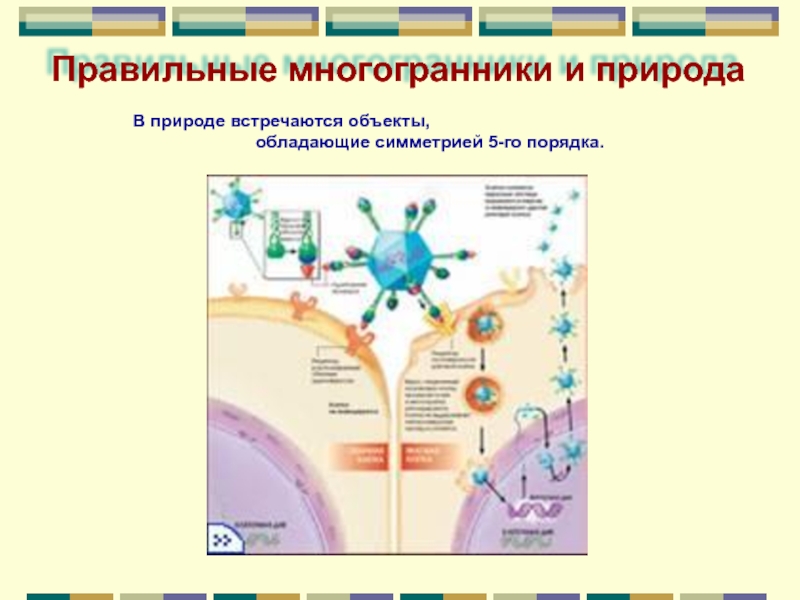
- 29. Правильные многогранники и природа В природе встречаются
- 30. Вирусная частица Аденовирусы - семейство ДНК-
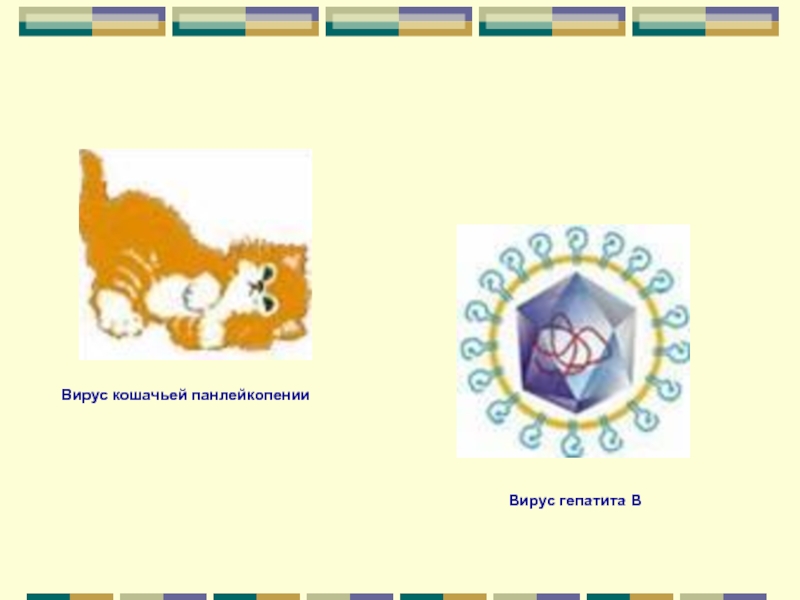
- 31. Вирус кошачьей панлейкопении Вирус гепатита В
- 32. Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр.
- 33. Платины гексафторид (PtF6)- один из сильнейших
- 34. Богатства музея из Средней Сибири приросли самородным
- 35. Два изображения кристаллической решетки галита (поваренной
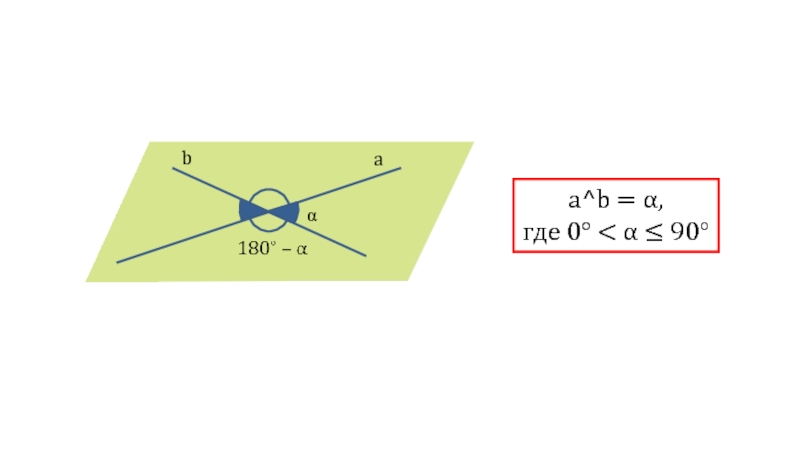
- 36. Симметрия в пространстве
- 37. Симметрия предполагает собой
- 38. Чем дольше мы смотрим на картину, тем
- 39. Симметрия в строительстве
- 40. Дома, утопающие в пышной зелени парка, построены
- 41. Только такой субъект, как гоголевский Собакевич, мог
- 42. Архитектуру называют застывшей музыкой, это не только
- 43. Орнамент в русской архитектуре: изразцовая печь конца XVII — начала XVIII в.
- 44. В Спасе на Крови внутри - умопомрачительно.
- 45. Симметрия встречается не только в объектах, созданных
- 46. Посмотрите на иллюстрации, как вы можете видеть,
- 47. Симметрия в биологии
- 48. Разные образы "телесной симметрии"
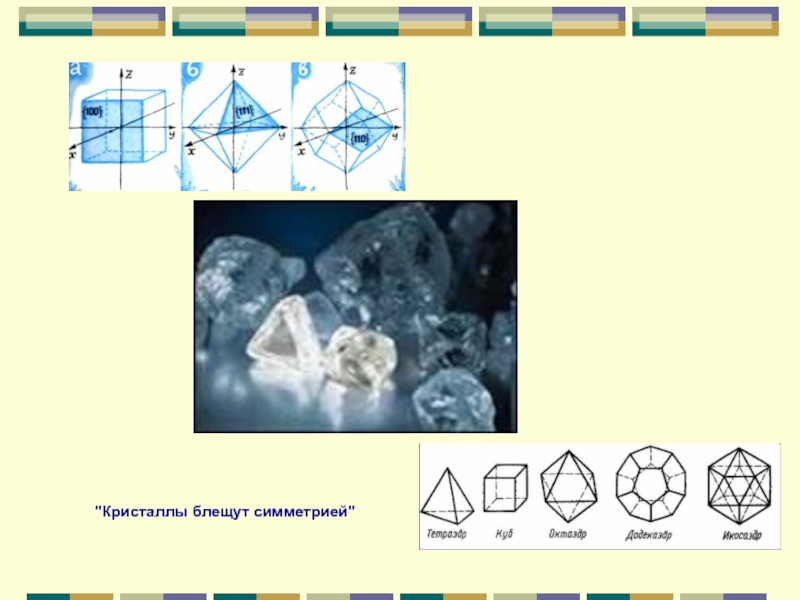
- 49. "Кристаллы блещут симметрией"
- 50. Удивительная симметрия Так пусть же дом и
- 51. Аэродинамическая симметрия Симметрия корпуса Sony VPL-VW100 ось симметрии статора
- 53. Использованные источники и литература
Слайд 2Великолепная пятерка
История правильных многогранников
Космический кубок Кеплера
Разновидности правильных многогранников
Икосаэдро-додекаэдрическая структура Земли
Правильные многогранники,
Правильные многогранники и природа
Симметрия в пространстве
Основополагающий вопрос:
действительно ли мир существует по правилам многогранников?
Слайд 3ПРАВИЛЬНЫЙ МНОГОГРАННИК
- выпуклый многогранник, грани которого являются
правильными многоугольниками с одним
числом сторон и в каждой вершине которого сходится
одно и то же число ребер.
Слайд 4Правильный тетраэдр
Составлен из четырёх равносторонних треугольников. Каждая его вершина
ВЕРШИН: 4 РЕБЕР: 6 ГРАНЕЙ: 4
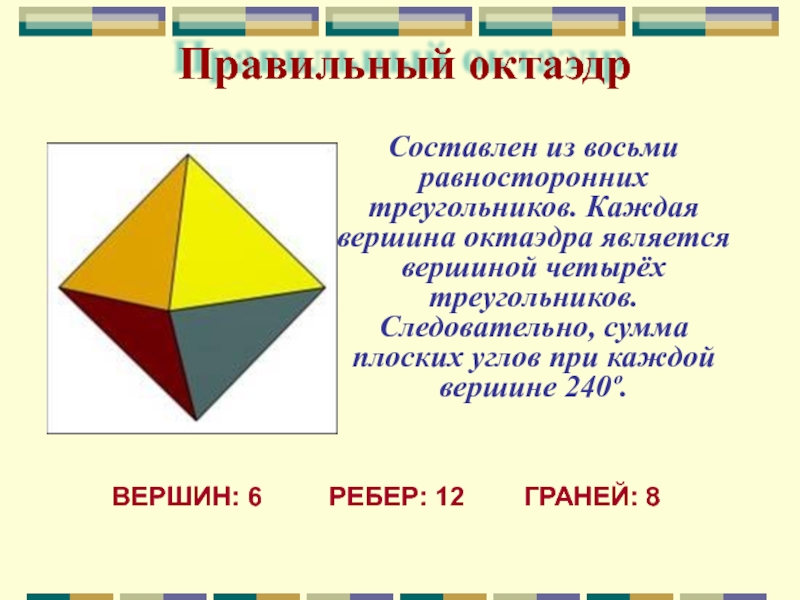
Слайд 5Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх
Правильный октаэдр
ВЕРШИН: 6 РЕБЕР: 12 ГРАНЕЙ: 8
Слайд 6Правильный икосаэдр
Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной
ВЕРШИН: 12 РЕБЕР: 30 ГРАНЕЙ: 20
Слайд 7 Составлен из шести квадратов. Каждая вершина куба является вершиной
Куб (гексаэдр)
ВЕРШИН: 8 РЕБЕР: 12 ГРАНЕЙ: 6
Слайд 8Правильный додекаэдр
Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является
ВЕРШИН: 20 РЕБЕР: 30 ГРАНЕЙ: 12
Слайд 9пришли из Древней Греции,
в них указывается число граней:
«эдра» −
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.
Названия многогранников
Слайд 10 Правильных многогранников вызывающе мало, но этот весьма скромный
Кэрролл Л.
Великолепная пятерка
Слайд 11Наш мир исполнен симметрии. С древнейших времен с ней связаны наши
Слайд 12Из истории
История правильных многогранников уходит в глубокую древность. Правильными многогранниками
Слайд 13воды - икосаэдра.
Платон связал с правильными многогранниками формы атомов основных стихий.
В
атомы огня - форму тетраэдра,
атомы воздуха - октаэдра,
В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным.
Пятый многогранник – додекаэдр символизировал
весь мир и почитался главнейшим.
Платон
(427 – 347 г. до н. э.)
Слайд 14Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно
Платоновы тела - трехмерный аналог плоских правильных многоугольников.
Слайд 15Евклид вовсе не собирался выпускать систематический учебник геометрии. Он задался целью
А.Томпсон.
Одна из легенд рассказывает, что царь Птолемей решил изучить геометрию. Но оказалось, что сделать это не так-то просто. Тогда он призвал Евклида и попросил указать ему легкий путь к математике. "К геометрии нет царской дороги", - ответил ему ученый. Так в виде легенды дошло до нас это ставшее крылатым выражение Евклида
Евклид - древнегреческий
математик (III в до н. э.)
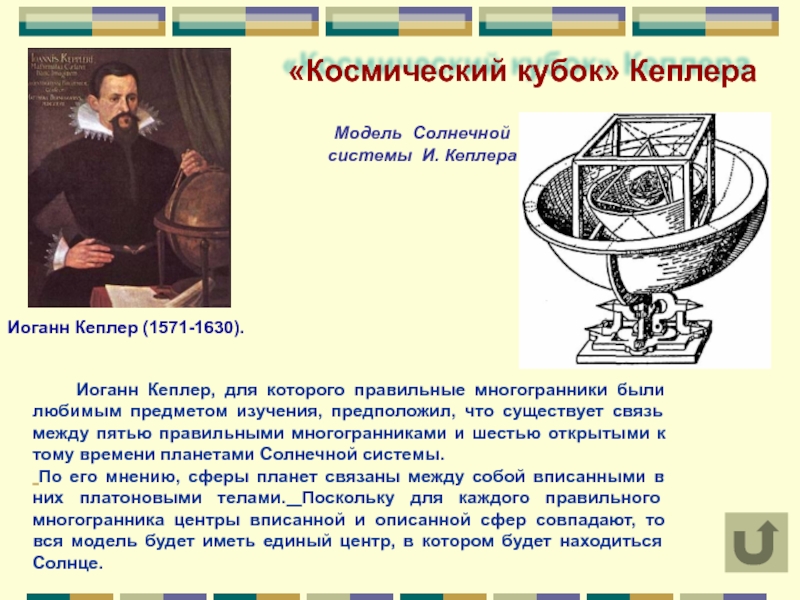
Слайд 16«Космический кубок» Кеплера
Иоганн Кеплер (1571-1630).
Иоганн Кеплер, для которого
По его мнению, сферы планет связаны между собой вписанными в них платоновыми телами. Поскольку для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель будет иметь единый центр, в котором будет находиться Солнце.
Модель Солнечной
системы И. Кеплера
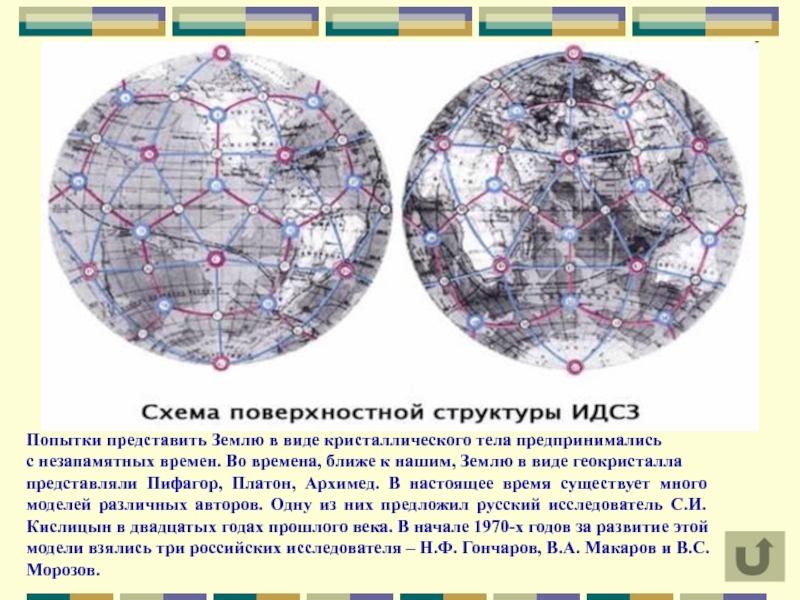
Слайд 17Попытки представить Землю в виде кристаллического тела предпринимались
с незапамятных времен.
представляли Пифагор, Платон, Архимед. В настоящее время существует много моделей различных авторов. Одну из них предложил русский исследователь С.И. Кислицын в двадцатых годах прошлого века. В начале 1970-х годов за развитие этой модели взялись три российских исследователя – Н.Ф. Гончаров, В.А. Макаров и В.С. Морозов.
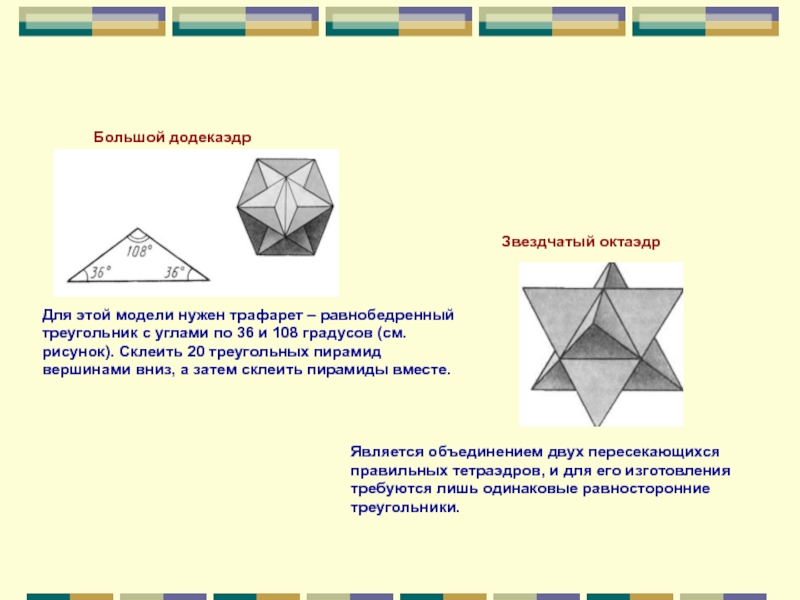
Слайд 19Для этой модели нужен трафарет – равнобедренный треугольник с углами по
Большой додекаэдр
Является объединением двух пересекающихся правильных тетраэдров, и для его изготовления требуются лишь одинаковые равносторонние треугольники.
Звездчатый октаэдр
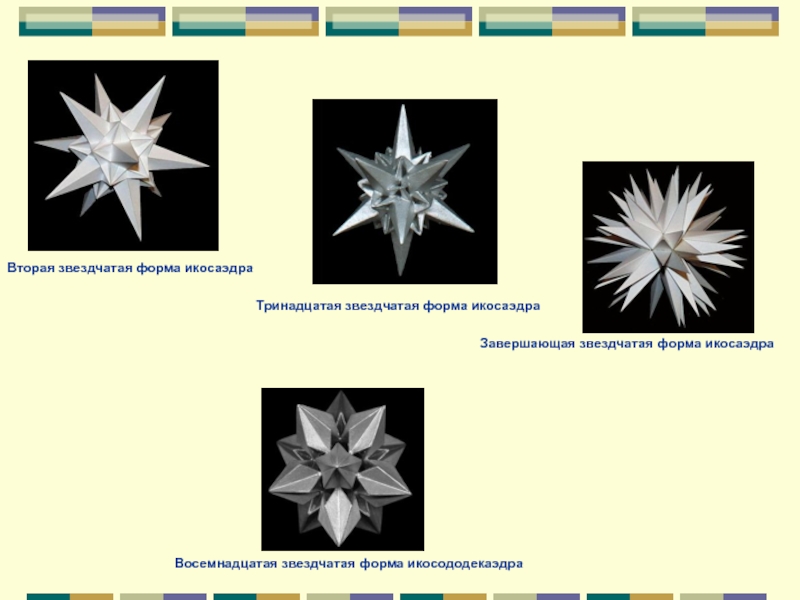
Слайд 20Вторая звездчатая форма икосаэдра
Тринадцатая звездчатая форма икосаэдра
Завершающая звездчатая форма икосаэдра
Восемнадцатая звездчатая
Слайд 21Модель можно изготовить, подклеивая треугольные
пирамидки к граням икосаэдра
Большой звездчатый
Слайд 22Мауриц Корнелис Эшер (1898–1972) - голландский художник-график. С детства проявлял тягу
Правильные геометрические тела - многогранники –имели особое очарование для Эшера. Во многих его работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.
Правильные многогранники,
живопись и скульптура
Слайд 23Графика Эшера
Четыре правильных
многогранника
Изящный пример звездчатого додекаэдра можно найти
Слайд 25Вроде бы очень узкое направление у увлечения этих людей - объемные
Увлечения
Слайд 28А это просто художественное творчество
Елочные игрушки в виде звездчатых
Слайд 29Правильные многогранники и природа
В природе встречаются объекты,
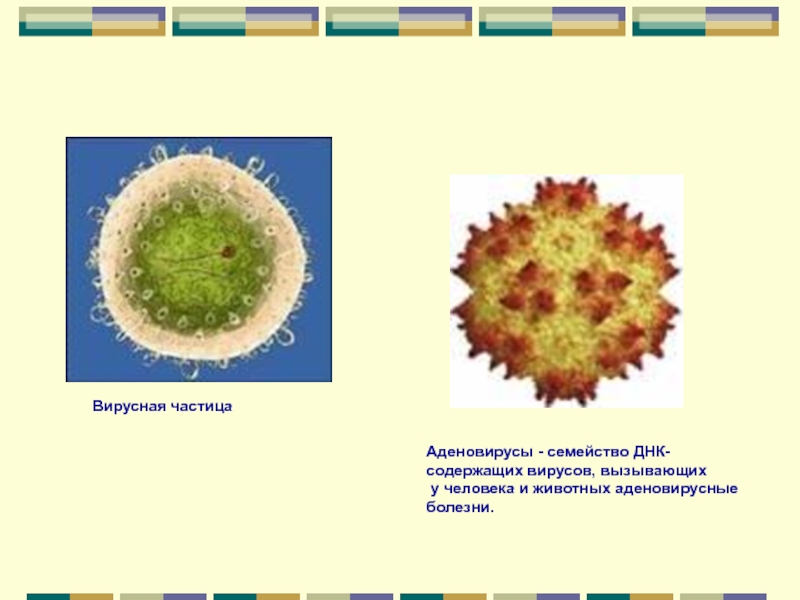
Слайд 30Вирусная частица
Аденовирусы - семейство ДНК-
содержащих вирусов, вызывающих
у человека и
болезни.
Слайд 32Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии
Слайд 33Платины гексафторид (PtF6)-
один из сильнейших окислителей .
Молекула PtF6 - правильный
Молекулярная решетка
в форме октаэдра
Слайд 34Богатства музея из Средней Сибири приросли самородным железом из Хунгтукунской интрузии,
Кристалл пирохлора в форме октаэдра
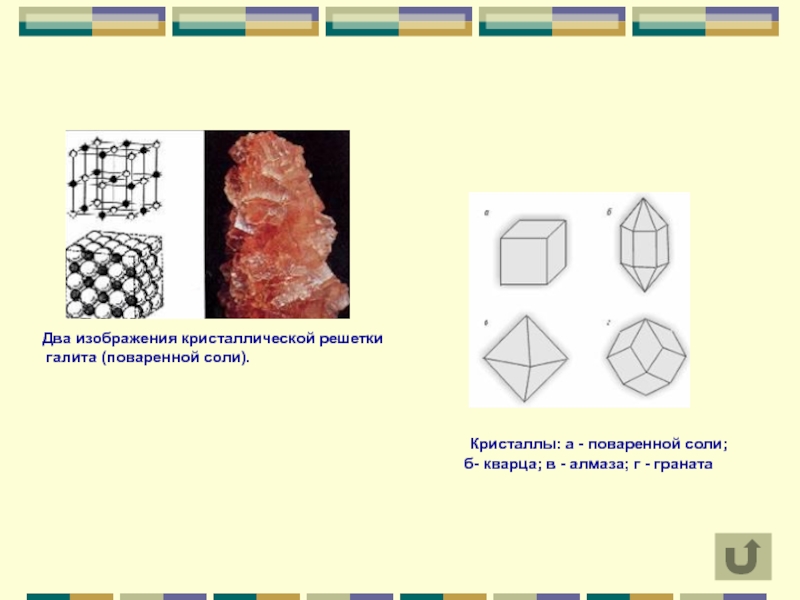
Слайд 35Два изображения кристаллической решетки
галита (поваренной соли).
Кристаллы: а - поваренной
б- кварца; в - алмаза; г - граната
Слайд 37
Симметрия предполагает собой некий определенный порядок,
математическую закономерность расположения элементов
относительно друг друга и в пространстве.
Слайд 38Чем дольше мы смотрим на картину, тем сильнее погружаемся в ее
Слайд 40Дома, утопающие в пышной зелени парка, построены в стиле русского усадебного
Слайд 41Только такой субъект, как гоголевский Собакевич, мог вступить в спор с
Слайд 42Архитектуру называют застывшей музыкой, это не только красивая
метафора, но в
Мавзолей Саманидов в Бухаре.
Схема пропорций по П. Захидову
Слайд 44В Спасе на Крови внутри - умопомрачительно. огромнейшее пространство храма и
Храм впечатляет как снаружи, так и изнутри.
Слайд 45Симметрия встречается не только в объектах, созданных человеком, мы сплошь и
Слайд 46Посмотрите на иллюстрации, как вы можете видеть, в природе не бывает
Слайд 50Удивительная симметрия
Так пусть же дом и сад,
Аллеи и лужайки
Доставят сладостный
Своей хозяйке
Ж. Делиль
Слайд 52
Правильные многогранники - удивительные символы симметрии, привлекавшие внимание множества выдающихся мыслителей;
правильные многогранники – фигуры, обладающие всеми тремя видами симметрии: центральной, осевой и зеркальной, и поэтому особенно интересны для изучения и восхищения;
что красиво и полезно, то и выгодно, (пример с формой вирусов). Но, конечно, природа разнообразна. Поэтому говорить о том, что мир живет только по законам многогранников – это неверно;
красота и гармония тесно связаны с симметрией, это подметили еще древние архитекторы и художники. Пропорция и симметрия объекта всегда необходимы нашему зрительному восприятию для того, чтобы мы могли считать этот объект красивым.