- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Джон Непер презентация
Содержание
- 1. Джон Непер
- 2. Джон Непер Шотландский математик -изобретатель логарифмов.
- 3. План: Определение. Свойства. Десятичные и натуральные логарифмы.
- 4. Определение логарифма: Логарифмом положительного числа b по
- 5. Свойства логарифмов: Loga(bc)=logab+ logac Loga (b/с)= logab-logac
- 6. Десятичные и натуральные логарифмы: Десятичным логарифмом числа
- 7. Логарифмическая функция. Логарифмическая функция: y=logax
- 8. Логарифмическая функция и её график: y
- 9. Логарифмические уравнения Решить уравнение:
- 10. Решение систем: Решить систему уравнений: log2x
- 11. Логарифмические неравенства: Решить неравенство: log2(x-3)
Джон Непер Шотландский математик -изобретатель логарифмов. В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый
Слайд 2Джон Непер
Шотландский математик -изобретатель логарифмов.
В 1590-х годах пришел к идее логарифмических вычислений и составил первые таблицы логарифмов, однако свой знаменитый труд “Описание удивительных таблиц логарифмов” опубликовал лишь в 1614 году.
Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
Ему принадлежит определение логарифмов, объяснение их свойств, таблицы логарифмов синусов, косинусов, тангенсов и приложения логарифмов в сферической тригонометрии.
Слайд 3План:
Определение.
Свойства.
Десятичные и натуральные логарифмы.
Логарифмическая функция, ее свойства и график.
Решение логарифмических уравнений
и неравенств.
Слайд 4Определение логарифма:
Логарифмом положительного числа b по основанию a, где a>0, a≠1,
называется показатель степени, в которую надо возвести число a, чтобы получить b.
Основное логарифмическое тождество:
alogab= b, где b>0, a>0
Действие нахождения логарифма называется логарифмированием.
Основное логарифмическое тождество:
alogab= b, где b>0, a>0
Действие нахождения логарифма называется логарифмированием.
Слайд 5Свойства логарифмов:
Loga(bc)=logab+ logac
Loga (b/с)= logab-logac
Logabr=rlogab
Logab=logcb/logca
Logab=1/logba
alogbc= clogba
Logarb=1/r logab
alogab= b
Слайд 6Десятичные и натуральные логарифмы:
Десятичным логарифмом числа называют логарифм этого числа по
основанию 10. Записывается lgb
Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e-иррациональное число, приближенно равное 2,7. При этом записывается lnb
Натуральным логарифмом числа называют логарифм этого числа по основанию e, где e-иррациональное число, приближенно равное 2,7. При этом записывается lnb
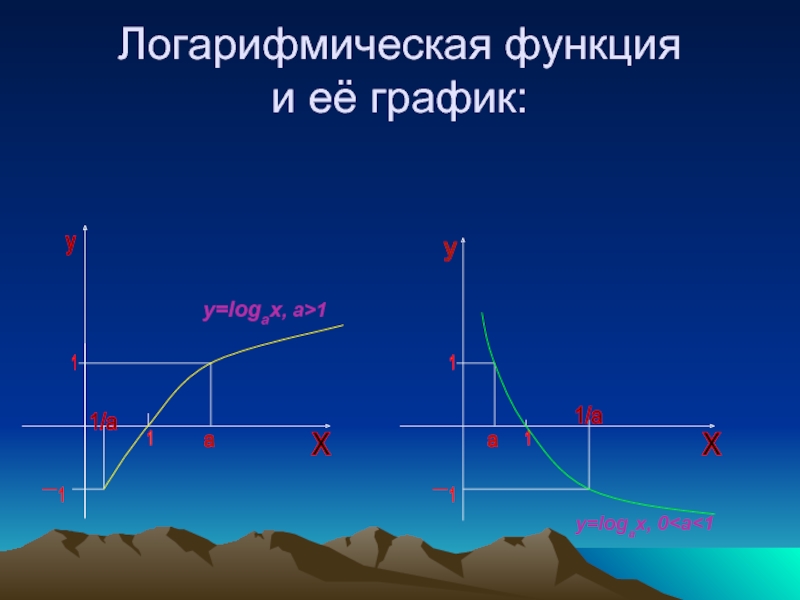
Слайд 7Логарифмическая функция.
Логарифмическая функция: y=logax
Свойства:
Множество значений логарифмической функции -множество всех положительных чисел
Множество значений логарифмической функции-множество R всех действительных чисел.
Логарифмическая функция y=logax является возрастающей на промежутке x>0, если a>1, и убывающей, если 0Если a>1, то функция y=logax принимает положительные значения при x>1, отрицательные при 01.
Логарифмическая функция y=logax и показательная функция y=ax, где a>0, a≠1, взаимно обратны.
Множество значений логарифмической функции -множество всех положительных чисел
Множество значений логарифмической функции-множество R всех действительных чисел.
Логарифмическая функция y=logax является возрастающей на промежутке x>0, если a>1, и убывающей, если 0
Логарифмическая функция y=logax и показательная функция y=ax, где a>0, a≠1, взаимно обратны.
Слайд 8Логарифмическая функция
и её график:
y
y
1
1
a
a
1
-
1/a
1
1/a
1
-
1
x
x
y=logax, 0 y=logax, a>1
Слайд 9Логарифмические уравнения
Решить уравнение:
Log2(x+1)+ Log2(x+3)=3
Решение:
Используя свойство логарифма, получаем:
Log2(x+1)(x+3)=3
Из этого равенства по определению логарифма получаем:
(x+1)(x+3)=8.
Теперь раскроем скобки и решим квадратное уравнение x2+4x-5=0, откуда x1=1, x2=-5
При X2=-5 числа (x+1 и x+3)<0, следовательно x=-5 не является корнем уравнения.
Ответ. X=1
Используя свойство логарифма, получаем:
Log2(x+1)(x+3)=3
Из этого равенства по определению логарифма получаем:
(x+1)(x+3)=8.
Теперь раскроем скобки и решим квадратное уравнение x2+4x-5=0, откуда x1=1, x2=-5
При X2=-5 числа (x+1 и x+3)<0, следовательно x=-5 не является корнем уравнения.
Ответ. X=1
Слайд 10Решение систем:
Решить систему уравнений:
log2x - log2y = 1,
4y2 +x
- 12= 0.
Решение:
Из первого уравнения выразим x через y:
log2 x/y=log22, x/y=2, x=2y. Подставив x=2y во второе уравнение системы, получим 4y2 +2y – 12=0, откуда y1=3/2, y2=-2. Найдем значения x: x1=3, x2=-4. Проверка показывает, что -4 и -2 – постороннее решение.
Ответ. X=3, y=3/2.
Слайд 11Логарифмические неравенства:
Решить неравенство:
log2(x-3) + log2(x-2) ≤ 1
Решение:
О.о. X>3.
Используя свойства логарифма, получаем:
log2(x-3) (x-2) ≤ log22. Логарифмическая функция с основанием 2 является возрастающей, поэтому при x>3 неравенство log2(x-3) (x-2) ≤ log22 выполняется при (x-3)(x-2)≤2. Это неравенство можно записать в виде системы уравнений:
(x-3)(x-2) ≤2
X>3
/////////////// ///////
0 1 3 4
О.о. X>3.
Используя свойства логарифма, получаем:
log2(x-3) (x-2) ≤ log22. Логарифмическая функция с основанием 2 является возрастающей, поэтому при x>3 неравенство log2(x-3) (x-2) ≤ log22 выполняется при (x-3)(x-2)≤2. Это неравенство можно записать в виде системы уравнений:
(x-3)(x-2) ≤2
X>3
/////////////// ///////
0 1 3 4
XXXX
x
Швецов Руслан Иб-12
