- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перпендикулярность прямых и плоскостей презентация
Содержание
- 1. Перпендикулярность прямых и плоскостей
- 2. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
- 3. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ Прямая называется перпендикулярной
- 4. Докажите, что плоскость, проходящая через ребро AB
- 5. Докажите, что прямая AA1, проходящая через вершины
- 6. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ Пусть дана плоскость π
- 7. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ Наклонной к плоскости называется
- 8. Дано: α АС ⊥ α; С ∈
- 9. Установить взаимное положение прямых а и
- 10. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Две плоскости называются перпендикулярными, если
- 11. б) AВB1, CDD1, AB1C1. В кубе A…D1
- 12. ДВУГРАННЫЙ УГОЛ Двугранным углом называется фигура (рис.
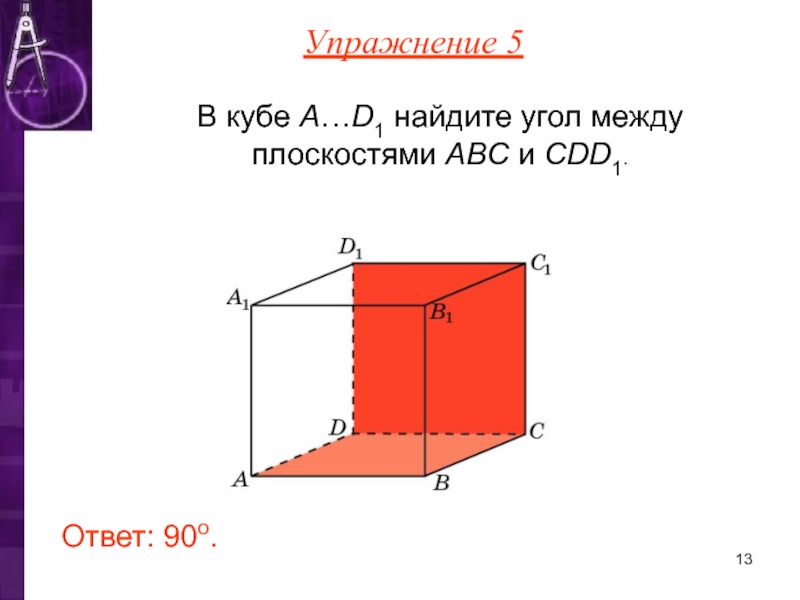
- 13. В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ: 90o. Упражнение 5
- 14. В кубе A…D1 найдите угол между плоскостями ABC и CDA1. Ответ: 45o. Упражнение 6
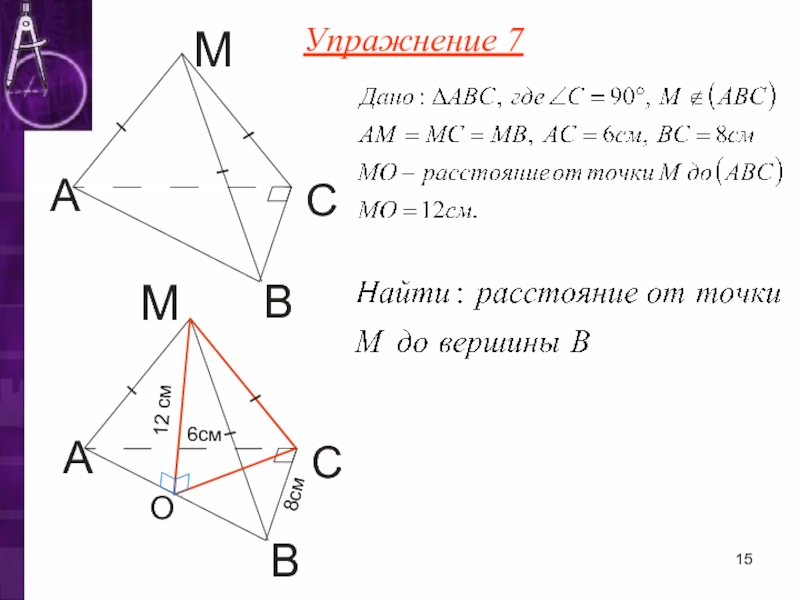
- 15. Упражнение 7
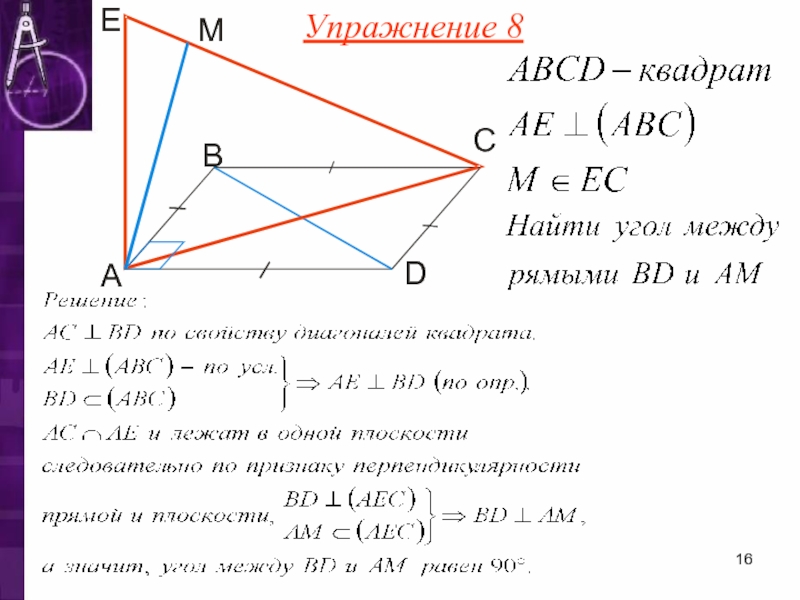
- 16. Упражнение 8
- 17. Точка М равноудалена от всех вершин правильного
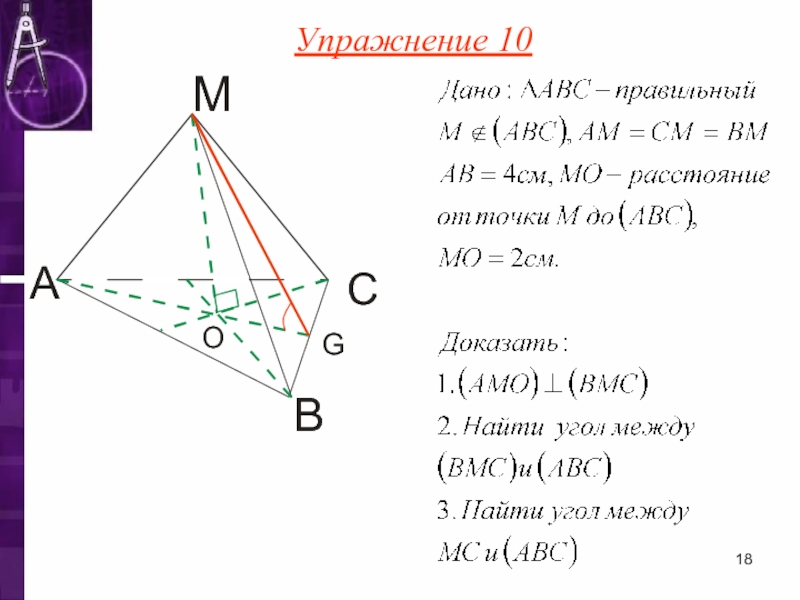
- 18. Упражнение 10
Слайд 2ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
ДВУГРАННЫЙ УГОЛ
РЕШЕНИЕ
План:
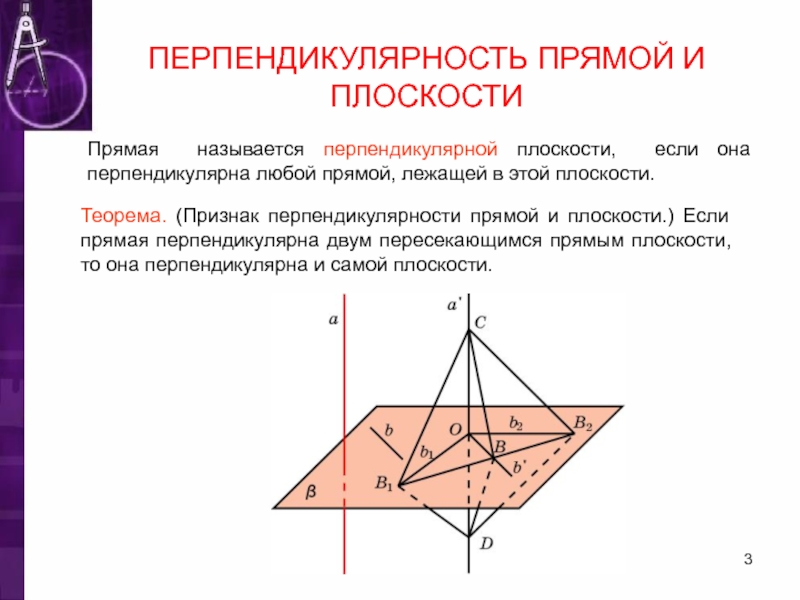
Слайд 3ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой
Теорема. (Признак перпендикулярности прямой и плоскости.) Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости.
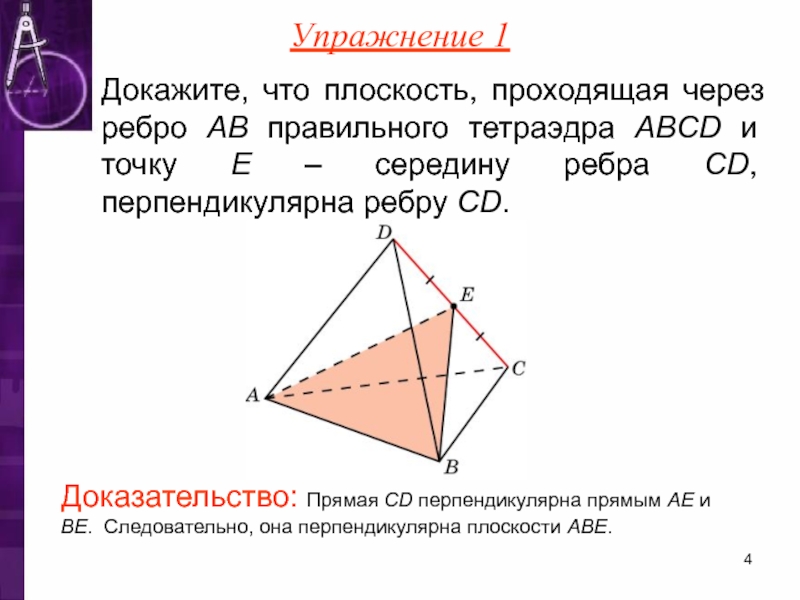
Слайд 4Докажите, что плоскость, проходящая через ребро AB правильного тетраэдра ABCD и
Упражнение 1
Доказательство: Прямая CD перпендикулярна прямым AE и BE. Следовательно, она перпендикулярна плоскости ABE.
Слайд 5 Докажите, что прямая AA1, проходящая через вершины куба ABCDA1B1C1D1 перпендикулярна плоскости
Доказательство. Прямая AA1 перпендикулярна прямым AB и AD. Следовательно, она перпендикулярна плоскости ABC.
Упражнение 2
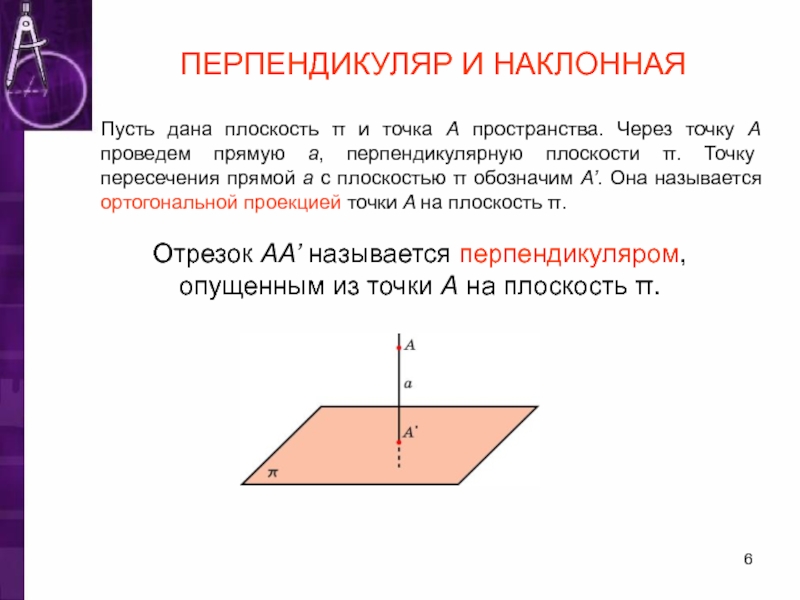
Слайд 6ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Пусть дана плоскость π и точка A пространства. Через
Отрезок AA’ называется перпендикуляром, опущенным из точки A на плоскость π.
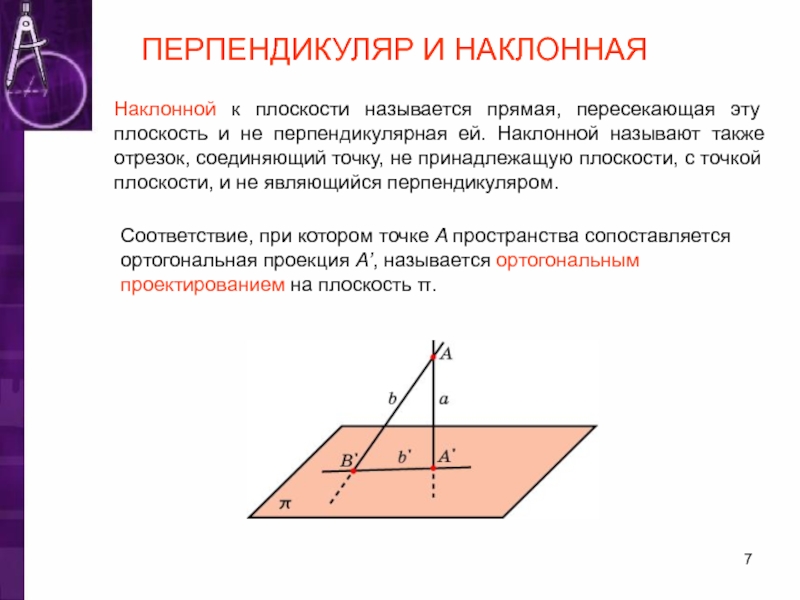
Слайд 7ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
Наклонной к плоскости называется прямая, пересекающая эту плоскость и
Соответствие, при котором точке A пространства сопоставляется ортогональная проекция A’, называется ортогональным проектированием на плоскость π.
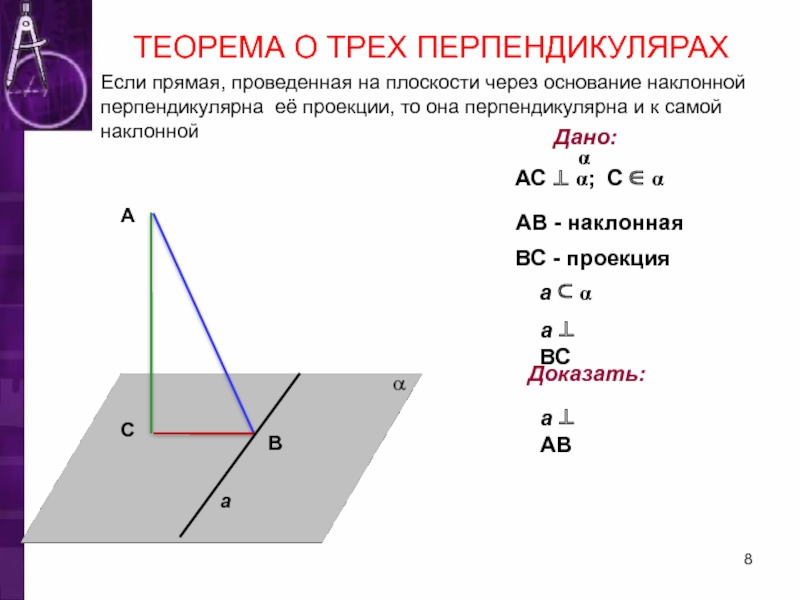
Слайд 8Дано:
α
АС ⊥ α; С ∈ α
АВ - наклонная
ВС - проекция
a
a ⊥ ВС
Доказать:
a ⊥ АВ
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
Если прямая, проведенная на плоскости через основание наклонной перпендикулярна её проекции, то она перпендикулярна и к самой наклонной
Слайд 9
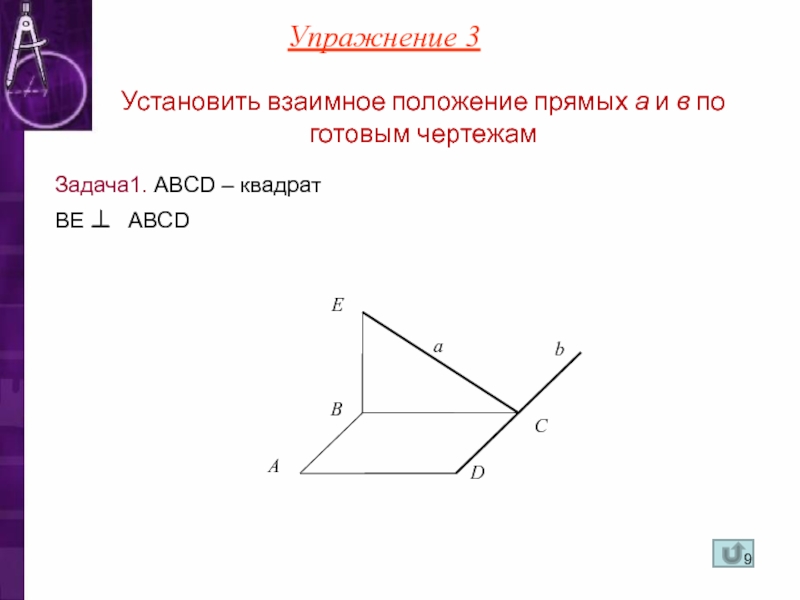
Установить взаимное положение прямых а и в по готовым чертежам
Задача1.
BE ⊥ ABCD
A
b
a
C
B
D
E
Упражнение 3
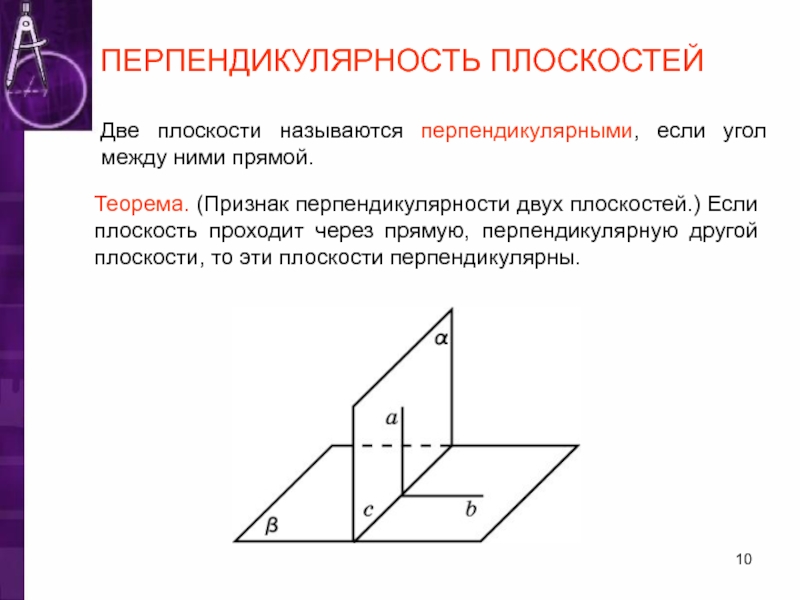
Слайд 10ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ
Две плоскости называются перпендикулярными, если угол между ними прямой.
Теорема. (Признак
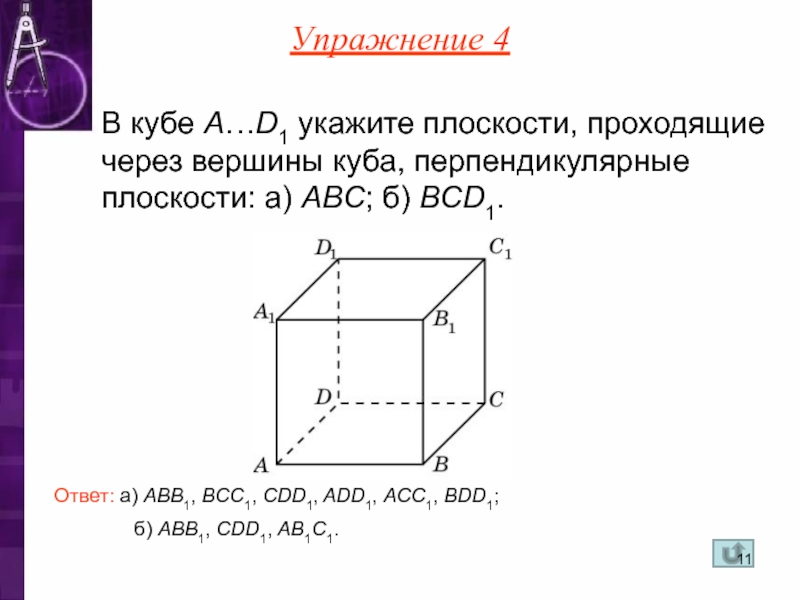
Слайд 11б) AВB1, CDD1, AB1C1.
В кубе A…D1 укажите плоскости, проходящие через вершины
Ответ: а) ABB1, BCC1, CDD1, ADD1, ACC1, BDD1;
Упражнение 4
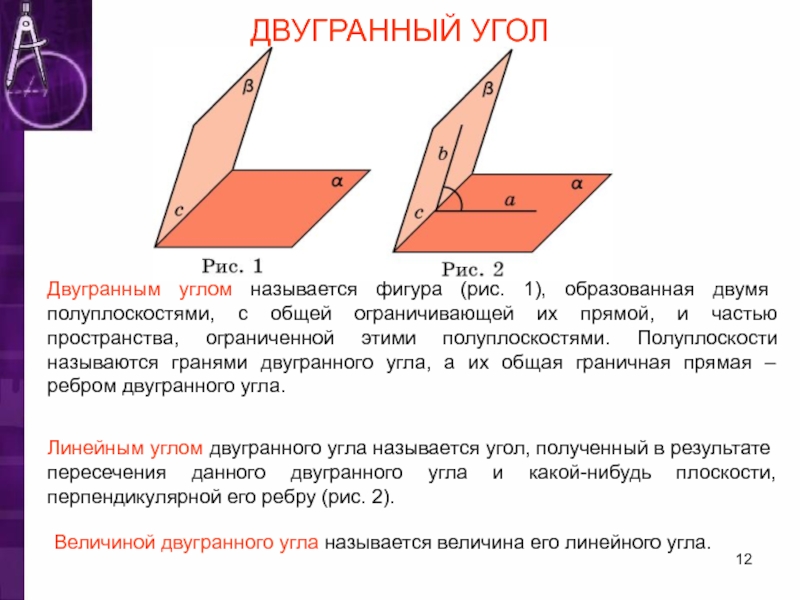
Слайд 12ДВУГРАННЫЙ УГОЛ
Двугранным углом называется фигура (рис. 1), образованная двумя полуплоскостями, с
Линейным углом двугранного угла называется угол, полученный в результате пересечения данного двугранного угла и какой-нибудь плоскости, перпендикулярной его ребру (рис. 2).
Величиной двугранного угла называется величина его линейного угла.
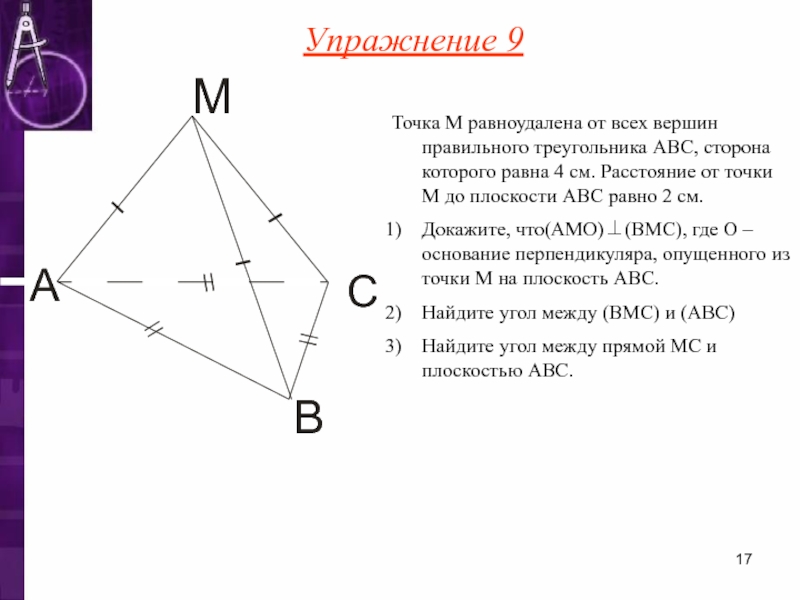
Слайд 17Точка М равноудалена от всех вершин правильного треугольника ABC, сторона которого
Докажите, что(AMO)⊥(BMC), где O – основание перпендикуляра, опущенного из точки М на плоскость ABC.
Найдите угол между (BMC) и (ABC)
Найдите угол между прямой MC и плоскостью ABC.
Упражнение 9