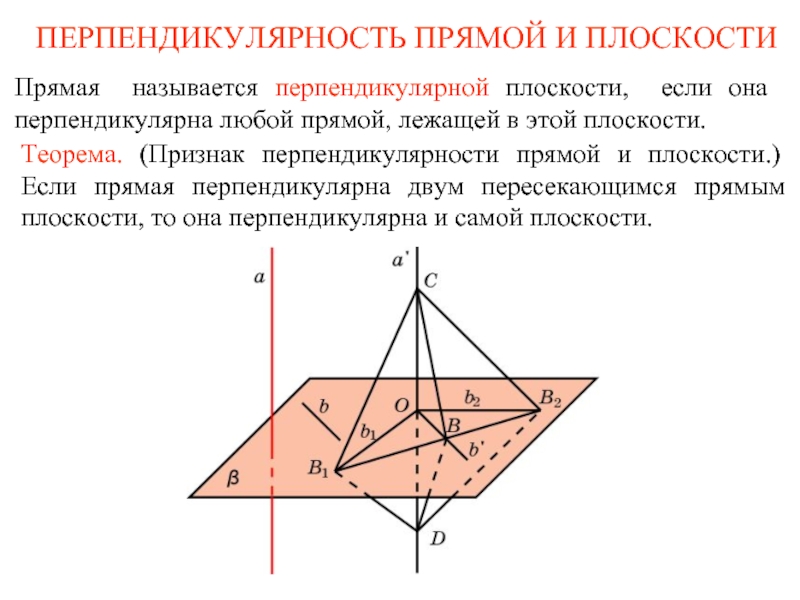
Теорема. (Признак перпендикулярности прямой и плоскости.) Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна и самой плоскости.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перпендикулярность прямой и плоскости презентация
Содержание
- 1. Перпендикулярность прямой и плоскости
- 2. Верно ли, что если прямая перпендикулярна каким-нибудь
- 3. Прямая параллельна плоскости. Может ли она быть
- 4. Что представляет собой геометрическое место точек, расположенных
- 5. Как расположена относительно плоскости треугольника прямая, перпендикулярная двум его сторонам? Ответ: Перпендикулярна. Упражнение 4
- 6. Найдите ГМТ в пространстве, равноудалённых от двух
- 7. При каком взаимном расположении двух прямых через
- 8. Определите вид треугольника, если через одну из
- 9. Докажите, что плоскость, проходящая через ребро AB
- 10. Докажите, что отрезок EF, соединяющий середины противоположных
- 11. Докажите, что прямая SO, проходящая через вершину
- 12. Докажите, что прямая SO, проходящая через вершину
- 13. Докажите, что прямая AC, проходящая через вершины
- 14. Докажите, что прямая AA1, проходящая через вершины
- 15. Докажите, что прямые AA1 и BD, проходящие
- 16. Докажите, что прямая BD, проходящая через вершины
- 17. Докажите, что прямые CA1 и BD, проходящие через вершины куба ABCDA1B1C1D1, перпендикулярны. Упражнение 16
- 18. б) AB, CD, A1B1, C1D1; В кубе
- 19. б) BCD1. В кубе ABCDA1B1C1D1 укажите плоскости,
- 20. Сколько имеется пар перпендикулярных прямых и плоскостей,
- 21. Докажите, что прямая AA1, проходящая через вершины
- 22. Докажите, что прямая AA1, проходящая через вершины
- 23. Докажите, что прямая AB, проходящая через вершины
- 24. Докажите, что прямая BD, проходящая через вершины
- 25. Докажите, что прямая CF, проходящая через вершины
- 26. Докажите, что прямая AC, проходящая через вершины
- 27. Докажите, что прямая AB1, проходящая через вершины
- 28. В правильной шестиугольной призме назовите плоскости, проходящие
- 29. В правильной шестиугольной призме назовите прямые, проходящие
- 30. Назовите прямые, проходящие через вершины многогранника, изображенного
- 31. Назовите прямые, проходящие через вершины многогранника, изображенного
Верно ли, что если прямая перпендикулярна каким-нибудь двум прямым плоскости, то она перпендикулярна этой плоскости? Ответ: Нет. Упражнение 1
Слайд 1ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой
прямой, лежащей в этой плоскости.
Слайд 2Верно ли, что если прямая перпендикулярна каким-нибудь двум прямым плоскости, то
она перпендикулярна этой плоскости?
Ответ: Нет.
Упражнение 1
Слайд 3Прямая параллельна плоскости. Может ли она быть перпендикулярной какой-нибудь прямой, лежащей
в этой плоскости?
Ответ: Да.
Упражнение 2
Слайд 4Что представляет собой геометрическое место точек, расположенных на прямых, проходящих через
данную точку на прямой и перпендикулярных этой прямой?
Ответ: Плоскость, перпендикулярная данной прямой.
Упражнение 3
Слайд 5Как расположена относительно плоскости треугольника прямая, перпендикулярная двум его сторонам?
Ответ: Перпендикулярна.
Упражнение
4
Слайд 6Найдите ГМТ в пространстве, равноудалённых от двух данных точек.
Ответ: Плоскость, проходящая
через середину отрезка, концами которого являются данные точки, и перпендикулярная этому отрезку.
Упражнение 5
Слайд 7При каком взаимном расположении двух прямых через одну из них можно
провести плоскость, перпендикулярную другой?
Ответ: Прямые перпендикулярны.
Упражнение 6
Слайд 8Определите вид треугольника, если через одну из его сторон можно провести
плоскость, перпендикулярную другой стороне.
Ответ: Прямоугольный.
Упражнение 7
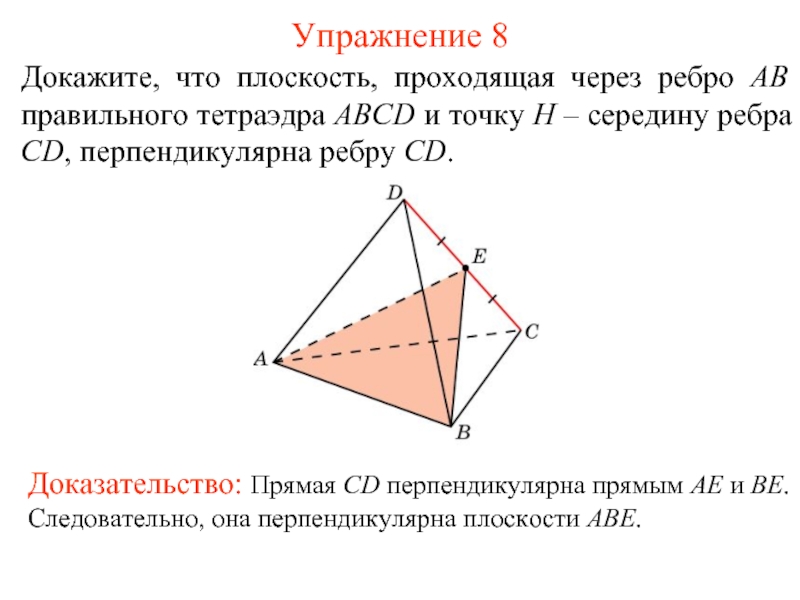
Слайд 9Докажите, что плоскость, проходящая через ребро AB правильного тетраэдра ABCD и
точку H – середину ребра CD, перпендикулярна ребру CD.
Упражнение 8
Доказательство: Прямая CD перпендикулярна прямым AE и BE. Следовательно, она перпендикулярна плоскости ABE.
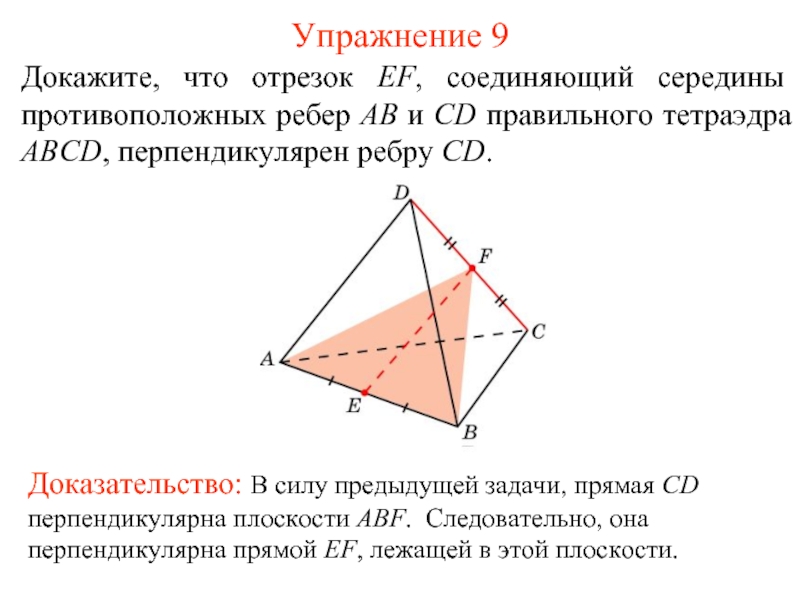
Слайд 10Докажите, что отрезок EF, соединяющий середины противоположных ребер AB и CD
правильного тетраэдра ABCD, перпендикулярен ребру CD.
Упражнение 9
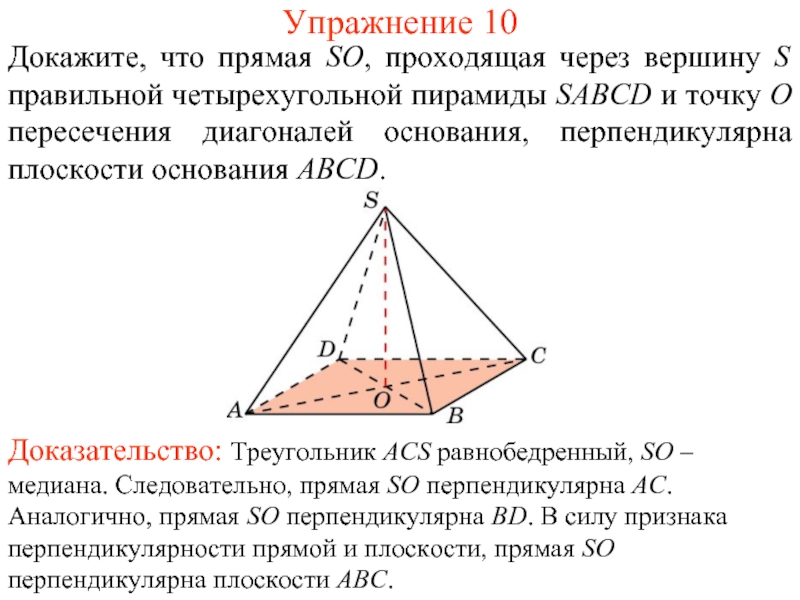
Слайд 11Докажите, что прямая SO, проходящая через вершину S правильной четырехугольной пирамиды
SABCD и точку O пересечения диагоналей основания, перпендикулярна плоскости основания ABCD.
Упражнение 10
Доказательство: Треугольник ACS равнобедренный, SO – медиана. Следовательно, прямая SO перпендикулярна AC. Аналогично, прямая SO перпендикулярна BD. В силу признака перпендикулярности прямой и плоскости, прямая SO перпендикулярна плоскости ABC.
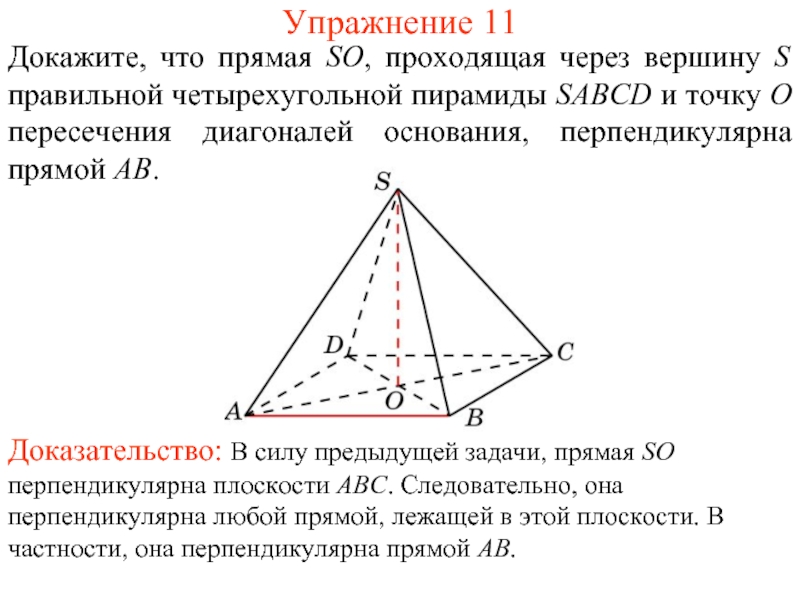
Слайд 12Докажите, что прямая SO, проходящая через вершину S правильной четырехугольной пирамиды
SABCD и точку O пересечения диагоналей основания, перпендикулярна прямой AB.
Упражнение 11
Доказательство: В силу предыдущей задачи, прямая SO перпендикулярна плоскости ABC. Следовательно, она перпендикулярна любой прямой, лежащей в этой плоскости. В частности, она перпендикулярна прямой AB.
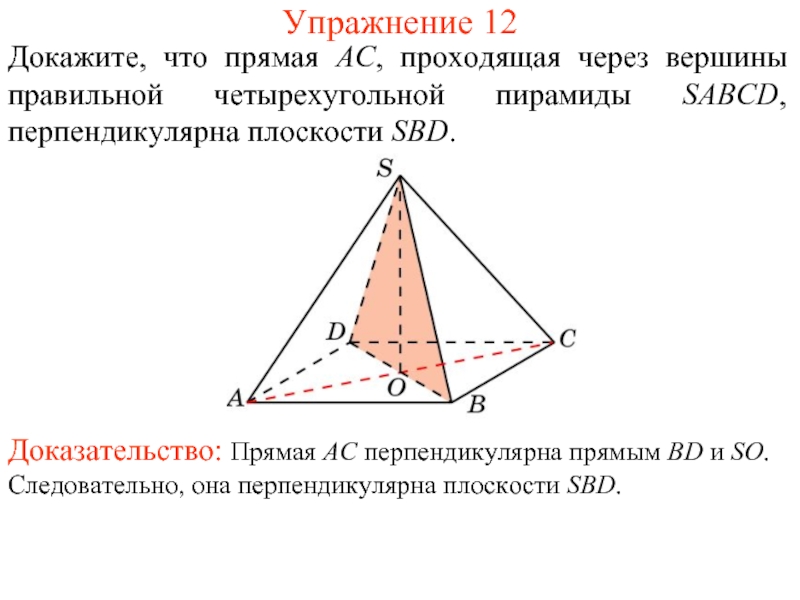
Слайд 13Докажите, что прямая AC, проходящая через вершины правильной четырехугольной пирамиды SABCD,
перпендикулярна плоскости SBD.
Упражнение 12
Доказательство: Прямая AC перпендикулярна прямым BD и SO. Следовательно, она перпендикулярна плоскости SBD.
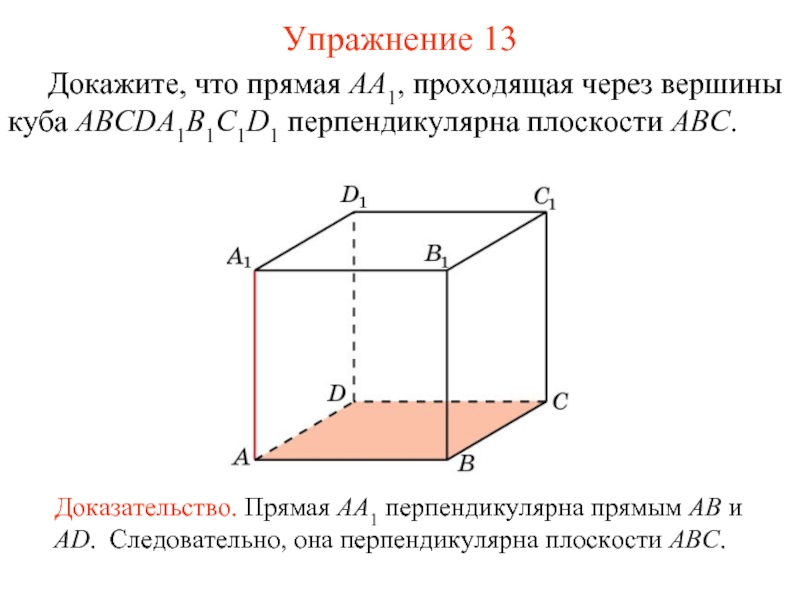
Слайд 14 Докажите, что прямая AA1, проходящая через вершины куба ABCDA1B1C1D1 перпендикулярна плоскости
ABC.
Доказательство. Прямая AA1 перпендикулярна прямым AB и AD. Следовательно, она перпендикулярна плоскости ABC.
Упражнение 13
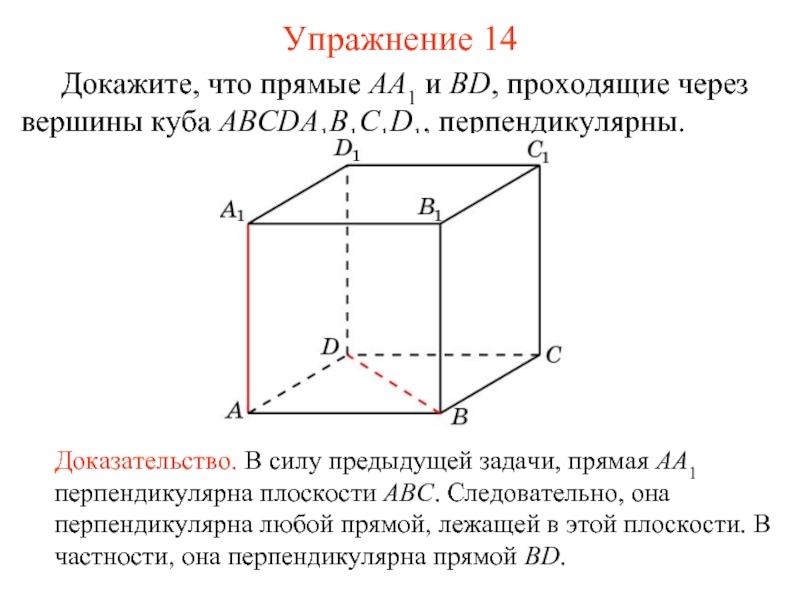
Слайд 15 Докажите, что прямые AA1 и BD, проходящие через вершины куба ABCDA1B1C1D1,
перпендикулярны.
Доказательство. В силу предыдущей задачи, прямая AA1 перпендикулярна плоскости ABC. Следовательно, она перпендикулярна любой прямой, лежащей в этой плоскости. В частности, она перпендикулярна прямой BD.
Упражнение 14
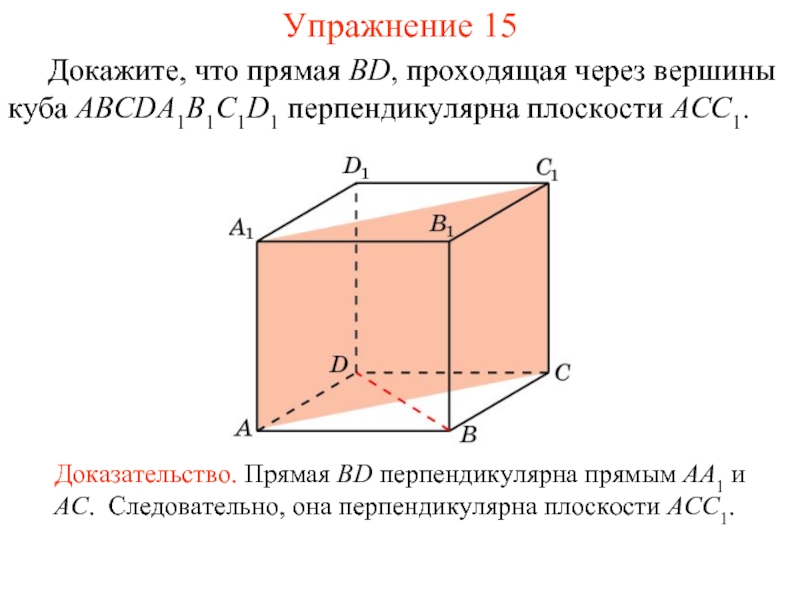
Слайд 16 Докажите, что прямая BD, проходящая через вершины куба ABCDA1B1C1D1 перпендикулярна плоскости
ACC1.
Доказательство. Прямая BD перпендикулярна прямым AA1 и AC. Следовательно, она перпендикулярна плоскости ACC1.
Упражнение 15
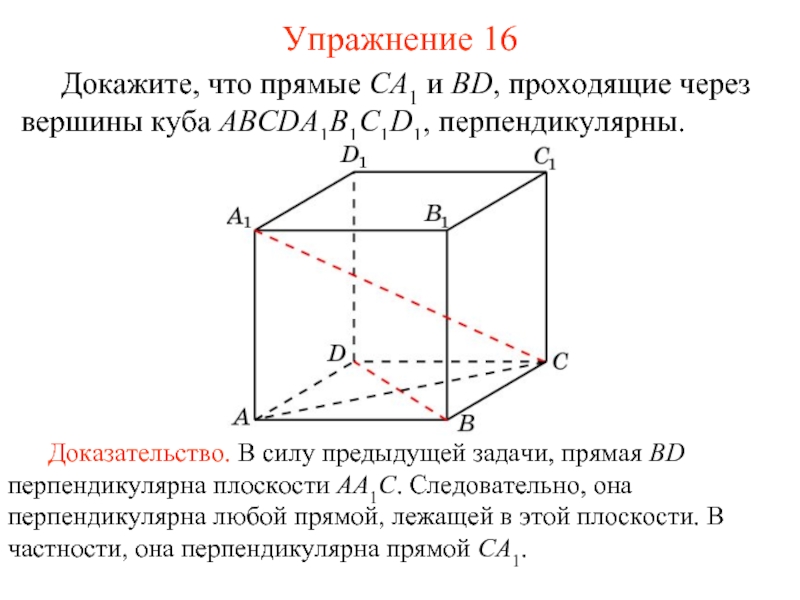
Слайд 17 Докажите, что прямые CA1 и BD, проходящие через вершины куба ABCDA1B1C1D1,
перпендикулярны.
Упражнение 16
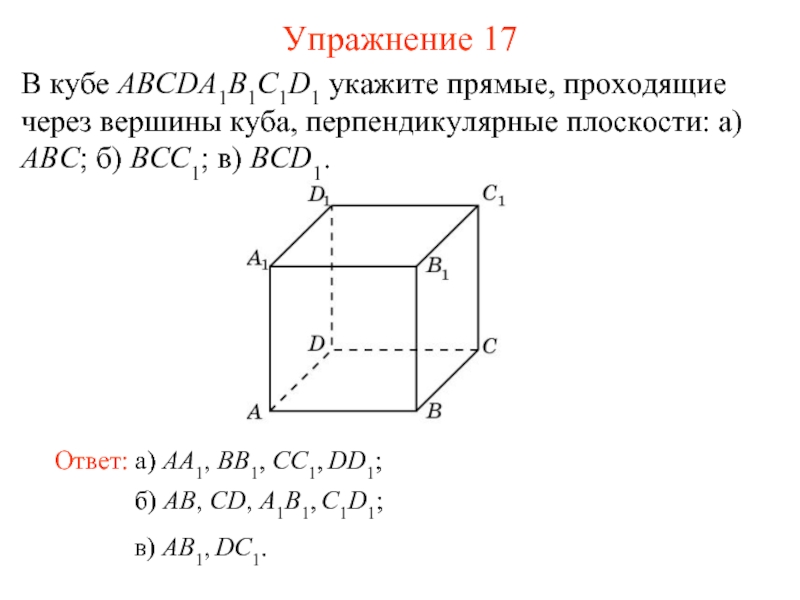
Слайд 18б) AB, CD, A1B1, C1D1;
В кубе ABCDA1B1C1D1 укажите прямые, проходящие через
вершины куба, перпендикулярные плоскости: а) ABC; б) BCC1; в) BCD1.
Ответ: а) AA1, BB1, CC1, DD1;
Упражнение 17
в) AB1, DC1.
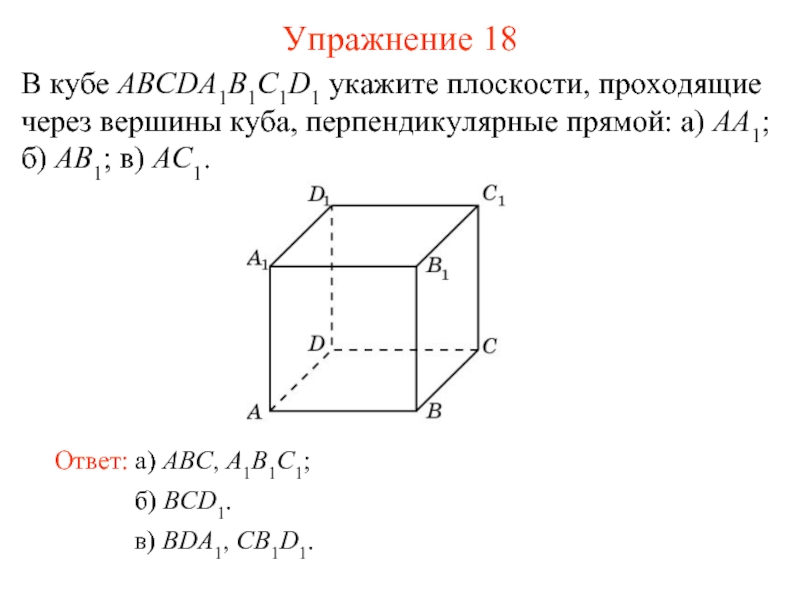
Слайд 19б) BCD1.
В кубе ABCDA1B1C1D1 укажите плоскости, проходящие через вершины куба, перпендикулярные
прямой: а) AA1; б) AB1; в) AC1.
Ответ: а) ABC, A1B1C1;
Упражнение 18
в) BDA1, CB1D1.
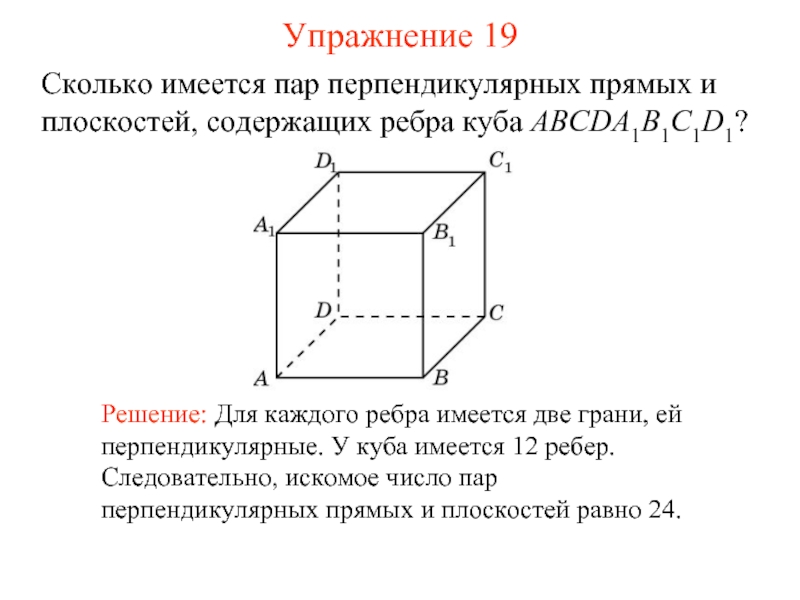
Слайд 20Сколько имеется пар перпендикулярных прямых и плоскостей, содержащих ребра куба ABCDA1B1C1D1?
Решение: Для каждого ребра имеется две грани, ей перпендикулярные. У куба имеется 12 ребер. Следовательно, искомое число пар перпендикулярных прямых и плоскостей равно 24.
Упражнение 19
Слайд 21 Докажите, что прямая AA1, проходящая через вершины правильной треугольной призмы ABCA1B1C1,
перпендикулярна плоскости ABC.
Доказательство. Прямая AA1 перпендикулярна прямым AB и AC. Следовательно, она перпендикулярна плоскости ABC.
Упражнение 20
Слайд 22Докажите, что прямая AA1, проходящая через вершины правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
перпендикулярна плоскости ABC.
Доказательство. Прямая AA1 перпендикулярна прямым AB и AC. Следовательно, она перпендикулярна плоскости ABC.
Упражнение 21
Слайд 23Докажите, что прямая AB, проходящая через вершины правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
перпендикулярна плоскости BDD1.
Доказательство. Прямая AB перпендикулярна прямым BB1 и BD. Следовательно, она перпендикулярна плоскости BDD1.
Упражнение 22
Слайд 24Докажите, что прямая BD, проходящая через вершины правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
перпендикулярна плоскости ABB1.
Доказательство. Прямая BD перпендикулярна прямым BB1 и AB. Следовательно, она перпендикулярна плоскости ABB1.
Упражнение 23
Слайд 25Докажите, что прямая CF, проходящая через вершины правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
перпендикулярна плоскости BDD1.
Доказательство. Прямая CF параллельна прямой AB, которая перпендикулярна плоскости BDD1. Следовательно, прямая CF также перпендикулярна плоскости BDD1.
Упражнение 24
Слайд 26Докажите, что прямая AC, проходящая через вершины правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
перпендикулярна плоскости BEE1.
Доказательство. Прямая AC перпендикулярна прямым BE и BB1. Следовательно, она перпендикулярна плоскости BEE1.
Упражнение 25
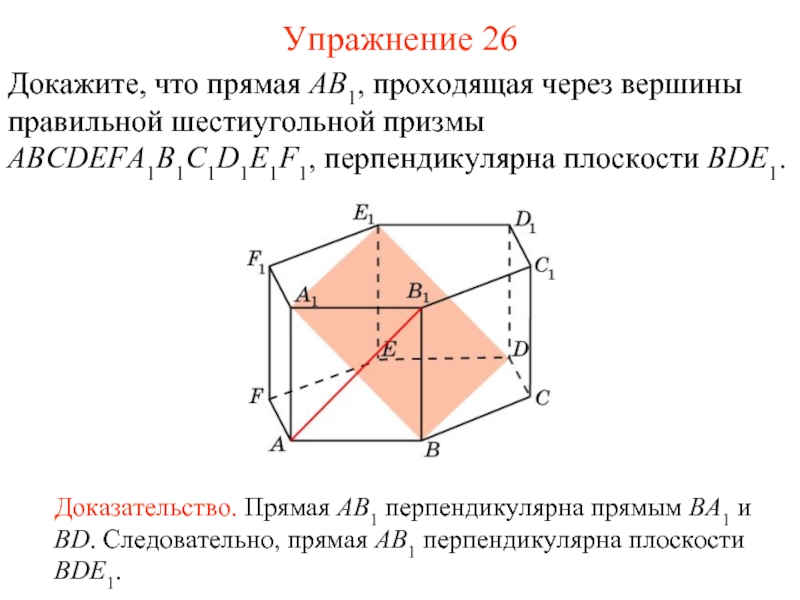
Слайд 27Докажите, что прямая AB1, проходящая через вершины правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1,
перпендикулярна плоскости BDE1.
Доказательство. Прямая AB1 перпендикулярна прямым BA1 и BD. Следовательно, прямая AB1 перпендикулярна плоскости BDE1.
Упражнение 26
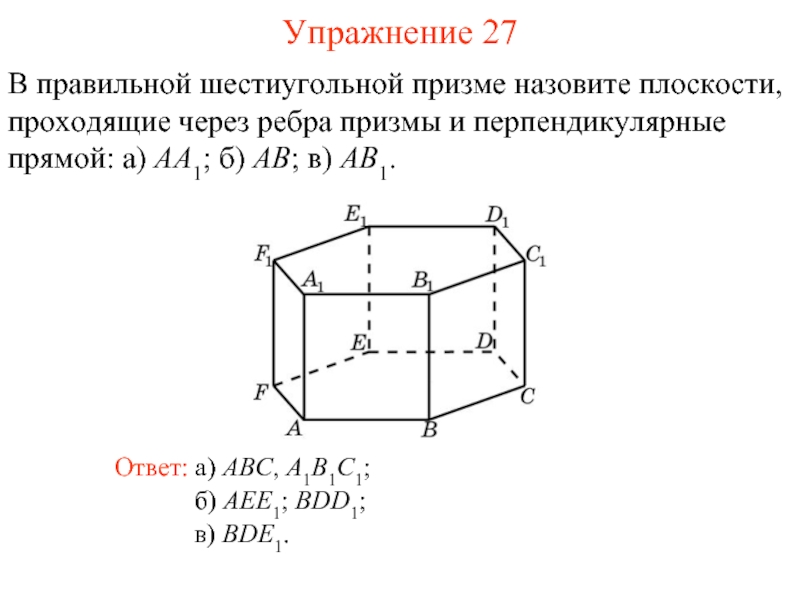
Слайд 28В правильной шестиугольной призме назовите плоскости, проходящие через ребра призмы и
перпендикулярные прямой: а) AA1; б) AB; в) AB1.
б) AEE1; BDD1;
Ответ: а) ABC, A1B1C1;
Упражнение 27
в) BDE1.
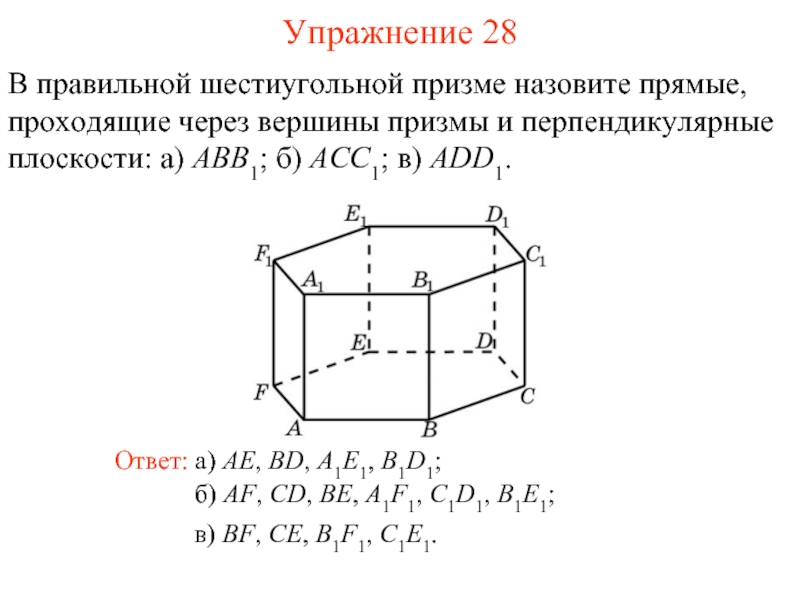
Слайд 29В правильной шестиугольной призме назовите прямые, проходящие через вершины призмы и
перпендикулярные плоскости: а) ABB1; б) ACC1; в) ADD1.
б) AF, CD, BE, A1F1, C1D1, B1E1;
Ответ: а) AE, BD, A1E1, B1D1;
Упражнение 28
в) BF, CE, B1F1, C1E1.
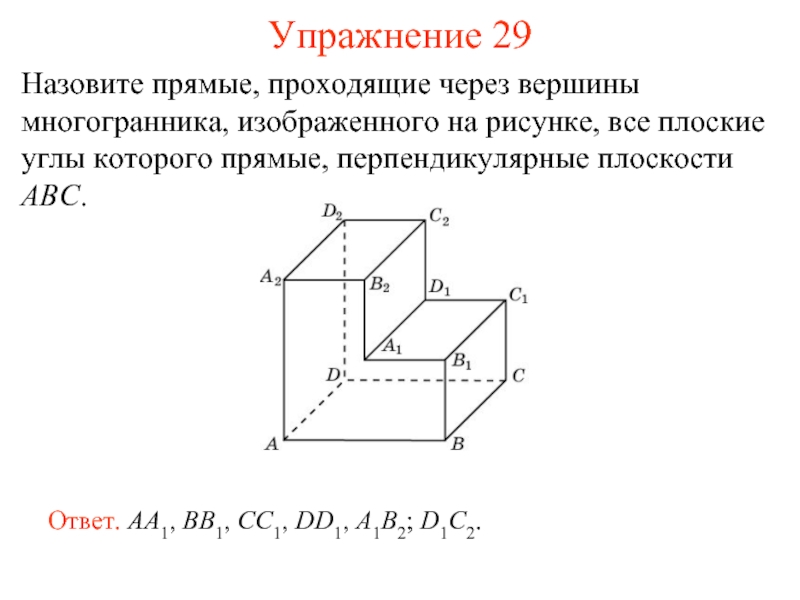
Слайд 30Назовите прямые, проходящие через вершины многогранника, изображенного на рисунке, все плоские
углы которого прямые, перпендикулярные плоскости ABC.
Ответ. AA1, BB1, CC1, DD1, A1B2; D1C2.
Упражнение 29
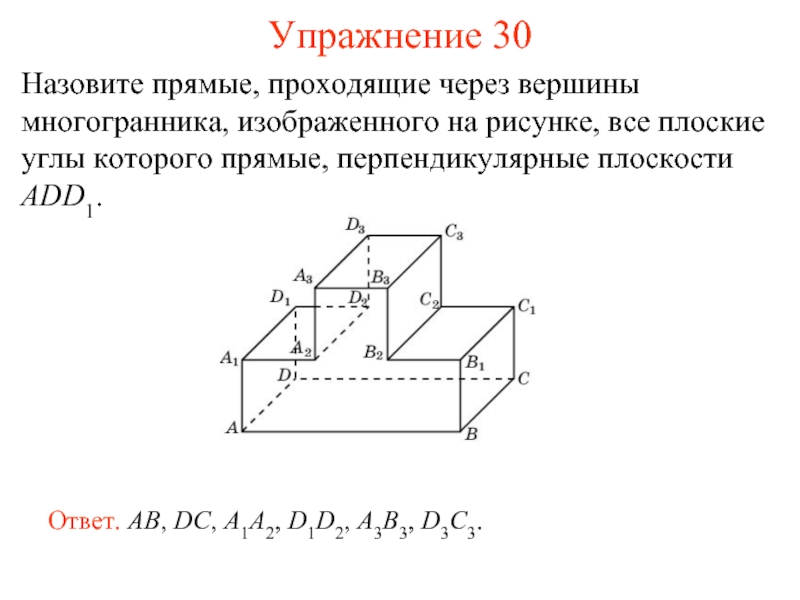
Слайд 31Назовите прямые, проходящие через вершины многогранника, изображенного на рисунке, все плоские
углы которого прямые, перпендикулярные плоскости ADD1.
Ответ. AB, DC, A1A2, D1D2, A3B3, D3C3.
Упражнение 30
