- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы практической био-медицинской статистики. t-критерий Стьюдента. Условия применимости. Интерпретация результатов презентация
Содержание
- 1. Основы практической био-медицинской статистики. t-критерий Стьюдента. Условия применимости. Интерпретация результатов
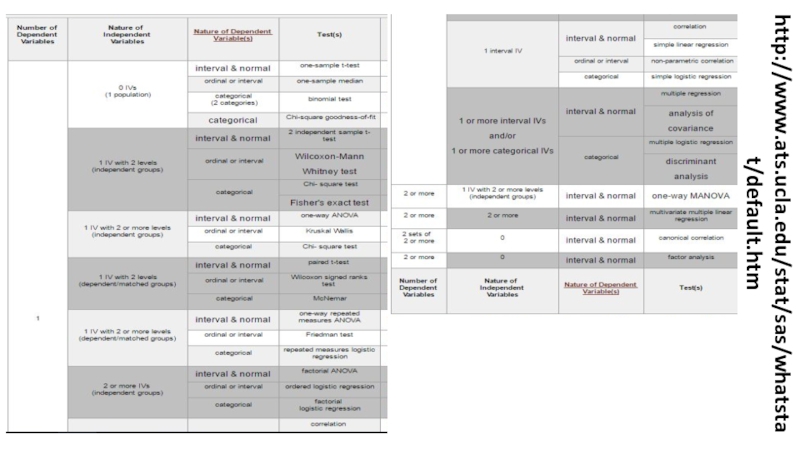
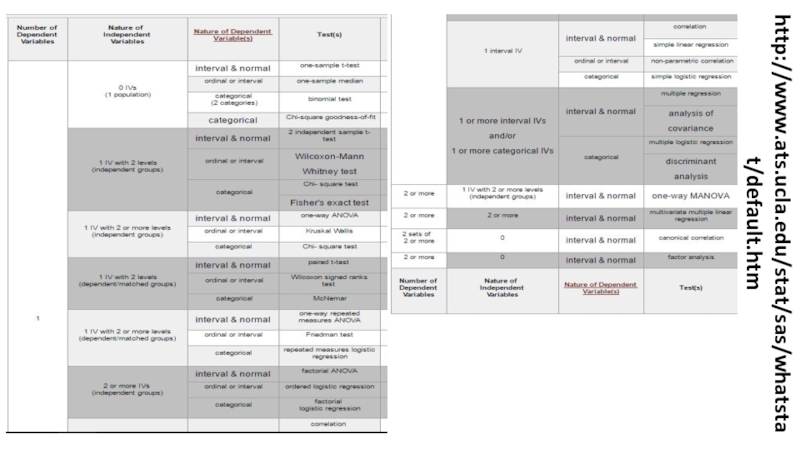
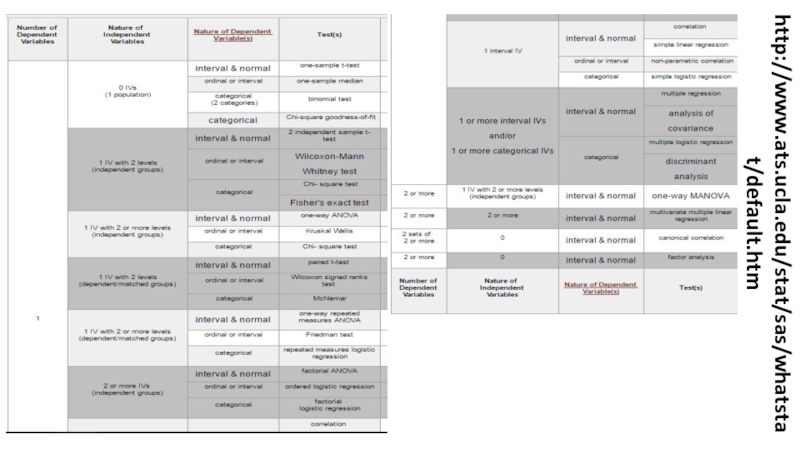
- 2. http://www.ats.ucla.edu/stat/sas/whatstat/default.htm
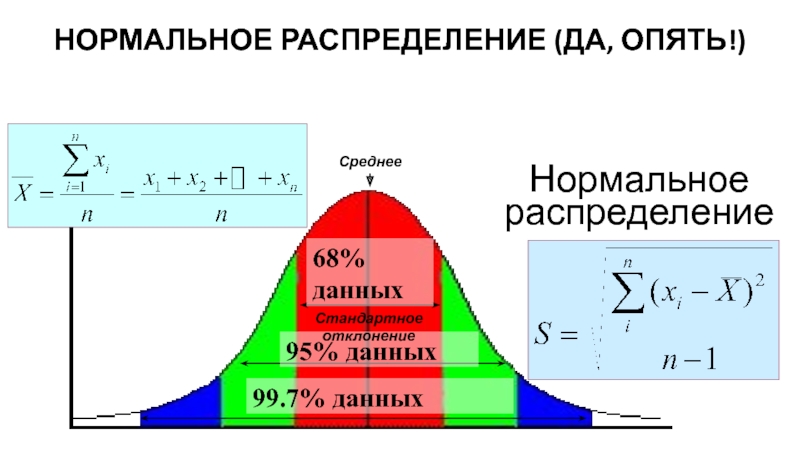
- 3. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (ДА, ОПЯТЬ!) Нормальное распределение Среднее Стандартное отклонение
- 4. Стандартизованное Z-значение Ответ на вопрос «как далеко
- 6. Тестирование гипотез - пример
- 7. Тестирование статистических гипотез (прод.) Случайная простая выборка
- 8. Тестирование статистических гипотез (прод.)
- 9. Тестирование статистических гипотез (прод.) Решение (прод.): Статистика
- 10. Тестирование статистических гипотез (прод.)
- 11. Доверительный интервал для среднего Когда мы приводим
- 12. http://www.ats.ucla.edu/stat/sas/whatstat/default.htm
- 13. t-критерий Стьюдента: анализ одной зависимой количественной переменной
- 14. t-критерий Стьюдента для несвязанных совокупностей: Исследовалась длительность
- 15. t-критерий Стьюдента: Пример приведен из: С.Гланц. Медико-биологическая статистика. – М.Практика, 1998
- 16. Статистика t-критерия:
- 18. Предположения (ограничения) для t-теста для независимых совокупностей
- 19. http://www.ats.ucla.edu/stat/sas/whatstat/default.htm
- 20. Анализ для связанных совокупностей: Анализ показателя у
- 21. Предположения (ограничения) для парного t-теста: Пары должны
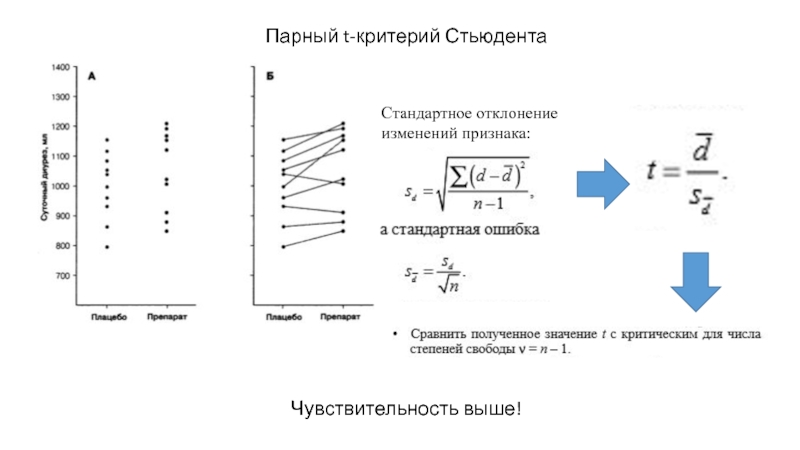
- 22. Парный t-критерий Стьюдента Стандартное отклонение изменений признака: Чувствительность выше!
- 24. Дисперсионный анализ (one-way ANOVA):
- 25. Дисперсионный анализ (one-way ANOVA): Исследовалась длительность госпитализации
- 26. Дисперсионный анализ (one-way ANOVA): Пример приведен из: С.Гланц. Медико-биологическая статистика. – М.Практика, 1998
- 27. Дисперсионный анализ – анализ выборок по разности
- 28. P
- 29. Длительность госпитализации: итоги Леченные правильно находились в
- 30. Требования для дисперсионного анализа: Наблюдения независимо отобраны
Слайд 1ОСНОВЫ ПРАКТИЧЕСКОЙ БИО-МЕДИЦИНСКОЙ СТАТИСТИКИ
СЕРИЯ 3
t-критерий Стьюдента. Условия применимости. Интерпретация результатов. Примеры
Множественные сравнения. Поправка Бонферрони. Дисперсионный анализ. Примеры использования.
Попарные сравнения по результатам дисперсионного анализа. Примеры использования. Трактовка результатов.
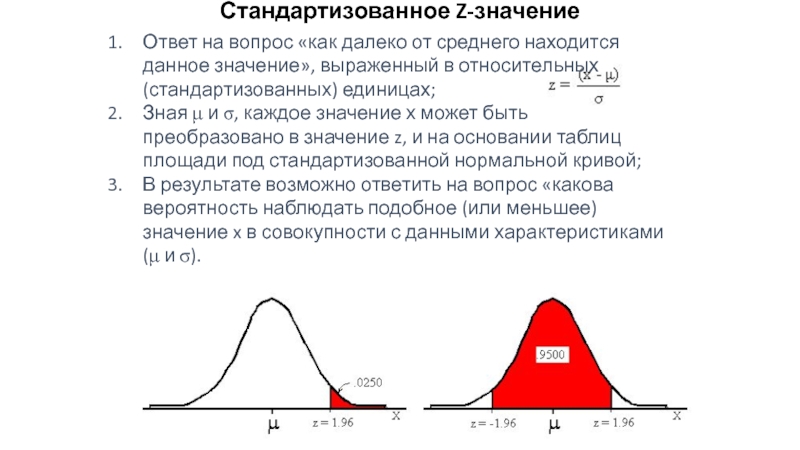
Слайд 4Стандартизованное Z-значение
Ответ на вопрос «как далеко от среднего находится данное значение»,
Зная μ и σ, каждое значение х может быть преобразовано в значение z, и на основании таблиц площади под стандартизованной нормальной кривой;
В результате возможно ответить на вопрос «какова вероятность наблюдать подобное (или меньшее) значение x в совокупности с данными характеристиками (μ и σ).
Слайд 7Тестирование статистических гипотез (прод.)
Случайная простая выборка из 10 человек сделана из
Слайд 9Тестирование статистических гипотез (прод.)
Решение (прод.):
Статистика теста:
Распределение статистики теста: если предположения
Критерии принятия решения:
Отвергнуть H0, если рассчитанное z попадает в область неприятия гипотезы
Невозможность отвергнуть H0, если рассчитанное z попадает в область приятия гипотезы
Слайд 10Тестирование статистических гипотез (прод.)
В силу структуры H0 данный тест относится к
Результат: H0 отвергнута для уровня значимости α=0.05. Заключение: μ≠30, р=0.034
Слайд 11Доверительный интервал для среднего
Когда мы приводим 1-α процентный доверительный интервал для
Т.е. если мы возьмем из совокупности ВСЕ выборки и для каждой рассчитаем доверительный интервал, то истинное среднее будет содержаться в 1-α интервалов.
СТАТИСТИЧЕСКИЙ ТЕСТ НАОБОРОТ!
Слайд 13t-критерий Стьюдента:
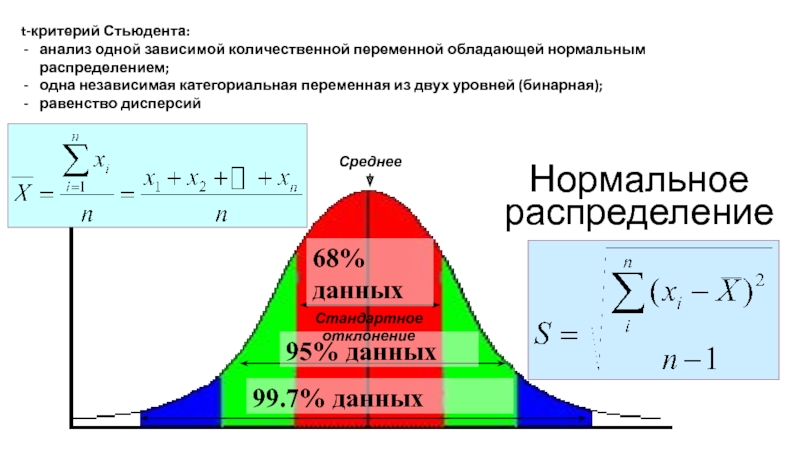
анализ одной зависимой количественной переменной обладающей нормальным распределением;
одна независимая категориальная
равенство дисперсий
Нормальное распределение
Среднее
Стандартное отклонение
Слайд 14t-критерий Стьюдента для несвязанных совокупностей:
Исследовалась длительность госпитализации пациентов с острым пиелонефритом
Средняя длительность госпитализации составила:
В группе леченных «правильно» 4,51+/-1,98 сут.
В группе леченных «неправильно» 6,28+/-2,54 сут.
Можно ли считать эти различия случайными?
Слайд 15t-критерий Стьюдента:
Пример приведен из: С.Гланц. Медико-биологическая статистика. – М.Практика, 1998
Слайд 18Предположения (ограничения) для t-теста для независимых совокупностей
Выборки сделаны случайным образом (или,
Выборки не связаны между собой (если субъекты попарно подобраны, или это измерения по типу «до-после», должен быть использован парный критерий
Наблюдения внутри каждой выборки были получены независимо друг от друга (выбор одного не изменяет вероятность попасть в группу для других)
Данные получены из выборки с (приблизительно) нормальным распределением. Для больших выборок это не столь важное требование
SD двух популяций должна быть равны (иначе использовать модифицированный t-тест)
Гомоскедастичность
Слайд 20Анализ для связанных совокупностей:
Анализ показателя у каждого пациента до и после
Набор пациентов попарно, с учетом таких показателей, как возраст, диагноз, пол и т.п.
Измерение показателя у близнецов или у пар родитель/ребенок
В целом – при любой ситуации, когда есть основания думать, что значение показателя конкретного субъекта из группы А «ближе» к значениям показателя другого (а не случайно выбранного) субъекта из группы В
Слайд 21Предположения (ограничения) для парного t-теста:
Пары должны быть случайным образом отобраны из
Наблюдения должны быть попарно сгруппированы, это делается при планировании эксперимента, и нельзя делать после получения данных
Каждая пара должна быть отобрана независимо от других пар
Распределение разности между парными значениями в популяции должно аппроксимироваться нормальным распределением
Слайд 25Дисперсионный анализ (one-way ANOVA):
Исследовалась длительность госпитализации пациентов с острым пиелонефритом в
Средняя длительность госпитализации составила:
В группе леченных «правильно» 4,51+/-1,98 сут.
В группе леченных «неправильно» 6,28+/-2,54 сут.
Можно ли считать эти различия случайными?
Слайд 26Дисперсионный анализ (one-way ANOVA):
Пример приведен из: С.Гланц. Медико-биологическая статистика. – М.Практика,
Слайд 27Дисперсионный анализ – анализ выборок по разности дисперсий для n уровней
S2вну= (S21+ S22+…+ S2n)/n
νмеж = m – 1
νвну = m (n – 1),
где m – число групп,
n – число случаев
в каждой группе
(меньшее)
Далее – попарные сравнения!
Слайд 29Длительность госпитализации: итоги
Леченные правильно находились в больнице меньше чем, леченные неправильно
Значит ли это, что благодаря правильному лечению больные выздоравливают быстрее?
Увы, нет. Как это всегда бывает в обсервационном исследовании, мы не можем исключить того, что группы различались чем-то еще кроме лечения. Может быть, врачи, которые лечат «по справочнику» просто более склонны быстрее выписывать своих больных?
Слайд 30Требования для дисперсионного анализа:
Наблюдения независимо отобраны из большей популяции или (как
Выборки получены независимо (если субъекты отобраны попарно, или наблюдения носят характер «до-после», необходимо использовать ANOVA с повторными измерениями
Наблюдения внутри каждой выборки получены независимо друг от друга, связи между наблюдениями в группе должны быть равны (2 пациента измеренные 2 раза ≠ 4 измерениям)
Данные получены из выборки с распределением показателя, близким к нормальному, SD для всех популяций должны быть идентичны