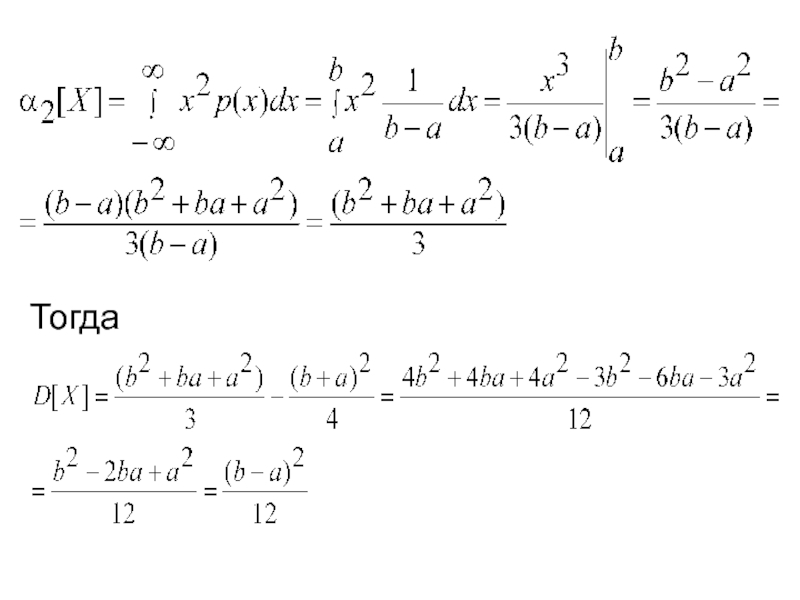§3.6.1.1.Биномиальное распределение
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные законы распределения случайных величин. Законы распределения дискретных случайных величин презентация
Содержание
- 1. Основные законы распределения случайных величин. Законы распределения дискретных случайных величин
- 2. Дискретная СВ Х, принимающая неотрицательные целочисленные значения,
- 3. Вероятность появления события А равна р, а
- 4. Для вычисления числовых характеристик этого распределения нам
- 5. Определим числовые характеристики БЗР. Принимая во
- 6. С учетом второго вспомогательного равенства определим дисперсию:
- 7. Пример: Устройство состоит из трех независимо работающих
- 8. Р3,0 = q3 = 0,93 = 0,729;
- 9. §3.6.1.2. Распределение Пуассона Теорема Пуассона. Если р→0
- 10. Для доказательства теоремы воспользуемся формулой Бернулли. Т.к.
- 11. Использовались соотношения:
- 12. Т.о., дискретная СВ, принимающая целые неотрицательные значения
- 13. Ряд распределения этой СВ имеет вид:
- 14. Числовые характеристики этого
- 15. Принимая во внимание, что D[X]=α2[X] –
- 16. Т.о., D[X]=α2[X] – (M[X])2 =λ(λ+1)- λ2=λ. Величина
- 17. Пример: Учебник издан тиражом 100000 экземпляров. Вероятность
- 18. §3.6.2.Основные законы распределения непрерывных случайных величин §3.6.2.1. Равномерное распределение
- 19. Непрерывная СВ называется равномерно распределенной на интервале
- 20. Т.е. Отсюда С=1/(b-a).
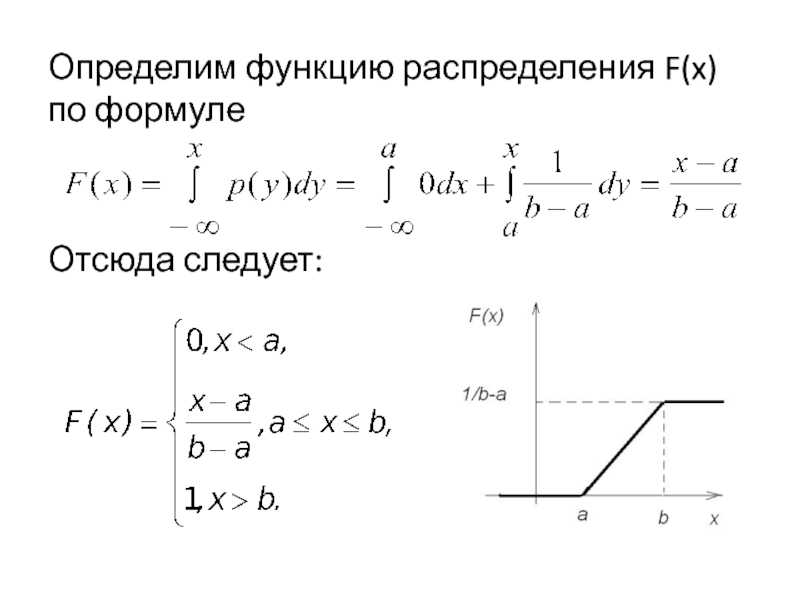
- 21. Определим функцию распределения F(x) по формуле Отсюда следует:
- 22. Определим числовые характеристики распределения M[X], D[X]:
- 23. Тогда
- 24. Стандартное отклонение определяется по формуле:
- 25. Пример: Цена деления шкалы амперметра равна 0,1А.
- 26. В рассматриваемой задаче длина интервала, в котором
Слайд 1§3.6. Основные законы распределения случайных величин §3.6.1.Законы распределения дискретных случайных величин
Слайд 2Дискретная СВ Х, принимающая неотрицательные целочисленные значения, - 0,1,2,…, n называется
распределенной по биномиальному закону, если она принимает указанное значение m с вероятностью
Pm,n=P(X=m)=
По схеме Бернулли СВ Х есть число появлений события А ровно m раз в серии n опытов.
Pm,n=P(X=m)=
По схеме Бернулли СВ Х есть число появлений события А ровно m раз в серии n опытов.
Слайд 3Вероятность появления события А равна р, а непоявления q=(1-p).
ФР F(x) биномиального
закона распределения (БЗР) СВ Х имеет вид
Слайд 4Для вычисления числовых характеристик этого распределения нам потребуется два вспомогательных равенства:
Слайд 5
Определим числовые характеристики БЗР. Принимая во внимание первое вспомогательное равенство определим
МО:
M[X]=mx=
M[X]=mx=
Слайд 6С учетом второго вспомогательного равенства определим дисперсию:
D[X]=α2[X] - mx =
=
Величины n, p называются параметрами распределения.
Слайд 7Пример: Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого
элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение: Х - число отказавших элементов в одном опыте; х1 = 0 (ни один из элементов не отказал); х2 = 1 (отказал один элемент); х3 = 2 (отказали два элемента); х4 = 3 (отказали три элемента); n = 3; р = 0,1, следовательно, q = 1 - 0,1 = 0,9
Решение: Х - число отказавших элементов в одном опыте; х1 = 0 (ни один из элементов не отказал); х2 = 1 (отказал один элемент); х3 = 2 (отказали два элемента); х4 = 3 (отказали три элемента); n = 3; р = 0,1, следовательно, q = 1 - 0,1 = 0,9
Слайд 8Р3,0 = q3 = 0,93 = 0,729;
Р3,1 = С13 р q2
=3 0,1 0,92 = 0,243;
Р3,2 = С23 р2 q = 3 0,12 0,9 = 0,027;
Р3,3 = р3 = 0,13 = 0,001.
Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1.
Искомый биномиальный закон распределения Х:
X 0 1 2 3
p 0,729 0,243 0,027 0,001
Р3,2 = С23 р2 q = 3 0,12 0,9 = 0,027;
Р3,3 = р3 = 0,13 = 0,001.
Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1.
Искомый биномиальный закон распределения Х:
X 0 1 2 3
p 0,729 0,243 0,027 0,001
Слайд 9§3.6.1.2. Распределение Пуассона
Теорема Пуассона. Если р→0 при n→∞, а np=λ, λ=const,
то СВ может принимать целые неотрицательные значения с вероятностями
Слайд 10Для доказательства теоремы воспользуемся формулой Бернулли. Т.к. np=λ, p=λ/n и р→0
при n→∞, то
Слайд 12Т.о., дискретная СВ, принимающая целые неотрицательные значения 0, 1, 2,…, m
с вероятностью
называется распределенной по закону Пуассона.
называется распределенной по закону Пуассона.
Слайд 14
Числовые характеристики этого закона:
M[X]=
и покажем, что дисперсия распределения Пуассона
тоже равна λ.
Слайд 15Принимая во внимание, что
D[X]=α2[X] – (M[X])2, вычислим сначала второй начальный
момент:
α2[X]=
α2[X]=
Слайд 16Т.о., D[X]=α2[X] – (M[X])2 =λ(λ+1)- λ2=λ.
Величина λ называется параметром распределения.
Вид
распределения Пуассона изменяется при различных значениях параметра распределения λ. При малых значениях λ наблюдается асимметрия закона распределения. С ростом λ имеется тенденция к симметрии.
Слайд 17Пример: Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован
неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение: n=100000, p=0,0001, m=5.
Определим λ: λ=np=100000 ⋅ 0,0001=10
Искомая вероятность
P100000(5)=105e-10/5!=0,0378
Решение: n=100000, p=0,0001, m=5.
Определим λ: λ=np=100000 ⋅ 0,0001=10
Искомая вероятность
P100000(5)=105e-10/5!=0,0378
Слайд 18§3.6.2.Основные законы распределения непрерывных случайных величин
§3.6.2.1. Равномерное распределение
Слайд 19Непрерывная СВ называется равномерно распределенной на интервале [a, b], если плотность
ее распределения имеет постоянное значение С.
р(х)=
Определим C=const из условия нормировки
р(х)=
Определим C=const из условия нормировки
Слайд 22Определим числовые характеристики распределения M[X], D[X]:
Отсюда следует, что МО совпадает
с медианой. Определим дисперсию по формуле
D[X]=α2[X]–(M[X])2
D[X]=α2[X]–(M[X])2
Слайд 24Стандартное отклонение определяется по формуле:
Равномерное распределение используется в технических приложениях,
когда информация о характеристиках распределения мала.
Слайд 25Пример: Цена деления шкалы амперметра равна 0,1А. Показания округляют до ближайшего
целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02А.
Решение: Ошибка округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения ƒ(х)=1/(b-a), где (b-a) – длина интервала, в котором заключены возможные значения Х; вне этого интервала ƒ(х)=0.
Решение: Ошибка округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения ƒ(х)=1/(b-a), где (b-a) – длина интервала, в котором заключены возможные значения Х; вне этого интервала ƒ(х)=0.
Слайд 26В рассматриваемой задаче длина интервала, в котором заключены все возможные значения
Х, равна 0,1, т.е. (b-a)=0,1, поэтому ƒ(х)=1/0,1=10.
Из условия задачи ясно, что ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02; 0,08). По формуле
P(a
P(0,02
Из условия задачи ясно, что ошибка отсчета превысит 0,02, если она будет заключена в интервале (0,02; 0,08). По формуле
P(a
P(0,02
