- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основи теорії ймовірності та математичної статистики. (Тема 1) презентация
Содержание
- 1. Основи теорії ймовірності та математичної статистики. (Тема 1)
- 2. Подія– будь-який факт, явище, або процес, що
- 3. Випадкові події ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
- 4. Сумою двох подій A і B називається
- 5. Добутком двох випадкових подій А і В
- 6. Нехай А і В – деякі події,
- 7. Події H1, H2,…, Hn назвемо гіпотезами. Щодо
- 8. Якщо в результаті події відбулася подія А,
- 9. 2. Випадкові величини. Випадкова величина –
- 10. Дискретна випадкова величина – випадкова величина,
- 11. Неперервна випадкова величина – випадкова величина,
- 12. Мішана випадкова величина – випадкова величина,
- 13. Основні числові характеристики випадкових величин та
- 14. а) у випадку, коли всі можливі
- 15. б) якщо випадкова величина х є
- 16. Приклад 1: Надаючи банківський кредит комерційній фірмі,
- 17. Дисперсією випадкової величини X називається математичне сподівання
- 18. а) у випадку, коли х –
- 19. Дисперсія характеризує міру розсіювання (відхилення) випадкової
- 20. Для зручності доцільно використовувати показник середньоквадратичного відхилення
- 21. Приклад 2: Підприємство, розробляючи інвестиційний портфель, вирішує
Слайд 1ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
ТЕМА 1.
ОСНОВИ
ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ
1. Випадкові події
2. Випадкові величини
3. Основні числові характеристики випадкових величин та їх властивості
Слайд 2Подія– будь-який факт, явище, або процес, що розглядаються лише з точки
За своєю природою події поділяють на:
неможливі,
достовірні,
випадкові.
Випадкові події
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 4Сумою двох подій A і B називається подія C, яка полягає
Ймовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій:
P (A+B) = P(A) + P(B).
Сума ймовірностей двох протилежних подій A і дорівнює 1.
Випадкові події
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 5Добутком двох випадкових подій А і В є подія С, що
С=А*В
Ймовірність добутку двох подій дорівнює добутку ймовірностей, якщо ці події незалежні (реалізація однієї не впливає на реалізацію іншої):
Р(А*В)=Р(А)*Р(В)
Випадкові події
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 6Нехай А і В – деякі події, Р(А) та Р(В) –
Умовною ймовірністю події А при умові В (позначається Р(В/А)) називається ймовірність події А, знайдена при умові, що подія В відбулася. Ця ймовірність знаходиться за формулою:
Випадкові події
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 7Події H1, H2,…, Hn назвемо гіпотезами. Щодо гіпотез відомі апріорні ймовірності
Випадкові події
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 8Якщо в результаті події відбулася подія А, то попередні, апріорні ймовірності
Випадкові події
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 92. Випадкові величини.
Випадкова величина – змінна, яка в результаті кожного випробування
Випадкові величини бувають дискретними, неперервними та мішаними.
2. Випадкові величини.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 10
Дискретна випадкова величина – випадкова величина, множина значень якої скінченна або
Прикладом дискретної випадкової величини може бути число викликів, що надходять на телефонну станцію протягом певного проміжку часу, кількість покупців, що прийшли у супермаркет на певний момент часу та ін.
2. Випадкові величини.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 11
Неперервна випадкова величина – випадкова величина, значення якої цілком заповнюють деякий
Прикладом неперервної випадкової величини може бути температура повітря, час безвідмовної роботи обладнання, відсоткова ставка доходу та ін..
2. Випадкові величини.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 12
Мішана випадкова величина – випадкова величина, множина значень якої є об’єднанням
Прикладом мішаної випадкової величини може бути величина виплат страхової фірми, яка набуває значень залежно від суми збитків: якщо величина збитків менша певної наперед визначеної в договорі страхування суми, то величина виплат дорівнюватиме збиткам (неперервна випадкова величина); якщо величина збитків більша страхової суми, то величина виплат дорівнюватиме страховій сумі (дискретна випадкова величина).
2. Випадкові величини.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 13
Основні числові характеристики випадкових величин та їх властивості
Математичним сподіванням дискретної випадкової
Математичне сподівання дискретної випадкової величини Х характеризує середнє значення випадкової величини Х з урахуванням ймовірностей його можливих значень. У практичній діяльності під математичним сподіванням розуміють центр розподілу випадкової величини.
3. Основні числові характеристики випадкових величин.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 14
а) у випадку, коли всі можливі наслідки події описуються дискретною величиною
а розподіл ймовірностей їх настання
причому ,
де n – число можливих наслідків, то математичне сподівання обчислюється:
де хі – значення випадкової величини при і-му можливому наслідку,
рі – ймовірність настання і-го можливого наслідку.
3. Основні числові характеристики випадкових величин.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 15
б) якщо випадкова величина х є неперервною, то формула для математичного
де f(x) – щільність розподілу ймовірностей випадкової величини х.
або
- якщо випадкова величина х визначена на інтервалі [a;b].
3. Основні числові характеристики випадкових величин.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
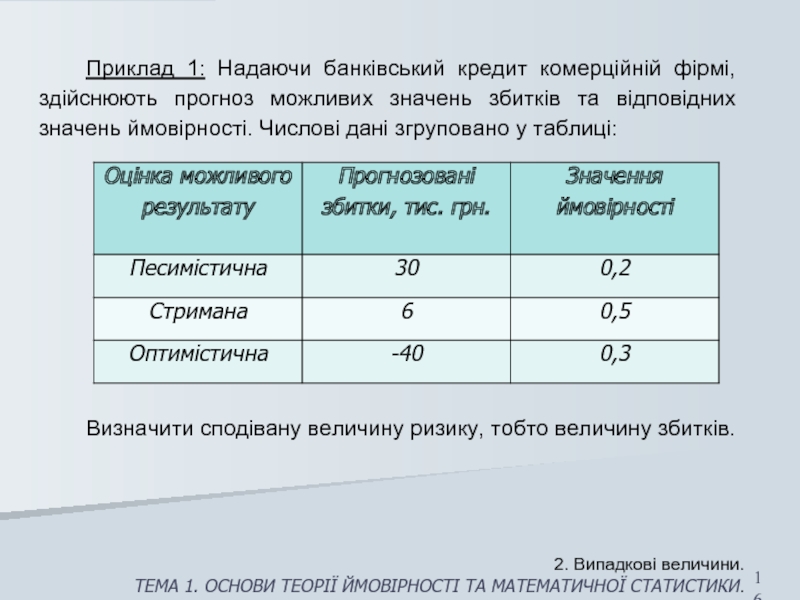
Слайд 16Приклад 1: Надаючи банківський кредит комерційній фірмі, здійснюють прогноз можливих значень
Визначити сподівану величину ризику, тобто величину збитків.
2. Випадкові величини.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 17Дисперсією випадкової величини X називається математичне сподівання квадрата відхилення значень випадкової
Дисперсія характеризує міру розсіювання можливих значень випадкової величини навколо її математичного сподівання.
3. Основні числові характеристики випадкових величин.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 18
а) у випадку, коли х – дискретна випадкова величина:
б)
або
3. Основні числові характеристики випадкових величин.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 19
Дисперсія характеризує міру розсіювання (відхилення) випадкової величини х навколо (від) математичного
Величина дисперсії вимірюється в квадратних одиницях вимірювання випадкової величини.
2. Випадкові величини.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
Слайд 20Для зручності доцільно використовувати показник середньоквадратичного відхилення випадкової величини – це
Середньоквадратичне відхилення вимірюється в одиницях вимірювання випадкової величини.
3. Основні числові характеристики випадкових величин.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.
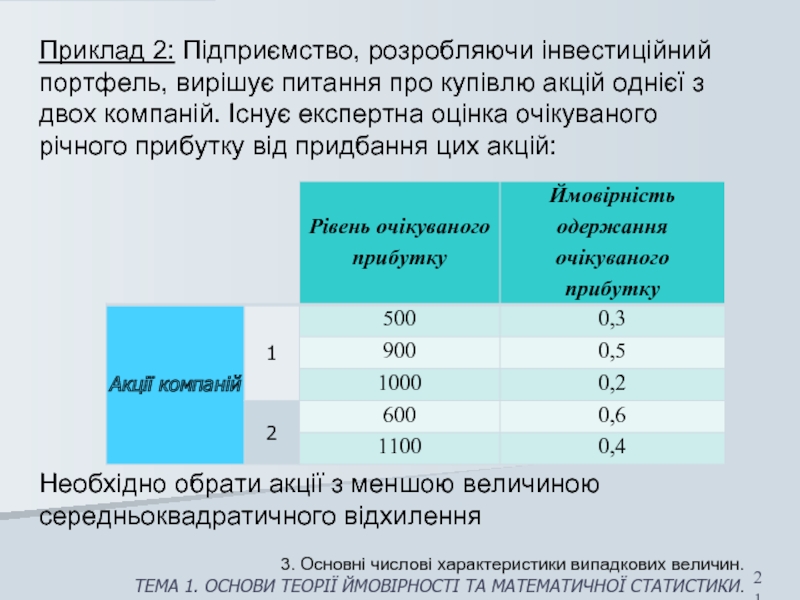
Слайд 21Приклад 2: Підприємство, розробляючи інвестиційний портфель, вирішує питання про купівлю акцій
Необхідно обрати акції з меншою величиною середньоквадратичного відхилення
3. Основні числові характеристики випадкових величин.
ТЕМА 1. ОСНОВИ ТЕОРІЇ ЙМОВІРНОСТІ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ.