- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные свойства функций и их графики презентация
Содержание
- 1. Основные свойства функций и их графики
- 2. Функция. Область определения. Область значений Пусть X
- 3. Если элементами множеств Х и У являются
- 4. Область определения функции f(х) (D(f(х)) – множество
- 5. Пример 1) Область определения
- 6. График функции Графиком функции
- 7. Способы задания функций одной переменной Задать функцию
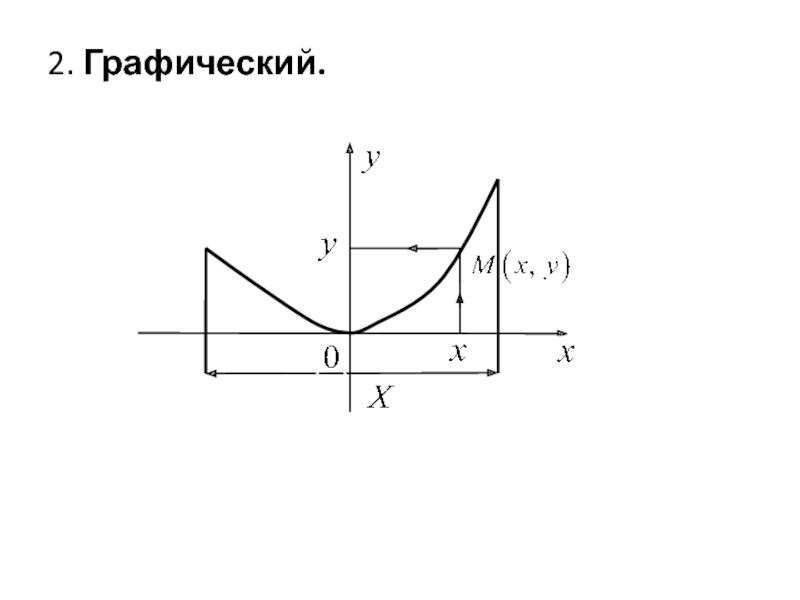
- 8. 2. Графический.
- 9. аналитический, который имеет три разновидности: А) явный
- 10. Свойства функций
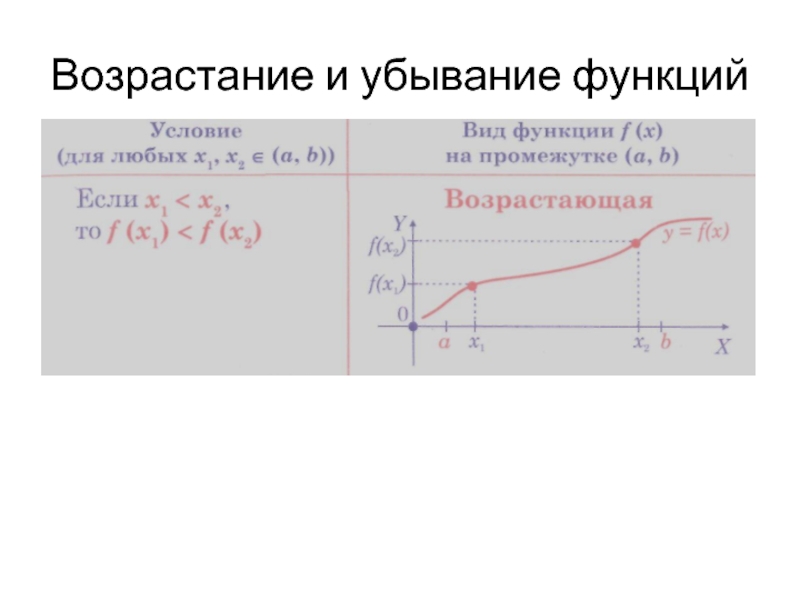
- 11. Возрастание и убывание функций
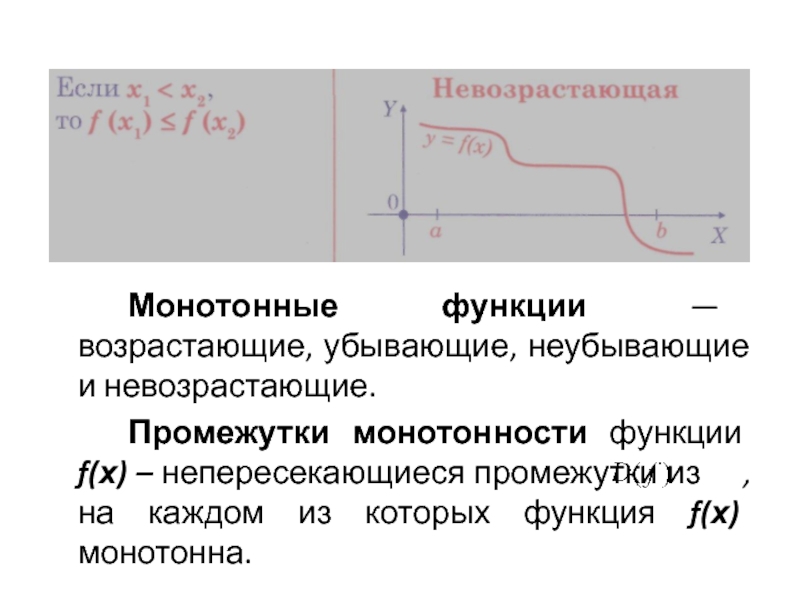
- 13. Монотонные функции — возрастающие, убывающие, неубывающие и
- 14. Четность и нечетность функции
- 15. Пример 1)
- 16. Периодичность функций Функция f(х) периодическая — существует
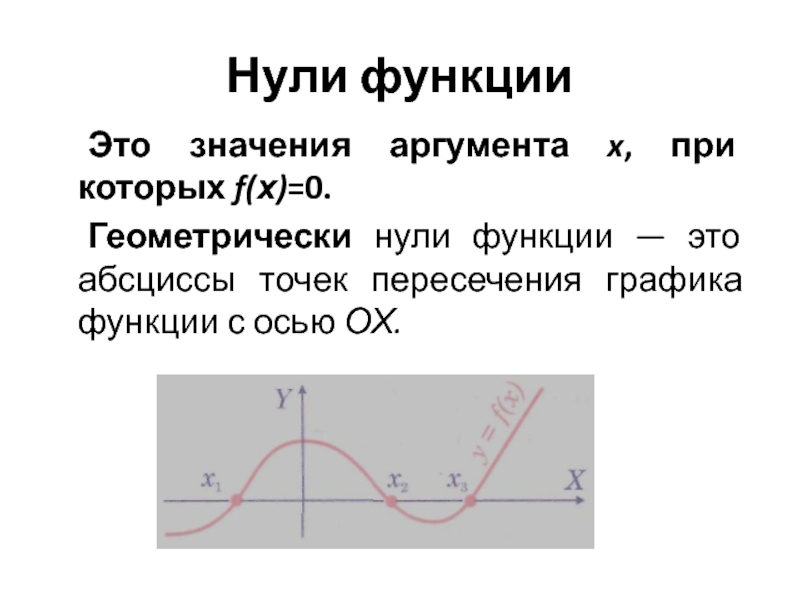
- 17. Нули функции Это значения аргумента x,
- 18. Промежутки знакопостоянства Промежутки знакопостоянства f(х) –промежутки
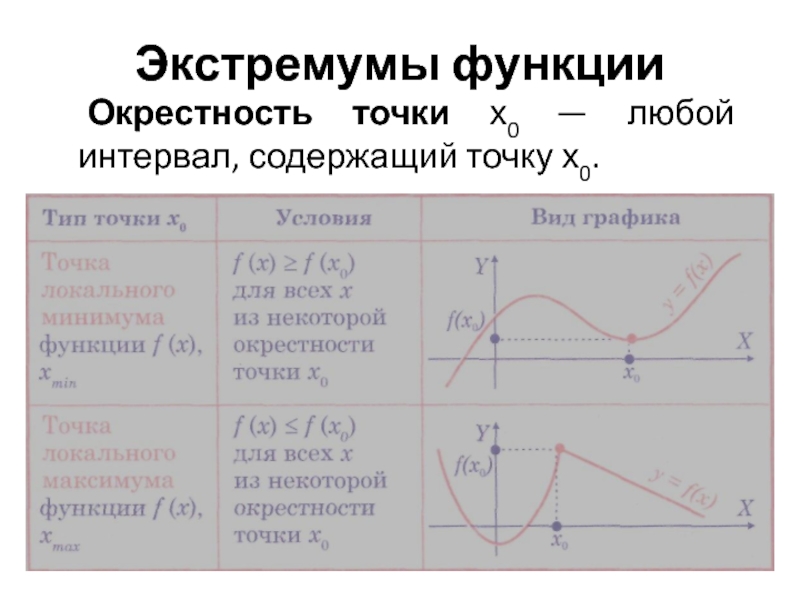
- 19. Экстремумы функции Окрестность точки х0 — любой интервал, содержащий точку х0.
- 20. Точки экстремума — точки минимума и максимума.
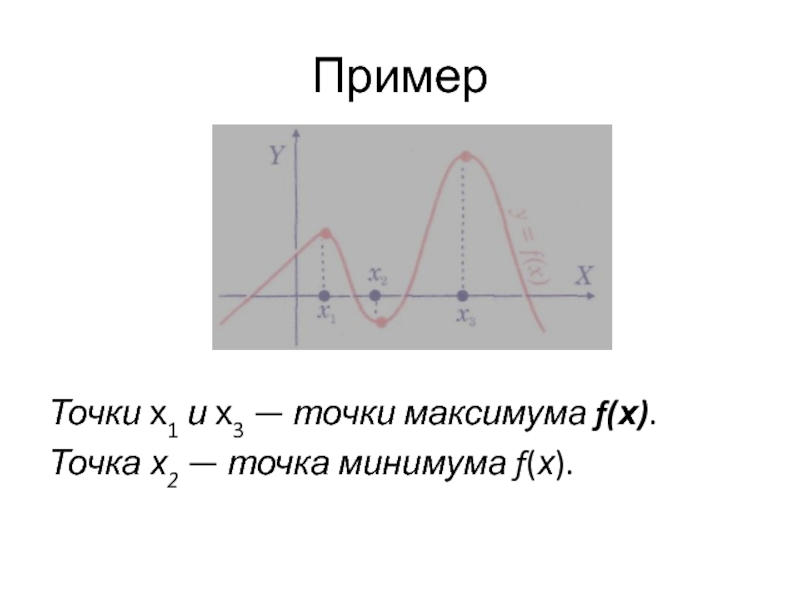
- 21. Пример Точки х1 и х3 — точки
- 22. Свойства функций одной переменной Четность и нечетность
- 23. Основные элементарные функции : 1) Степенная функция
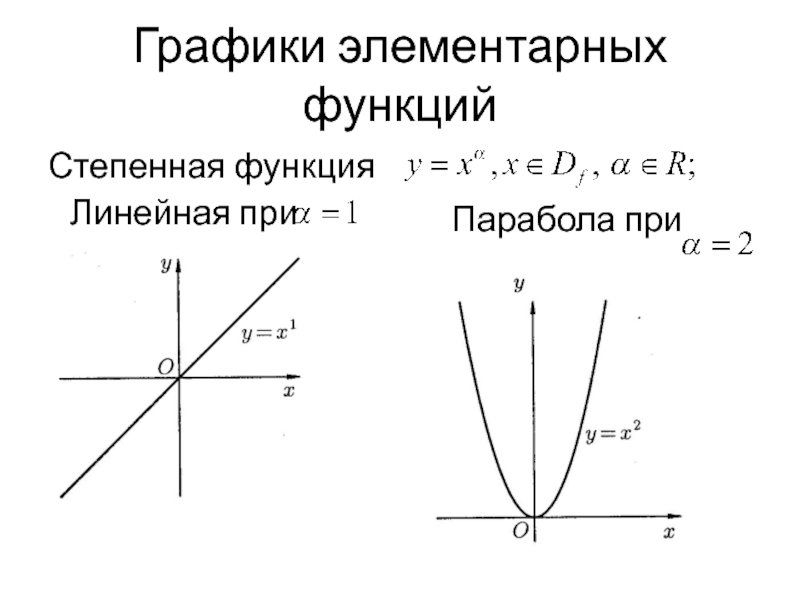
- 24. Графики элементарных функций Степенная функция Линейная при Парабола при
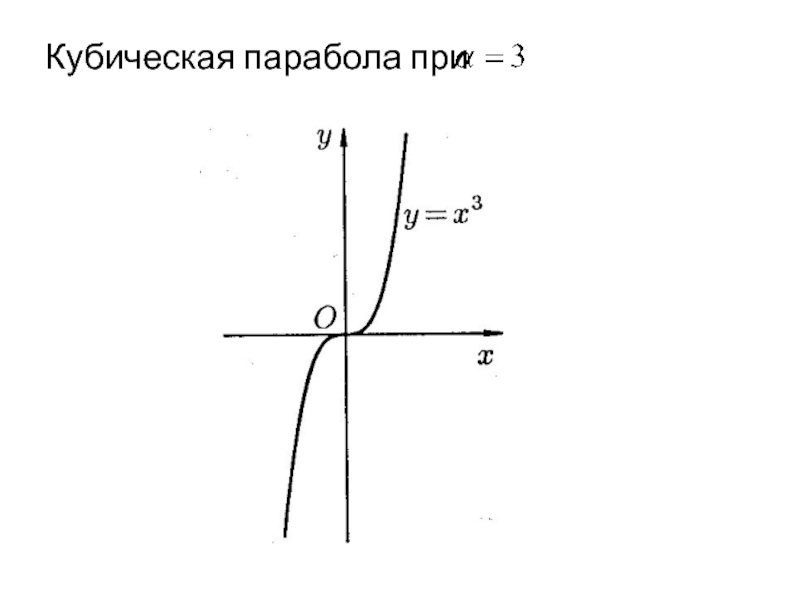
- 25. Кубическая парабола при
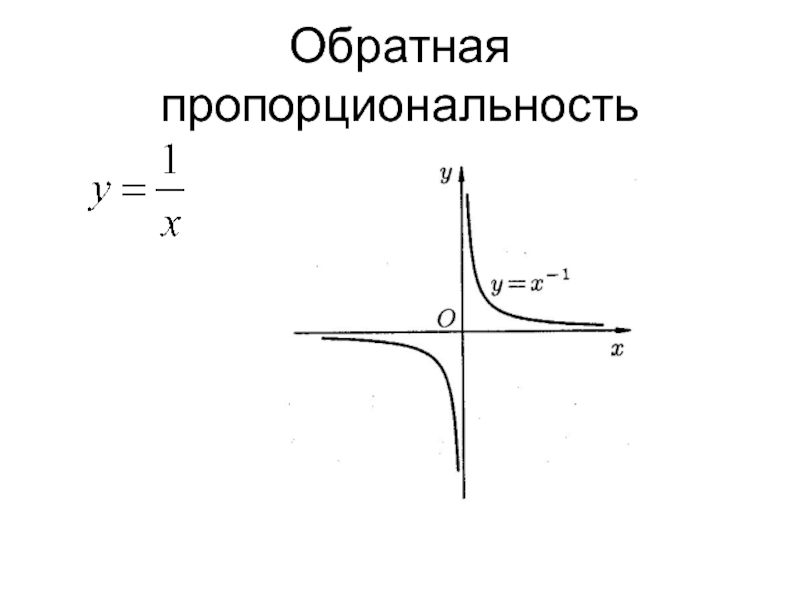
- 26. Обратная пропорциональность
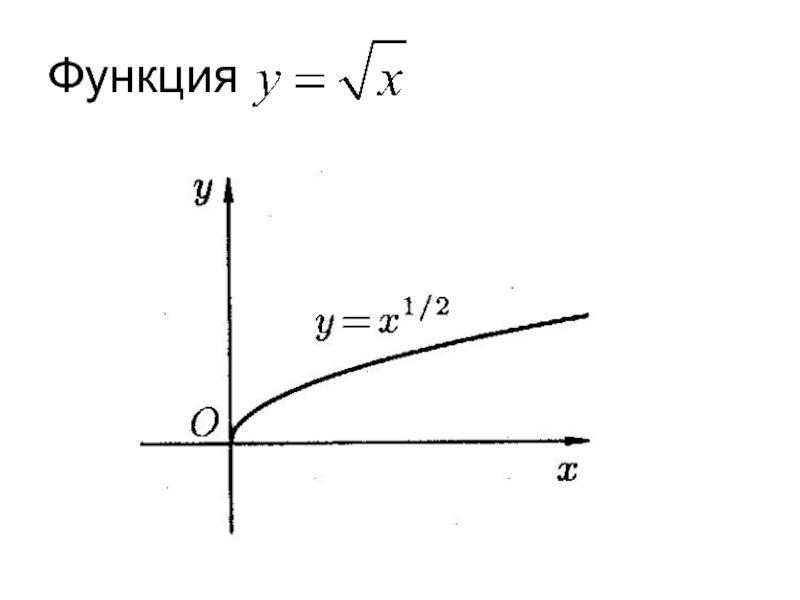
- 27. Функция
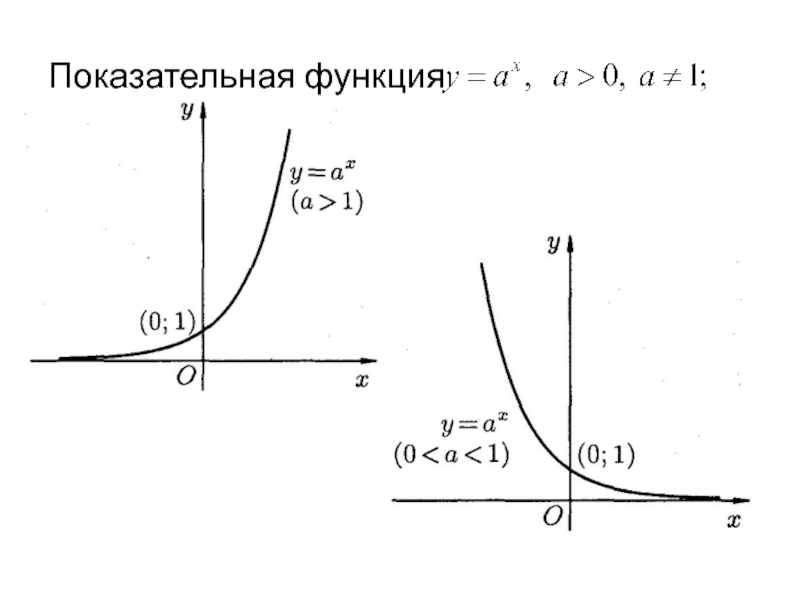
- 28. Показательная функция
- 29. Показательная функция у = ех Показательная функция
- 30. График у = ех
- 31. Логарифмическая функция
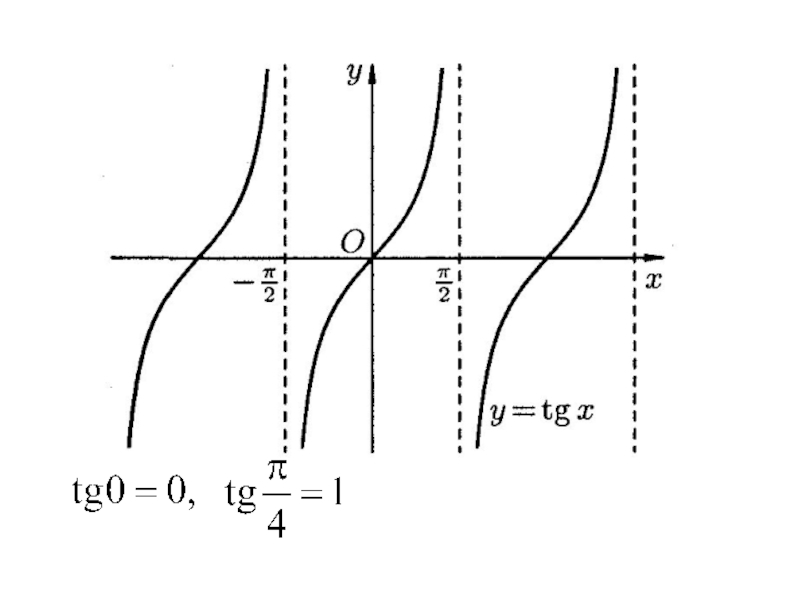
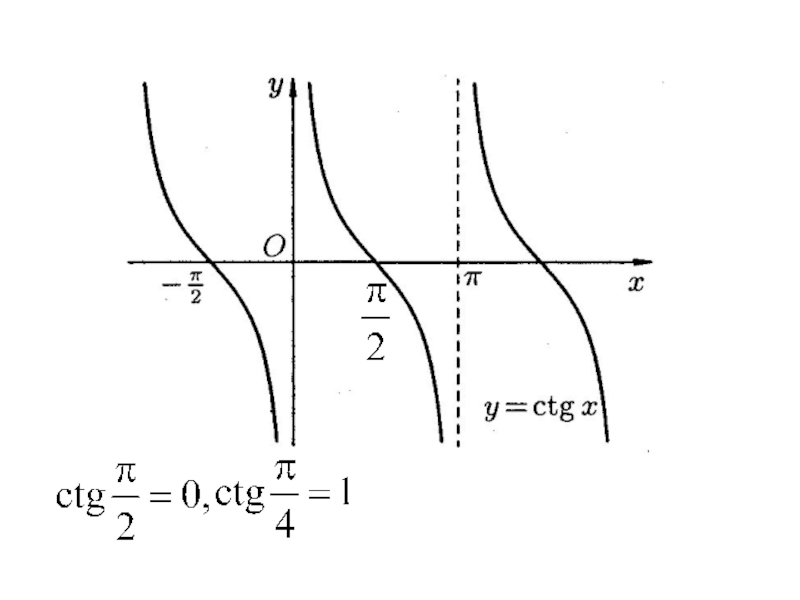
- 32. Тригонометрические функции
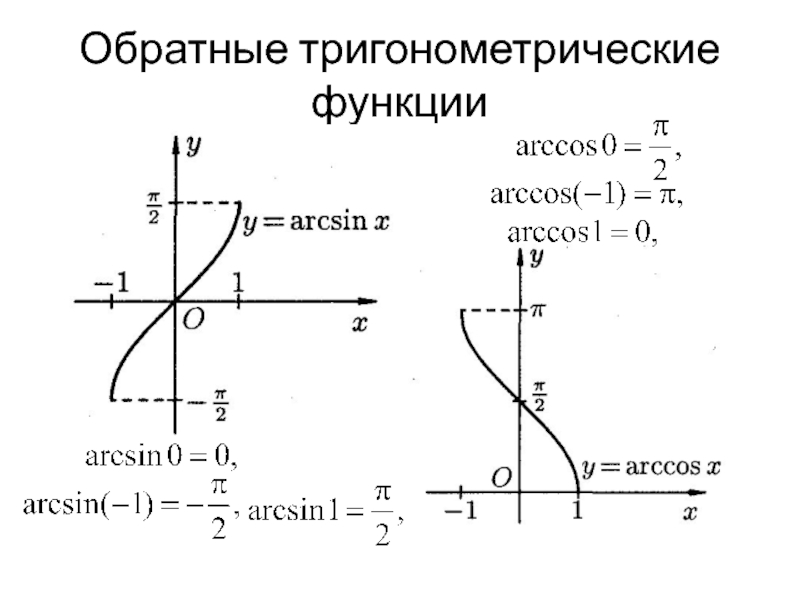
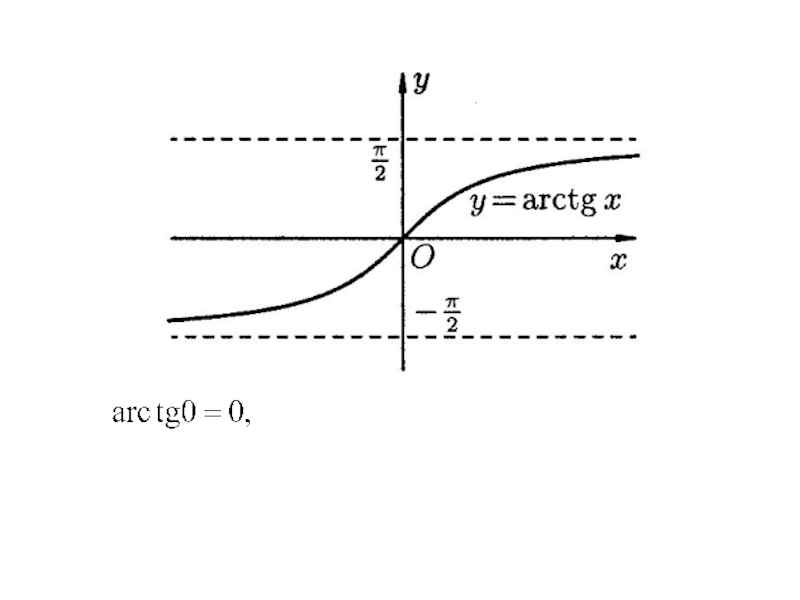
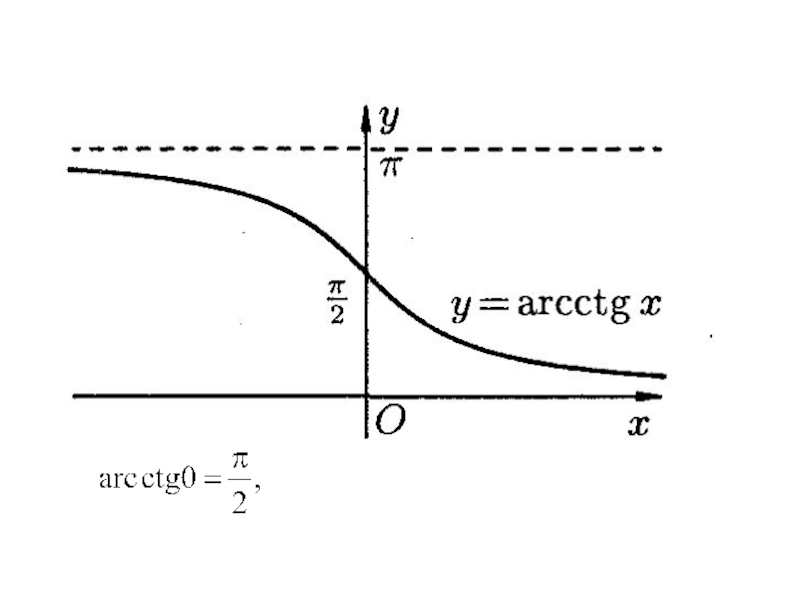
- 36. Обратные тригонометрические функции
- 39. Элементарными функциями называются все функции, которые можно
- 40. Некоторые элементарные функции: 1) линейная функция
- 41. 5) иррациональные функции ‑ функции в которых
- 42. Квадратичная функция Квадратичной функцией называется функция вида
- 43. График квадратичной функции Любую квадратичную функцию
- 44. График функции
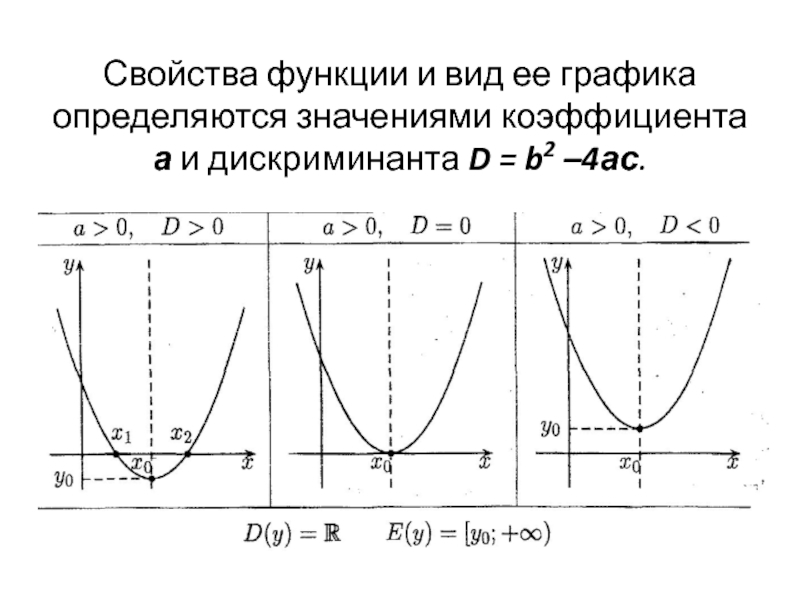
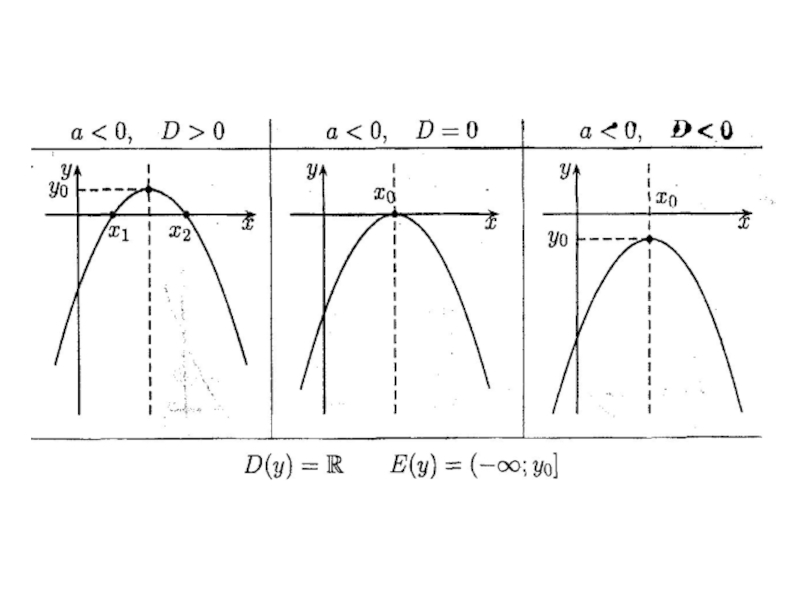
- 45. Свойства функции и вид ее графика определяются
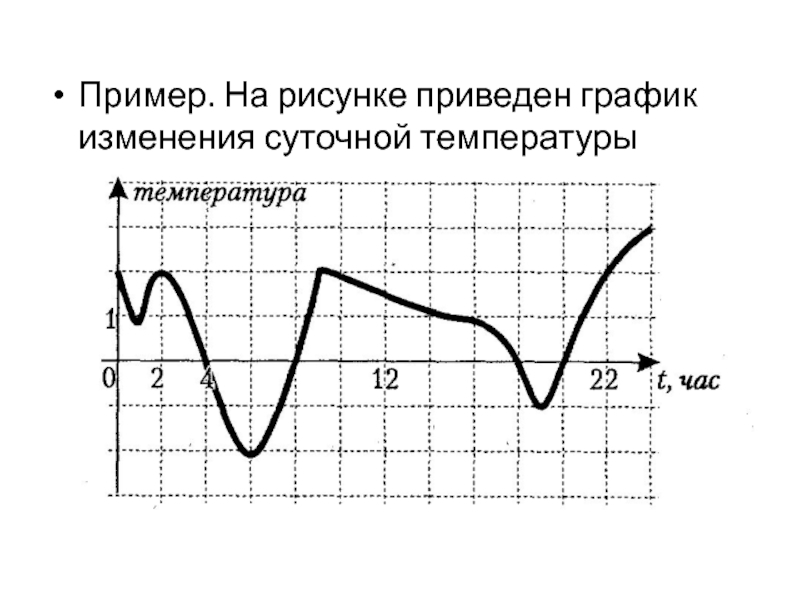
- 47. Пример. На рисунке приведен график изменения суточной температуры
- 48. Определите: a) максимальное и минимальное значение температуры;
Функция. Область определения. Область значений Пусть X и Y— два множества. Функция у=f(х) — это правило или закон f, по которому каждому числу
Слайд 2Функция. Область определения. Область значений
Пусть X и Y— два множества.
Функция у=f(х)
— это правило или закон f, по которому каждому числу
ставится в соответствие единственное число .
ставится в соответствие единственное число .
Слайд 3 Если элементами множеств Х и У являются действительные числа, т. е.
то функцию называют числовой функцией.
Переменная x называется при этом аргументом или независимой пере-менной, а y – функцией или зависимой переменной. Относительно величин x и y говорят, что они находятся в функциональной зависимости.
– частное значение функции при
Переменная x называется при этом аргументом или независимой пере-менной, а y – функцией или зависимой переменной. Относительно величин x и y говорят, что они находятся в функциональной зависимости.
– частное значение функции при
Слайд 4 Область определения функции f(х) (D(f(х)) – множество X, т.е. всевозможные значения
независимой переменной х.
Область значений функции f(х) (E(f(х)) – множество, состоящее из всевозможных чисел f(х) при .
Слайд 6График функции
Графиком функции
является множество
всех точек
плоскости , для каждой из которых значение аргумента x является абсциссой, а значение функции y ‑ ординатой.
плоскости , для каждой из которых значение аргумента x является абсциссой, а значение функции y ‑ ординатой.
Слайд 7Способы задания функций одной переменной
Задать функцию ‑ это значит указать множество
ее определения и правило, при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции.
Три основных способа задания функции:
1. Табличный.
Три основных способа задания функции:
1. Табличный.
Слайд 9аналитический, который имеет три разновидности:
А) явный способ задания ‑ с помощью
одного или нескольких аналитических выра-жений . Например,
Б) неявный, т.е. с помощью уравнения
В) параметрический.
Б) неявный, т.е. с помощью уравнения
В) параметрический.
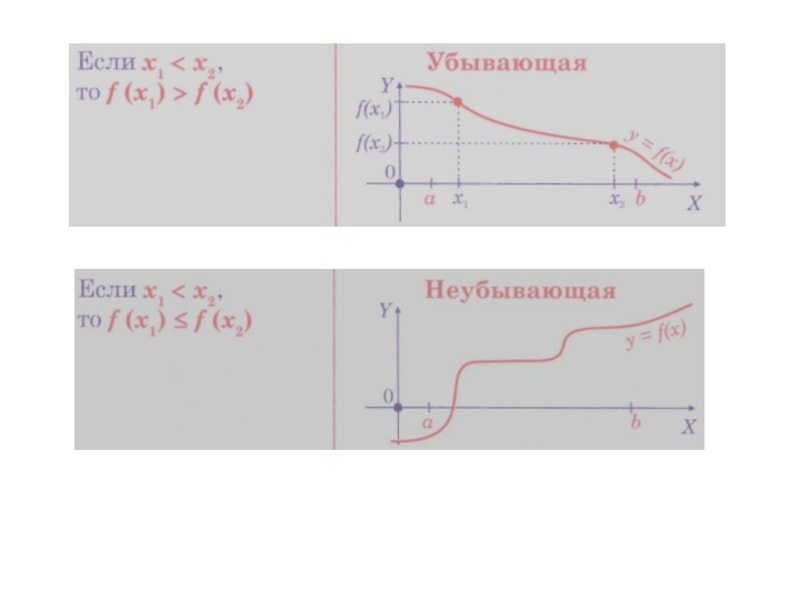
Слайд 13 Монотонные функции — возрастающие, убывающие, неубывающие и невозрастающие.
Промежутки монотонности функции f(х)
– непересекающиеся промежутки из , на каждом из которых функция f(х) монотонна.
Слайд 16Периодичность функций
Функция f(х) периодическая — существует такое число
(период), что:
1) Если , то ;
2) .
Если Т – период f(х), то любое число – тоже период f(х). Основной период — наименьший из положительных периодов.
1) Если , то ;
2) .
Если Т – период f(х), то любое число – тоже период f(х). Основной период — наименьший из положительных периодов.
Слайд 17Нули функции
Это значения аргумента x, при которых f(х)=0.
Геометрически нули функции
— это абсциссы точек пересечения графика функции с осью ОХ.
Слайд 18Промежутки знакопостоянства
Промежутки знакопостоянства f(х) –промежутки из
, на которых либо , либо .
Нули функции f(х) разбивают на промежутки знакопостоянства.
Нули функции f(х) разбивают на промежутки знакопостоянства.
Слайд 20 Точки экстремума — точки минимума и максимума.
Минимум f(х) — значение
f(xmin).
Максимум f(х) — значение f(хтах).
Экстремумы f(х) — минимум и максимум f(х).
Точки экстремума f(х) разбивают D(f) на промежутки монотонности f(x), т.е. промежутки возрастания или убывания функции.
Максимум f(х) — значение f(хтах).
Экстремумы f(х) — минимум и максимум f(х).
Точки экстремума f(х) разбивают D(f) на промежутки монотонности f(x), т.е. промежутки возрастания или убывания функции.
Слайд 22Свойства функций одной переменной
Четность и нечетность функции.
2. Периодичность функции.
3. Монотонность
функции.
4. Ограниченность функции.
4. Ограниченность функции.
Слайд 23Основные элементарные функции :
1) Степенная функция
2) Показательная функция
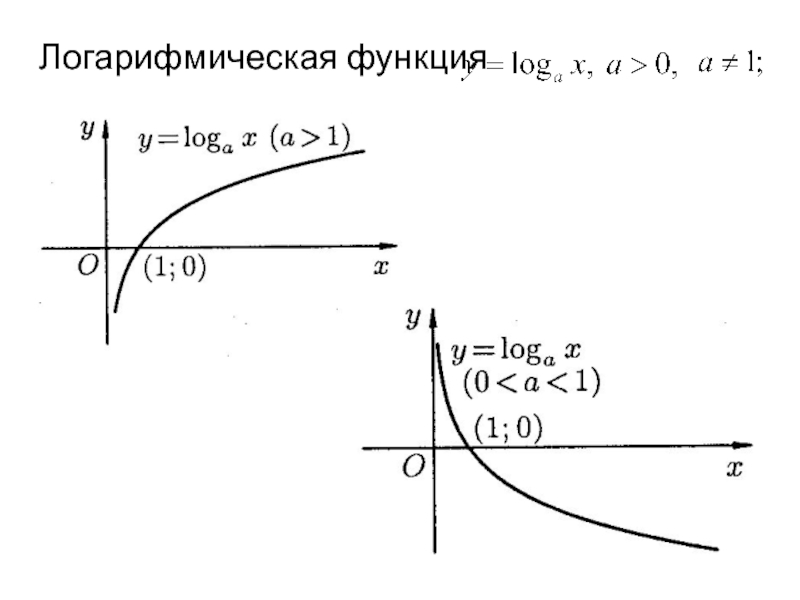
Логарифмическая функция
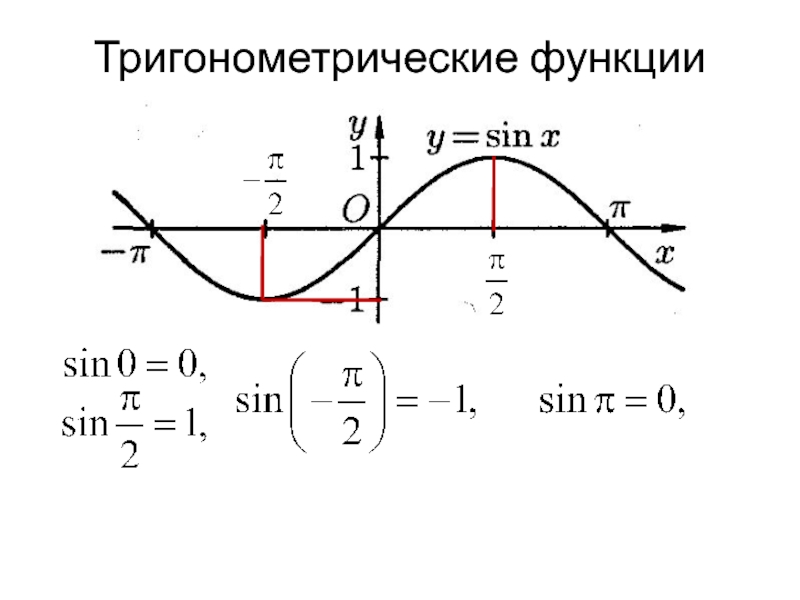
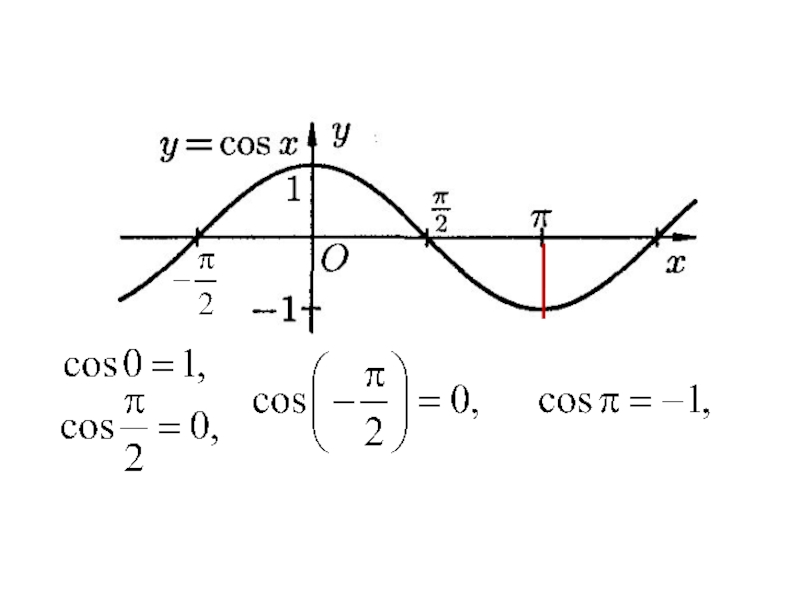
Тригонометрические функции
5) Обратные тригонометрические функции
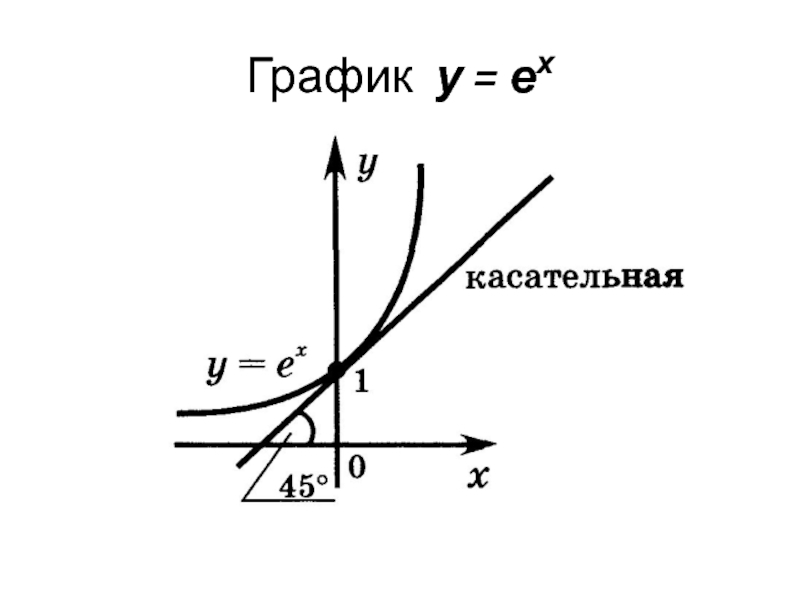
Слайд 29Показательная функция у = ех
Показательная функция у = ех,
где е =
2,71828 — число е,
называется экспоненциальной, или экспонентой.
у = ех = ехр(х) —
«экспонента от x».
называется экспоненциальной, или экспонентой.
у = ех = ехр(х) —
«экспонента от x».
Слайд 39 Элементарными функциями называются все функции, которые можно получить из основных элементарных
функций с помощью конечного числа арифметических действий с применением действительных коэффициентов и образования сложной функции.
Слайд 40Некоторые элементарные функции:
1) линейная функция
2) квадратичная функция
3) многочлены с
действительными коэффициентами (целые рациональные функции)
4) дробно-рациональные функции (рациональные дроби) – отношение многочленов:
4) дробно-рациональные функции (рациональные дроби) – отношение многочленов:
Слайд 415) иррациональные функции ‑ функции в которых используется операция извлечения корня.
Некоторые
неэлементарные функции:
1.
2. Дробная часть
1.
2. Дробная часть
Слайд 42Квадратичная функция
Квадратичной функцией называется функция вида
Область определения функции, т.е. все значения,
которые может принимать х, – все действительные числа.
Нули квадратичной функции – все значения х, при которых у=0, т.е. корни квадратного уравнения ах2+bх+с=0.
Нули квадратичной функции – все значения х, при которых у=0, т.е. корни квадратного уравнения ах2+bх+с=0.
Слайд 44 График функции
— парабола.
Вершина параболы —
точка .
Ось симметрии — прямая
Область значений — интервал , если
или , если
Вершина параболы —
точка .
Ось симметрии — прямая
Область значений — интервал , если
или , если
Слайд 45Свойства функции и вид ее графика определяются значениями коэффициента а и
дискриминанта D = b2 –4ас.
Слайд 48Определите:
a) максимальное и минимальное значение температуры;
b) в какое время температура была
равна нулю;
c) временные промежутки, на которых температура была положительная;
d) промежутки, на которых температура была отрицательная;
e) наибольший промежуток времени, на котором температура не меняла своего знака;
f) промежутки возрастания температуры;
g) промежутки убывания температуры.
c) временные промежутки, на которых температура была положительная;
d) промежутки, на которых температура была отрицательная;
e) наибольший промежуток времени, на котором температура не меняла своего знака;
f) промежутки возрастания температуры;
g) промежутки убывания температуры.
