- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Перпендикулярность прямой и плоскости презентация
Содержание
- 1. Перпендикулярность прямой и плоскости
- 2. Перпендикулярность прямой и плоскости
- 3. Дано: АВСДА1В1С1Д1 – параллелепипед,
- 4. Прямая перпендикулярная плоскости
- 5. Теоремы о связи между параллельностью прямых и
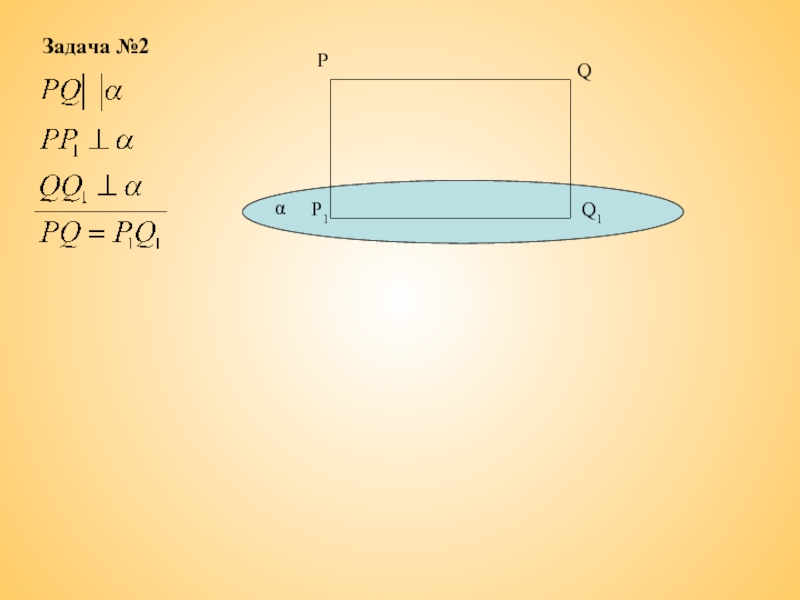
- 6. Задача №2
- 7. Признак перпендикулярности прямой и плоскости Доказательство
- 8. Построения I. Через любую точку пространства можно
- 9. Построения II. Через любую точку пространства можно
- 10. Построения Построение Единственность
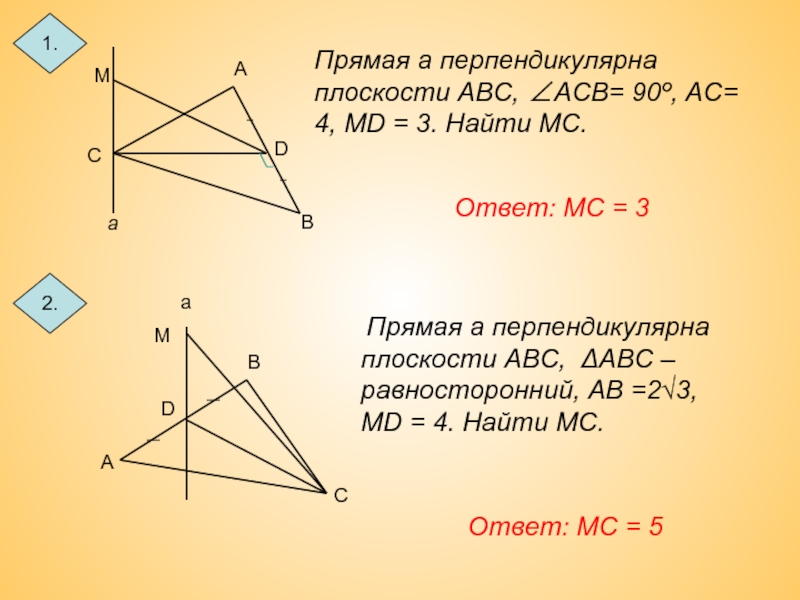
- 11. 1. 2. Ответ: МС = 3 Ответ: МС = 5
- 12. В тетраэдре DABC AD⊥AC, AD⊥AB, DC⊥CB.а)Докажите,
- 13. Точка Е не принадлежит плоскости прямоугольника АВСD,
- 14. Через катеты ВD и ВС прямоугольных треугольников
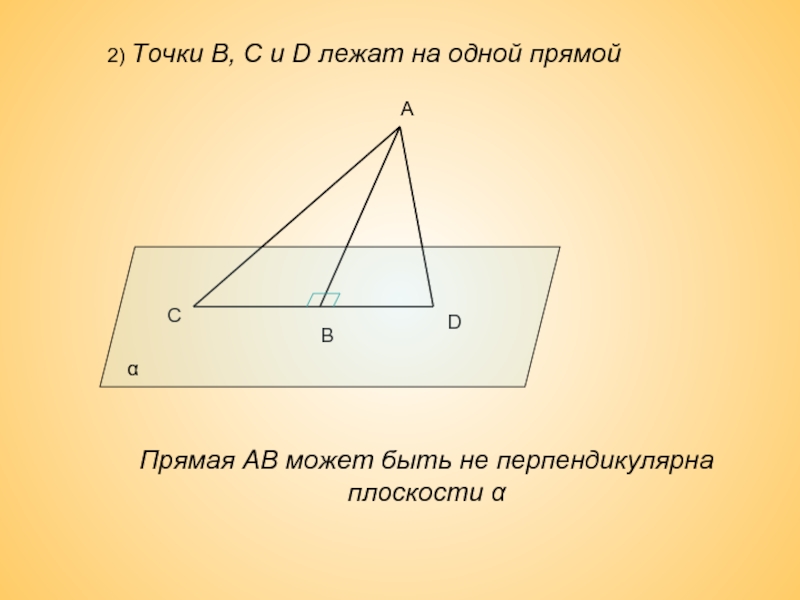
- 15. 2) Точки В, С и D лежат
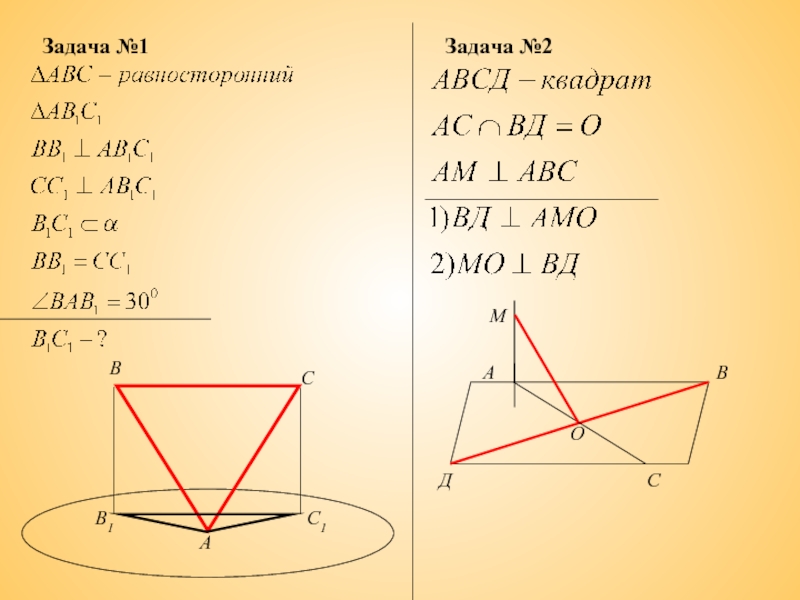
- 16. Задача №1 В В1 С С1 А Задача №2
- 17. Домашнее задание Глава 2. §1стр. теорию учить,
Слайд 2Перпендикулярность прямой и плоскости
Опр. Две прямые в пространстве называются
ними равен 90º.
Лемма Если одна из 2-х параллельных прямых,
перпендикулярна третьей прямой, то и
другая прямая перпендикулярна к этой
прямой.
М
с
Доказательство
Слайд 3
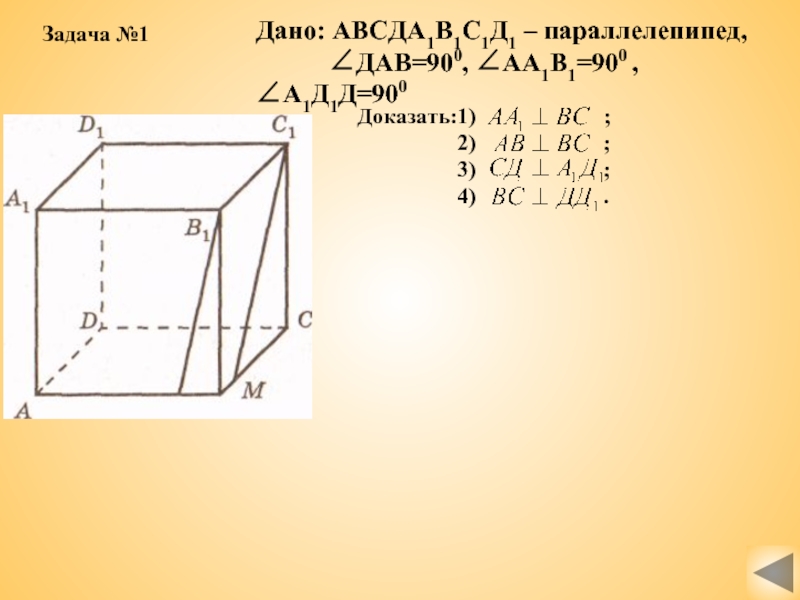
Дано: АВСДА1В1С1Д1 – параллелепипед,
∠ДАВ=900,
Доказать:1) ;
2) ;
3) ;
4) .
Задача №1
Слайд 4Прямая перпендикулярная плоскости
Опр. Прямая называется перпендикулярной плоскости,
к любой прямой, лежащей в этой плоскости.
Утверждение: Если прямая перпендикулярна плоскости, то она её пересекает.
Слайд 5Теоремы о связи между параллельностью прямых и их
Доказательство
Доказательство
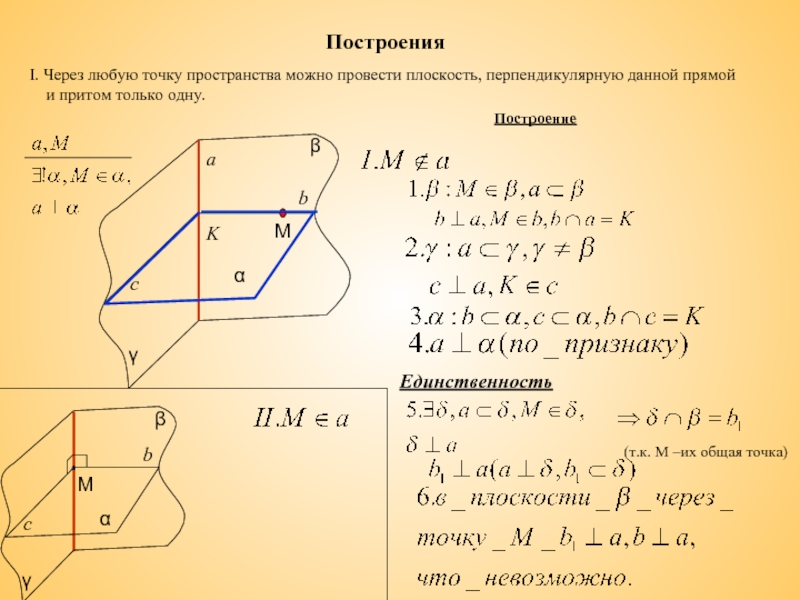
Слайд 8Построения
I. Через любую точку пространства можно провести плоскость, перпендикулярную данной прямой
М
K
Единственность
Построение
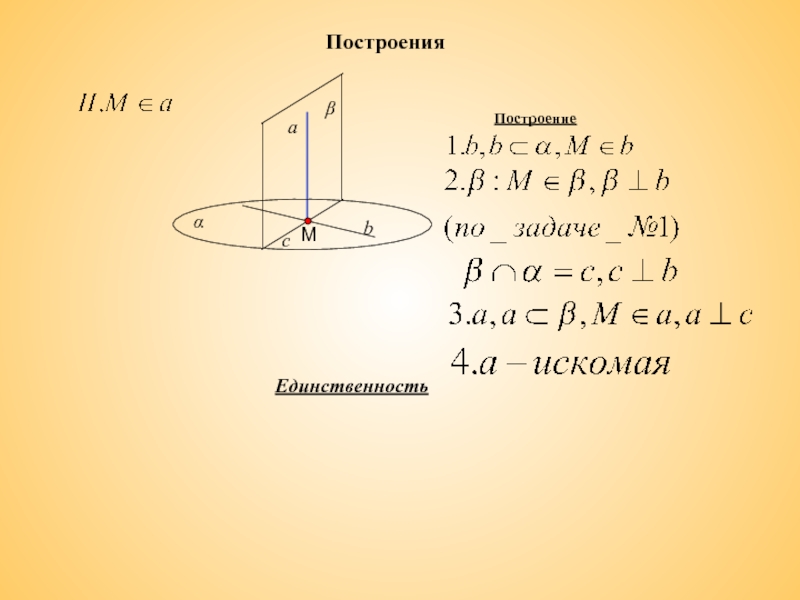
Слайд 9Построения
II. Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости
Построение
Единственность
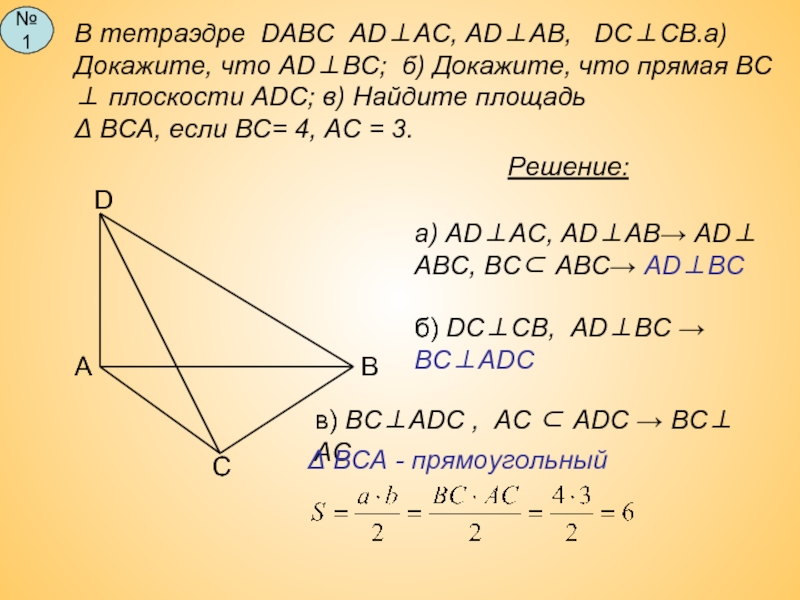
Слайд 12В тетраэдре DABC AD⊥AC, AD⊥AB, DC⊥CB.а)Докажите, что AD⊥ВC; б) Докажите,
№1
Решение:
а) AD⊥AC, AD⊥AB→ AD⊥ AВC, ВС⊂ АВС→ AD⊥ВС
б) DC⊥CB, AD⊥ВС → ВС⊥ADС
в) ВС⊥ADС , АС ⊂ АDС → ВС⊥ АС
Δ ВСА - прямоугольный
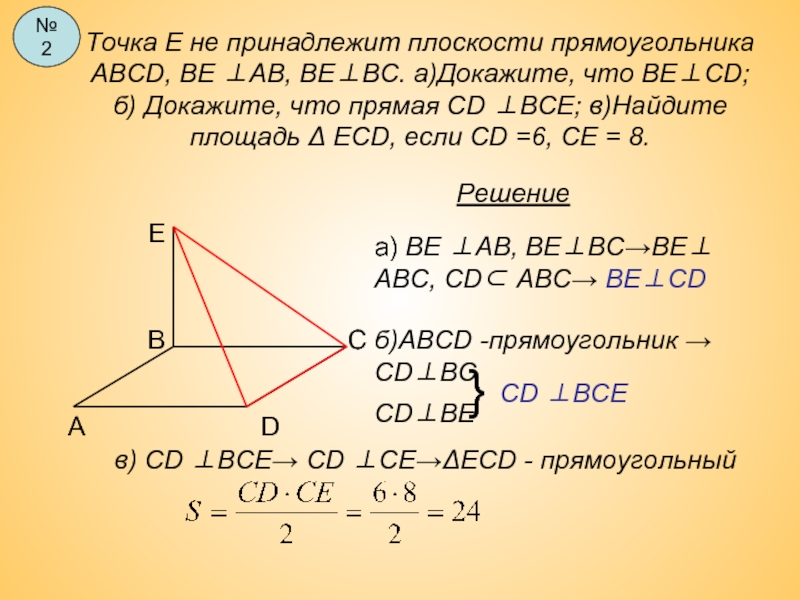
Слайд 13Точка Е не принадлежит плоскости прямоугольника АВСD, ВЕ ⊥AB, ВЕ⊥ВС. а)Докажите,
№2
Решение
а) ВЕ ⊥AB, ВЕ⊥ВС→ВЕ⊥ АВС, СD⊂ АВС→ ВЕ⊥CD
б)АВСD -прямоугольник → СD⊥BC
СD⊥ВЕ
}
СD ⊥ВСЕ
в) СD ⊥ВСЕ→ СD ⊥СЕ→ΔЕСD - прямоугольный
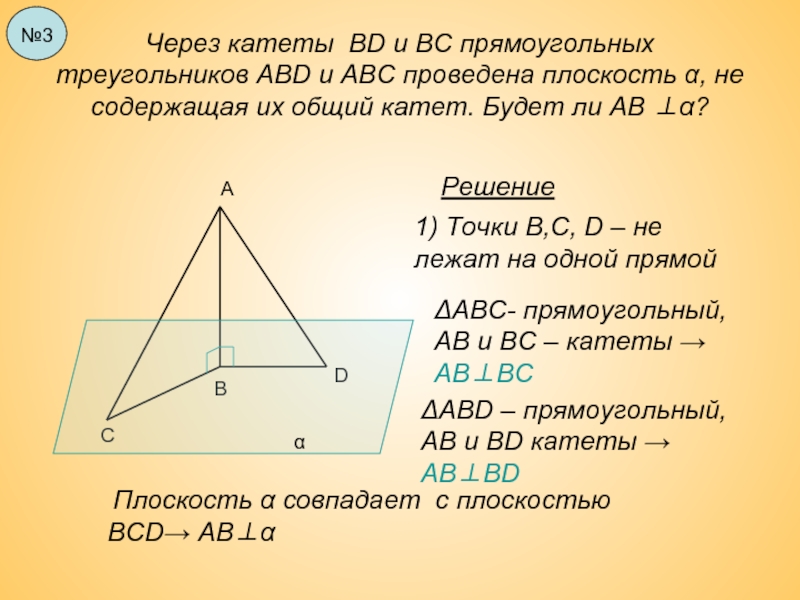
Слайд 14Через катеты ВD и ВС прямоугольных треугольников АВD и АВС проведена
№3
α
Решение
ΔABC- прямоугольный, АВ и ВС – катеты → AB⊥BC
ΔABD – прямоугольный, AB и BD катеты → AB⊥BD
Плоскость α совпадает с плоскостью BCD→ АВ⊥α
1) Точки В,С, D – не лежат на одной прямой