Пусть по результатам наблюдений изучается некоторая СВ.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия математической статистики презентация
Содержание
- 1. Основные понятия математической статистики
- 2. Основные задачи мат. статистики: — упорядочить исходные
- 3. п.2. Выборочный метод. Совокупность всех подлежащих исследованию
- 4. Пусть в выборке событие наблюдалось
- 5. Вариационным рядом называют таблицу вида: Статистическим распределением выборки (статистическим рядом) называют таблицу вида:
- 6. Пример. В результате тестирования группа студентов получила
- 7. Если число вариант велико или наблюдаемая СВ
- 8. Пример. Записать интервальный вариационный ряд.
- 9. Интервальный вариационный ряд:
- 10. п.3. Полигон и гистограмма. Полигоном частот называется
- 11. Для изучения непрерывного признака строится гистограмма. Гистограммой
- 12. Пример.
- 13. Гистограммой относительных частот называют ступенчатую фигуру, состоящую
- 14. п.4. Эмпирическая функция распределения. Эмпирической функцией распределения
- 15. Свойства эмпирической функции распределения 1) 2)
- 16. Пример. Вариационный ряд Построить эмпирическую функцию распределения.
- 17. Если , то Таким образом,
- 18. п.5. Статистические оценки. Пусть имеется некоторая выборка
- 19. Пусть последовательно производятся выборки объема n. Тогда
- 20. Оценка называется несмещенной, если ее
- 21. п.6. Числовые характеристики выборки. Рассмотрим вариационный ряд
- 22. Замечание. Выборочное среднее является несмещенной состоятельной оценкой
- 23. Замечание. Выборочное среднее является смещенной оценкой теоретической
- 24. Выборочным средним квадратическим отклонением называется квадратный корень
- 25. Начальным моментом r-го порядка называется среднее значение r-х степеней вариант При этом
- 26. Центральным моментом r-го порядка называется среднее значение
- 27. Модой Mo вариационного ряда называется варианта, имеющая
- 28. Эксцессом называется величина Замечание. Эксцесс характеризует степень
- 29. Пример. Вариационный ряд Найти числовые характеристики. Решение.
- 30. Объем выборки Выборочное среднее Выборочная дисперсия Выборочное среднее квадратическое отклонение
- 31. Исправленная выборочная дисперсия Исправленное выборочное среднее квадратическое отклонение Мода Медиана
- 32. Асимметрия Отрицательная асимметрия говорит о том,
- 33. Эксцесс Искомая кривая распределения имеет более острую вершину по сравнению с нормальным распределением.
Основные задачи мат. статистики: — упорядочить исходные данные (представить их в виде, удобном для анализа); — оценить требуемые характеристики наблюдаемой СВ (функцию распределения, мат. ожидание, дисперсию и т.д.); — проверить статистические
Слайд 1§8. Основные понятия математической статистики
п.1. Предмет математической статистики.
Математическая статистика изучает закономерности,
которым подчинены массовые случайные явления, с помощью методов ТВ.
Слайд 2Основные задачи мат. статистики:
— упорядочить исходные данные (представить их в виде,
удобном для анализа);
— оценить требуемые характеристики наблюдаемой СВ (функцию распределения, мат. ожидание, дисперсию и т.д.);
— проверить статистические гипотезы, т.е. решить вопрос согласования результатов оценивания с данными.
Слайд 3п.2. Выборочный метод.
Совокупность всех подлежащих исследованию объектов называется генеральной совокупностью.
Выборочной совокупностью
или случайной выборкой называют совокупность случайно отобранных объектов.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.
Слайд 4Пусть в выборке событие наблюдалось раз, событие
— раз и т.д., событие — раз.
Тогда объем выборки равен
Наблюдаемые значения называют вариантами.
Числа называют частотами.
Числа
называют относительными частотами.
Слайд 5Вариационным рядом называют таблицу вида:
Статистическим распределением выборки (статистическим рядом) называют таблицу
вида:
Слайд 6Пример. В результате тестирования группа студентов получила следующие оценки
Построить вариационный
и статистический ряд.
Решение.
Вариационный ряд.
Статистический ряд:
Слайд 7Если число вариант велико или наблюдаемая СВ является непрерывной, то поступают
следующим образом.
Вместо значений в первую строку вариационного (статистического) ряда записывают
(формула Стерджеса)
полуинтервалов длиной
Полученный ряд называют интервальным.
Слайд 8
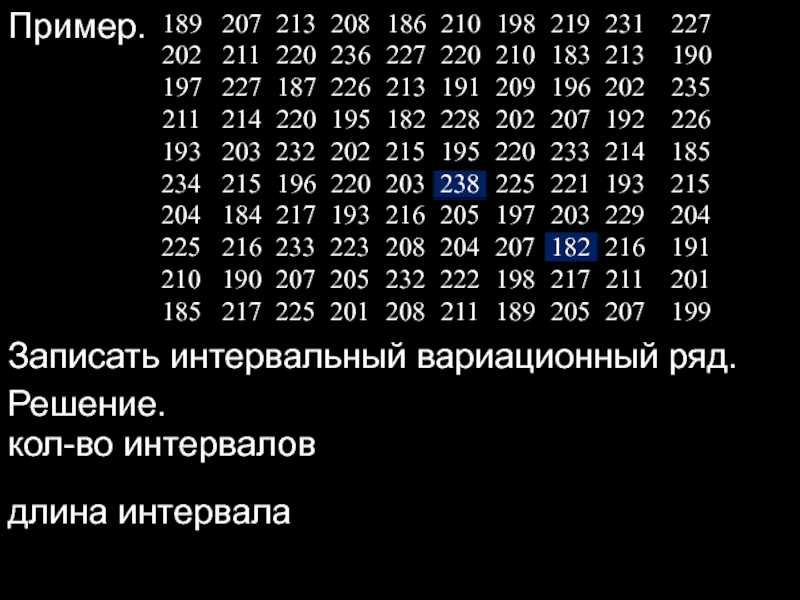
Пример.
Записать интервальный вариационный ряд.
Решение. Объем выборки
кол-во интервалов
длина интервала
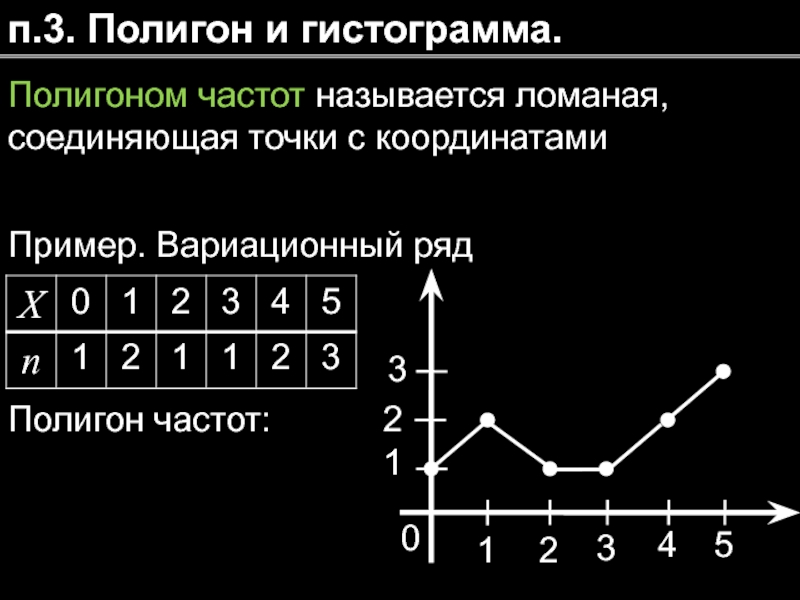
Слайд 10п.3. Полигон и гистограмма.
Полигоном частот называется ломаная, соединяющая точки с координатами
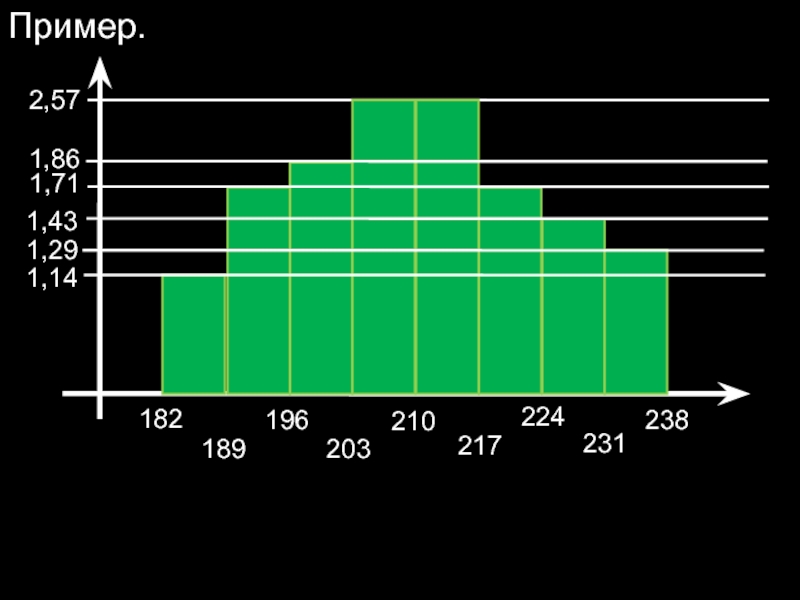
Пример.
Вариационный ряд
Полигон частот:
1
2
3
4
5
0
1
2
3
Слайд 11Для изучения непрерывного признака строится гистограмма.
Гистограммой частот называют ступенчатую фигуру, состоящую
из прямоугольников с основанием h и высотой
Замечание.
Площадь каждого прямоугольника:
Площадь всей гистограммы:
— объем выборки
Слайд 13Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников с основанием
h и высотой
Замечание.
Площадь каждого прямоугольника:
Площадь всей гистограммы:
Гистограмма относительных частот служит для оценки вида плотности вероятности.
Слайд 14п.4. Эмпирическая функция распределения.
Эмпирической функцией распределения называется функция, определяющая для каждого
значения x относительную частоту события
где — число вариант, меньших x,
n — объем выборки.
Слайд 15Свойства эмпирической функции распределения
1)
2) — неубывающая
функция.
3) Если — наименьшая варианта, то
Если — наименьшая варианта, то
Слайд 16Пример.
Вариационный ряд
Построить эмпирическую функцию распределения.
Решение. Объем выборки
Если
, то
Если , то
Если , то
Слайд 18п.5. Статистические оценки.
Пусть имеется некоторая выборка значений СВ, с теоретической функцией
распределения
Однако, вид этой функции неизвестен.
Требуется найти (оценить) какой-либо параметр этого распределения (мат. ожидание, дисперсию и т.д.).
Пусть — точное значение этого параметра (неизвестное).
Пусть — статистическая оценка параметра
Слайд 19Пусть последовательно производятся выборки объема n.
Тогда можно рассматривать как
СВ, принимающую значения
Для того, чтобы оценка давала хорошее приближение оцениваемому параметру она должна удовлетворять требованиям:
несмещенность;
эффективность;
состоятельность.
Слайд 20Оценка называется несмещенной, если ее мат. ожидание равно оцениваемому
параметру
Оценка называется эффективной, если ее дисперсия минимальна:
Оценка называется состоятельной, если при большом объеме выборки ее значение приближается к истинному:
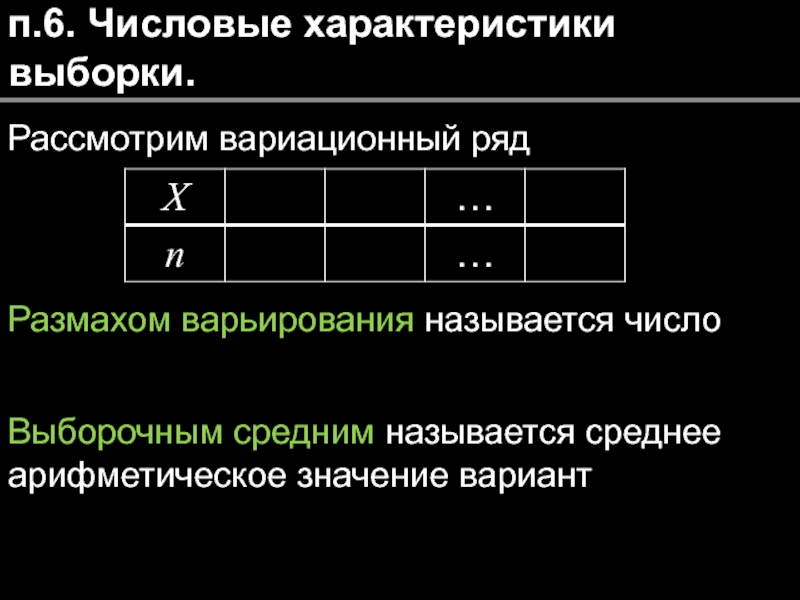
Слайд 21п.6. Числовые характеристики выборки.
Рассмотрим вариационный ряд
Размахом варьирования называется число
Выборочным средним называется
среднее арифметическое значение вариант
Слайд 22Замечание.
Выборочное среднее является несмещенной состоятельной оценкой математического ожидания.
Выборочной дисперсией называется среднее
значение квадратов отклонения вариант от выборочного среднего
Несложно получить, что
Слайд 23Замечание.
Выборочное среднее является смещенной оценкой теоретической дисперсии.
Можно показать, что
В качестве несмещенной
оценки дисперсии используется исправленная выборочная дисперсия
Слайд 24Выборочным средним квадратическим отклонением называется квадратный корень из выборочной дисперсии
Исправленным выборочным
средним квадратическим отклонением называется величина S (корень из ).
Замечание.
Выборочное среднее и выборочная дисперсия обладают теми же свойствами, что и мат. ожидание и дисперсия дискретной СВ.
Слайд 26Центральным моментом r-го порядка называется среднее значение отклонений в степени r
среднего
При этом
Слайд 27Модой Mo вариационного ряда называется варианта, имеющая наибольшую частоту.
Модой Me вариационного
ряда называется варианта, которая делит ряд на две части, равные по числу вариант.
Асимметрией называется величина
Замечание.
Асимметрия характеризует меру симметричности эмпирической кривой распределения относительно среднего значения.
Для нормального распределения
Слайд 28Эксцессом называется величина
Замечание.
Эксцесс характеризует степень островершинности эмпирической кривой распределения по сравнению
с нормальной кривой.
Для нормального распределения
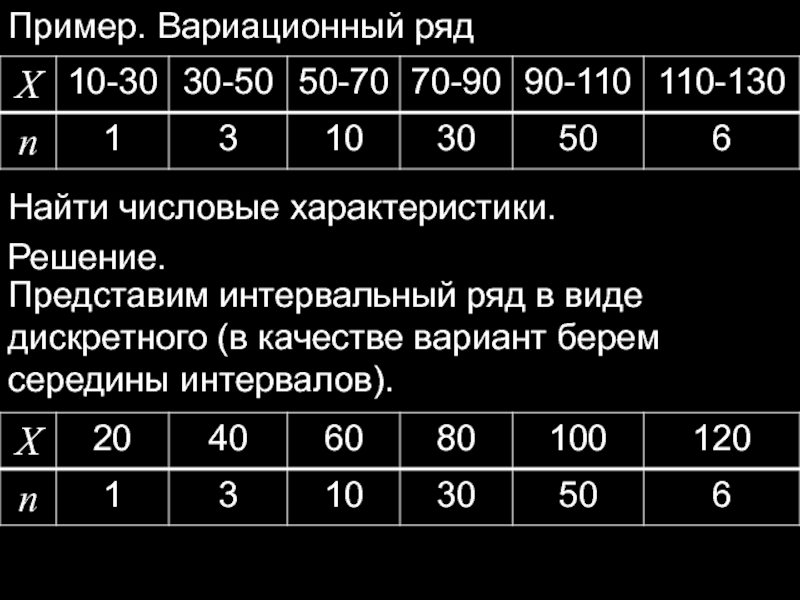
Слайд 29Пример.
Вариационный ряд
Найти числовые характеристики.
Решение.
Представим интервальный ряд в виде дискретного (в качестве
вариант берем середины интервалов).
Слайд 30Объем выборки
Выборочное среднее
Выборочная дисперсия
Выборочное среднее квадратическое отклонение
Слайд 31Исправленная выборочная дисперсия
Исправленное выборочное среднее квадратическое отклонение
Мода
Медиана
Слайд 32Асимметрия
Отрицательная асимметрия говорит о том, что в вариационном ряде преобладают варианты,
меньшие выборочного среднего.
Слайд 33Эксцесс
Искомая кривая распределения имеет более острую вершину по сравнению с нормальным
распределением.
