- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Осевая симметрия. (8 класс) презентация
Содержание
- 1. Осевая симметрия. (8 класс)
- 2. Содержание Симметрия Осевая симметрия Задачи Симметрия в геометрии, природе, архитектуре, поэзии Заключение
- 3. Определение Симметрия (от греч. Symmetria – соразмерность),
- 4. Осевая симметрия Две точки, лежащие на одном
- 5. Фигура называется симметричной относительно прямой a, если
- 6. Фигуры, обладающие одной осью симметрии Угол Равнобедренный треугольник Равнобедренная трапеция
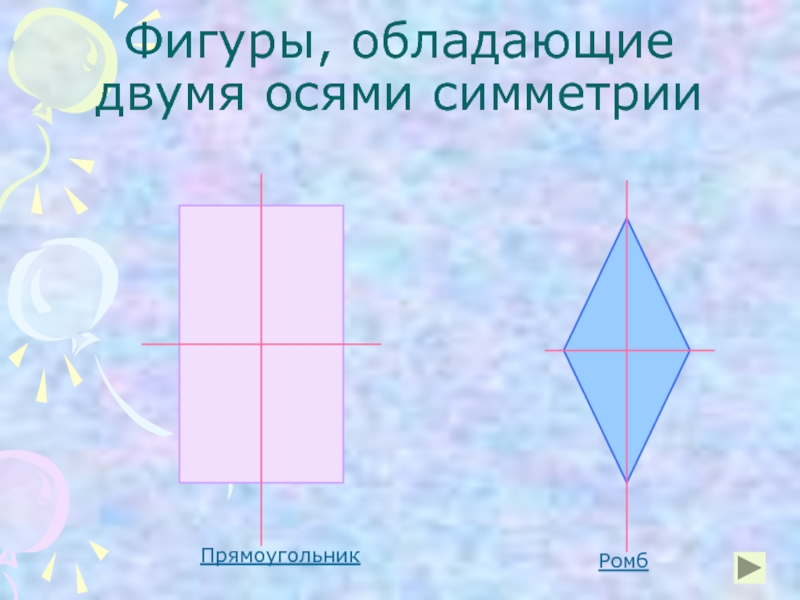
- 7. Фигуры, обладающие двумя осями симметрии Прямоугольник Ромб
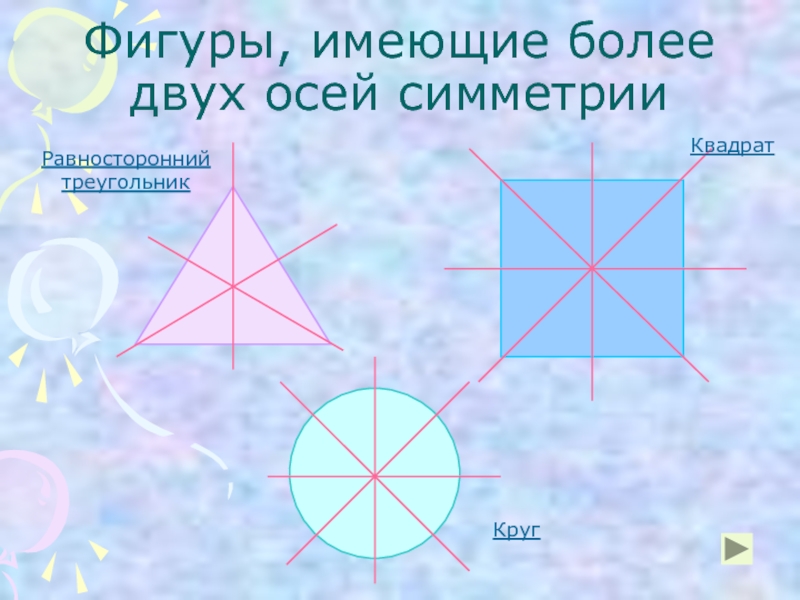
- 8. Фигуры, имеющие более двух осей симметрии Равносторонний треугольник Квадрат Круг
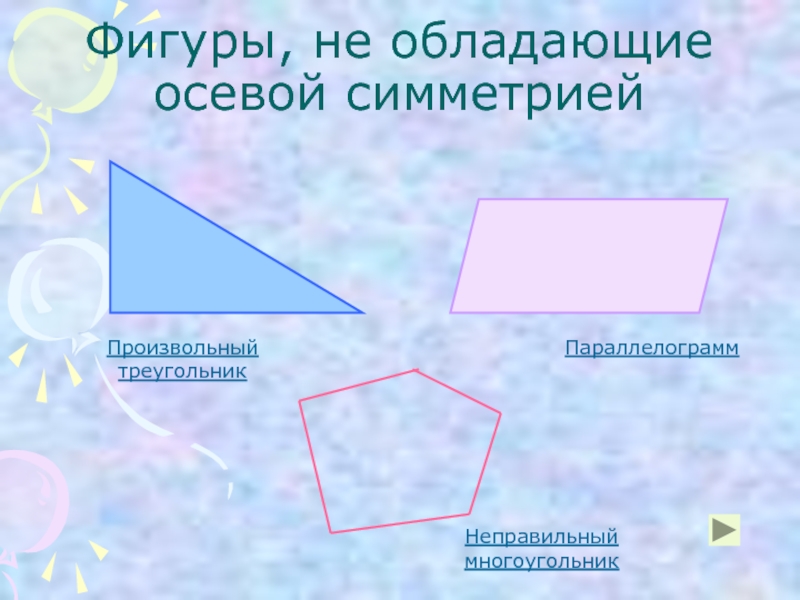
- 9. Фигуры, не обладающие осевой симметрией Произвольный треугольник Параллелограмм Неправильный многоугольник
- 10. Построение точки, симметричной данной отрезка, симметричного данному треугольника, симметричного данному
- 11. Построение точки, симметричной данной А с
- 12. Построение отрезка, симметричного данному А с
- 13. Построение треугольника, симметричного данному А с
- 14. Задачи 1. Отрезок АВ, перпендикулярный прямой с,
- 15. Задачи 1. Отрезок АВ, перпендикулярный прямой с,
- 16. 4. Изобразите точку А, лежащую в I
- 17. Ответ: Точки A и D симметричны
- 18. 5. Относительно какой из координатных осей симметричны
- 19. Проверь себя 5. Ответ: Оу.
- 20. 9. Для каждого из случаев, представленных на
- 21. 9. Для каждого из случаев, представленных на
- 22. 10. Постройте треугольники, симметричные данным, относительно прямой с. с с
- 23. 10. Постройте треугольники, симметричные данным, относительно прямой с. с с
- 24. 11. Начертите две прямые а и b
- 25. Подсказка Для решения задачи рекомендуется сначала отметить
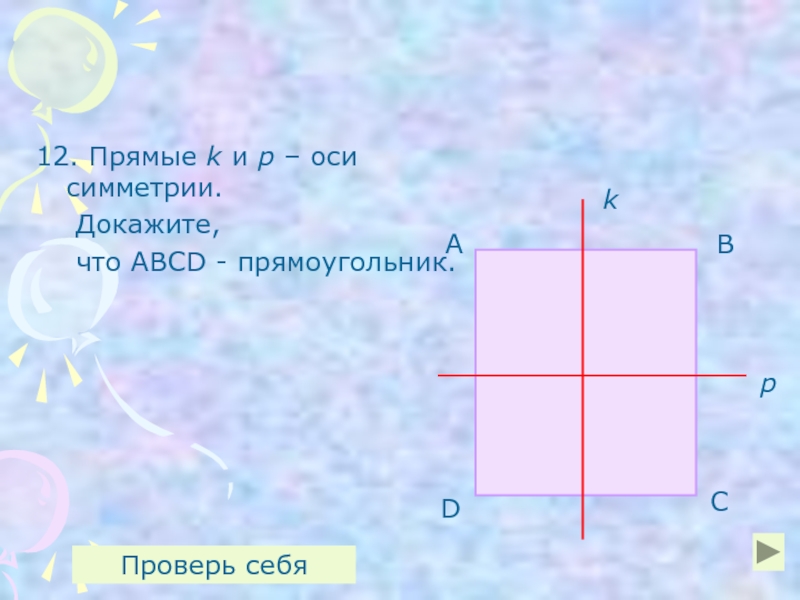
- 26. 12. Прямые k и р – оси
- 27. Доказательство: Так как k –
- 28. Симметрия в природе
- 29. В архитектуре
- 30. Пушкин А.С. «Медный всадник» …В гранит оделася
- 31. Заключение Симметрию можно обнаружить почти везде, если
Содержание Симметрия Осевая симметрия Задачи Симметрия в геометрии, природе, архитектуре, поэзии Заключение
Слайд 2Содержание
Симметрия
Осевая симметрия
Задачи
Симметрия в геометрии, природе, архитектуре, поэзии
Заключение
Слайд 3Определение
Симметрия (от греч. Symmetria – соразмерность), в широком смысле – неизменность
структуры материального объекта относительно его преобразований. Симметрия играет огромную роль в искусстве и архитектуре. Но ее можно заметить и в музыке, и в поэзии. Симметрия широко встречается в природе, в особенности у кристаллов, у растений и животных. Симметрия может встретиться и в других разделах математики, например при построении графиков функций.
Слайд 4Осевая симметрия
Две точки, лежащие на одном перпендикуляре к данной прямой по
разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно данной прямой.
Слайд 5Фигура называется симметричной относительно прямой a, если для каждой точки фигуры
симметричная ей точка относительно прямой а также принадлежит этой фигуре.
а
А
В
Слайд 9Фигуры, не обладающие осевой симметрией
Произвольный треугольник
Параллелограмм
Неправильный многоугольник
Слайд 10Построение
точки, симметричной данной
отрезка, симметричного данному
треугольника, симметричного данному
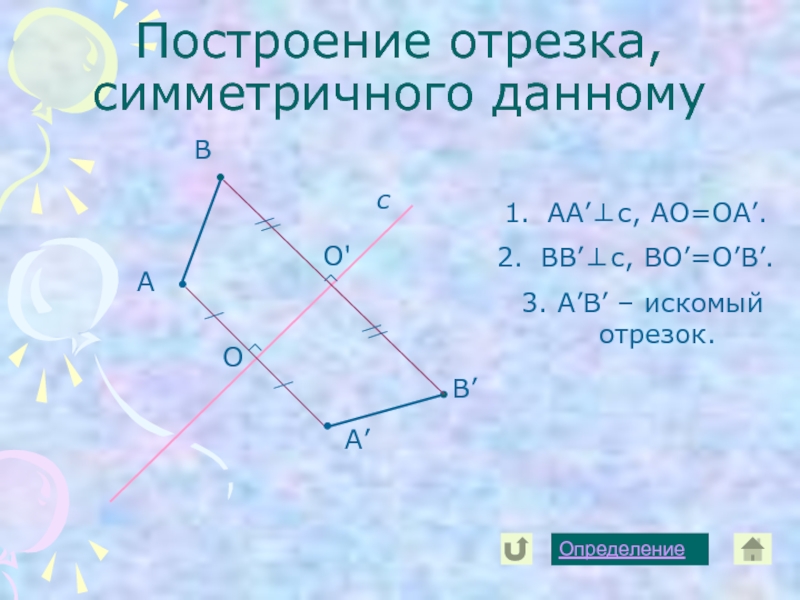
Слайд 12Построение отрезка, симметричного данному
А
с
А’
В
В’
Определение
O
O'
АА’⊥с, АО=ОА’.
ВВ’⊥с, ВО’=О’В’.
3. А’В’ – искомый отрезок.
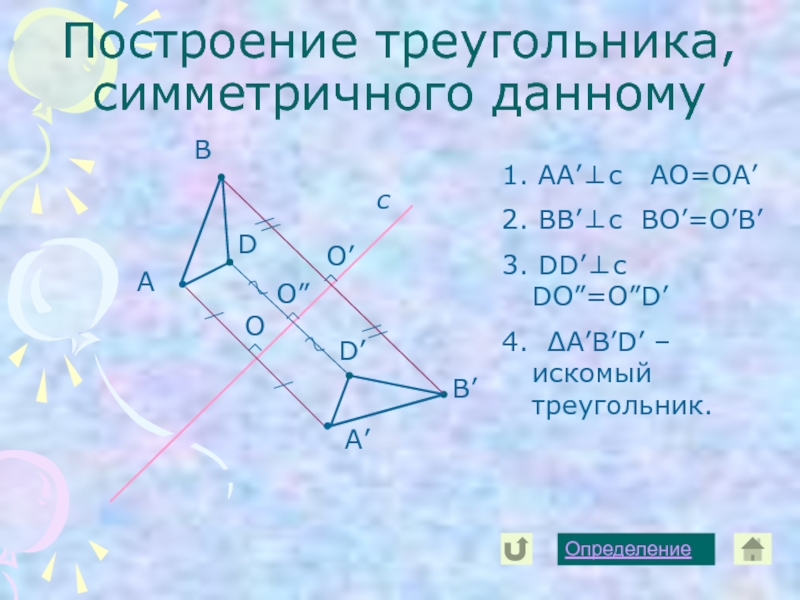
Слайд 13Построение треугольника, симметричного данному
А
с
А’
В
В’
D
D’
Определение
1. AA’⊥c AO=OA’
2. BB’⊥c BO’=O’B’
3. DD’⊥c DO”=O”D’
4.
ΔA’B’D’ – искомый треугольник.
O
O”
O’
Слайд 14Задачи
1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О
так, что АО≠ОВ. Симметричны ли точки А и В относительно прямой с?
2. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а?
3. Точки А и В расположены в различных полуплоскостях с границей р так, что отрезок АВ перпендикулярен прямой р и делится ею пополам. Симметричны ли точки А и В относительно прямой р?
2. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а?
3. Точки А и В расположены в различных полуплоскостях с границей р так, что отрезок АВ перпендикулярен прямой р и делится ею пополам. Симметричны ли точки А и В относительно прямой р?
Слайд 15Задачи
1. Отрезок АВ, перпендикулярный прямой с, пересекает ее в точке О
так, что АО≠ОВ. Симметричны ли точки А и В относительно прямой с?
Ответ: нет
2. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а?
Ответ: нет
3. Точки А и В расположены в различных полуплоскостях с границей р так, что отрезок АВ перпендикулярен прямой р и делится ею пополам. Симметричны ли точки А и В относительно прямой р?
Ответ: да
Ответ: нет
2. Прямая а пересекает отрезок МК в его середине под углом, отличным от прямого. Симметричны ли точки М и К относительно прямой а?
Ответ: нет
3. Точки А и В расположены в различных полуплоскостях с границей р так, что отрезок АВ перпендикулярен прямой р и делится ею пополам. Симметричны ли точки А и В относительно прямой р?
Ответ: да
Слайд 164. Изобразите точку А, лежащую в I четверти
координатной плоскости.
Точка В
симметрична точке А относительно оси y.
Точка С симметрична точке В относительно оси х.
Точка D симметрична точке С относительно оси у.
Что вы можете сказать:
о точках A и D
о фигуре ABCD
при каком условии ABCD будет квадратом
Точка С симметрична точке В относительно оси х.
Точка D симметрична точке С относительно оси у.
Что вы можете сказать:
о точках A и D
о фигуре ABCD
при каком условии ABCD будет квадратом
Слайд 17Ответ:
Точки A и D симметричны относительно оси х.
ABCD – прямоугольник
Если расстояния
от точки А до оси х и у будут равными
Слайд 185. Относительно какой из координатных осей симметричны точки М(7;2) и К(-7;2)?
6.
Точки А(5;…) и В(…;2) симметричны относительно оси Ох. Запишите их пропущенные координаты.
7. Точка А(-2;3), В - симметричная ей точка относительно оси Ох, точка С – симметричная точке В относительно оси Оу. Найдите координаты точки С.
8. Точка А(3;1), В – симметричная ей точка относительно прямой у = х. Найдите координаты точки В.
7. Точка А(-2;3), В - симметричная ей точка относительно оси Ох, точка С – симметричная точке В относительно оси Оу. Найдите координаты точки С.
8. Точка А(3;1), В – симметричная ей точка относительно прямой у = х. Найдите координаты точки В.
Проверь себя
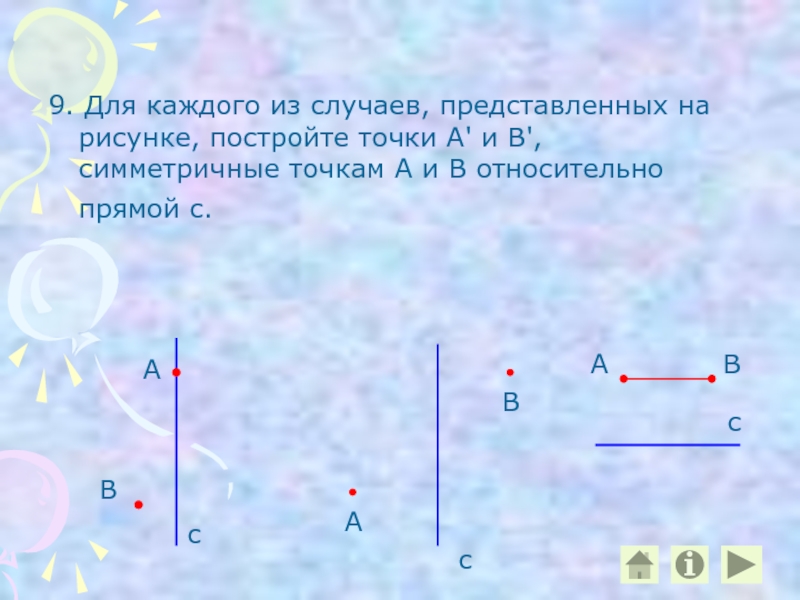
Слайд 209. Для каждого из случаев, представленных на рисунке, постройте точки А'
и В', симметричные точкам А и В относительно прямой с.
В
А
с
А
В
с
А
В
с
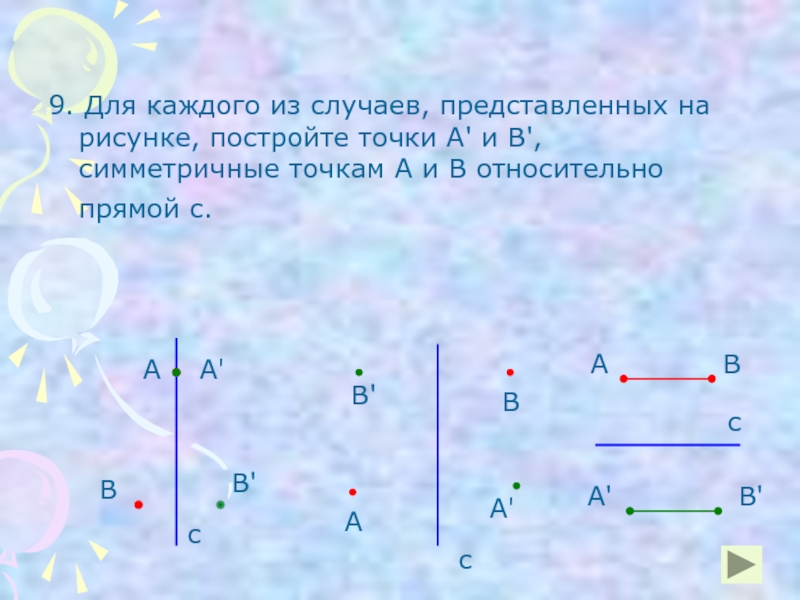
Слайд 219. Для каждого из случаев, представленных на рисунке, постройте точки А'
и В', симметричные точкам А и В относительно прямой с.
В
В'
А
А'
с
А
А'
В
В'
с
А
В
с
А'
В'
Слайд 2411. Начертите две прямые а и b и отметьте две точки
А и В так, чтобы точка С была симметрична точке А относительно прямой а, а точке В относительно прямой b.
Слайд 25Подсказка
Для решения задачи рекомендуется сначала отметить точку С, а лишь потом
отмечать точки А и В.
Слайд 27
Доказательство:
Так как k – ось симметрии, то ∠А=∠D, ∠В=∠С. Так как
р – ось симметрии, то ∠А=∠В, ∠С=∠D. Тогда ∠А=∠В=∠С=∠D=90°.
АВСD – прямоугольник.
АВСD – прямоугольник.
Слайд 30Пушкин А.С. «Медный всадник»
…В гранит оделася Нева;
Мосты повисли над водами;
Темнозелеными садами
Ее
покрылись острова…
Симметрия в поэзии
Слайд 31Заключение
Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие
народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».
