- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистика. Статистическая сводка презентация
Содержание
- 1. Статистика. Статистическая сводка
- 2. Статистическая сводка - это комплекс последовательных
- 3. Виды группировок ТИПОЛОГИЧЕСКИЕ
- 4. Группировочным признаком называется признак, по которому
- 5. Если вариация признака проявляется в сравнительно
- 6. Простейшая группировка, в
- 7. Частотами называются численности отдельных
- 8. Формы вариационного ряда Ранжированный вариационный
- 9. Задача. Имеется
- 10. Решение
- 11. Задача.
- 12. Решение Для
- 14. Задача
- 15. Произведите группировку предприятий
- 16. Решение Для
- 18. Вывод: Как видно
- 19. Средние величины
- 20. Средняя арифметическая
- 21. Средние величины
- 22. Средние величины
- 23. Средние величины
- 24. Средние величины
- 25. Средние величины
- 26. Средние величины
- 27. Средние величины
- 28. Задача.
- 29. Решение. Поскольку
- 30. Средний процент кандидатов
- 31. Задача Дан
- 32. Задача
- 33. Решение Для решения
- 34. Задача. Сумма
- 35. Задача. Распределение рабочих
- 36. fMo-1 = 20
- 37. Задача По данным
- 38. Решение: Определим
- 39. 2) Определим для
- 40. 2-й район M0=2
- 41. Задача По
- 42. Определим медианный интервал.
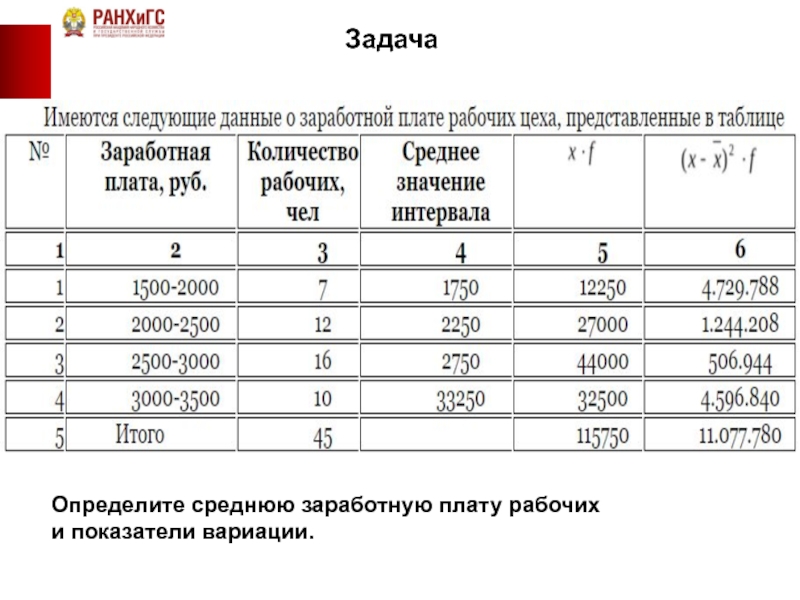
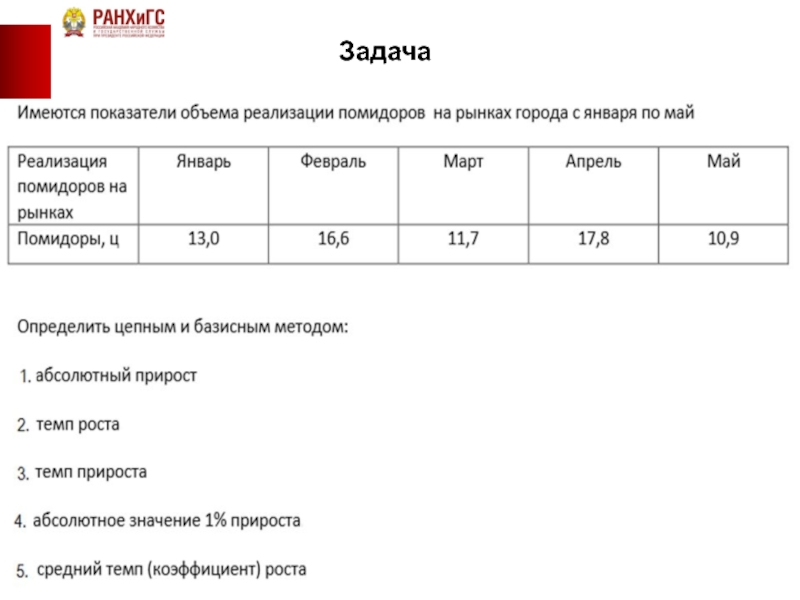
- 43. Задача Определите среднюю заработную плату рабочих и показатели вариации.
- 45. Коэффициент вариации Из
- 46. Задача
- 47. Решение
- 50. Экономические индексы
- 51. Экономические индексы
- 52. Экономические индексы
- 53. Экономические индексы
- 54. Экономические индексы в статистике
- 55. Экономические индексы
- 56. Экономические индексы
- 57. Экономические индексы
- 58. Решение 1)
- 59. (12*15+20*10+12*8)/470 = 476/470
- 60. 3) абсолютное изменение
- 61. Экономические индексы
- 62. Решение 1)
- 63. (22+10,44+18,75)/(20+12+15)=51,19/47=1,089=108,9% 3) Поскольку
- 64. Абсолютные и
- 65. Абсолютные и
- 66. Абсолютные и
- 67. Все используемые на
- 68. Абсолютные и
- 69. Доля городского
- 70. 2) Относительный показатель
- 77. Спасибо за внимание!
Слайд 2
Статистическая сводка - это комплекс последовательных операций по обобщению конкретных единичных
Проведение статистической сводки включает следующие этапы:
- выбор группировочного признака;
- определение порядка формирования групп;
- разработка системы статистических показателей для характеристики групп и объекта в целом;
- разработка макетов статистических таблиц для представления результатов сводки.
Слайд 4
Группировочным признаком называется признак, по которому проводится разбиение единиц совокупности на
Интервал - это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них.
Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей - наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами.
Интервалы группировки в зависимости от их величины бывают: равные и неравные.
Слайд 5
Если вариация признака проявляется в сравнительно узких границах и распределение носит
где Хmax, Хmin - максимальное и минимальное значения
признака в совокупности;
n - число групп.
Слайд 6
Простейшая группировка, в которой каждая выделенная группа характеризуется одним показателем представляет
Статистический ряд распределения - это упорядоченное распределение единиц совокупности на группы по определенному признаку. В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам, то есть признакам, не имеющим числового выражения. Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры.
Вариационными рядами называют ряды распределения, построенные по количественному признаку. Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака.
Слайд 7
Частотами называются численности отдельных вариант или каждой группы вариационного ряда, то есть
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
Слайд 8
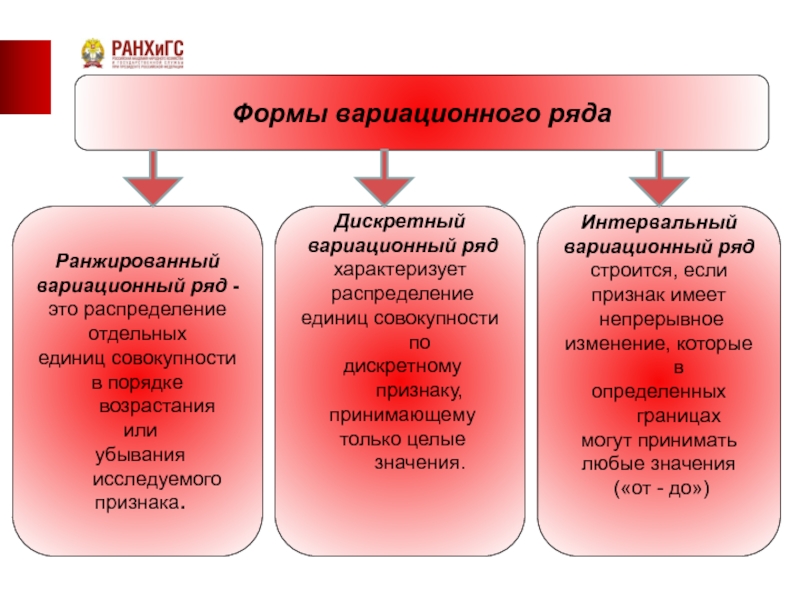
Формы вариационного ряда
Ранжированный
вариационный ряд -
это распределение
отдельных
единиц совокупности
в
или
убывания исследуемого
признака.
Дискретный
вариационный ряд
характеризует
распределение
единиц совокупности по
дискретному признаку,
принимающему
только целые значения.
Интервальный
вариационный ряд
строится, если
признак имеет
непрерывное
изменение, которые в
определенных границах
могут принимать
любые значения
(«от - до»)
Слайд 9
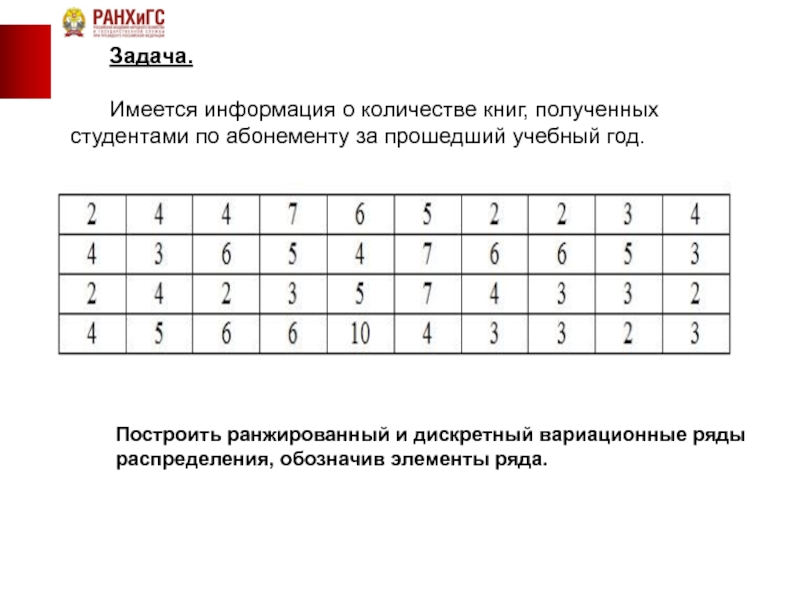
Задача.
Имеется информация о количестве книг, полученных студентами по абонементу за прошедший
Построить ранжированный и дискретный вариационные ряды
распределения, обозначив элементы ряда.
Слайд 11
Задача.
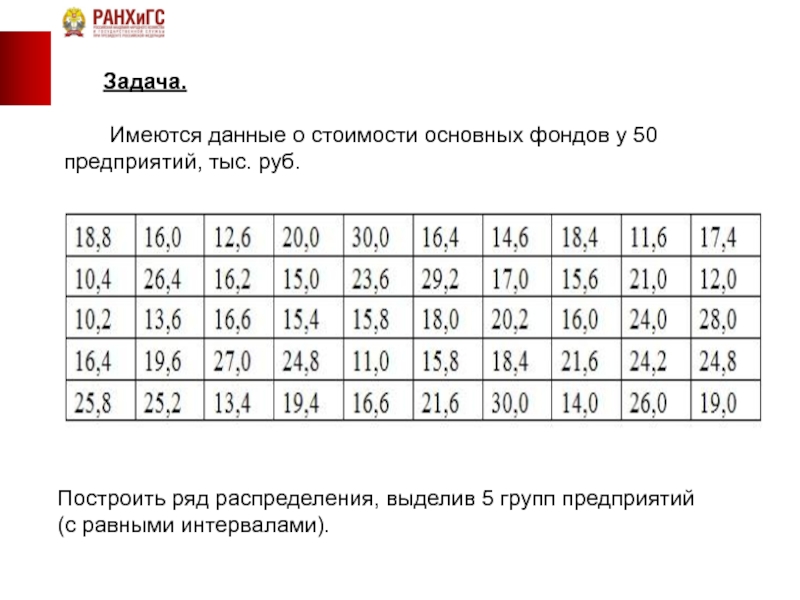
Имеются данные о стоимости основных фондов у 50 предприятий, тыс.
Построить ряд распределения, выделив 5 групп предприятий
(с равными интервалами).
Слайд 12
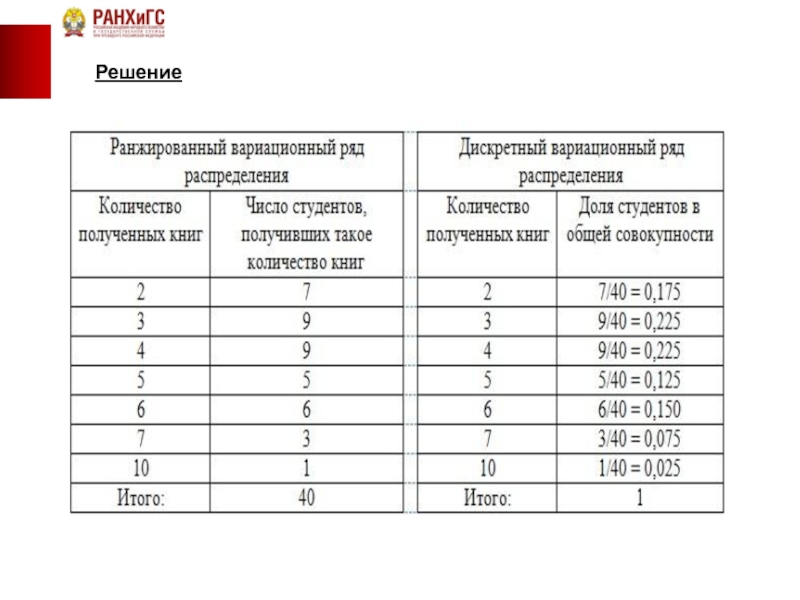
Решение
Для решения выберем наибольшее и наименьшее значения стоимости основных фондов предприятий.
Найдем размер интервала:
h = (30,0-10,2):5= 3,96 тыс. руб.
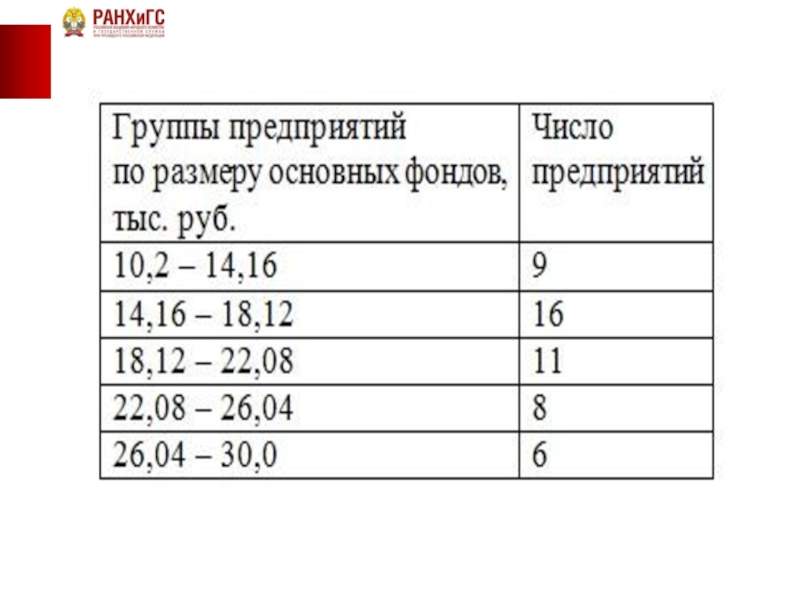
Тогда в первую группу будут входить предприятия, размер основных фондов которых составляет от 10,2 тыс. руб. до 10,2+3,96=14,16 тыс. руб.
Таких предприятий будет 9.
Во вторую группу войдут предприятия, размер основных фондов которых составит от 14,16 тыс. руб. до 14,16+3,96=18,12 тыс. руб. Таких предприятий будет 16. Аналогично найдем число предприятий, входящих в третью, четвертую и пятую группы.
Слайд 15
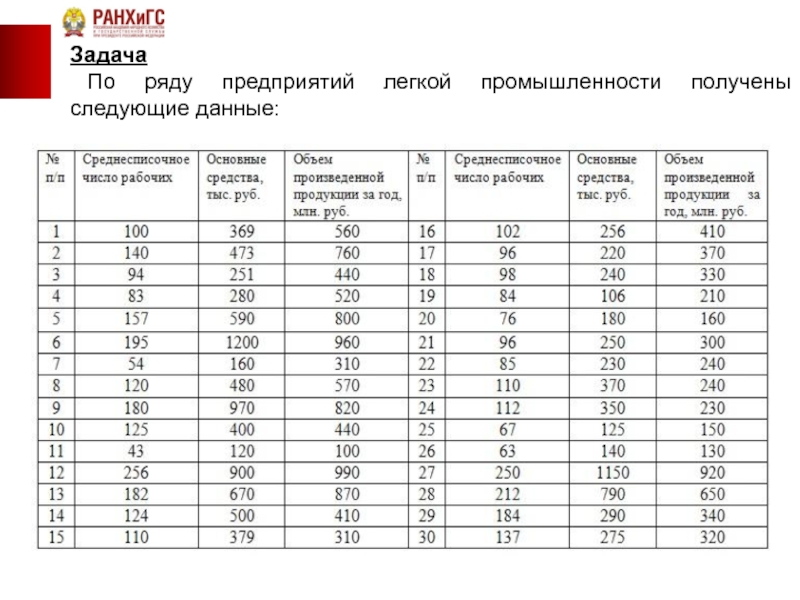
Произведите группировку предприятий по числу рабочих, образуя 6 групп с равными
число предприятий
число рабочих 3. объем произведенной продукции за год 4. среднюю фактическую выработку одного рабочего 5. объем основных средств 6. средний размер основных средств одного предприятия 7. среднюю величину произведенной продукции одним предприятием
Результаты расчета оформите в таблицы. Сделайте выводы.
Слайд 16
Решение
Для решения выберем наибольшее и наименьшее значения среднесписочного числа рабочих на
Найдем размер интервала:
h = (256-43):6 = 35,5
Тогда в первую группу будут входить предприятия, среднесписочное число рабочих на которых составляет от 43 до 43+35,5=78,5 человек. Таких предприятий будет 5.
Во вторую группу войдут предприятия, среднесписочное число рабочих на которых составит от 78,5 до 78,5+35,5=114 человек. Таких предприятий будет 12.
Аналогично найдем число предприятий, входящих в третью, четвертую, пятую и шестую группы.
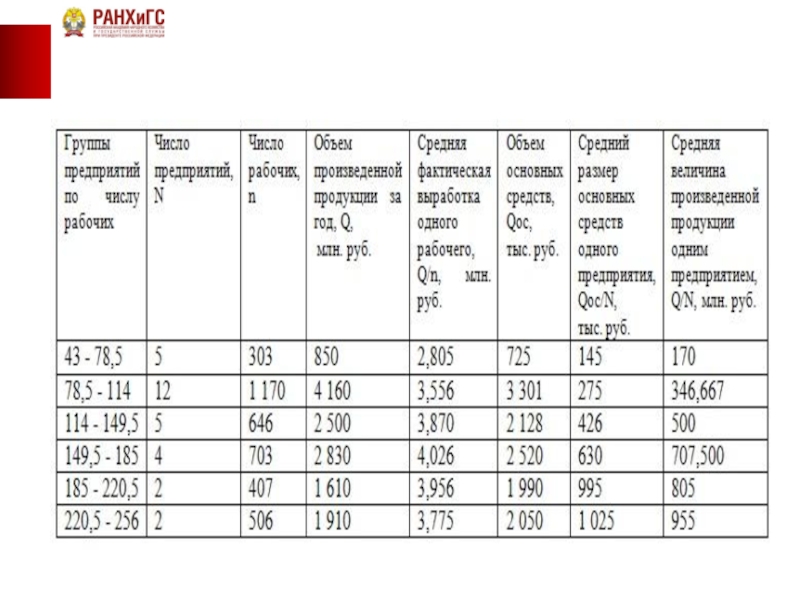
Полученный ряд распределения поместим в таблицу и вычислим необходимые показатели по каждой группе:
Слайд 18
Вывод: Как видно из таблицы, вторая группа предприятий является самой многочисленной.
Поскольку вторая группа самая многочисленная, объем произведенной продукции за год предприятиями этой группы и объем основных средств значительно выше других. Вместе с тем средняя фактическая выработка одного рабочего на предприятиях этой группы наибольшей не является. Здесь лидируют предприятия четвертой группы. На эту группу приходится и довольно большой объем основных средств.
В заключении отметим, что средний размер основных средств и средняя величина произведенной продукции одного предприятия прямо пропорциональны размерам предприятия (по числу рабочих).
Слайд 19
Средние величины в статистике
Средняя величина представляет обобщенную количественную характеристику признака в
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности, ведь значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть и случайные.
Слайд 20
Средняя арифметическая простая:
Средняя арифметическая простая используется в тех случаях, когда расчет
Средние величины в статистике
где хi – варианты,
Слайд 21
Средние величины в статистике
Средняя арифметическая взвешенная
При расчете средних величин отдельные
где хi – варианты,
fi – частоты или веса.
Слайд 22
Средние величины в статистике
Средняя гармоническая простая
Средние гармонические используются тогда, когда
Слайд 23
Средние величины в статистике
Средняя гармоническая взвешенная
Данная формула используется для расчета
Слайд 24
Средние величины в статистике
Средняя геометрическая простая (невзвешенная)
Наиболее широкое применение этот вид
Слайд 25
Средние величины в статистике
Средняя квадратическая простая (невзвешенная)
Средняя квадратическая лежит в
Слайд 26
Средние величины в статистике
Структурные средние
Мода (Мо) представляет собой значение изучаемого признака,
Для интервального ряда расчет моды осуществляется по формуле:
где
Хо - нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
i - величина модального интервала;
f Мо - частота модального интервала;
f Мо-1 - частота интервала, предшествующего модальному;
f Мо+1 - частота интервала, следующего за модальным.
Слайд 27
Средние величины в статистике
Структурные средние
Медианой (Ме) называется значение признака, приходящееся на
Для интервального ряда расчет медианы осуществляется по формуле:
Хо - нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);
i - величина медианного интервала;
Sme-1 - накопленная частота интервала, предшествующего медианному;
f Me - частота медианного интервала.
Слайд 28
Задача.
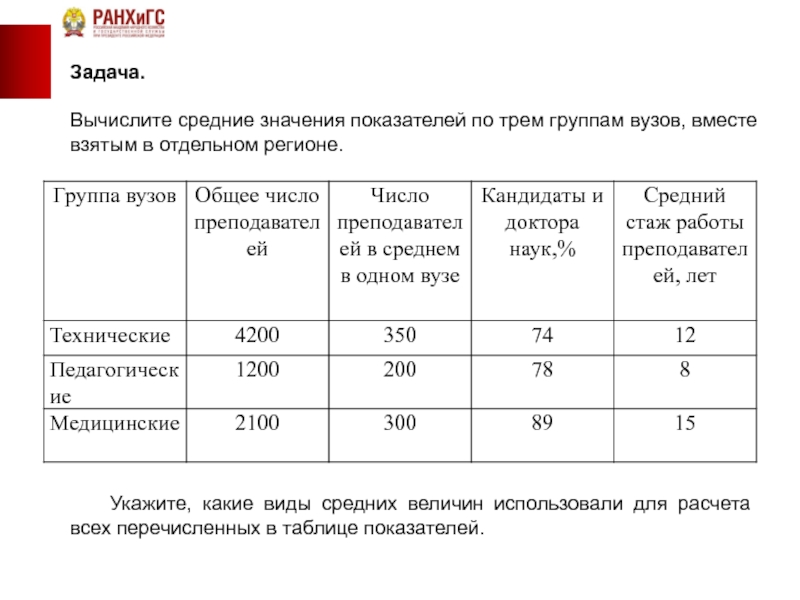
Вычислите средние значения показателей по трем группам вузов, вместе взятым
Укажите, какие виды средних величин использовали для расчета всех перечисленных в таблице показателей.
Слайд 29
Решение.
Поскольку нет информации о числе вузов каждой группы, т.е. частоты неизвестны,
Слайд 30
Средний процент кандидатов и докторов наук в расчете на один вуз
Средний стаж работы преподавателей также рассчитаем по средней арифметической взвешенной:
Слайд 31
Задача
Дан ряд чисел: 15; 15; 12; 14; 13. Найдите размах,
Решение
Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.
В данном случае размах равен R = 15-12 = 3
2) Среднее арифметическое данного ряда находим по формуле средней арифметической простой. Хср = (15+15+12+14+13)/5=13,8
3) Для определения медианы необходимо предложенный ряд упорядочить – расположить числа, например, в порядке возрастания: 12; 13; 14; 15; 15.
Медиана нечетного количества чисел в дискретном ряде – это число, записанное посередине. Медиана четного количества чисел – это среднее арифметическое двух чисел, находящихся посередине.
Поскольку в нашем случае количество чисел ряда нечетное, то Ме = 14.
4) Мода дискретного ряда чисел – это число, которое встречается в данном ряде чаще других. Так как число 15 встречается в нашем ряде чаще других, то Мо = 15.
Слайд 32
Задача
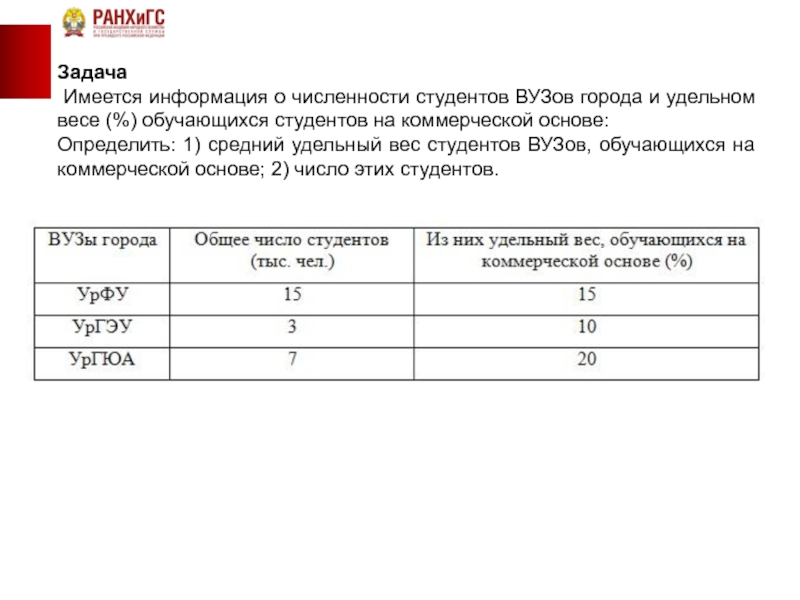
Имеется информация о численности студентов ВУЗов города и удельном
Определить: 1) средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе; 2) число этих студентов.
Слайд 33
Решение
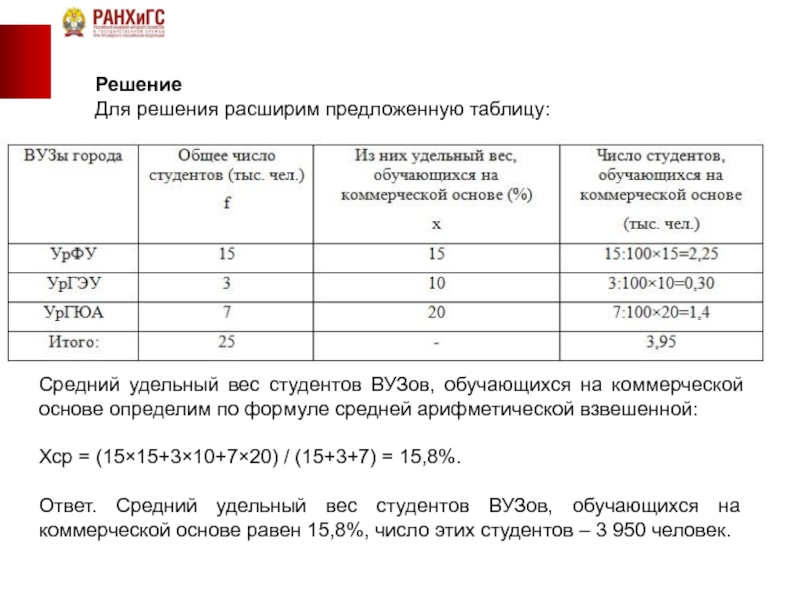
Для решения расширим предложенную таблицу:
Средний удельный вес студентов ВУЗов, обучающихся на
Хср = (15×15+3×10+7×20) / (15+3+7) = 15,8%.
Ответ. Средний удельный вес студентов ВУЗов, обучающихся на коммерческой основе равен 15,8%, число этих студентов – 3 950 человек.
Слайд 34
Задача.
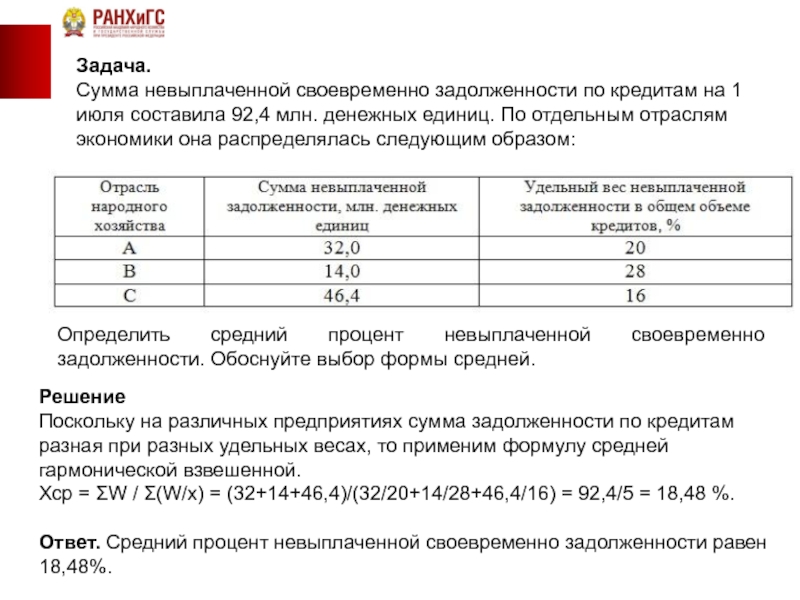
Сумма невыплаченной своевременно задолженности по кредитам на 1 июля составила
Определить средний процент невыплаченной своевременно задолженности. Обоснуйте выбор формы средней.
Решение
Поскольку на различных предприятиях сумма задолженности по кредитам разная при разных удельных весах, то применим формулу средней гармонической взвешенной.
Хср = ΣW / Σ(W/х) = (32+14+46,4)/(32/20+14/28+46,4/16) = 92,4/5 = 18,48 %.
Ответ. Средний процент невыплаченной своевременно задолженности равен 18,48%.
Слайд 35
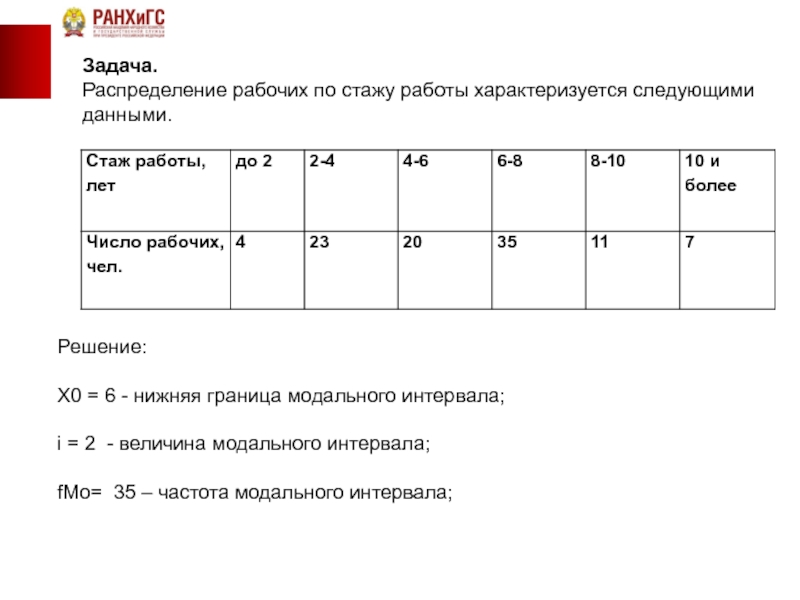
Задача.
Распределение рабочих по стажу работы характеризуется следующими данными.
Решение:
Х0 = 6 -
i = 2 - величина модального интервала;
fMo= 35 – частота модального интервала;
Слайд 36
fMo-1 = 20 - частота интервала соответственно предшествующего модальному
fMo+1 =
Определить моду интервального ряда распределения.
Мода интервального ряда составляет
Слайд 37
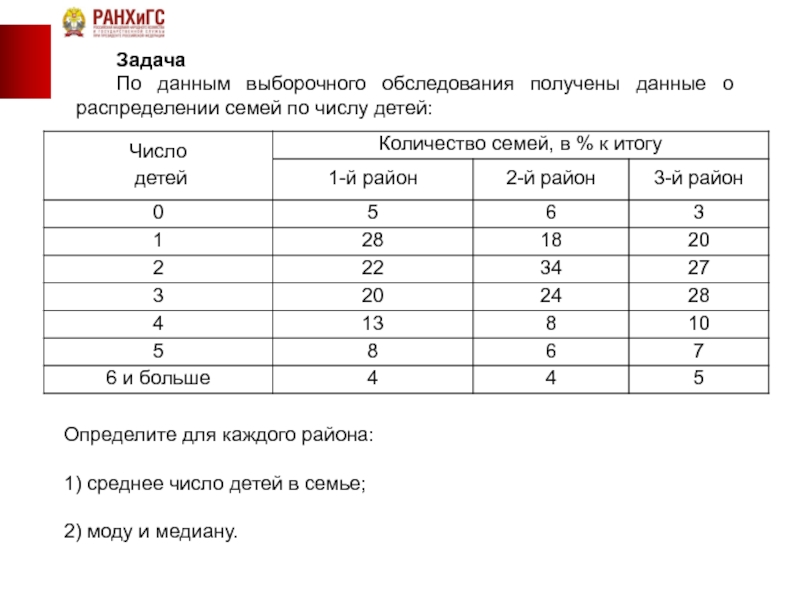
Задача
По данным выборочного обследования получены данные о распределении семей по числу
Определите для каждого района:
1) среднее число детей в семье;
2) моду и медиану.
Слайд 38
Решение:
Определим в каждом районе среднее число детей в семье, используя формулу
1-й район
2-й район
3-й район
Слайд 39
2) Определим для каждого района моду и медиану:
1-й район
Так как, мода
Следовательно, мода равна 1.
M0=1 ребенок
Для нахождения медианы:
а) проранжируем ряд: 4; 5; 8; 13; 20; 22; 28
б) найдем номер медианы
в) Me=13% - 4 детей
Слайд 40
2-й район
M0=2 детей
Найдем медиану:
а) 4; 6; 6; 8; 18; 24; 34
б)
в) Me=8% - 4 детей
3-й район
M0=3 детей
Найдем медиану:
а) 3; 5; 7; 10; 20; 27; 28
б) найдем номер медианы
в) Me=10% - 4 детей
Слайд 41
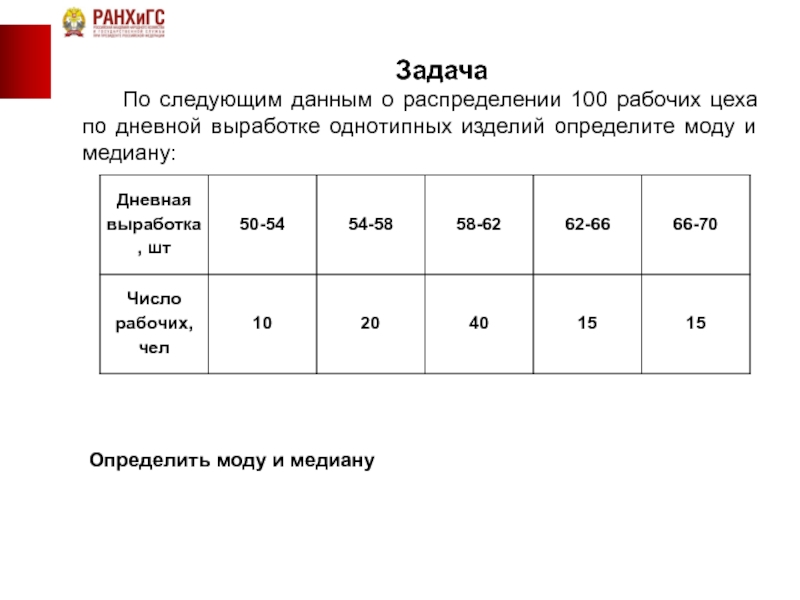
Задача
По следующим данным о распределении 100 рабочих цеха по дневной
Определить моду и медиану
Слайд 42
Определим медианный интервал. Им считается тот, до которого сумма накопленных частот
Итак, 50% рабочих вырабатывают в день меньше 60 изделий, а остальные 50% - более 60 шт.
Слайд 45
Коэффициент вариации
Из всех показателей вариации среднеквадратическое отклонение в наибольшей степени используется
Формула коэффициента вариации:
Данный показатель измеряется в процентах (если умножить на 100%).
В статистике принято, что, если коэффициент вариации
меньше 10%, то степень рассеивания данных считается незначительной,
от 10% до 20% - средней,
больше 20% и меньше или равно 33% - значительной,
значение коэффициента вариации не превышает 33%, то совокупность считается однородной,
если больше 33%, то – неоднородной.
Слайд 50
Экономические индексы в статистике
В статистике индексом называют показатель относительного изменения данного
Индексный метод направлен на решение следующих задач:
- характеристика общего изменения уровня сложного социально-экономического явления;
- анализ влияния каждого из факторов на изменение индексируемой величины путем элиминирования воздействия прочих факторов;
- анализ влияния структурных сдвигов на изменение индексируемой величины.
Слайд 51
Экономические индексы в статистике
Индивидуальный индекс (i) - характеризует изменение во времени
Индивидуальный индекс цены:
ip = p1/p0,
где p1 - цена товара в текущем периоде,
p0 - цена товара в базисном периоде;
Индивидуальный индекс физического объема реализации (количества товара):
iq = q1/q0,
где q1 – физический объем реализации товара в текущем периоде,
q0 – физический объем реализации товара в базисном периоде;
Слайд 52
Экономические индексы в статистике
Индивидуальный индекс товарооборота:
ipq = p1q1/p0q0;
Индивидуальный индекс себестоимости
iz=z1/z0
где z1 – себестоимость произведенной продукции в текущем периоде,
z0 – себестоимость произведенной продукции в базисном периоде.
Слайд 53
Экономические индексы в статистике
В тех случаях, когда исследуются не единичные объекты,
Слайд 55
Экономические индексы в статистике
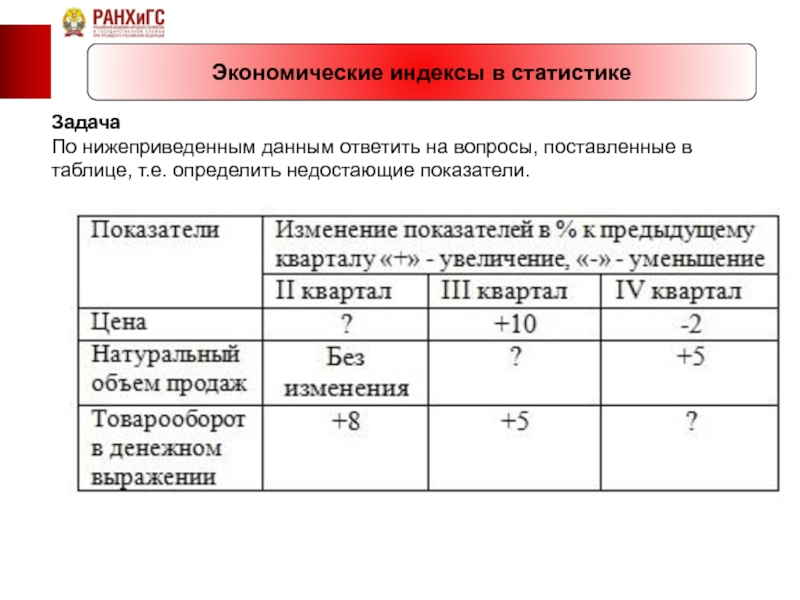
Задача
По нижеприведенным данным ответить на вопросы, поставленные
Слайд 56
Экономические индексы в статистике
Решение
1) ІІ квартал: Ip= ?; Iq= 1; Ipq
Ip = Ipq/Iq = 1,08:1 = 1,08 (в таблицу поместим +8).
2) ІІІ квартал: Ip = 1,1; Iq = ?; Ipq =1,05
Iq = Ipq/Ip = 1,05:1,1 = 0,95 (в таблицу поместим -5).
3) ІV квартал: Ip =0,98; Iq = 1,05; Ipq =?
Ipq = Ip×Iq = 0,98×1,05 = 1,029 ≈ 1,03 (в таблицу поместим +3).
Слайд 57
Экономические индексы в статистике
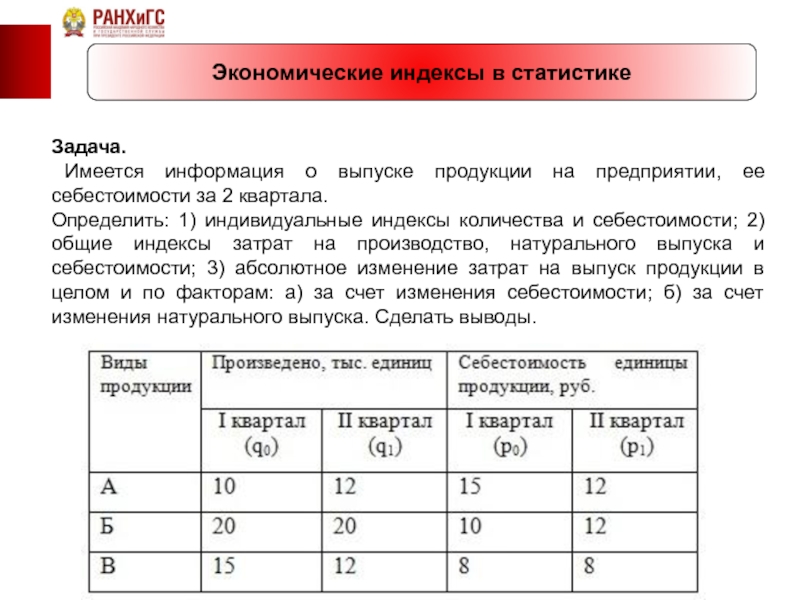
Задача.
Имеется информация о выпуске продукции на предприятии,
Определить: 1) индивидуальные индексы количества и себестоимости; 2) общие индексы затрат на производство, натурального выпуска и себестоимости; 3) абсолютное изменение затрат на выпуск продукции в целом и по факторам: а) за счет изменения себестоимости; б) за счет изменения натурального выпуска. Сделать выводы.
Слайд 58
Решение
1) Найдем индивидуальные индексы количества:
для продукции А: iq = q1/q0
для продукции Б: iq = q1/q0 = 20/20=1;
для продукции В: iq = q1/q0 = 12/15=0,8
Найдем индивидуальные индексы себестоимости:
для продукции А: iz = z1/z0 = 12/15=0,8;
для продукции Б: iz = z1/z0 = 12/10=1,2;
для продукции В: iz = z1/z0 = 8/8=1
2) общий индекс затрат на производство найдем по формуле:
(12*12+12*20+8*12)/(15*10+10*20+8*15) = 480/470 = 1,021=102,1%
Слайд 59
(12*15+20*10+12*8)/470 = 476/470 = 1,013 = 101,3%
Общий индекс натурального выпуска
Общий индекс
480/476 = 1,008=100,8%
Слайд 60
3) абсолютное изменение затрат на выпуск продукции в целом:
480-470=10 тыс.руб.
По факторам:
480-476=4 тыс.руб.
б) за счет изменения натурального выпуска
476-470 = 6 тыс.руб.
Вывод: Товарный выпуск во втором квартале увеличился по сравнению с первым на 102,1-100=2,1%. В абсолютном выражении это соответствует 10 тыс. руб. Этот рост произошел как за счет увеличения объема выпуска (на 101,3-100=1,3% или 6 тыс. руб.), так и за счет себестоимости (100,8-100=0,8% или 4 тыс. руб.).
Слайд 61
Экономические индексы в статистике
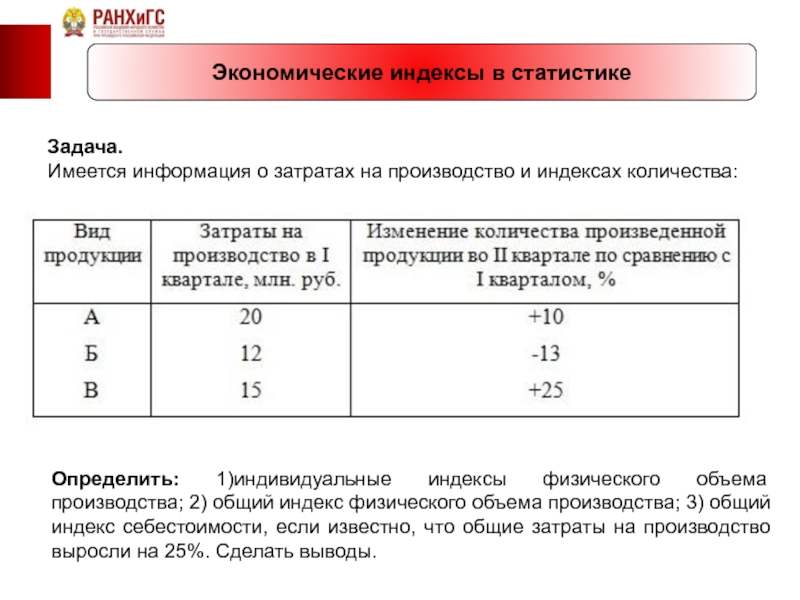
Задача.
Имеется информация о затратах на производство и индексах
Определить: 1)индивидуальные индексы физического объема производства; 2) общий индекс физического объема производства; 3) общий индекс себестоимости, если известно, что общие затраты на производство выросли на 25%. Сделать выводы.
Слайд 62
Решение
1) Найдем индивидуальные индексы количества:
для продукции А: iq = q1/q0
для продукции Б: iq = q1/q0 = (100-13)/100 = 87/100=0,87;
для продукции В: iq = q1/q0 = (100+25)/100 = 125/100=1,25
2) Поскольку известны затраты на производство в І квартале по каждому виду продукции (z0q0), где z0 - себестоимость продукции,
q0- количество произведенной продукции, то найдем:
для продукции А: z0q1= z0q0*iq = 20*1,1 = 22;
для продукции Б: z0q1= z0q0*iq = 12*0,87 = 10,44;
для продукции В: z0q1= z0q0*iq = 15*1,25 = 18,75
Далее найдем общий индекс объема производства:
Слайд 63
(22+10,44+18,75)/(20+12+15)=51,19/47=1,089=108,9%
3) Поскольку общие затраты на производство выросли на 25%, то общий
Найдем общий индекс себестоимости:
Iz = Izq:Iq = 1,25:1,089 = 1,148 =114,8%
Вывод: Увеличение общих затрат на производство во втором квартале на 25% произошло как за счет увеличения объема выпуска на 108,9-100=8,9%, так и за счет увеличения себестоимости на 114,8-100= 14,8%.
Слайд 64
Абсолютные и относительные величины в статистике.
Система статистических показателей - это совокупность
Исходной, первичной формой выражения статистических показателей являются абсолютные величины. Статистические показатели в форме абсолютных величин характеризуют абсолютные размеры изучаемых статистикой процессов и явлений, а именно, их массу, площадь, объем, протяженность, отражают их временные характеристики, а также могут представлять объем совокупности, т.е. число составляющих ее единиц.
Слайд 65
Абсолютные и относительные величины в статистике.
В зависимости от социально-экономической сущности исследуемых
Натуральные единицы измерения отражают естественные свойства явлений и измеряются в физических единицах меры веса, объема, протяженности и т.д.
Стоимостные единицы измерения отражают несоизмеримые в натуральном выражении процессы и представляют собой их денежное выражение.
К трудовым единицам измерения, позволяющим учитывать как общие затраты труда на предприятии, так и трудоемкость отдельных операций технологического процесса, относятся человеко-дни и человеко-часы.
Слайд 66
Абсолютные и относительные величины в статистике.
Относительный статистический показатель представляет собой результат
При расчете относительного показателя абсолютный показатель, находящийся в числителе получаемого отношения, называется текущим или сравниваемым. Показатель же, с которым производится сравнение и который находится в знаменателе, называется основанием или базой сравнения.
Относительные показатели могут выражаться в коэффициентах, процентах (%), промилле (‰).
Слайд 67
Все используемые на практике относительные статистические показатели можно подразделить на следующие
Относительные показатели динамики
Относительные показатели плана (плановое задание)
Относительные показатели реализации плана (выполнение плана)
Относительные показатели структуры – определяют удельные веса отдельных частей в целом, находят как отношение структурной части изучаемого объекта к его целому.
Относительные показатели координации - представляют собой отношение одной части совокупности к другой части этой же совокупности.
Относительные показатели интенсивности и уровня экономического развития - характеризуют степень распространения изучаемого процесса или явления, находят как отношение исследуемого показателя к размеру присущей ему среды.
Относительные показатели сравнения – находят как отношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.).
Слайд 68
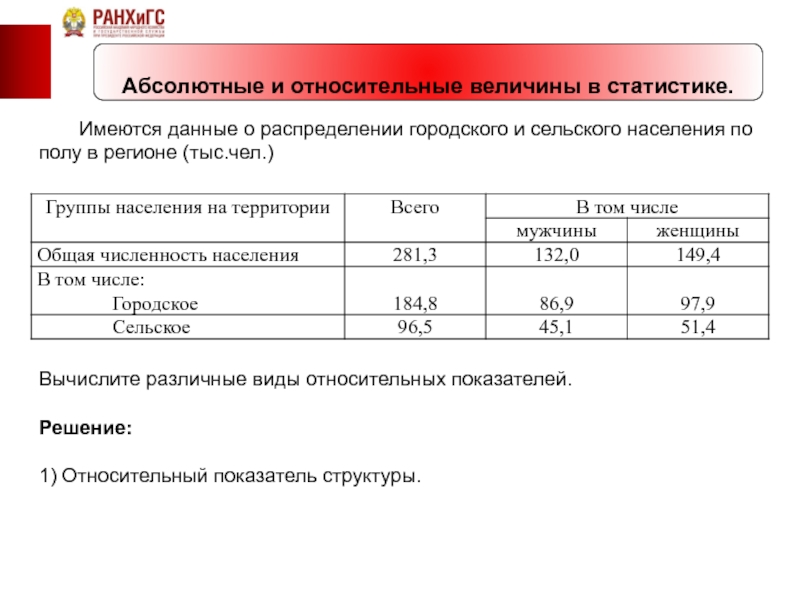
Абсолютные и относительные величины в статистике.
Имеются данные о распределении городского и
Вычислите различные виды относительных показателей.
Решение:
1) Относительный показатель структуры.
Слайд 69
Доля городского и сельского населения:
- доля городского населения
- доля сельского населения
Удельный
- доля мужчин.
- доля женщин.
Слайд 70
2) Относительный показатель координации:
Сколько жителей города приходится на 100 жителей села:
-
Сколько женщин приходится на 100 мужчин:
- женщин.