- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определители второго и третьего порядка. (Лекция 2) презентация
Содержание
- 1. Определители второго и третьего порядка. (Лекция 2)
- 2. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го
- 3. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го
- 4. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го
- 5. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го
- 6. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го
- 7. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го
- 8. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го
- 9. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
- 10. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Свойства определителя: 1. Определитель
- 11. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Свойства определителя: 5.Определитель изменит знак
- 12. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Примеры: Вычислить определитель: Р
- 13. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Примеры: Способ II (присоединение двух дополнительных строк):
- 14. ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ Примеры: П р и м
- 15. Компланарные векторы Определение. Три вектора
- 16. Ориентация тройки векторов Определение. Три некомпланарных вектора
- 17. Векторное произведение двух векторов Определение. Векторным произведением
- 18. Векторное произведение двух векторов
- 19. Основные свойства векторного произведения Теорема 1. Векторное
- 20. Основные свойства векторного произведения Теорема 4. Для
- 21. Выражение векторного произведение через прямоугольные координаты Пусть
- 22. Смешанное произведение трех векторов Пусть
- 23. Выражение смешанного произведения через прямоугольные координаты Пусть
- 24. Пример. Найти объем пирамиды с вершинами
Слайд 1Лекция 2
Определители второго и третьего порядка.
Векторное произведение двух векторов
Смешанное произведение трех
Слайд 2ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
О п р
(или |A|)
и вычисляемое по формуле:
(1)
Слайд 3ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
О п р е
(или |A|)
и вычисляемое по формуле:
(2)
Слайд 4ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
З а м е
1) Для вычисления определителя третьего порядка можно воспользоваться правилом разложения определителя по элементам л ю б о й строки (столбца) матрицы А.
При этом элементы выбранной строки (столбца) берут со знаками, указанными в следующей схеме:
то есть знак «+» ставят у тех элементов аij , для которых сумма индексов i+j есть число четное, «–» – сумма индексов i+j есть число нечетное.
Слайд 5ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
Например, выбрав для разложения
Слайд 6ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
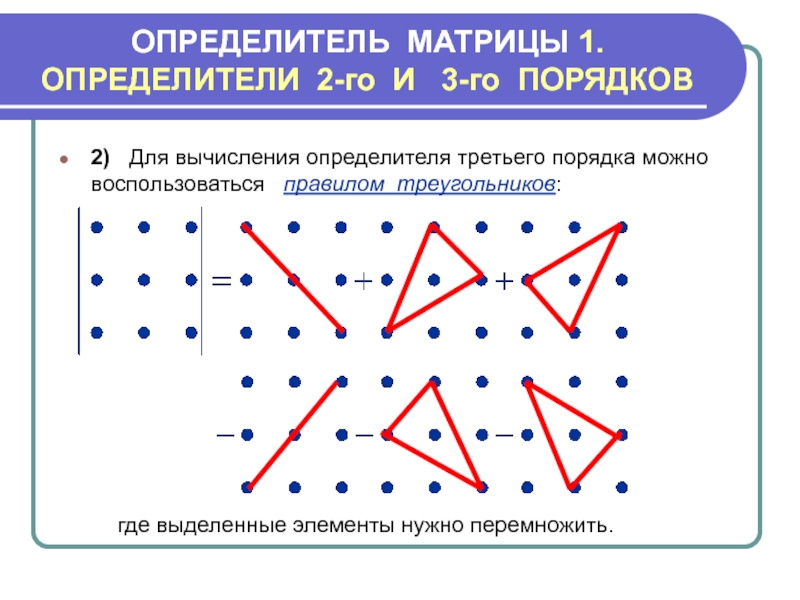
2) Для вычисления
где выделенные элементы нужно перемножить.
Слайд 7ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
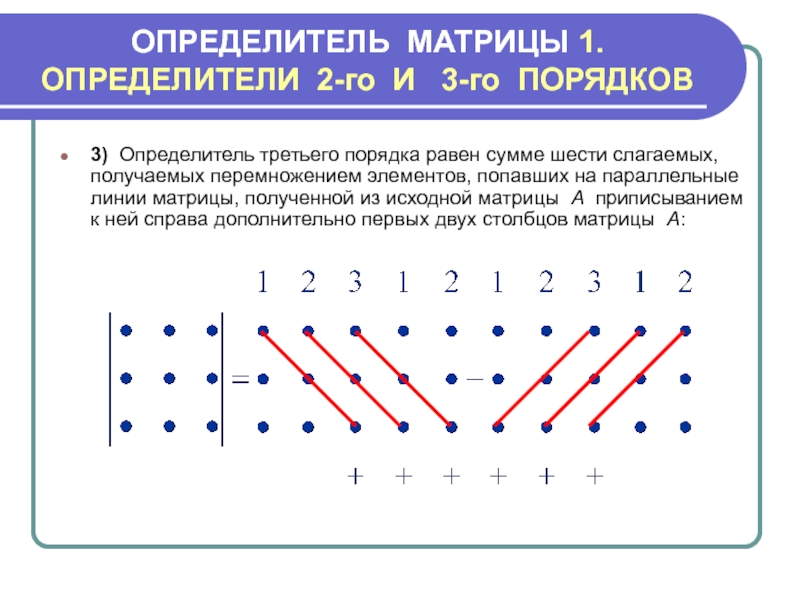
3) Определитель третьего порядка
Слайд 8ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1.ОПРЕДЕЛИТЕЛИ 2-го И 3-го ПОРЯДКОВ
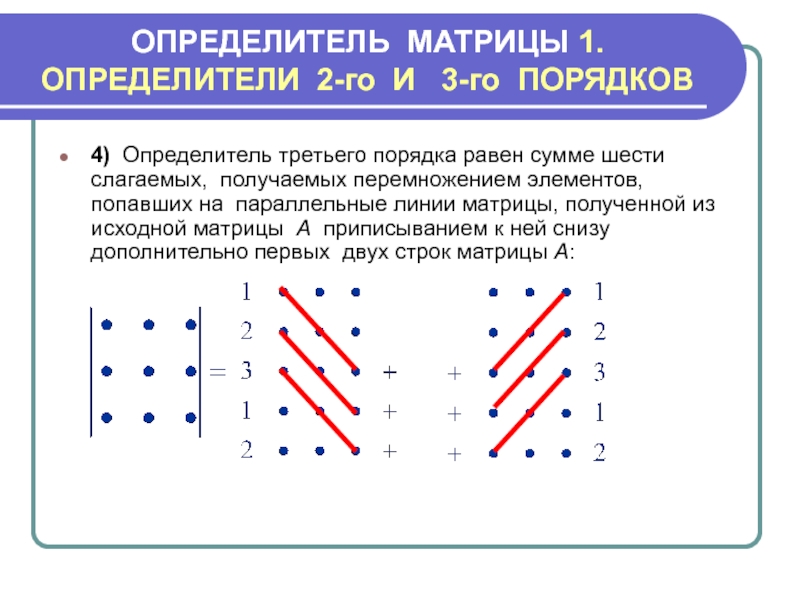
4) Определитель третьего порядка
Слайд 9ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
2. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
О п р е д
и так далее:
Слайд 10ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Свойства определителя:
1. Определитель не меняется при замене в нем
2. Определитель равен нулю, если содержит нулевую строку или нулевой столбец;
3. Определитель равен нулю, если содержит две одинаковые строки или два одинаковых столбца;
Слайд 11ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Свойства определителя:
5.Определитель изменит знак на противоположный, если в нем поменять
6.Определитель не изменится, если в нем заменить строку суммой этой строки и некоторой другой, вспомогательной, предварительно умноженной на какое-либо число (то есть применено элементарное преобразование второго типа);
7.Если строку (столбец) определителя умножить на некоторое число (то есть применено элементарное преобразование третьего типа), то определитель умножится на это число.
Слайд 12ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Примеры:
Вычислить определитель:
Р е ш е н и е.
Слайд 14ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Примеры:
П р и м е р . Вычислить определитель
Слайд 15Компланарные векторы
Определение. Три вектора
В противном случае векторы
называются некомпланарными .
Если хотя бы один
из векторов
нулевой, то эти векторы
компланарны.
Слайд 16Ориентация тройки векторов
Определение. Три некомпланарных вектора
кратчайший поворот от первого вектора ко второму вектору виден против часовой стрелки ( по часовой стрелке).
Ориентация тройки векторов
не меняется при циклической
перестановке этих векторов.
.
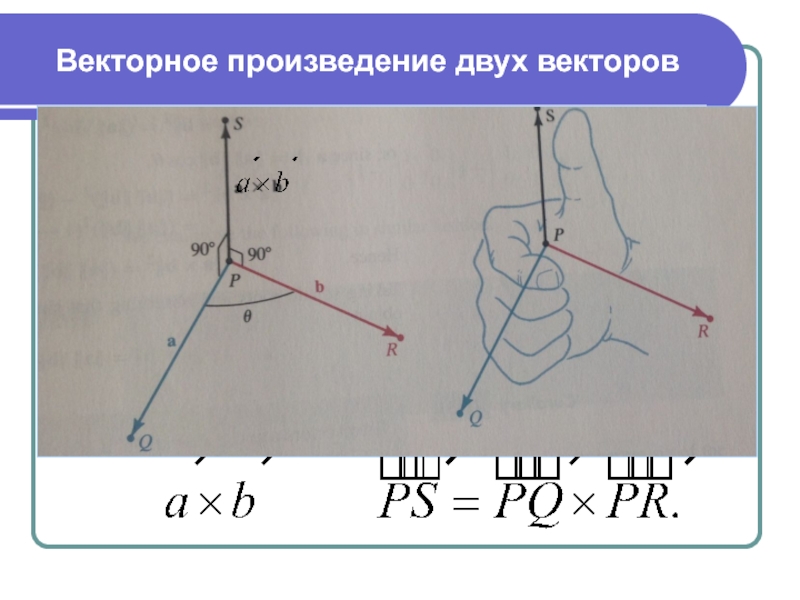
Слайд 17Векторное произведение двух векторов
Определение. Векторным произведением вектора
на вектор называется
условиям:
1. длина вектора равна
где угол между векторов и .
вектор ортогонален векторам и .
векторы образуют правую тройку.
Векторное произведение вектора на вектор
обозначается или .
Слайд 19Основные свойства векторного произведения
Теорема 1. Векторное произведение
Теорема 2. Длина вектора числено равна площади параллелограмма, сторонами которого служат векторы .
Теорема3. Векторное произведение антикоммутативно, т.е.
Слайд 20Основные свойства векторного произведения
Теорема 4. Для произвольных векторов
Слайд 21Выражение векторного произведение через прямоугольные координаты
Пусть Oxyz - прямоугольная система
координат,
Слайд 22Смешанное произведение трех векторов
Пусть -произвольные
Определение: Число называется смешанным произведением векторов и обозначается через
Теорема 1. Смешанное произведение векторов
равно нулю тогда и только тогда, когда эти векторы компланарны.
Теорема 2. Смешанное произведение трех некомпланарных векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если эти векторы образуют правую тройку, и со знаком «-», если они образуют левую тройку.
Слайд 23Выражение смешанного произведения через прямоугольные координаты
Пусть Oxyz –прямоугольная система координат в
Теорема. Пусть
Тогда
Следствие. Векторы
компланарны только и только тогда, когда
Слайд 24Пример. Найти объем пирамиды с вершинами
Решение. Данная пирамида построена на векторах
Вычислим смешанное произведение этих векторов по формуле
Ответ : 17
Смешанное произведение трех векторов